扩展功能
文章信息
- 黄远光, 朱锐, 张昌民, 瞿建华, 丁雲, 胡慧, 唐勇, 安志渊
- HUANG YuanGuang, ZHU RUI, ZHANG ChangMin, QU JianHua, DING Yun, HU Hui, TANG Yong, AN ZhiYuan
- 粗粒碎屑岩砾石定向性定量表征方法及应用
- A Method for Quantitative Characterization of Gravel Orientation and Its Application
- 沉积学报, 2018, 36(1): 12-19
- ACTA SEDIMENTOLOGICA SINCA, 2018, 36(1): 12-19
- 10.3969/j.issn.1000-0550.2018.004
-
文章历史
- 收稿日期:2017-02-15
- 收修改稿日期: 2017-04-25
2. 长江大学地球科学学院, 武汉 430100;
3. 中国石油新疆油田分公司, 新疆克拉玛依 834000
2. School of Geosciences, Yangtze University, Wuhan 430100, China;
3. PetroChina Xinjiang Oilfield Company, Karamay, Xinjiang 834000, China
非三维等轴砾石(尤其是扁平砾石)在流水或重力作用下,为了保持其最稳定的排列状态,会发生定向排列[1-3],如河流沉积中砾石叠瓦状构造。但在不同沉积条件下,砾石定向性特征会有所差异,定向性表征定量化是砾石定向性深入研究的必行途径,因为定量表征使定向性特征数值化,可以建立研究区砾石定向性特征数据库,使定向性特征和沉积物的其他属性(磨圆度、孔隙度等)特征精细比较和分析成为可能。Becker[4]对碎屑颗粒定向性进行了研究,将碎屑颗粒的优选排列称为叠瓦状构造。Richter[5]则采用直方图来表征冰碛物中鹅卵石的定向性特征。Wadell[6]提出科学采集砾石定向性数据的方法,并用极坐标图表征定向性特征。Holmes[7]运用星状图来表征冰碛物中扁长砾石的定向特征数据。Cailleux[8]依据扁长砾石的长轴方位角相对于平均方位角的差值将砾石定向性分为三个等级:定向性好、定向性一般、定向性差。Fisher[9]用等密度图表征砾石定向性,并总结了几个典型等密度图的形态模型以表征不同砾石定向性特征。Curray[10]运用向量思想,使砾石定向性表征由定性迈向了定量表征。Major[11]依据砾石长轴方位角分布集中程度将定向性等级划分为三个等级:定向性强、定向性弱、定向性差。Starkey[12]总结出8种定向性数据的分布模型:随机模式、十字形带状模式、小圆形带状相邻模式、对称双峰模式、带状模式、小型圆形条带模式、部分带状模式、密集单峰模式。Rust[13]运用定量方法对河流中砾石定向性特征做了研究,发现河流沉积中砾石定向性好。Lindsay[14]、Lawson[15]、Domack[16]运用等密度图对泥石流中砾石定向性特征做了研究,发现泥石流沉积中砾石定向性特征是差到中等。Spotts[17]运用定量方法对野外浊流沉积中颗粒定向性做了研究,发现浊流沉积中颗粒定向性很好。国内学者吴磊伯等[1-3]与武安斌[18]运用等密度图对河漫滩砾石定向性展开了研究,发现河流沉积中砾石定向性好,杨光[19]在岩芯照片上分析砾石定向性,以视倾角10°为步长,用任意相邻3个视倾角区间频数之和的最大值与测量总数的比值作为衡量定向性的标准。倪良田等[20]对甘肃敦煌现代边滩砂级颗粒叠瓦状构造做了研究。目前为止,砾石定向性研究大多基于野外露头观察,通过砾石定向性特征差异,来辨识不同的砾石原始沉积环境。但在油气田勘探中,沉积相和沉积环境的判定大多是基于岩芯资料的观察,那么从岩芯资料入手,如何表征岩芯中砾石定向性特征以及其在垂向上是否存在旋回?砾石定向性定量表征是否可以用于沉积相的划分?地下岩芯砾石定向性特征定量研究,关键在于准确获取定向性原始数据,最难的是获取砾石长轴真实方位角。本文在玛湖凹陷岩芯图像分析与测量的基础上,引入砾石长轴视倾角概念,提出在岩芯上定量分析砾石定向性特征的方法,由此建立了玛湖地区砾石定向性等级划分方案,尝试将砾石定向性分析用于单井沉积相分析。
1 砾石定向性的数据采集基于高清岩芯照片,应用Coreldraw软件测量砾石长轴的视倾角(图 1),比用量角器测量,其误差要小很多。为了方便处理测量数据,在测量砾石长轴视倾角时,统一规定以向左的水平射线(如图 1射线OA)方向为测量的起始位置,然后沿着O点(O点统一为扁长砾石左下端点)顺时针旋转直到与扁长砾石的长轴(如图 1射线OB)平行或者重合,测得∠AOB就是砾石长轴的视倾角。

|
| 图 1 砾石视倾角测量示意图 Figure 1 Gravel inclination angle measurement |
在岩芯图片上采集砾石长轴视倾角数据时,依据张昌民等[21]提出的岩石相划分方案,以岩石相为单位采集砾石定向性数据,在分析数据时,同样以岩石相为单位统计和分析样本砾石定向性特征。
2 砾石定向性数据统计及其定量表征砾石长轴视倾角数据采集完后,以10°大小为步长,统计每个样本中各个区间的砾石个数,得到每个样本中各视倾角区间的频数(Ni),再用每个区间的频数(Ni)占总频数(N)的比率即为每个视倾角区间的频率(Xi)(表 1)。
| 视倾角区间 | 0~10 | 10~20 | 20~30 | …… | 170~180 | N |
| 频数(Ni) | ||||||
| 频率%(Xi) |
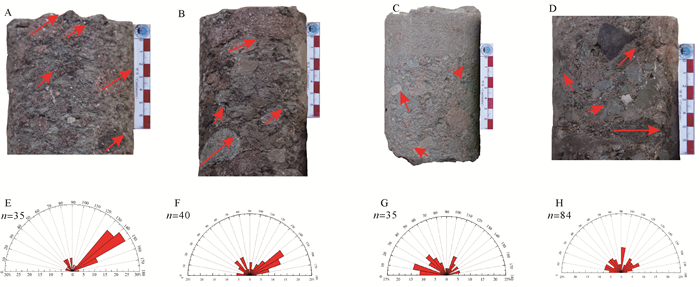
根据表 1统计结果,运用每个区间砾石长轴视倾角频率的大小绘制每个样本的砾石长轴视倾角玫瑰花图,玫瑰花图(图 2)中小扇形半径值越大、分布越集中,表示样本的砾石定向性越好。虽然玫瑰花图能够直观的表征砾石定向性特征,但是其不能准确的表征各样本之间差异性。因此需要引进数值来精确的表征砾石定向性,以精确区分各样本之间的差异,使砾石定向性研究由定性走向定量。
|
| 图 2 不同等级砾石定向性特征实例 A.有明显定向性,a=63.63%,σ=8.77,E为其相对应的玫瑰花图;B.有一定定向性,a=36.8%,σ=3.9,F为其相对应的玫瑰花图;C.有模糊定向性,a =28.6%,σ=4.1,G为其相对应的玫瑰花图;D.定向性杂乱,a =20.2%,σ=2.3,H为其相对应的玫瑰花图 Figure 2 Examples of different grading orientation characteristics |
参考杨光[19]在岩芯图片上研究砾石定向性的方法,引入统计参数a,(a为玫瑰花图中任意相邻三个小扇形半径之和的最大值)。依据砾石定向性的定义可知,参数a值越大则表明砾石定向性越好。由于a不能表征玫瑰花图中不同区间小扇形大小的差异性,所以仅依据参数a无法准确表征砾石长轴视倾角分布特征。例如,当a值相同时,只能保证三个小扇形半径之和最大值相同,却不能保证玫瑰花图中各扇形半径大小也相同。也就是说,当a值相同时,砾石定向性特征不一定相同。鉴于此,参考盛骤等[22]引入另一个统计参数方差σ(式1),其中X为玫瑰花图中小扇形半径大小的平均值,Xi为第i个角度区间中小扇形半径大小,参数σ用来描述玫瑰花图中小扇形大小与其平均值的偏离程度,其可以表征玫瑰花图中小扇形半径大小的差异。当σ值很大时,表明玫瑰花图中小扇形大小与其平均值的偏离程度很大,即玫瑰花图中小扇形半径的大小差异很大,砾石定向性较好(图 2A,2E);相反地,当σ很小时,表明玫瑰花图中小扇形大小与其平均值的偏离程度很小,即玫瑰花图中小扇形半径的大小差异不大,砾石定向性杂乱(图 2D,2H)。由此说明,σ值越大,砾石定向性越好;σ值越小,砾石定向性越差。如图 2所示实例中同样也反应出σ值能表征砾石定向性好坏。
 (1)
(1)
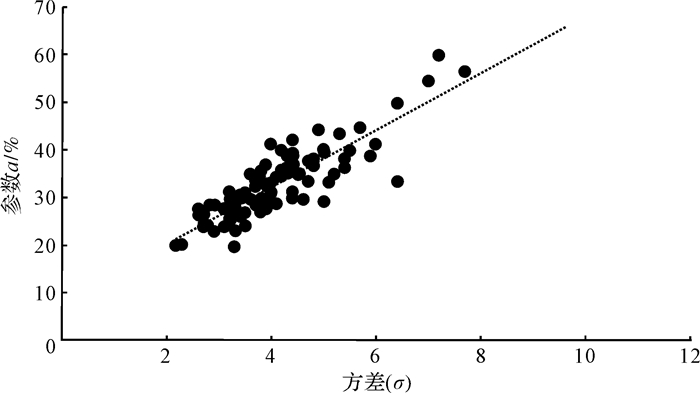
由上面分析发现参数a和σ都能表征砾石定向性,并且参数a和σ成正相关(图 3)。参数a和σ都能够表征砾石定向性,且参数σ能够弥补a的不足。因此考虑综合用参数a和σ表征砾石定向性,可更加准确的表征砾石定向性特征和不同样本间砾石定向性的差异。例如,当两个样本的a值相同时,可以再比较参数σ,σ值越大则表明定向性越好。
|
| 图 3 M152井参数a和σ散点分布图 Figure 3 The distribution parameters a and σ of Well M152 |
Holmes[7]、Sohn et al.[23]和Schluger[24]认为岩层中的砾石定向性可以用来解释沉积环境和沉积过程,匡立春等[25],唐勇等[26]认为玛湖地区百口泉组是一套砂砾质扇三角洲沉积体系,沉积了大套砾岩,沉积构造复杂,在岩芯上难以辨认,如果能够用砾石定向性辅助判断砾岩沉积构造,将会对砾岩的岩石相划分和沉积相研究有帮助。因此对玛湖地区砾石定向性定量表征和等级划分十分有必要,这将对该区的沉积相与沉积体系的研究提供有力的依据。
本文选取该区M152井取芯资料作为统计分析的对象,共选取95块岩芯样品(岩芯照片),并统计了每块岩芯中砾石的定向性统计参数a和σ(表 2)。由表 2可知,σ最大值为7.7,σ最小值为2.2,a最大值为60%,a最小值为19.7%,可见参数σ和a变化范围很大,参数a和σ对砾石定向性有很好的区分度,因此可以用参数σ和a来定量表征玛湖地区砾石定向性,并且参数σ和a的数值越大则砾石定向性越好。
| 样品编号 | 深度/m | σ | a /% | 定向性等级 | 岩石相 | 样品编号 | 深度/ m | σ | a/% | 定向性等级 | 岩石相 | |
| 1 | 3 093.43 | 3.30 | 19.70 | 定向性杂乱 | G3mtⅠ | 49 | 3 219.66 | 2.20 | 20.00 | 定向性杂乱 | G3mtⅠ | |
| 2 | 3 095.82 | 3.30 | 23.10 | 定向性杂乱 | G5mtⅠ | 50 | 3 219.87 | 3.90 | 36.80 | 有一定定向性 | G2xtⅠ | |
| 3 | 3 096.21 | 4.20 | 34.80 | 有模糊定向 | G4mtⅠ | 51 | 3 220.25 | 5.30 | 43.40 | 有明显定向性 | G4xtⅠ | |
| 4 | 3 096.71 | 3.40 | 26.00 | 定向性杂乱 | G4mggⅠ | 52 | 3 220.74 | 5.70 | 44.70 | 有明显定向性 | G4xtⅠ | |
| 5 | 3 097.06 | 3.20 | 30.00 | 定向性杂乱 | G5mtⅠ | 53 | 3 220.94 | 6.40 | 50.00 | 有明显定向性 | G4xggⅠ | |
| 6 | 3 097.42 | 2.60 | 26.20 | 定向性杂乱 | G4mggⅠ | 54 | 3 221.35 | 3.70 | 28.30 | 定向性杂乱 | G4mtⅠ | |
| 7 | 3 098.50 | 2.60 | 27.50 | 定向性杂乱 | G4mggⅠ | 55 | 3 221.69 | 5.00 | 29.20 | 有模糊定向性 | G3xtⅠ | |
| 8 | 3 109.10 | 3.80 | 35.50 | 有一定定向性 | G5xggⅢ | 56 | 3 222.24 | 5.00 | 40.10 | 有明显定向性 | G3xtⅠ | |
| 9 | 3 109.92 | 4.10 | 34.40 | 有模糊定向性 | G3pggⅢ | 57 | 3 222.49 | 4.00 | 30.60 | 有模糊定向性 | G3mtⅠ | |
| 10 | 3 123.71 | 2.70 | 26.40 | 定向性杂乱 | G4mtⅠ | 58 | 3 223.63 | 4.00 | 33.30 | 有模糊定向性 | G2mtⅠ | |
| 11 | 3 159.40 | 6.40 | 33.40 | 有模糊定向性 | G4mgbⅣ | 59 | 3 223.99 | 3.90 | 32.50 | 定向性杂乱 | G3mtⅠ | |
| 12 | 3 159.76 | 4.80 | 36.60 | 有明显定向性 | G5xgⅣ | 60 | 3 224.19 | 2.70 | 23.80 | 定向性杂乱 | G4mtⅠ | |
| 13 | 3 160.04 | 3.20 | 28.60 | 定向性杂乱 | G4mgbⅠ | 61 | 3 226.14 | 3.60 | 34.90 | 定向性杂乱 | G3mtⅠ | |
| 14 | 3 160.64 | 3.80 | 27.80 | 定向性杂乱 | G5mgbⅣ | 62 | 3 226.37 | 3.10 | 27.70 | 定向性杂乱 | G3mtⅠ | |
| 15 | 3 162.93 | 3.30 | 30.00 | 定向性杂乱 | G3mgbⅢ | 63 | 3 226.82 | 4.40 | 30.00 | 有模糊定向性 | G2mtⅠ | |
| 16 | 3 192.55 | 3.80 | 28.20 | 定向性杂乱 | G3mggⅠ | 64 | 3 226.96 | 4.30 | 39.20 | 有明显定向性 | G4xtⅠ | |
| 17 | 3 192.99 | 4.50 | 35.00 | 有明显定向性 | G3mtⅠ | 65 | 3 227.72 | 4.00 | 31.30 | 有模糊定向性 | G4mtⅠ | |
| 18 | 3 195.03 | 4.10 | 28.60 | 有模糊定向性 | G4mggⅠ | 66 | 3 228.03 | 4.10 | 28.90 | 有模糊定向性 | G5mtⅠ | |
| 19 | 3 196.79 | 5.90 | 38.90 | 有明显定向性 | G3xggⅠ | 67 | 3 229.36 | 4.40 | 38.50 | 有明显定向性 | G3xtⅠ | |
| 20 | 3 197.94 | 4.20 | 40.00 | 有明显定向性 | G3xggⅠ | 68 | 3 230.43 | 3.40 | 30.50 | 定向性杂乱 | G5mtⅠ | |
| 21 | 3 199.44 | 6.00 | 41.20 | 有明显定向性 | G4xtⅢ | 69 | 3 230.67 | 2.90 | 22.90 | 定向性杂乱 | G4mtⅢ | |
| 22 | 3 201.57 | 2.70 | 24.60 | 定向性杂乱 | G4mtⅠ | 70 | 3 231.77 | 7.20 | 60.00 | 有明显定向性 | G3xggⅢ | |
| 23 | 3 202.07 | 2.90 | 28.30 | 定向性杂乱 | G4mtⅠ | 71 | 3 232.16 | 4.70 | 37.80 | 有明显定向性 | G4xggⅢ | |
| 24 | 3 202.49 | 5.20 | 35.00 | 有明显定向性 | G3xtⅠ | 72 | 3 232.49 | 3.80 | 33.90 | 定向性杂乱 | G3mtⅠ | |
| 25 | 3 204.35 | 3.90 | 29.80 | 定向性杂乱 | G2mtⅠ | 73 | 3 233.75 | 3.70 | 33.30 | 定向性杂乱 | G2mtⅠ | |
| 26 | 3 204.77 | 4.00 | 29.40 | 有模糊定向性 | G2mtⅠ | 74 | 3 234.46 | 4.40 | 31.30 | 有模糊定向性 | G4mggⅠ | |
| 27 | 3 205.50 | 3.20 | 28.00 | 定向性杂乱 | G3mtⅠ | 75 | 3 234.99 | 3.10 | 24.10 | 定向性杂乱 | G4mggⅠ | |
| 28 | 3 205.65 | 3.60 | 29.60 | 定向性杂乱 | G3mtⅠ | 76 | 3 235.59 | 4.80 | 38.20 | 有明显定向性 | G3xtⅠ | |
| 29 | 3 206.11 | 5.10 | 33.30 | 有模糊定向性 | G3mggⅠ | 77 | 3 236.06 | 5.40 | 38.20 | 有明显定向性 | G5xtⅢ | |
| 30 | 3 206.24 | 3.20 | 31.30 | 定向性杂乱 | G3mggⅠ | 78 | 3 236.23 | 5.00 | 40.00 | 有明显定向性 | G4xtⅢ | |
| 31 | 3 207.53 | 4.20 | 35.30 | 有明显定向性 | G5xggⅠ | 79 | 3 236.63 | 2.80 | 28.40 | 定向性杂乱 | G3mtⅠ | |
| 32 | 3 207.70 | 4.40 | 42.20 | 有明显定向性 | G4xtⅠ | 80 | 3 237.91 | 3.30 | 27.10 | 定向性杂乱 | G3mtⅠ | |
| 33 | 3 207.92 | 2.30 | 20.20 | 定向性杂乱 | G2mtⅠ | 81 | 3 238.42 | 4.30 | 35.10 | 有明显定向性 | G3xtⅠ | |
| 34 | 3 208.50 | 5.50 | 40.00 | 有明显定向性 | G2ptⅠ | 82 | 3 238.72 | 3.70 | 32.20 | 定向性杂乱 | G3mtⅠ | |
| 35 | 3 209.79 | 4.70 | 33.30 | 有模糊定向性 | G3mtⅠ | 83 | 3 239.01 | 4.20 | 35.20 | 有明显定向性 | G5xtⅠ | |
| 36 | 3 209.99 | 4.00 | 41.20 | 有明显定向性 | G4mgⅠ | 84 | 3 239.44 | 4.30 | 36.50 | 有明显定向性 | G4xgbⅠ | |
| 37 | 3 210.37 | 4.60 | 29.70 | 有模糊定向性 | G4xtⅠ | 85 | 3 239.78 | 4.30 | 39.00 | 有明显定向性 | G3xtⅠ | |
| 38 | 3 210.59 | 5.40 | 36.40 | 有明显定向性 | G2mtⅠ | 86 | 3 241.53 | 4.40 | 36.90 | 有明显定向性 | G4xtⅠ | |
| 39 | 3 210.97 | 3.50 | 24.30 | 定向性杂乱 | G3mggⅠ | 87 | 3 244.64 | 2.70 | 26.90 | 定向性杂乱 | G3mggⅢ | |
| 40 | 3 211.97 | 4.10 | 28.80 | 有模糊定向性 | G5mrⅠ | 88 | 3 245.14 | 3.20 | 25.40 | 定向性杂乱 | G3mtⅢ | |
| 41 | 3 213.41 | 3.30 | 28.10 | 定向性杂乱 | G3mtⅠ | 89 | 3 248.74 | 5.00 | 39.50 | 有明显定向性 | G3xggⅠ | |
| 42 | 3 213.75 | 3.80 | 29.50 | 定向性杂乱 | G2mtⅠ | 90 | 3 249.63 | 3.80 | 26.80 | 定向性杂乱 | G5mtⅢ | |
| 43 | 3 214.72 | 4.20 | 35.80 | 有明显定向性 | G2ptⅠ | 91 | 3 252.45 | 3.50 | 30.90 | 定向性杂乱 | G5mggⅠ | |
| 44 | 3 215.12 | 7.70 | 56.50 | 有明显定向性 | G5xggⅢ | 92 | 3 255.43 | 3.40 | 29.60 | 定向性杂乱 | G4mtⅠ | |
| 45 | 3 215.32 | 3.50 | 26.80 | 定向性杂乱 | G3mggⅠ | 93 | 3 257.04 | 2.80 | 23.90 | 定向性杂乱 | G2mgⅢ | |
| 46 | 3 215.46 | 3.90 | 27.60 | 定向性杂乱 | G3mggⅠ | 94 | 3 258.28 | 4.40 | 39.40 | 有明显定向性 | G2xggⅠ | |
| 47 | 3 215.86 | 4.90 | 44.20 | 有明显定向性 | G4xgbⅠ | 95 | 3 259.14 | 4.20 | 35.30 | 有明显定向性 | G4xtⅠ | |
| 48 | 3 217.41 | 7.00 | 54.50 | 有明显定向性 | G5xgbⅠ | |||||||
| 注:岩石相命名据张昌民等(2016) | ||||||||||||
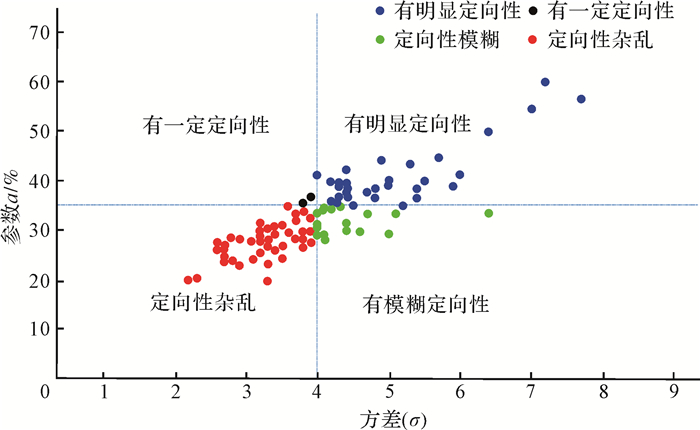
国内学者杨光[19]在利用岩芯图像分析砾石定向性时,其依据参数a将砾石定向性划分为有定向性和定向性杂乱,前文提到仅依据参数a来表征砾石定向性特征不够准确,同理仅依据参数a划分砾石定向性等级也不够准确。笔者在前人的研究基础上,结合玫瑰花图和岩芯照片并依据参数a和σ,提出了适用于玛湖地区砾石定向性等级划分方案(表 3),将砾石定向性等级划分为四个等级:有明显定向性、有一定定向性、有模糊定向性、定向性杂乱。即当a大于35%且σ大于4时,砾石定向性等级为有明显定向性;当a大于35%且σ小于4时,砾石定向性等级为有一定定向性;当a小于35%且σ大于4时,砾石定向性等级为有模糊定向性;当a小于35%且σ小于4时,砾石定向性等级为定向性杂乱。
| σ>4 | σ < 4 | |
| a>35% | 有明显定向性 | 有一定定向性 |
| a < 35% | 有模糊定向性 | 定向性杂乱 |
依据表 3的划分方案,将样品的定向性等级结果以及所对应的岩石相列举在表 2,由表 2可知,砾石定向性等级和砾岩岩石相有一定的关系,岩石相中包般较好,为有明显定向性和有一定定向性;岩石相中包含属性为块状层理(m)的,砾石定向性一般较差,定向性等级为有模糊定向性和定向性杂乱;砾石定向性在垂向上有一定的旋回性,例如从样品23~13,从下到上样品深度逐渐变小,定向性由差变好再变差,在样品21处,定向性最好,岩石相为G4xtⅢ,σ值为6,a值为42.2%,定向性等级为有明显定向性;在样品14处,砾石定向性最差,岩石相为G5mgbⅣ,σ值为3.8,a值为27.8,定向性等级为定向性杂乱。
依据唐勇等[26],于兴河等[27],邹志文等[28]对玛湖地区百口泉组沉积体系研究,玛152井取芯段属于三角洲前缘水下分流河道沉积,沉积水动力以牵引流沉积为主。依据Well[29],Todd[30],Schlee[31],Rust[32],Kauffman et al.[33]研究可知,在牵引流条件下(河流沉积、浊流沉积)砾石具有较好的定向性,在非牵引流环境(泥石流)中,砾石定向性比较差。因此玛152井取芯段的砾石定向性应较好。本文依据上述砾石定向性等级划分方案,对M152井的95块样品做了统计(图 4),砾石定向性杂乱所占的比例为45.2%,小于50%,说明M152井取芯段砾石定向性总体上比较好,也进一步说明对该区砾石定量表征的结果与沉积相研究具有一致性。因此,砾石定向性定量表征方法可以用于判断沉积水动力条件,为沉积相研究提供依据。
|
| 图 4 M152井砾石定向性等级图 Figure 4 Gravel orientation grading of M152 |
玛湖凹陷位于准噶尔盆地西北缘,是准噶尔盆地6大生烃凹陷之一,凹陷及其周缘是盆地最有利的油气成藏区。玛湖凹陷斜坡区地层发育较全,二叠纪至侏罗纪早期,玛湖凹陷一直是盆地的沉降中心之一,沉积了巨厚的陆源碎屑岩。本次研究目的层位为三叠系百口泉组百二段,为一套近源沉积的砂砾岩为主的沉积体。唐勇等[26]认为玛湖凹陷百口泉组地层发育扇三角洲群,FN16井位于准噶尔盆地玛湖凹陷夏子街扇左下边缘,取样部位(2 771.4~2 768.3 m)位于百二段上部,该次取芯的岩性主要为大中砾岩和小中砾岩;沉积构造主要以交错层理和块状层理为主;岩石颜色为灰绿色和灰色;支撑方式主要以颗粒支撑和多级颗粒支撑为主,岩石相类型:G4xggⅠ、G3mggⅠ、G4xgⅡ、G5xgⅡ、G5xgⅠ、G2xgⅠ、G3mggⅠ、G3mgⅠ。
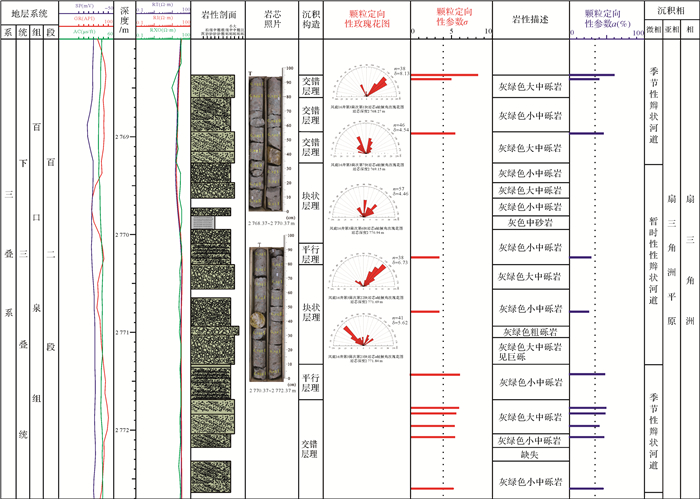
本次研究在该次取芯上选取了11个取样点,对11个样品的砾石定向性做了定量研究,计算出了样品的定向性参数a和σ的数值,依据取样点的深度,将定向性参数数值用杆状图表示在岩性柱状图上(图 5),方便其在沉积相分析中的应用。由图可知,参数σ最大值为8.13,最小值为4.37,11个样品中σ值都大于4;参数a最大值为65.79%,最小值为27.56%,依据本文提出的定向性等级划分方案可知该段砾石定向性等级主要以有明显定向性和有模糊定向性为主,由下到上,σ和a先变小再增大,在2 770.7 m处σ和a值最小。参考岩芯观察的沉积构造,定向性参数杆状图以及测井曲线的变化,可以将该段划分为三段,沉积微相主要为季节性辫状河道和暂时性辫状河道。季节性辫状河河道在一年内发生多次不规则的干涸,具有常年流水但流量随季节和天气变化极大,流水占有率较高,水流以暴雨和周期性的湿气流降水为主,砾石磨圆度高,砾石定向性好;暂时性河流在一年里基本都是干涸的,只有暴雨形成的微弱径流偶尔流过,以暴雨输入为主,常伴有泥石流,砾石磨圆度低,砾石定向性较差[34]。下面将分段来详细阐述研究层位的沉积特征。
|
| 图 5 FN16井定向性特征 Figure 5 Orientation characteristics of Well FN16 |
第一段起始深度为2 772.7~2 771.4 m,该段主要为灰绿色的大中砾岩和小中砾岩,沉积构造主要为交错层理,测井曲线为箱形,定向性参数比较大,a值为40%~60%,大于35%;σ数值为4.8~8.13,大于4,该段取的样品中砾石定向性较好,砾石定向性等级为有明显定向性,沉积时水动力比较稳定,以牵引流为主,综合考虑该段的沉积微相为季节性辫状河道。第二段的起始深度为2 771.4~2 770.1 m,该段岩性主要为灰绿色的大中砾岩和小中砾岩,测井曲线为齿化的箱型,沉积构造主要以块状层理为主,定向性参数σ值比较小,小于4,参数a值也比较小,小于35%,该段取样点的砾石定向性较差,砾石定向性等级为有模糊定向性,在沉积时水动力不稳定,综合考虑该段的沉积微相为暂时性辫状河道。第三段的起始深度为2 769.3~2 768.3 m,该段岩性主要为灰绿色的大中砾岩和小中砾岩,测井曲线以箱形和钟形为主,沉积构造主要以交错层理为主,在该段的取样点中,定向性参数数值较大,其中a值为40%~50%,大于35%;σ数值为4.76~8.2,大于4,该段定向性较好,砾石定向性等级为有明显定向性,沉积时水动力比较稳定,以牵引流为主,综合考虑该段岩芯的沉积微相划分为季节性辫状河道沉积。
由以上分析可知,在沉积相分析中,引入定向性参数,可以将沉积相划分的更加精细,而且定向性参数和沉积标志相互印证,从而使沉积相分析结果更加可靠。
5 结论(1) 在岩芯照片基础上,运用统计学的方法,引进参数a和σ在岩芯上定量表征砾石的定向性特征,其中a为玫瑰花图中任意相邻三个小扇形的半径之和的最大值,σ为玫瑰花图中小扇形大小与其平均值的偏离程度,经分析参数a和σ值越大,砾石定向性越好。
(2) 通过对M152井岩芯中砾石定向性的系统研究,发现可以依据参数a和σ将砾石定向性等级划分为四个等级:有明显定向性(a大于35%且σ大于4)、有一定定向性(a大于35%且σ小于4)、有模糊定向性(a小于35%且σ大于4)、定向性杂乱(a小于35%且σ小于4)。砾石定向性等级和岩石相有一定的关系,岩石相中包含属性为交错层理和平行层理的,定向性等级为有明显定向性和有一定定向性的;岩石相中包含属性为块状层理的,砾石定向性一般较差,定向性等级为有模糊定向性和定向性杂乱。
(3) 以FN16井第3次取芯为例,依据定向性参数大小、岩性特征、测井曲线以及沉积构造,将该次取芯分为三段,从下到上依次为季节性辫状河道、暂时性辫状河道、季节性辫状河道。季节性辫状河道中σ数值为4.8~8.13,a值为40%~62%,而暂时性辫状河道中σ数值小于4,参数a数值小于35%。
符号注释:
岩性:G5—细砾岩,G4—小中砾岩,G3—大中砾岩,G2—粗砾岩,G1—巨砾岩;
层理:m—块状层理,p—平行层理,x—交错层理;
颜色:gg—灰绿色,g—灰色,a—灰白色,t—灰褐色,r—红褐色系;
支撑方式:Ⅰ—颗粒支撑,Ⅱ—多级颗粒支撑,Ⅲ—杂基—颗粒支撑,Ⅳ—杂基支撑。
| [1] | 吴磊伯. 砾石定向测量的意义与方法[J]. 地质知识, 1957(12): 1-6. [ Wu Leibo. The significance and method of gravel orientation measurement[J]. Geological Knowledge, 1957(12): 1–6. ] |
| [2] | 吴磊伯, 马胜云, 沈淑敏. 砾石排列方位的分析并论述长沙等地白沙井砾石层的沉积构造[J]. 地质学报, 1958 (2): 201-231. [ Wu Leibo, Ma Shengyun, Shen Shumin. Gravel arrangement and analysis of the sedimentary structure of the Baisha mud gravel layer in Changsha and other places[J]. Acta Geologica Sinica, 1958(2): 201-231. ] |
| [3] | 吴磊伯, 沈淑敏. 海滨砾石组构分析的一个实例[J]. 地质学报, 1962, 42 (4): 353–361. [ Wu Leibo, Shen Shumin. An example of fabric analysis of seaside gravel[J]. Acta Geologica Sinica, 1962, 42(4): 353–361. ] |
| [4] | Becker G F. Finite homogeneous strain, flow and rupture of rocks[J]. Geological Society of America Bulletin, 1892, 4(1): 13–90. DOI: 10.1130/GSAB-4-13 |
| [5] | Richter K. Die Bewegungsrichtung des Inlandeises, rekonstruiert aus den Kritzen und Längsachsen der Geschiebe[J]. Z Geschiebeforsch, 1932, 8(1): 62–66. |
| [6] | Wadell H. Volume, shape, and shape position of rock fragments in openwork gravel[J]. Geografiska Annaler, 1936, 18: 74–92. |
| [7] | Holmes C D. Till fabric[J]. Geological Society of America Bulletin, 1941, 52(9): 1299–1354. DOI: 10.1130/GSAB-52-1299 |
| [8] | De Cailleux A. La Disposition Individuelle des Galets Dans les Formations Detritiques[M]. Paris: Société de Géographie Physique, 1938: 171-198. |
| [9] | Fisher R. Dispersion on a sphere[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1953, 217(1130): 295–305. DOI: 10.1098/rspa.1953.0064 |
| [10] | Curray J R. The analysis of two-dimensional orientation data[J]. The Journal of Geology, 1956, 64(2): 117–131. DOI: 10.1086/626329 |
| [11] | Major J J. Pebble orientation on large, experimental debris-flow deposits[J]. Sedimentary Geology, 1998, 117(3/4): 151–164. |
| [12] | Starkey J. The analysis of three-dimensional orientation data[J]. Canadian Journal of Earth Sciences, 1993, 30(7): 1355–1362. DOI: 10.1139/e93-116 |
| [13] | Rust B R. Pebble orientation in fluvial sediments[J]. Journal of Sedimentary Research, 1972, 42(2): 384–388. |
| [14] | Lindsay J F. The development of clast fabric in mudflows[J]. Journal of Sedimentary Research, 1968, 38(4): 1242–1253. |
| [15] | Lawson D E. A comparison of the pebble orientations in ice and deposits of the Matanuska Glacier, Alaska[J]. The Journal of Geology, 1979, 87(6): 629–645. DOI: 10.1086/628457 |
| [16] | Domack E W. Sedimentology of glacial and glacial marine deposits on the George V-Adelie continental shelf, East Antarctica[J]. Boreas, 1982, 11(1): 79–97. |
| [17] | Spotts J H. Grain orientation and imbrication in Miocene turbidity current sandstones, California[J]. Journal of Sedimentary Research, 1964, 34(2): 229–253. |
| [18] | 武安斌. 兰州许家滩-雁滩河漫滩砾石的沉积组构分析[J]. 兰州大学学报(自然科学版), 1977 (3): 119–125. [ Wu Anbin. Sedimentary organization analysis of gravel in Xujiatan-Yantan River floodplain in Lanzhou[J]. Journal of Lanzhou University (Natural Science Edition), 1977(3): 119–125. ] |
| [19] | 杨光. 岩心图像砾石分析技术在砂砾岩扇体中的应用:以东营凹陷北部陡坡带砂砾岩扇体为例[J]. 油气地质与采收率, 2010, 17 (5): 20–23. [ Yang Guang. Analytical technique of gravels in core image and its application in research of conglomerate fan-taking the conglomerate fan, northern steep slope, Dongying sag as an example[J]. Oil and Gas Geology and Recovery, 2010, 17(5): 20–23. ] |
| [20] | 倪良田, 钟建华, 李勇, 等. 甘肃敦煌现代边滩砂级颗粒叠瓦构造研究[J]. 沉积学报, 2016, 34 (2): 207–221. [ Ni Liangtian, Zhong Jianhua, Li Yong, et al. Study on the imbrication of sand-scale particles in modern point bar in Dunhuang city, Gansu[J]. Acta Sedimentologica Sinica, 2016, 34(2): 207–221. ] |
| [21] | 张昌民, 王绪龙, 朱锐, 等. 准噶尔盆地玛湖凹陷百口泉组岩石相划分[J]. 新疆石油地质, 2016, 37 (5): 606–614. [ Zhang Changmin, Wang Xulong, Zhu Rui, et al. Litho-facies classification of Baikouquan Formation in Mahu sag Junggar Basin[J]. Xinjiang Petroleum Geology, 2016, 37(5): 606–614. ] |
| [22] | 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 4版. 北京: 高等教育出版社, 2008. [ Sheng Zhou, Xie Shiqian, Pan Chengyi. Probability theory and mathematical statistics[M]. 4th ed. Beijing: Higher Education Press, 2008. ] |
| [23] | Sohn Y K, Kim S B, Hwang I G, et al. Characteristics and depositional processes of large-scale gravelly Gilbert-type foresets in the Miocene Doumsan fan delta, Pohang Basin, SE Korea[J]. Journal of Sedimentary Research, 1997, 67(1): 130–141. |
| [24] | Schluger P R. Depositional environments as interpreted from primary sedimentary structures and stratification sequences[J]. Geoscience Canada, 1975, 2(4): 297–305. |
| [25] | 匡立春, 唐勇, 雷德文, 等. 准噶尔盆地玛湖凹陷斜坡区三叠系百口泉组扇控大面积岩性油藏勘探实践[J]. 中国石油勘探, 2014, 19 (6): 14–23. [ Kuang Lichun, Tang Yong, Lei Dewen, et al. Exploration of fan-controlled large-area lithologic oil reservoirs of Triassic Baikouquan Formation in slope zone of Mahu depression in Junggar Basin[J]. China Petroleum Exploration, 2014, 19(6): 14–23. ] |
| [26] | 唐勇, 徐洋, 瞿建华, 等. 玛湖凹陷百口泉组扇三角洲群特征及分布[J]. 新疆石油地质, 2014, 35 (6): 628–635. [ Tang Yong, Xu Yang, Qu Jianhua, et al. Fan-delta group characteristics and its distribution of the Triassic Baikouquan reservoirs in Mahu sag of Junggar Basin[J]. Xinjiang Petroleum Geology, 2014, 35(6): 628–635. ] |
| [27] | 于兴河, 瞿建华, 谭程鹏, 等. 玛湖凹陷百口泉组扇三角洲砾岩岩相及成因模式[J]. 新疆石油地质, 2014, 35 (6): 619–627. [ Yu Xinghe, Qu Jianhua, Tan Chengpeng, et al. Conglomerate lithofacies and origin models of fan deltas of Baikouquan Formation in Mahu sag, Junggar Basin[J]. Xinjiang Petroleum Geology, 2014, 35(6): 619–627. ] |
| [28] | 邹志文, 李辉, 徐洋, 等. 准噶尔盆地玛湖凹陷下三叠统百口泉组扇三角洲沉积特征[J]. 地质科技情报, 2015, 34 (2): 20–26. [ Zhou Zhiwen, Li hui, Xu Yang, et al. Sedimentary characteristics of the Baikouquan Formation, lower Triassic in the Mahu depression, Junggar Basin[J]. Geological Science and Technology Information, 2015, 34(2): 20–26. ] |
| [29] | Wells N A. Sheet debris flow and sheetflood conglomerates in Cretaceous cool-maritime alluvial Fans, South Orkney Islands, Antarctica[J]. Cspg Special Publications, 1984: 133–145. |
| [30] | Todd S P. Process deduction from fluvial sedimentary structures[M]//Carling P A, Dawson M R. Advances in Fluvial Dynamics and Stratigraphy. New York: John Wiley & Sons Ltd, 1996: 299-350. |
| [31] | Schlee J. Fluvial gravel fabric[J]. Journal of Sedimentary Research, 1957, 27(2): 162–176. |
| [32] | Rust B R. Structure and process in a braided river[J]. Sedimentology, 1972, 18(3/4): 221–245. |
| [33] | Kauffman M E, Ritter D F. Cobble imbrication as a sensitive indicator of subtle local changes in river flow direction[J]. Geology, 1981, 9(7): 299–302. DOI: 10.1130/0091-7613(1981)9<299:CIAASI>2.0.CO;2 |
| [34] | Fryirs K A, Brierley G J. Geomorphic Analysis of River Systems:An Approach to Reading the Landscape[M]. Hoboken, NJ: John Wiley and Sons, 2012. |
 2018, Vol. 36
2018, Vol. 36


