| 高低双棱镜三角高程测量方法及精度分析 |
2. 武汉大学测绘学院,湖北 武汉,430079;
3. 天津市第九中学,天津,300000
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. The No.3 Middle School of Tianjin, Tianjin 300000, China
目前,高程测量无论是在国家基础设施建设还是在工程方面都占据着重要的地位。但是由于受到地球曲率、大气折光、仪器量测等多种误差因素的影响,精度不高。本文通过分析三角高程测量中误差产生的原因,提出一种能有效消除误差的方法,以提高三角高程测量的精度。
三角高程测量的精度受许多因素的影响, 归纳起来主要有以下几个方面[1]:①垂直角测角误差。垂直角测角误差对三角高程测量的影响与推算高差的边长有关,边长愈长,影响愈大; ②边长误差。边长误差与测距方法有关; ③大气折光误差。大气折光系数f在中午时最小,且比较稳定,日出和日落时稍大一些,且变化较大; ④仪器高、觇标高的量测误差。
针对上述误差源,提出了免仪器高、目标高同时对向三角高程观测法。
1 免仪器高、目标高同时对向三角高程观测法(高低双棱镜)原理免仪器高、目标高同时对向三角高程观测法(高低双棱镜)的原理如图 1所示。
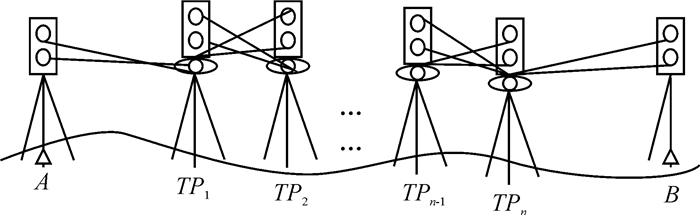 |
| 图 1 免仪器高、目标高对向三角高程观测法 Figure 1 Free of Instruments, Higher Goals to the Triangle Elevation Method |
1)在A、B两点间选n(n为偶数)个临时点作为转点, 点与点间要能互相通视。先在起始点A摆上棱镜, 在点TP1摆上全站仪, 对点A高低棱镜分别进行高差测量, 求得hA-TP1、h′A-TP1。
2)把另一台全站仪放到点TP2, 并在点TP2全站仪上放上棱镜,用点TP1上的全站仪对点TP2的高低棱镜进行高差测量, 求得hTP1-TP2、h′TP1-TP2, 同时用点TP2上的全站仪对点TP1的高低棱镜进行高差测量, 求得hTP2-TP1、h′TP2-TP1。
3)如同2)步, 把TP1的全站仪移到点TP3, 同理测出hTP3-TP4、h′TP3-TP4、hTP4-TP3、h′TP4-TP3……
4)在点TPn对点B进行高差测量, 求得hTPn-B、h′TPn-B。
该方法不需量仪器高, 避免量仪器高对高差测量的影响, 只需在首尾A、B两点用强制对中杆对中,但需使A、B两点仪器高高度相同[2-4]。则有:
| $ {h_{A-T{P_1}}} = {D_{A-T{P_1}}}\tan { \propto _{A-T{P_1}}} + {i_A} - {v_{T{P_1}}} $ | (1) |
式中,hA-TP1为观测点A到目标点TP1的高差;DA-TP1为观测点A点到目标点TP1的平距;∝A-TP1为测点A到目标点TP1的竖直角;iA为观测点A的仪器高;vTP1为目标点TP1的棱镜高。
| $ h{'_{A-T{P_1}}} = D{'_{A-T{P_1}}}\tan \propto {'_{A-T{P_1}}} + i{'_A} - v{'_{T{P_1}}} $ | (2) |
| $ {h_{T{P_1}-T{P_2}}} = {D_{T{P_1}-T{P_2}}}\tan { \propto _{T{P_1}-T{P_2}}} + {i_{T{P_1}}} - {v_{T{P_2}}} $ | (3) |
| $ {h_{T{P_2}-T{P_1}}} = {D_{T{P_2}-T{P_1}}}\tan { \propto _{T{P_2}-T{P_1}}} + {i_{T{P_2}}} - {v_{T{P_1}}} $ | (4) |
| $ h{'_{T{P_1}-T{P_2}}} = D{'_{T{P_1}-T{P_2}}}\tan \propto {'_{T{P_1}-T{P_2}}} + i{'_{T{P_1}}} - v{'_{T{P_2}}} $ | (5) |
| $ h{'_{T{P_2}-T{P_1}}} = D{'_{T{P_2}-T{P_1}}}\tan \propto {'_{T{P_2}-T{P_1}}} + i{'_{T{P_2}}} - v{'_{T{P_1}}} $ | (6) |
由式(3)和式(4)得:
| $ \begin{array}{*{20}{l}} {\overline {{h_{T{P_1}-T{P_2}}}} = \frac{{{h_{T{P_1}-T{P_2}}}-{h_{T{P_2} - T{P_1}}}}}{2}}\\ {\frac{1}{2}\left( {{D_{T{P_1} - T{P_2}}}\tan { \propto _{T{P_1} - T{P_2}}} + {i_{T{P_1}}} - {v_{T{P_2}}} - } \right.}\\ {\left. {{D_{T{P_2} - T{P_1}}}\tan { \propto _{T{P_2} - T{P_1}}} + {i_{T{P_2}}} - {v_{T{P_1}}}} \right)} \end{array} $ | (7) |
同理可求出
| $ \overline {{h_{T{P_n}-B}}} = {D_{T{P_n}-B}}\tan { \propto _{T{P_n}-B}} + {i_{T{P_n}}} - {v_B} $ | (8) |
| $ \overline {{h_{T{P_n}-B}}} ' = D{'_{T{P_n}-B}}\tan \propto {'_{T{P_n}-B}} + i{'_{T{P_n}}} - v{'_B} $ | (9) |
因为首尾A、B两点用强制对中杆使其目标高相同,所以vA=vB, v′A=v′B。将上述各式相加可以消除v、v′、i和i′,求出hAB、h′AB:
| $ \begin{array}{*{20}{l}} {{h_{AB}} = \frac{1}{2}\left( {{h_{A-T{P_1}}} + \overline {{h_{T{P_1}-T{P_2}}}} } \right. + \overline {{h_{T{P_2}-T{P_3}}}} + }\\ {\left. {\;\;\;\;\; \cdots + {h_{T{P_n} - B}}} \right)} \end{array} $ | (10) |
| $ \begin{array}{*{20}{l}} {h{'_{AB}} = \frac{1}{2}\left( {h{'_{A-T{P_1}}} + \overline {{h_{T{P_1}-T{P_2}}}} } \right.' + \overline {{h_{T{P_2}-T{P_3}}}} ' + }\\ {\left. {\;\;\;\;\; \cdots + \overline {{h_{T{P_n} - B}}} '} \right)} \end{array} $ | (11) |
| $ \overline {{h_{AB}}} = \frac{{{h_{AB}} + h{'_{AB}}}}{2} $ | (12) |
由以上hAB、h′AB公式可知, 所求的高差与仪器高和目标高无关, 可以消除仪器高和目标高对测量高差的影响。测量的成果精度只与距离和竖直角有关。采用全站仪同时对向观测, 观测条件基本是一致的, 因此可以大大削弱距离对测量精度的影响, 同时也可以大大削弱或基本消除大气垂直折光的影响, 所以这里就不考虑大气折光对高程测量的影响。为了提高测量精度, 同测段间还可以进行多测回观测[5, 6]。
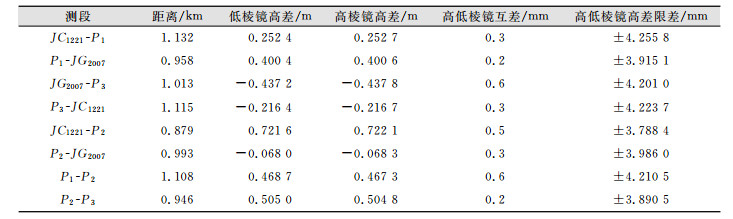
2 实例分析对天津某高速公路项目,从相关部门获取附近两个已知控制点JC1221和JG2007, 二者高程分别为10.388 m和9.735 m。测量仪器采用莱卡0.5″级测量机器人,水准控制网采用网型布设,且点位分布均匀,对二者采用免仪器高、目标高同时对向三角高程观测。网型示意图如图 2所示。经计算,8个测段的数据观测情况如表 1所示。
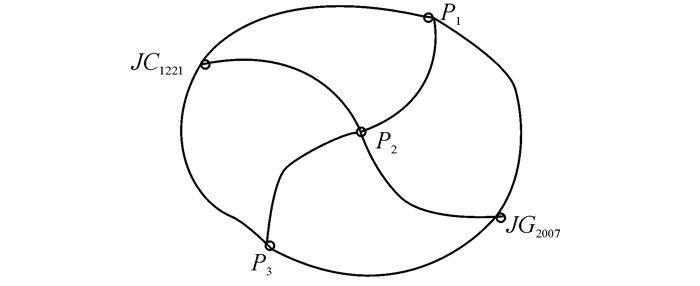 |
| 图 2 水准路线示意图 Figure 2 Level of the Circuit Diagram |
| 表 1 测段观测数据表 Table 1 Observation Data |
 |
每km水准测量偶然中误差计算公式为:
| $ {M_\Delta } = \pm \sqrt {\left[{\frac{{\Delta \Delta }}{R}} \right]/\left( {4N} \right)} $ | (13) |
式中,Δ为测段往返测高差不符值;R为测段长度;N为测段数。
每km水准测量全中误差计算公式为:
| $ {M_W} = \pm \sqrt {\left[{\frac{{WW}}{F}} \right]/N} $ | (14) |
式中,W为水准闭合环差;F为水准环线周长;N为水准环数。
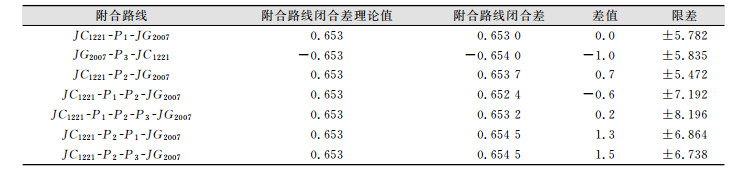
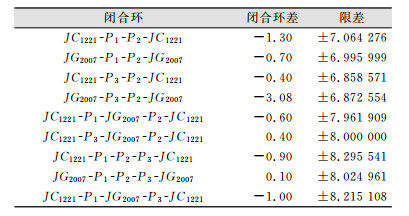
从表 2、表 3可以看出,水准网中各附合水准路线与闭合水准路线闭合差均满足限差要求。
| 表 2 附合路线数据检核表/mm Table 2 Data Check List of Contact Leveling Line/mm |
 |
| 表 3 闭合路线数据检核表/mm Table 3 Data Check List of Closed Leveling Line/mm |
 |
经计算,本次测量任务每km水准测量偶然中误差和每km水准测量全中误差如表 4所示。
| 表 4 水准测量每km偶然中误差与全中误差对照表/mm Table 4 Accident Mean Square Error and Complete Mean Square Error Per Kilometer of Leveling/mm |
 |
从表 4可知,每km水准测量偶然中误差、每km水准测量全中误差以及附合路线闭合差均满足限差要求,本次实验数据精度能够达到二等水准测量的精度要求,使得测量精度得到显著提高。
3 结束语高低双棱镜三角高程测量方法除首末站外无需测量仪器高,并且通过高低棱镜对向观测有效地消除了传统三角高程测量中存在的球气差、仪器高和觇标高量测误差,提高了测量速度和观测精度。
| [1] |
潘正风, 程效军, 杨正尧, 等.
数字测图原理与方法[M]. 武汉: 武汉大学出版社, 2004 .
Pan Zhengfeng, Cheng Xiaojun, Yang Zhengyao, et al. Principles and Methods of Digital Mapping[M]. WuHan: Wuhan University Press, 2004 . |
| [2] |
翟翊, 侯钦涛. 三角高程测量计算公式讨论[J].
测绘通报,2004,(3) : 11–13.
Zhai Yi, Hou Qintao. On the Formula of Trigonometric Leveling[J]. Bulletin of Surveying and Mapping,2004,(3) : 11–13. |
| [3] |
徐汉涛. 改变觇标高度的三角高程测量[J].
南通大学学报(自然科学版),2004,3(4) : 45–47.
Xu Hantao. A Trigonometric Leveling Method by Changing the Height of Measuring Mark[J]. Journal of Nantong Institute of Technology (Natural Science),2004,3(4) : 45–47. |
| [4] |
黄满太.全站仪中间法在精密三角高程测量中的应用[D].长沙:中南大学, 2008 Huang Mantai. Applied Research of the Total Station Elevation Surveying Using Midway Method in Precise Trigonometric Leveling[D]. Changsha: Central South University, 2008 http://d.wanfangdata.com.cn/Thesis_Y1327673.aspx |
| [5] |
魏垂场. 用免仪器高、目标高同时对向三角高程观测法替代二等、三等水准测量的研究[J].
水利与建筑工程学报,2008,6(3) : 85–87.
Wei Chuichang. Study on Replacing Second and Third Order Leveling by Subtending Simultaneity Observation of Trigonometric Leveling Without Height of Total Station Instrument and Its Goal[J]. Journal of Water Resources and Architectural Engineering,2008,6(3) : 85–87. |
| [6] | Zhang Zhenglu, Zhang Kun, Deng Yong, et al. Research on Precise Trigonometric Leveling in Place of First Order Leveling[J]. Geo-Spatial Information Science,2005,(4) : 235–239. |
 2016, Vol. 41
2016, Vol. 41

