2. 中国科学院 自动化研究所, 北京 100190
为检测图像的旋转对称中心和旋转对称角,通过引入旋转对称能量的概念,提出了一种新的旋转对称性检测算法.该算法分为3个步骤:1)对图像中任一位置,计算该位置处的旋转对称能量和旋转对称角;2)计算各点处的旋转对称能量获取整幅图像对应的旋转对称能量图;3)在旋转对称能量图上进行局部极大值检测获得旋转对称图形的旋转对称中心并确定旋转对称角度.实验结果表明,该算法不仅能够准确鲁棒地检测出旋转对称图形的旋转对称中心与旋转对称角,还能成功应用于图像修复.
2. Institute of Automation, Chinese Academy of Sciences, Beijing 100190, China
Rotation symmetry is significant for image understanding, object recognition and image restoration. In order to detect the center and angle of rotation symmetry in the image, a new rotation symmetry detection algorithm is presented by introducing the rotation symmetry energy. The proposed method consists of three steps:1) Compute the rotation symmetry energy and rotation symmetry angle for each position in the image; 2) Calculate the rotation symmetry energy map of the whole image; 3) Detect the local maxima in the rotation symmetry energy map to locate the rotation symmetry center, and acquire the rotation symmetry angle simultaneously. Experiments illustrate that the proposed algorithm can be not only used to detect the rotation symmetry center and angle of the rotation symmetry graphic, but also applied to image restoration successfully.
一些学者针对图像旋转对称性进行了深入研究. Cornelius等[1]采用局部不变特征进行旋转对称检测. Yip[2]利用霍夫变换在平行投影条件下进行旋转对称检测. Carlsson[3]提出了一种基于透视空间的旋转对称描述. Lee等[4]将旋转对称检测问题转化为一维平移对称性问题加以解决. Yip[5]提出了一种遗传傅里叶描述子从部分遮挡或开轮廓中检测旋转对称性. Liu等[6]基于二面角和边缘特征进行剪纸图案检测. Venkatesh等[7]提出了一种在严格闭合的情况下实现旋转对称性检测的算法. Masuda等[8]提出一种从灰度图像中检测旋转对称和镜射对称的方法.与已有方法完全不同,笔者通过定义旋转对称能量来进行旋转对称检测:第1节引入旋转对称能量;第2节介绍检测算法;第3节将算法应用于图像修复;最后是结束语.
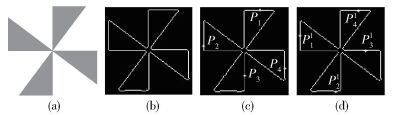
1 旋转对称能量1.1 基本思想对图像中的一个旋转对称目标,如果将该目标绕其旋转中心旋转特定角度(旋转对称角),则旋转后得到的图形与原图形完全一致.可利用边缘点对这种旋转一致性进行度量:将目标上各边缘点绕特定位置旋转特定角度,旋转后各点对应位置处边缘点越多,则说明所述特定位置是旋转中心的可能性越大,同时该旋转角度即是对应的旋转对称角.如图 1(a)所示为旋转角为90°的旋转对称图形. 图 1(b)所示为对应的边缘检测图;图 1(c)中指定了4个边缘点P1,P2,P3和P4,图 1(d)中的P11,P21,P31和P41是P1,P2,P3和P4围绕中心逆时针旋转90°的位置.显然旋转后4个点对应新位置依旧是边缘点.下面通过两组讨论引入旋转对称能量.
|
图 1 大小为51×51的模拟图 |
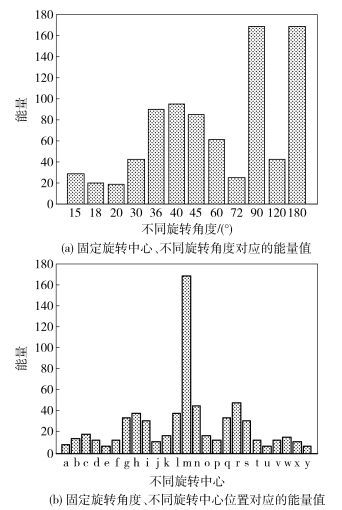
1) 固定旋转中心,设定旋转中心位置为图像中心(26, 26),调整旋转角度依次为15°、18°、20°、30°、36°、40°、45°、60°、72°、90°、120°、180°,分别统计旋转前后重合边缘点个数,结果如图 2(a)所示.
|
图 2 不同情况下的能量值 |
2) 固定旋转角度,设定旋转角度为90°,设定旋转中心分别为a(6, 6)、b(6, 16)、c(6, 26)、d(6, 36)、e(6, 46)、f(16, 6)、g(16, 16)、h(16, 26)、i(16, 36)、j(16, 46)、k(26, 6)、l(26, 16)、m(26, 26)、n(26, 36)、o(26, 46)、p(36, 6)、q(36, 16)、r(36, 26)、s(36, 36)、t(36, 46)、u(46, 6)、v(46, 16)、w(46, 26)、x(46, 36)、y(46, 46),统计旋转后重合的边缘点个数,结果如图 2(b)所示.
可以看出,当旋转角度为90°和180°且旋转中心为(26, 26) 时重合边缘点个数能够达到最大值.给定一个旋转中心和旋转角,将一个局部图像旋转前后重合的边缘点个数定义为旋转对称能量.
1.2 具体构造流程对于图像中指定位置(x0, y0),将以(x0, y0)为中心,R为半径的圆形区域称为其支撑区域.将支撑区域内边缘点(xi, yi), i=1, 2, …, N绕(x0, y0)旋转θm, m=1, 2, …, M后得到新坐标.

|
(1) |
将支撑区域中所有边缘点均绕中心旋转θm,判定旋转前后边缘点的重合性(旋转后新位置是否依旧是边缘点):
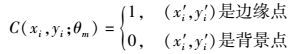
|
(2) |
对于指定旋转角度θm,将支撑区域内所有边缘点旋转前后的重合性进行累加,有
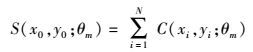
|
(3) |
对于任一位置(x0, y0),计算其在不同旋转角度下的重合性,记重合性的最大值为该点处的旋转对称能量E,对应的旋转角称为旋转对称角θ.

|
(4) |
对称目标中重复的部分称为对称单元,对称单元数为M与旋转对称角θm之间的关系为
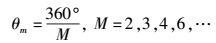
|
(5) |
考虑取整与实际情况,旋转对称角度θm可取15°、18°、20°、30°、36°、40°、45°、60°、72°、90°、120°、180°,对应M分别为24、20、18、12、10、9、8、6、5、4、3、2,实际检测时算法只需考虑这12种情况即可.
2 旋转对称性检测基于旋转对称能量的旋转对称性检测算法主要包括3个步骤.
步骤1 对于图像中任一位置,利用式(4) 计算该点处的旋转对称能量和旋转对称角;
步骤2 计算各位置处的旋转对称能量获取整幅图像对应的旋转对称能量图;
步骤3 在旋转对称能量图上进行局部极大值检测获得旋转对称中心,并获得相应的旋转对称角.
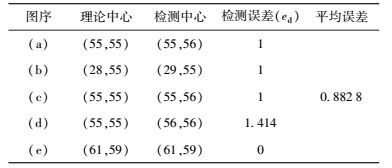
2.1 模拟图像实验模拟图像可直接利用理论中心位置与检测中心位置的误差来度量算法准确性.记理论中心位置为(x0, y0),算法检测中心位置为(x, y),则算法中心检测误差定义为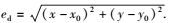
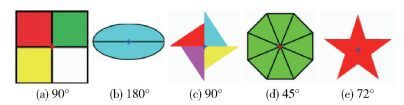
|
图 3 模拟图像检测结果 |
|
|
表 1 理论中心与检测中心的误差 |
为验证算法对噪声与图像模糊的鲁棒性,算法进一步在上述5幅模拟图像进行了噪声和模糊测试,中心检测误差结果如图 4所示.可以看出,图像噪声和模糊对算法性能影响不大,分析其主要原因是旋转对称能量是基于图像边缘进行计算的,常见边缘检测算法经过高斯平滑后均对噪音和模糊具有较好鲁棒性.
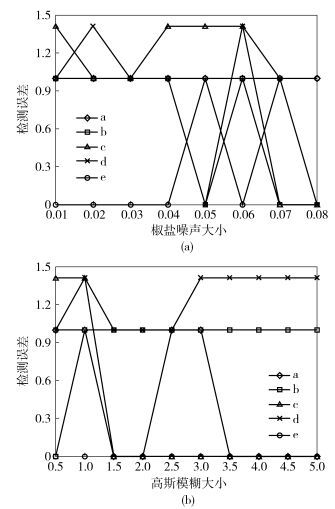
|
图 4 图像噪声和模糊实验结果 |
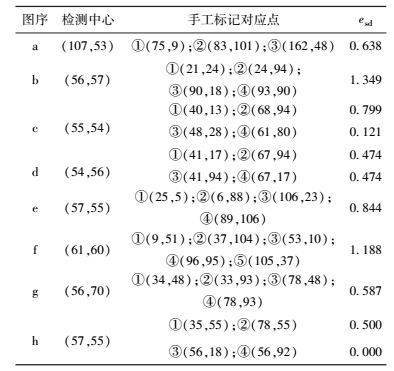
真实图像上采用间接方法进行准确性度量.首先手工在目标图像上选择一组关键点(ri, ci),i=1, 2, …, N,计算各关键点到检测中心的距离di=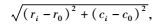

|
图 5 真实图像检测结果 |
|
|
表 2 图 5中检测中心到对应点的距离标准差 |
本节将旋转对称检测算法应用于图像修复并验证算法在图像存在缺损时的鲁棒性.具体步骤如下:首先进行旋转对称性检测,获得旋转对称中心(x0, y0)及旋转对称角为θ.将图像中任一点Pi(xi, yi),绕对称中心(x0, y0)旋转θ得到Pi(xi1, yi1):
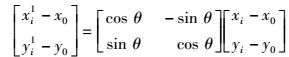
|
(6) |
对比Pi和Pi1的灰度值,如果两点灰度值相同或相似,说明Pi点不是有缺损的点;反之,则说明Pi和Pi1中有一点为缺损点并进行进一步验证.将Pi1绕旋转对称中心旋转θ角得到Pi2(xi2, yi2):
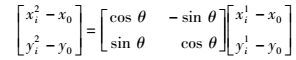
|
(7) |
对比Pi、Pi1和Pi2的灰度值,如果Pi1和Pi2的灰度值相同或相似,则Pi点是缺损点并将Pi1或Pi2的灰度值赋给Pi;如果Pi和Pi2的灰度值相同或相似,则Pi1点是缺损点并将Pi或Pi2的灰度值赋给Pi1.重复上述过程可实现图像缺损修复.
图 6给出4组图像修复实验结果.可以看出,缺损时算法不仅能成功检测出旋转对称中心和旋转对称角,而且能够成功用于缺损修复.

|
图 6 图像修复实验 |
通过引入旋转对称能量的概念,提出了一种新型的旋转对称性检测算法,该算法不仅可准确检测出图像中旋转对称目标的旋转对称中心和旋转角,还可成功应用于图像缺损修复.下一步将重点研究仿射变化下旋转对称图形的检测方法.
| [1] | Cornelius H, Loy G. Detecting rotational symmetry under affine projection[C]//18th International Conference on Pattern Recognition. Hong Kong:IEEE, 2006:292-295. http://yadda.icm.edu.pl/yadda/element/bwmeta1.element.ieee-volume-000000011159-2 |
| [2] | Yip R K K. A Hough transform technique for the detection of parallel projected rotational symmetry[J].Pattern Recognition Letters, 1999, 20(10): 991–1004. doi: 10.1016/S0167-8655(99)00066-5 |
| [3] | Carlsson S. Symmetry in perspective[C]//5th European Conference on Computer Vision. Berlin:Springer, 1998:249-263. |
| [4] | Lee S, Liu Y. Skewed rotation symmetry group detection[J].IEEE Trans. on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1659–1672. doi: 10.1109/TPAMI.2009.173 |
| [5] | Yip R K K. Genetic Fourier descriptor for the detection of rotational symmetry[J].Image and Vision Computing, 2007, 25(2): 148–154. doi: 10.1016/j.imavis.2006.01.024 |
| [6] | Liu Y, Hays J, Xu Y Q, et al. Digital papercutting[C]//International Conference on Computer Graphics and Interactive Techniques. New York:ACM, 2005:99. |
| [7] | Venkatesh M V, Cheung S S. Symmetric shape completion under severe occlusions[C]//2006 IEEE International Conference on Image Processing. Atlanta:IEEE, 2006:709-712. |
| [8] | Masuda T, Yamamoto K, Yamada H. Detection of partial symmetry using correlation with rotated-reflected images[J].Pattern Recognition, 1993, 26(8): 1245–1253. doi: 10.1016/0031-3203(93)90209-F |