研究了由1个单天线的源节点、目的节点、窃听节点和1个多天线的中继节点组成的系统中,通过能量协作增强保密传输性能的问题. 为提高保密速率,中继节点发送经过波束赋形的干扰信号来干扰窃听者. 在中继能量供应受限的情况下,提出一种协作干扰与能量协作相结合的方案. 源端在能量约束范围内采用能量转移的方式为中继提供用于发送干扰信号的能量. 对能量转移量、能量转移时间和干扰信号波束赋形的优化问题进行了求解. 仿真结果表明,在不消耗中继自身能量的条件下,与直接传输相比,能量协作和协作干扰方案能够显著提高系统的保密性能.
It attempts to solve the problem of enhancing physical-layer transmission security based on energy cooperation in the system which consists of one single-antenna source, destination, eavesdropper and one multi-antenna relay. To improve the secrecy rate, the multi-antenna relay transmits beamformed jamming signals to disturb the eavesdropper. A scheme of cooperative jamming with energy cooperation is proposed for the scenario when the energy supply of the relay is limited. Within the scope of the energy constraint, the source provides energy for the relay to transmit jamming signals. The optimal solution is derived for the amount of energy needed to transfer, transferring time and the beamforming vector of the jamming signals. The simulation results show that in the case when no energy of the relay is consumed, the scheme of energy cooperation and jamming can significantly improve the secrecy rate compared with direct transmission.
协作传输是一种有效增强物理层安全的方式,主要技术包括放大转发、译码转发和协作干扰[1]. 在发送信息时加入干扰信号,并合理分配信息信号和干扰信号之间的功率,可以有效提高系统的保密速率[2]. 在传统的协作中,中继帮助用户进行数据协作传输,Gurakan等[3, 4]提出一种无线能量传输的协作方式,节点可以从信号或干扰中提取能量[5]. Yin等[6]考虑发送端以某一速率从外界得到能量,并将其用于通信. Liu等[7]介绍了在无线同时传输信息和能量系统中的物理层安全问题.
笔者考虑能量协作对系统保密速率的影响. 系统中包含单天线源端、合法目的端、非法窃听端,以及多天线中继. 为增强物理层安全传输的性能,系统中的中继采用协作干扰方式,即中继作为辅助干扰者在源端发送信息信号的同时发送干扰信号,以混淆窃听者. 考虑中继的能量供应受到限制,仅能在不消耗自身能量的前提下帮助源端干扰窃听者,因此源端需向中继提供能量. 笔者在可以获得所有信道状态信息的前提下、在源端满足一定的能量约束条件下,对能量转移、功率分配、干扰信号的产生和发送方案进行优化,使系统获得最大保密速率. 笔者先给出系统模型和协作方案,然后给出在能量转移时间一定和变化时能量协作中的能量转移量、干扰噪声的波束赋形矢量的优化过程,并获得最优保密速率,最后给出仿真结果.
1 系统模型和协作方案 1.1 系统模型笔者考虑1个4节点模型,即包含1个源节点S、1个目的节点D、1个窃听节点E和1个中继节点R. 源端、窃听端和目的端分别装备1根全向天线,而中继装有N>1根天线. 所有的信道都是平坦衰落、准静态、无记忆的. 定义hsd为源端到目的端的信道系数,hse为源端到窃听端的信道系数. 中继到目的端和中继到窃听端的信道系数分别定义为hrd和hre,且hrd∈CN×1,hre∈CN×1. 假设中继已知所有信道状态信息,各节点的噪声都是零均值的复高斯白噪声且噪声方差为σ2.
1.2 协作方案系统中的中继采用协作干扰模式. 由于中继的能量供应受限,其发送干扰信号的前提是不消耗自身能量. 因此,源端需转移一部分能量给中继供其发送干扰信号. 设传输中每个时隙的长度为T,源端在1个时隙内能使用的能量限制为Es.
将1个时隙分为2部分. 源端在时隙的前TE内将δ能量发送给中继,能量传输效率为α(0≤α≤1). 在剩下的T-TE时间内源端向目的端发送保密信息,同时中继发送波束赋形后的干扰信号. 为最大化系统的保密速率,需要对中继发送干扰信号的波束赋形矢量进行设计,并优化源端向中继的能量转移量.
设源端发送的符号为x,中继发送的干扰信号为z. z为零均值、单位方差的圆对称复高斯随机变量. 目的端接收的信号为
| ${y_d} = \sqrt {\frac{{{E_s} - \delta }}{{T - {T_E}}}} {h_{sd}}x + h_{rd}^Hwz + {n_d}$ | (1) |
其中:nd为目的端的噪声,w为干扰信号的波束赋形矢量. 中继的发送功率限制为$Tr\left( {w{w^H}} \right)\frac{{\alpha \delta }}{{T - {T_E}}}$. 类似地,窃听端接收到的信号为
| ${y_e} = \sqrt {\frac{{{E_s} - \delta }}{{T - {T_E}}}} {h_{se}}x + h_{re}^Hwz + {n_e}$ | (2) |
其中ne为窃听端的噪声.
2 保密速率的优化分析分析可知,影响保密速率的因素有干扰信号的波束赋形矢量w、能量转移量δ和能量转移时间TE.
2.1 能量转移时间固定对于能量协作的方案,源端和中继处存在不同于一般协作的限制条件. 首先,考虑能量转移时间固定的问题. 为了简化问题求解,令wHhrd=0,即满足目的端不受干扰. 优化问题可用公式表示为
| $\begin{array}{l} \begin{array}{*{20}{c}} {\max }\\ {w,\delta } \end{array}{R_s} = \frac{{T - {T_E}}}{T}\log \left( {1 + \frac{{\frac{{{E_s} - \delta }}{{T - {T_E}}}{{\left| {{h_{sd}}} \right|}^2}}}{{{\sigma ^2}}}} \right) - \\ \frac{{T - {T_E}}}{T}\log \left( {1 + \frac{{\frac{{{E_s} - \delta }}{{T - {T_E}}}{{\left| {{h_{se}}} \right|}^2}}}{{\left| {{w^H}{h_{re}}} \right| + {\sigma ^2}}}} \right)\\ s.t.\;\;Tr\left( {w{w^H}} \right) = \frac{{\alpha \delta }}{{T - {T_E}}}\\ {w^H}{h_{rd}} = 0\\ 0 \le \delta < {E_s} \end{array}$ | (3) |
在最优化保密速率时,需要求解w和δ两个优化变量,由于这2个变量不存在相互约束的关系,故可分2步解决该优化问题.
分析式(3)可知,保密速率Rs为关于|wHhre|2的增函数. 因此,求解该优化问题时,可先把变量δ看作常数,将w的最优值以δ的函数形式表示出来. 这样式(3)中的问题可等效为
| $\begin{array}{l} \begin{array}{*{20}{c}} {\max }\\ w \end{array}{\left| {{w^H}{h_{re}}} \right|^2}\\ s.t.{w^H}{h_{rd}} = 0\\ \;\;\;\;\;\;\;\;\;Tr\left( {w{w^H}} \right) = \frac{{\alpha \delta }}{{T - {T_E}}} \end{array}$ | (4) |
hrd零空间的投影矩阵为V=IN-hrd(hrdHhrd)-1×hrdH. 对于任意满足限制条件wHhrd=0的w,都有Vw=w. 于是,式(4)中最大化|wHhre|2等价为最大化|wHVhre|2. 根据向量数量积的定义易知,当2个向量共线时,数量积有最大值. 因此,最优波束赋形矢量为
| $w = \frac{{\sqrt {{P_r}} }}{{\left\| {V{h_{re}}} \right\|}}V{h_{re}} = \mu {\left\| {{h_{rd}}} \right\|^2}{h_{re}} - \mu _{rd}^H{h_{re}}{h_{rd}}$ | (5) |
其中Pr为干扰信号的功率. 系数为
| $\mu = \sqrt {\frac{{\frac{{\alpha \delta }}{{T - {T_E}}}}}{{{{\left\| {{h_{rd}}} \right\|}^4}{{\left\| {{h_{re}}} \right\|}^2} - {{\left\| {{h_{rd}}} \right\|}^2}{{\left| {h_{rd}^H{h_{re}}} \right|}^2}}}} $ | (6) |
将w的表达式代入式(3),整理得到
| ${R_s}\left( \delta \right) = \frac{{T - {T_E}}}{T}\log \left( {\frac{{{e_0} + {e_1}\delta + {e_2}{\delta ^2}}}{{{f_0} + {f_1}\delta }}} \right)$ | (7) |
下面讨论式(7)在δ的值域[0,Es]内的最大值问题. 令$F\left( \delta \right) = \frac{{{e_0} + {e_1}\delta + {e_2}{\delta ^2}}}{{{f_0} + {f_1}\delta }}$,则
| $\frac{{\partial F}}{{\partial \delta }} \propto A{\delta ^2} + B\delta + C$ | (8) |
其中:A=e2f1,B=2e2f0,C=e1f0-e0f1.
当B2-4AC≥0时,式(7)存在2个不等或相等的极值点x1和x2. 使保密速率最大的δ值将在0、Es、x1、x2四个点上取得. 当B2-4AC>0时,式(7)不存在极值点,它表示的函数是单调的. 在这种情况下,若A<0,则最优的能量转移量为0,即中继不发送干扰;若A>0,则最优的能量转移量为Es. 需注意,实际情况中δ不可能取Es,因为此时源端将全部能量转移给中继,没有用于发送信息的能量.
最优的能量转移量δ一定在0、x1、x2这3个点中选取,且应为实数. 综合以上条件,可以得到最优的能量转移量$\hat \delta $.
2.2 能量转移时间可变实际上,能量转移所需时间、能量转移量与能量转移速率有关. 能量转移时间固定,可能导致所需能量转移不完或时间浪费. 因此,更优的方案应该能灵活地分配能量转移的时间长度.
设能量转移速率为v,则能量转移需要的时间为${T_E} = \frac{\delta }{v}$. 在能量转移时间可变的情况下,保密速率达到最大的优化问题为
| $\begin{array}{l} \begin{array}{*{20}{c}} {\max }\\ {w,\delta } \end{array}{R_s} = \frac{{T - \frac{\delta }{v}}}{T}\log \left( {1 + \frac{{\frac{{{E_s} - \delta }}{{T - \frac{\delta }{v}}}{{\left| {{h_{sd}}} \right|}^2}}}{{{{\left| {{w^H}{h_{rd}}} \right|}^2} + {\sigma ^2}}}} \right) - \\ \frac{{T - \frac{\delta }{v}}}{T}\log \left( {1 + \frac{{\frac{{{E_s} - \delta }}{{T - \frac{\delta }{v}}}{{\left| {{h_{se}}} \right|}^2}}}{{{{\left| {{w^H}{h_{re}}} \right|}^2} + {\sigma ^2}}}} \right)\\ s.t.\;\;\;Tr\left( {w{w^H}} \right) = \frac{{\alpha \delta }}{{T - \frac{\delta }{v}}}\\ 0 \le \delta < {E_s},T - \frac{\delta }{v} \ge 0 \end{array}$ | (9) |
与2.1节方法相同,很容易得到在能量转移时间可变情况下的波束赋形矢量w. 将w关于δ的函数带入式(9)中,整理得到Rs关于δ的函数为
| ${R_s}\left( \delta \right) = \left( {1 - \frac{\delta }{{vT}}} \right)\log \left( {\frac{{{{\tilde e}_0} + {{\tilde e}_1}\delta + {{\tilde e}_2}{\delta ^2}}}{{{{\tilde f}_0} + {{\tilde f}_1}\delta + {{\tilde f}_2}{\delta ^2}}}} \right)$ | (10) |
在源端的能量约束内,若能量转移量过大、能量转移时间过长、源端发送信息信号的能量和时间都相对很小,保密速率必然较小;反之,若能量转移量过小、中继发送干扰信号的能量过小、从而对窃听端的干扰很小,此时的保密速率也不会较大. 因此,在能量约束范围内必定存在一个最优的能量转移量,使系统的保密速率达到最大值.
由于式(10)中的δ最优值的闭式解很难给出,所以这里采用1维搜索的方法,在δ的值域内向着使式(10)的值变大的δ的方向逐渐缩小搜索范围,最终得到最优的δ值. 随之也就可以确定能量转移时间的分配. 将最优能量转移量带入式(5)和式(10),即得到最优波束赋形矢量和最大保密速率.
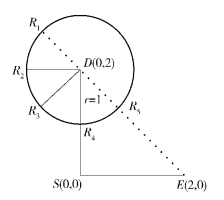
3 仿真结果及分析节点位置如图 1所示. 中继与目的端距离1 m. 不同节点的任意2个收发天线间的信道衰落为h=βd-c/2,其中d m为2个节点间的距离,c=3.5为路径损耗指数,β为小尺度衰落因子. 令σ2=1,T=1,Es=100,α=0.8. 中继的天线数分别为3、4、5.
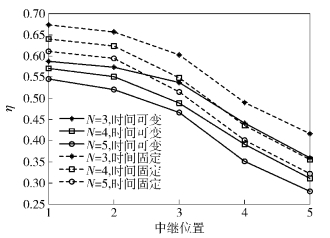
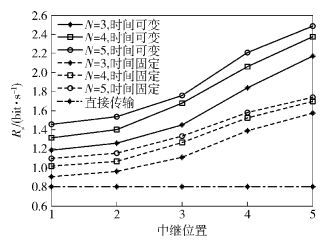
图 2和图 3分别仿真了在TE=0.5和v=200时最优的η=δ/Es和保密速率. 中继从R1移动到R5. 结果显示,随着中继到窃听端距离的减少,能量协作中需由源端向中继转移的能量的比例逐渐减少,而保密速率将逐渐变大. 能量转移时间可变的系统由于优化了能量转移和信息传输的时间安排,避免了时间浪费,同时合理安排了能量转移量,其性能要优于能量转移时间固定的系统.
分析图 2和图 3可知,中继节点天线数N越大,波束赋形的效果越好,干扰信号以较小的功率就可以得到好的干扰效果,所以需要转移的能量减少,源端发送信号的能量增加,因此系统获得的保密速率也增大.
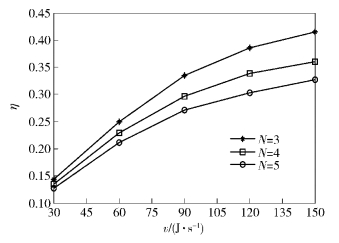
图 4和图 5显示了能量转移比例和系统保密速率的关系. 中继固定在R4位置上,其他条件保持不变. 能量转移速率的增加,可使系统更快地完成能量协作的过程. 因而,可在更宽的范围内进行能量转移量优化. 同时,也可拥有更多的时间用于信息的传输. 随着能量转移速率的增加,能量转移在时间上受到的限制减少,这样可以更合理地分配转移的能量,获得更高的保密速率.
4 结束语
笔者研究了采用能量协作和协作干扰技术的物理层安全问题,针对最大化保密速率问题对能量转移量、能量转移时间和干扰信号的波束赋形矢量进行优化. 讨论了在能量传输时间固定和可变2种情况下的优化问题. 通过仿真验证了笔者提出的协作方案对保密速率的改善显著.
| [1] | Dong Lun, Han Zhu, Petropulu A P, et al. Improving wireless physical layer security via cooperating relays[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1875-1888.[引用本文:1] |
| [2] | 都晨辉, 宋梅, 王莉, 等. 基于Stackelberg博弈的协作干扰策略[J]. 北京邮电大学学报, 2014, 37(5): 11-15. Du Chenhui, Song Mei, Wang Li, et al. Improved physical layer security with cooperative jamming based on Stackelberg game[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(5): 11-15.[引用本文:1] |
| [3] | Gurakan B, Ozel O, Yang Jing, et al. Energy cooperation in energy harvesting wireless communications[C]//2012 IEEE International Symposium on Information Theory Proceedings (ISIT). [S.l.]: IEEE, 2012: 965-969. [引用本文:1] |
| [4] | Gurakan B, Ozel O, Yang Jing, et al. Energy cooperation in energy harvesting communications[J]. IEEE Transactions on Communications, 2013, 61(12): 4884-4898.[引用本文:1] |
| [5] | Gu Yanju, Aissa S. Interference aided energy harvesting in decode-and-forward relaying systems[C]//2014 IEEE International Conference on Communications (ICC). [S.l.]: IEEE, 2014: 5378-5382.[引用本文:1] |
| [6] | Yin Sixing, Zhang Erqing, Li Ji, et al. Throughput optimization for self-powered wireless communications with variable energy harvesting rate[C]//2013 IEEE Wireless Communications and Networking Conference (WCNC). [S.l.]: IEEE, 2013: 830-835.[引用本文:1] |
| [7] | Liu Liang, Zhang Rui, Chua Keechaing. Secrecy wireless information and power transfer with MISO beamforming[J]. IEEE Transactions on Signal Processing, 2014, 62(7): 1850-1863.[引用本文:1] |