2. 中国电子科技集团公司 第39研究所, 西安 710065
对突发毁伤条件下的网络性能进行实时监测,获取其动态变化曲线;在此基础上,首先依据网络业务的服务质量(QoS)要求,科学设定性能参量的上、下QoS边界值;其次构建网络可生存性的评价指标体系,分析了评价指标与网络性能参量之间的映射关系,并给出指标量化算法;最后结合突发事件的威胁度,对网络总体可生存性进行综合评价,实例分析表明,评价指标的计算过程较好避免了人为主观因素的影响,其评估结果更为客观、有效.
2. China Electronics Technology Group, No.39 Research Institute, Xi'an 710065, China
Network performance parameters were monitored in real time under conditions of the burst damage, and its dynamic curve was got. On the basis, firstly, the upper and lower boundaries of performance parameters were set scientifically according to the quality of service requirements of network services; then, the evaluation index system of network survivability was built. The mapping relationship between evaluation index and network performance parameters was analyzed, and the quantitative calculation method of index was given; finally, the overall survivability was evaluated comprehensively according to the threat level of emergencies. Analysis shows that the proposed method is scientific and effective.
目前网络可生存性评估方法有两类:一是基于系统状态变迁的建模方法[1, 2, 3, 4, 5],数学理论较为成熟,但此仍存在模型参数确定难、模型状态空间爆炸等问题;二是基于指标体系构建的综合评估方法[6, 7],此类方法构建多层次的评价指标体系,所得评估结果较为科学合理,但仍存在指标体系不统一、不完善,以及指标量化易受人为主观因素影响等问题.
针对以上问题,提出一种性能监测下的IP网络可生存性评估方法. 采用Netperf获取网络性能参量在突发毁伤条件下的变化曲线;构建可生存性评价指标体系,对评价指标与网络性能之间的映射关系进行分析,并给出指标量化算法;最后通过综合加权计算得到网络总体可生存性大小.
1 网络生存状态描述 1.1 网络性能参量釆用Netperf实时监测如下网络性能.
1) 传输时延
传输时延是指一个分组从源节点发送到目的节点接收之间的时间差. 实时视频会议、网络电话等应用都较为关注分组的时延大小.
2) 时延抖动
时延抖动是指前后两个分组之间的不同时延差. 在实时信息交互情景下,时延抖动更受关注,若时延抖动过大,则需在播放前做较大的缓冲,否则会造成画面不连续,严重影响播放质量.
3) 丢包率
丢包率是指特定时间内丢失的分组占传输数据总量的比例. 在网络传输电视信号时,若发生丢包,就会出现马赛克现象,甚至无法正常播放.
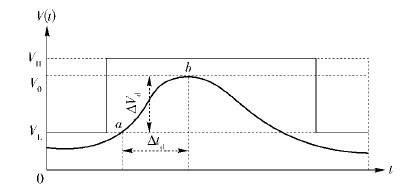
1.2 性能监测下的网络生存状态描述网络突发毁伤时,网络性能变化如 图 1所示.
图 1中横轴为时间t,纵轴为某性能测量值V(t),为V(t)设定VH和VL两个定值,将其作为网络生存状态转换的边界值. 获取性能变化曲线有如下几步:
步骤1 采用时间均值采样得到性能变化折线;
步骤2 选取数个特殊点,如性能V(t)首次降至VL的点A(ta,VL),V(t)首次降至VH的点B(tb,VH),V(t)跌落最低点C(tc,V0),V(t)最终一次回升至VH的点D(td,VH),V(t)最终一次回升至VL的点E(te,VL);
步骤3 釆用平滑曲线依次连接以上各点,从而获取网络性能的变化曲线.
基于该曲线对网络生存状态进行描述,即当V(t)≤VL时,下降段描述为“正常状态”,回升段描述为“自适应状态”,当VL<V(t)≤VH时, 下降段描述为“抵抗状态”,回升段描述为“恢复状态”,当V(t)>VH时,则认为网络处于“毁伤状态”.
2 网络可生存性评估方法 2.1 构建网络可生存性评价指标借鉴Ellison[8]提出的可生存系统必须具备的4个基本属性作为评价指标. 可识别性(S):主要用于反映网络系统对突发毁伤事件的检测灵敏度;可抵抗性(D):主要用于反映网络系统在突发毁伤条件下尽量保持网络性能稳定并继续提供基本服务的能力;可恢复性(H):指网络系统在毁伤状态下的自我修复能力;自适应性(A):指网络系统对新发现毁伤事件特征进行自学习,并对其形成一定免疫的能力.
2.2 可识别性指标量化方法对于突发毁伤事件,网络越早发现越好,因此可识别性指标可采用识别时间长短来度量. 设定识别灵敏度区间[Φ,φ],当识别时间小于Φ时,认为识别灵敏度高,有利于毁伤事件的及时处置;当识别时间大于φ时,认为识别灵敏度低,即毁伤事件所造成的破坏已难以逆转. 若识别时间记为t,则可识别性指标S可按下式正则化为[0,1]间的量化值.
| $ S = \left\{ \begin{array}{l} 1\;\;\;\;t \le \phi \\ - \frac{1}{{\varphi - \phi }} + \frac{\varphi }{{\varphi - \phi }}\;\;\;\;\;\phi < t \le \varphi \\ 0,\;\;\;t > \varphi \end{array} \right. $ | (1) |
抵抗状态下的性能变化如 图 2所示. 图中曲线a—b段代表网络处于“抵抗状态”,性能V(t)的下降速率从一定程度上反映出网络的抵抗能力,即曲线a—b变化越陡,则表示网络的抵抗能力越差,曲线a—b变化越缓,则表示网络的抵抗能力越强,因此可抵抗性指标D可量化为
| $ D = \left\{ \begin{array}{l} 1,\;\;\;{V_0} \le {V_L}\\ {e^{ - \left( {\Delta {V_d}/\Delta {t_d}} \right)}},\;\;\;{V_L} < {V_0} \le {V_H}\\ 0,\;\;\;\;{V_0} \le {V_H}\; \end{array} \right. $ | (2) |
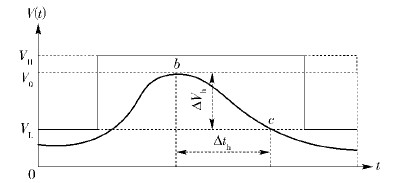
恢复状态下的性能变化如 图 3所示. 图 3中曲线b—c段代表网络处于“恢复状态”,性能V(t)的回升速率从一定程度上反映出网络的恢复能力,即曲线b—c变化越陡,则表示网络的恢复自愈能力越好,曲线b—c变化越缓,则表示网络的恢复自愈能力越差,因此可恢复性指标H可量化为
| $ H = \left\{ \begin{array}{l} 1,\;\;{V_0} \le {V_L}\\ 1 - {e^{ - \left( {\Delta {V_h}/\Delta th} \right)}},\;\;\;\;{V_0} > {V_L} \end{array} \right. $ | (3) |
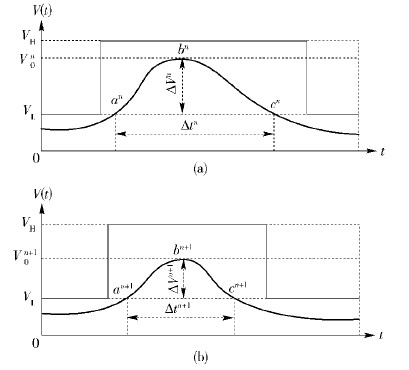
图 4表示两次毁伤事件下的“自适应性状态”,图(a)中曲线an—bn—cn段代表第n次发生毁伤事件Tn时的性能变化情况,图(b)中曲线an+1-bn+1-cn+1段代表第(n+1)次发生毁伤事件Tn+1时的性能变化情况,网络自适应性指标A量化为
| $ A = \left\{ \begin{array}{l} 0,\;\;\;当\Delta {V^n} < \Delta {V^{n + 1}}或\Delta {t^n} < \Delta {t^{n + 1}}时\\ \alpha \frac{{\Delta {V^n} - \Delta {V^{n + 1}}}}{{\Delta {V^n}}} + \beta \frac{{\Delta {t^n} - \Delta {t^{n + 1}}}}{{\Delta {t^n}}},\;\;\;\;其他 \end{array} \right. $ | (4) |
其中α、β为权重系数,且α+β=1.
2.6 网络可生存性综合计算毁伤事件威胁度是指事件发生可能给系统造成的影响程度. 采用等级赋值法对其进行量化,如表 1所示.
| 表1 威胁度等级量化表 |
网络对事件T的应急响应能力R(T)计算为
| $ R\left( T \right) = \varepsilon S + \gamma D + \eta H + \lambda A $ | (5) |
假设事件T的威胁度为WT,则针对事件T的网络可生存性U(T)表示为
| $ U\left( T \right) = R\left( T \right){W_T} $ | (6) |
ε、γ、η和λ为权重系数,且ε+γ+η+λ=1. 若发生了m次事件,则网络总体可生存性U表示为
| $ U = \frac{1}{m}\sum\limits_{i = 1}^m {U\left( {{T_i}} \right)} $ | (7) |
对实验室搭建的局域网络Net-1和Net-2分别进行3次毁伤测试,事件T1:蠕虫攻击;事件T2:链路断开;事件T3:节点故障. 任选两节点安装Netperf,实现网络性能实时监测. 依据监测数据样本对Net-1和Net-2的可生存性进行分析与评估.
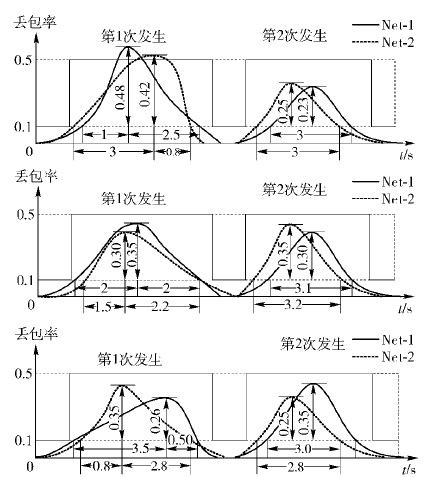
3.1 网络环境及相关参数设置3次毁伤测试事件相关参数如表 2所示,选取丢包率作为性能参量,性能变化曲线如 图 5所示.
| 表2 毁伤事件参数表 |
图 5中横坐标为时间t,纵坐标为丢包率,上下边界值设定为VH=0.5、VL=0.1;设式(4)中系数 α=β=0.5,式(5)中系数ε=γ=η=λ=0.25;指标S、D和H的计算以第1次毁伤事件条件下采集的数据样本为依据,仅在计算指标A时才使用第2次毁伤事件条件下采集的数据样本.
3.2 网络可生存性评估及分析1)网络Net-1可生存性评估
① 事件T1条件下
由式(1)得S=0.778;由式(2)得D=0;由式(3)得H=0.175;由式(4)得A=0.332;由式(5)得R(T1)=0.321;由式(6)得U(T1)=0.225.
② 事件T2条件下
S=0.862;D=0.839;H=0.161;A=0.184;R(T2)=0.511;U(T2)=0.256.
③ 事件T3条件下
S=0.69;D=0.928;H=0.407;A=0;R(T3)=0.506;U(T3)=0.456.
2) 网络Net-2可生存性评估
① 事件T1条件下
S=0.944;D=0;H=0.41;A=0.307;R(T1)=0.415;U(T1)=0.291.
② 事件T2条件下
S=0.69;D=0.818;H=0.128;A=0;R(T2)=0.409; U(T2)=0.204.
③ 事件T3条件下
S=0.345;D=0.644;H=0.112;A=0.254;R(T3)=0.339; U(T3)=0.305.
3) 评估结果分析
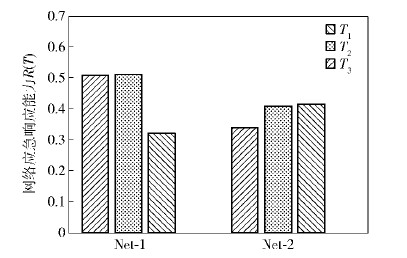
① 网络应急响应能力对比分析
从 图 6可知,事件T1对网络Net-1的毁伤力最大,而事件T3对网络Net-2的毁伤力最大;针对事件T1,Net-2比Net-1具有相对更强的毁伤修复能力;而针对事件T2和T3,Net-1比Net-2具有相对更强的毁伤修复能力.
2) 由式(7)得到网络Net-1的总体可生存性U(Net-1)=0.312,网络Net-2的总体可生存性U(Net-2)=0.267,即U(Net-1)>U(Net-2),说明在突发以上3种毁伤事件条件下,Net-1比Net-2具有更强的生存抗毁能力.
4 结束语先获取网络的性能变化曲线,其次构建网络可生存性评价指标,给出这些指标的量化算法;最后通过综合计算得到网络总体可生存性大小. 实例分析结果表明,所提方法是科学、有效的.
| [1] | Poul E, Kishor S. Trivedi. Network survivability modeling [J]. Computer Networks, 2009, 53(2) : 1215-1234.[引用本文:1] |
| [2] | Zuo Yanjun, Lande S, Pimple M. Analysis and simulation of system survivability [C]//Proceedings of 2010 Seventh International Conference on Information Technology: New Generations(ITNG). Las Vegas: 2010: 36-41.[引用本文:1] |
| [3] | 张乐君, 国林, 张冰, 等. 基于SPN的信息系统生存性分析建模研究 [J]. 计算机研究与发展, 2009, 46(6): 1019-1027. Zhang Lejun, Guo Lin, Zhang Bing, et al. Modeling of information system survivability analysis based on SPN [J]. Journal of Computer Research and Development, 2009, 46(6): 1019- 1027.[引用本文:1] |
| [4] | 伍文, 孟相如, 刘芸江, 等. 基于连续时间Markov的网络可生存性建模与量化 [J]. 吉林大学学报: 工学版, 2013, 43(5): 1395-1400. Wu Wen, Meng Xiangru, Liu Yunjiang, et al. Modeling and quantification of network survivability based on continuous time Markov [J]. Journal of Jilin University: Engineering and Technology Edition, 2013, 43(5): 1395-1400.[引用本文:1] |
| [5] | 陈天平, 孟相如, 崔文岩, 等. 基于网络可生存性态势感知的主动服务漂移模型[J]. 空军工程大学学报: 自然科学版, 2015, 16(6): 76-80. Chen Tianping, Meng Xiangru, Cui Wenyan, et al. A proactive service migration model based on network survivability situation awareness [J]. Journal of Airforce Engineering University: Science edition, 2015, 16(6): 76-80.[引用本文:1] |
| [6] | Ming Liang, Huang Minhuan, Wang Dongxia, et al. Research on survivability metrics based on survivable process of network system [J]. Journal of ACM, 2011, 12(6): 247-250.[引用本文:1] |
| [7] | 伍文, 孟相如, 马志强, 等. 基于组合赋权的网络可生存性模糊综合评估 [J]. 系统工程与电子技术, 2013, 35(4): 786-790. Wu Wen, Meng Xiangru, Ma Zhiqiang, et al. Fuzzy comprehensive evaluation of network survivability based on combinational weight [J]. Systems Engineering and Electronics, 2013, 35(4): 786-790.[引用本文:1] |
| [8] | Ellison R J, Linger R C, Longstaff T, et al. Survivable network system analysis: a case study[J]. IEEE Software, 1999, 16(4): 70-77.[引用本文:1] |