2. 南京邮电大学 计算机学院, 南京 210003;
3. 香港理工大学 计算学系, 香港
传统网络切换仅依赖于数据链路层接收的信号强度.最近的研究尝试综合网络各个层次的信息做出更为智能的决策, 然而这些参数不容易测量和量化.为了找到最优切换策略, 将这些与切换相关的信息分为基本信息、网络信息和用户信息, 并提出了基于模糊逻辑的无线网络切换算法, 以对不同网络层次的参数进行收集、处理和保存, 同时根据这些参数所属类型, 设置不同的权重值来适应不同的应用场景, 以达到良好的环境感知和符合用户个人偏好的智能选择.系统仿真结果显示, 切换准确率和用户期望契合度进一步提高.
2. School of Computer Science and Technology, Nanjing University of Posts and Telecommunications, Nanjing 210003, China;
3. Department of Computing, The Hong Kong Polytechnic University, HongKong, China
The received signal strength is usually used to assist the handover. More metrics from different network layers have been considered to make intelligent handover. However, most of them cannot be easily measured and quantified. The article categorizes the problems as three types: basic, adaptive and action mode. A multi-layer fuzzy logic based algorithm of context-aware handover was proposed to handle all the metrics according to their different types. It is guaranteed that the selected access point can match the users' preference with fewest interactions. Simulations demonstrate that the algorithm can integrate the multi-layer networking metrics to reduce users' interactions effectively.
网络切换是无线网络技术的一个重要研究课题.切换是指移动节点改变当前的网络连接,转换至新的接入网络的过程.在传统的切换中,一般由2个网络边界的相对信号强度(RSS, relative signal strength)来做切换判决.引入了和应用环境相关的参数的切换方式称为智能切换或环境感知切换[1].常用参数包括用户偏好、地理位置、应用类型和资费等.目前的研究主要集中在引入1~2个额外的参数进行量化处理来辅助或者校验现有的切换算法,这虽然比单一用信号强度进行切换判断更为全面,但远远没有达到智能和环境感知的效果.有研究者提出将模糊逻辑算法运用于验证多参数输入无线网络切换算法的正确性[2],目前研究也主要集中在如何通过模糊逻辑算法给出潜在的更优接入节点来辅助传统切换,或者以模糊逻辑算法的结果来判定当前切换策略的准确性.
笔者根据不同网络层的参数对切换的影响,对其进行分类,并赋予其不同的权重,然后进行多层模糊逻辑计算,从而使得切换决策不但考虑了常规物理参数对切换的决定性影响,同时也融合了和用户密切相关的主观因素,这是传统网络切换所不具备的.
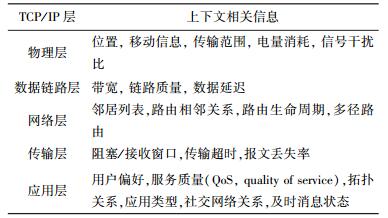
1 基于模糊逻辑的无线网络切换算法1.1 与切换相关的上下文为了实现环境感知的智能切换,必须引入各个网络层与切换相关的参数,即“上下文”. “上下文”在切换过程中,意味着捕捉移动节点和接入点从物理层到应用层的所有相关信息,如终端用户的位置和移动方向、正在运行的应用程序类型、电量消耗以及传统的接入参数带宽、误码率(BER, bit error rate)等,如表 1所示,这些信息获取的渠道包括手机嵌入的传感器元件、应用程序的特征、用户的行为分析.
|
|
表 1 TCP/IP中和切换相关的上下文参数 |
根据实际应用,可以用当前RSS与经验最大值的比值作为信号强度的参考值[3],取值范围变成0~100%. Ahamed等[4]把BER作为信号的另一个考量指标合并到切换算法中. He等[5]提出最少电量消耗切换算法,即寻找最合适的链接使得上行传输的电量消耗最小. Sinky等[6]提出目的地址可以发送基于数据流的切换信息给源地址以切换到质量更好的无线网络中去. Yoo等[7]考虑在简单移动网络模型中建立网络拓扑图,使得网络节点的能量消耗达到最小. Inzerillia等[8]指出移动终端的位置信息可用于获取正在使用的网络与其之间的链路质量数据,并预测用户的行为规律以帮助做出更好的切换决定.
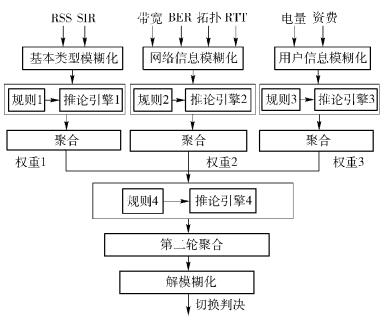
1.2 多层模糊逻辑切换算法整个切换过程可以分为3个阶段:网络选择、切换判定、切换触发.其中网络选择是最为重要的阶段,仅以备选网络的RSS值来做出网络选择决定很容易造成“乒乓”效应.在综合网络选择参数RSS、信号干扰比(SIR, signal to interference ratio)、BER、带宽、网络流量、拓扑关系、能量消耗、资费、用户位置等的基础上,提出了一种多层模糊逻辑切换算法(MLFLH, multi-layer fuzzy logic based handover algorithm),算法流程如图 1所示.
|
图 1 基于模糊逻辑的无线网络选择流程 |
1) 根据切换参数的取值范围、量化标准和对切换的影响程度把所有参数分为3类:第1类是Basic类型,又称基本信息,包括RSS和SIR,因为这2个参数对于当前无线网络切换起到关键作用;第2类是Adaptive类型,又称网络信息,包括带宽、BER、网络流量、拓扑关系和往返时延(RTT, round-trip time)等,它们都会影响切换时的网络选择;第3类是Action Mode类型,又称用户信息,包括电量消耗、网络资费、位置信息和社交网络关系等,这些非客观因素和QoS以及用户感受密切相关.
2) 这3种信息从属于不同的领域,它们之间并没有必然的相互作用关系,但都是影响用户感受的切换因素.目前并没有也不可能找到这些参数之间固定的量化关系,所以采用一种可动态调整的多层模糊逻辑算法来处理这3种信息以做出切换决策.在第一层数据处理中,用3个模糊化过程分别处理这3种类型的数据:第1类基本信息由Basic Fuzzifier处理;第2类网络信息由Adaptive Fuzzifier处理;第3类用户信息由Action Mode Fuzzifier处理.
3) 由于这3种类型的数据处于不同网络层,同时它们对切换的影响也各不相同.根据用户感受,算法对这3个第1层模糊逻辑算法计算的结果分别乘以相应的权值.
4) 在第2层处理中,把3个乘以权值的结果作为输入进行再次的模糊化处理,通过两层模糊逻辑计算之后,最终可以得到模糊切换隶属值,即解模糊化的确切值,值最高的网络节点就是可切换的无线网络.
这样既考虑了传统物理层参数对切换的影响,同时融合了用户主观信息来辅助进行网络选择.
1.3 权重分配原则假设基本信息、网络信息和用户信息的权重分别为x、y和z,显然三者之和为1. z是用户的主观因素,可以通过菜单让用户自行调节.其中最为关键的因素为用电量和资费消耗,其最大阈值不宜超过所有权重的50%.对于一个切换的用户来说,实际通信容量和质量是影响其体验的关键指标,根据香农定理有
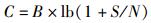
|
(1) |
其中:B为信道带宽,S为信号功率,N为噪声功率,C为信道容量.基本信息中关键指标之一为SIR,即香农定理中的S/N.网络信息中关键指标为信道带宽,即该无线通信方式的理论最大带宽,也就是香农定理中的B.由式(1) 可见,为了取得切换后实际平均带宽的最大化,应该优先增加网络信息的权重y;如果考虑网络稳定性,应该优先考虑信噪比SIR,也就是增大x.有鉴于此,对于基本速率比较高的通信模式,如WiFi和3G以及LTE,由于其基本带宽满足绝大部分用户需求,可以增加x用来选择网络传输稳定性较高的节点;而对于2G等窄带传输,可以增加y来选择网络带宽满足要求的节点.
2 算法执行过程因为与切换相关的参数既有连续数值,又有离散数值,不能给出简单直接的划分.以RSS为例,用户的移动轨迹无法确定,同时也没有一个标准说明备选网络的RSS的强弱,所以首先把所有获取到的输入按照合适的方法进行模糊化.为了简化模糊逻辑的运算过程,把输入和输出模糊集分为3个域:High、Medium和Low,所有输入都得到隶属于相应模糊集的隶属度.所有输入的隶属度值作为模糊规则的前项,同时对这些前项使用模糊操作得到表示评估结果的一个数值.这里对于模糊操作采用概率OR方法,计算方法为
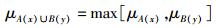
|
(2) |
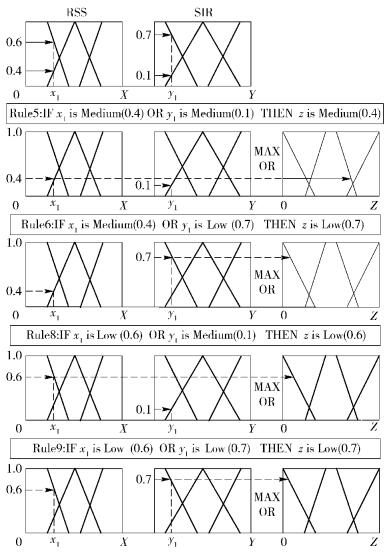
其中μA(x)和μB(y)分别为参数A(x)、B(y)从确切的数值影射到3个模糊集High、Medium和Low的隶属度.以图 2所示RSS的模糊逻辑隶属函数为例:若当前获取RSS的数值与峰值之比x1为43%,这个值分布在Low到Medium区间之内,该值属于Low的隶属度为0.6,属于Medium的隶属度为0.4.隶属度常用的聚合方法包括Mamdani和Sugeno,这里采用Mamdani来进行模糊推理算法,即“并”的方法聚合. 图 2显示了采用Mamdani方法聚合RSS和SIR的全过程.
|
图 2 RSS和SIR的聚合过程 |
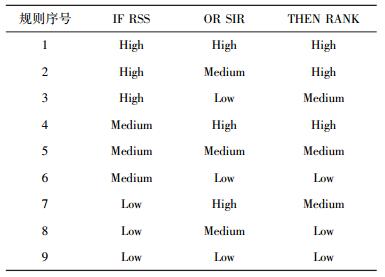
对于以RSS和SIR组合的基本信息,采用IF-OR-THEN规则,即IF RSS is High OR SIR is High THEN RANK is High,ie,Accept. 表 2所示为基本信息的规则列表.
|
|
表 2 基本信息的规则列表 |
与用户感受相关的参数,包括电量消耗、网络资费、位置信息和社交网络关系等,都不是连续的数值,也不可能实时获得.所以也采用IF-OR-THEN规则,由此所有输入之间的矛盾就可以避免了.
根据算法,再将3种数据类型聚合之后的结果依据各自对切换的影响程度或者用户感受度分别乘以相应的权值.在实际运算中,需要保证所有权值之和为1.然后再把这3个已经乘上各自权重的值作为参数,进行第2层的模糊逻辑运算.最终输出是一个解模糊化的精确数值,此处采用Centroid方法来决定使用哪个备选网络进行切换. Centroid方法公式为
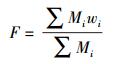
|
(3) |
其中:F为输出的结果,Mi为结果在输出域的隶属度,wi为输出域的范围.
3 算法的性能测评在仿真实验中,平台采用的是Matlab Fuzzy Logic Toolbox.在数据选取时,首先尽量考虑覆盖Basic、Adaptive和Action Mode 3种类型数据;其次,为了显示出用户信息在切换中的作用,测试数据会有所偏重;最后还考虑了WiFi和3G这2种不同的应用场景.本实验主要验证在垂直切换的情况下算法的有效性,也只有在垂直切换中,资费和电量消耗才会有显著的变化.其中,WiFi的资费可以忽略不计,也没有流量或者时间限制;而3G网络正好相反,用户需要为相应服务付出一定的费用.
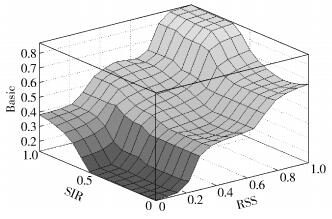
图 3所示为Basic类型的三维输出,水平方向的横轴和纵轴分别表示RSS和SIR的隶属度,垂直方向表示切换的概率.可以看出随着RSS和SIR数值的递增,垂直方向呈平缓上升的趋势,这表明随着信号强度的增强和信噪比的提高,切换的可能性随之提高,这符合传统网络切换的判决标准.对于第3类用户信息,因为网络资费和电量消耗没有明显递减或递增的规律,主要遵循用户个人的偏好,根据实验参数,呈不规则上下起伏型.但仍显示出,当用电量和资费处于最高点时,切换的可能性也降到最低.
|
图 3 MLFLH算法Basic基本信息结果 |
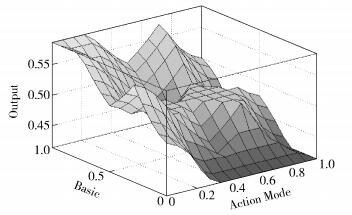
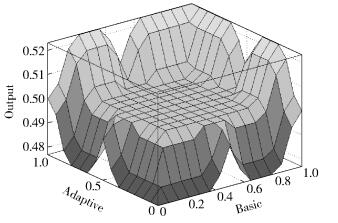
图 4、图 5所示为MLFLH算法的最终结果.由于此时系统有3个输入,1个输出,所以将第3个参数设定成常数来绘制三维输出图,其中图 4以Adaptive类型为常数,图 5以Action Mode类型为常数.常数取值为0,表明切换算法并不受第3个参数的影响,旨在给出其他2个参数取值与切换决策的关系.因为Basic类型不可能取值为0,所以不存在以Basic类型为常数的结果图. 图 4显示,Basic类型的参数起着决定性的作用,但切换决策仍受到Action Mode的影响,由于算法中Action Mode主要考虑影响切换的负面因素,所以,随着Action Mode递增,切换的可能性在递减. 图 5则表明切换概率和Basic及Adaptive的变化趋势一致,当两者到达最高点时切换的可能性最大.
|
图 4 MLFLH算法结果1 |
|
图 5 MLFLH算法结果2 |
由图 3~图 5可知,MLFLH算法进一步提高了命中率,乒乓效应的发生频率明显减少,同时用户的感受也得到体现.例如,当数据中的用户信息权值较高时,虽然备选蜂窝网络的信号状况良好,但是用户敏感的网络资费和耗电量在此时决定了最终结果,实验结果也证实了即便蜂窝网络的信号强度较高,也不执行网络切换.在MLFLH算法中,由于引入了多层模糊算法,带来了一定程度的延迟,但仍在上层应用可接受的范围之内.在情景感知的无线切换中,如果将所有参数逐个量化再考虑对切换的影响,其建模和算法往往相当复杂,每次切换的计算过程会非常耗时,而本算法只是将参数进行模糊处理,从而降低了算法的复杂度、简化了切换的计算过程.
4 结束语在分析网络各个层次和切换相关参数的基础上,提出了基于模糊逻辑的无线网络切换算法.该算法研究了和切换有关的上下文,根据这些参数对切换的影响进行了分类和可变权重的多层模糊逻辑处理.仿真结果表明,模糊逻辑算法可以应用于环境感知的智能切换场景,该算法可以在以物理层参数为基础的前提下综合考虑用户的个人习惯和偏好,从而给用户带来更好的使用体验.进一步的工作包括在移动终端上实现该模糊逻辑算法,来最大程度契合用户期望.
| [1] | Liu Chenggang, Jia Zhenhong, Qin Xizhong, et al. Improvement priority handoff scheme for multi-service wireless mobile networks[J].Journal of Networks, 2014, 9(1): 204–209. |
| [2] | Tripathi N D. Generic adaptive handoff algorithms using fuzzy logic and neural networks[D]. USA: Virginia Polytechnic Institute and State University, 1997. |
| [3] | Atalah K, Macias E, Suarez A. A proactive horizontal handover algorithm based on RSSI supported by a new gradient predictor[J].Ubiquitous Computing and Communication Journal, 2008, 3: 77–88. |
| [4] | Ahmed A, Merghem-Boulahia L, Gaïti D. An intelligent agent-based scheme for vertical hand-over management across heterogeneous networks[J].Annals of Telecommunications-Annales Des Télécommunications, 2011, 66(9-10): 583–602. doi: 10.1007/s12243-010-0235-6 |
| [5] | He Daojing, Chi Caixia, Sammy Chan, et al. A simple and robust vertical handoff algorithm for heterogeneous wireless mobile networks[J].Wireless Personal Communications, 2011, 59(2): 361–373. doi: 10.1007/s11277-010-9922-x |
| [6] | Sinky H, Hamdaoui B. Cross-layer assisted TCP for seamless handoff in heterogeneous mobile wireless systems[C]//Globecom Workshops. [S. l. ]: IEEE, 2013: 4982-4987. |
| [7] | Yoo S J, David Cypher, Nada Golmie. Timely effective handover mechanism in heterogeneous wireless networks[J].Wireless Personal Communications, 2010, 52(3): 449–475. doi: 10.1007/s11277-008-9633-8 |
| [8] | Inzerilli T, Vegni A M, Neri A, et al. A cross-layer location-based approach for mobile-controlled connectivity[J].International Journal of Digital Multimedia Broadcasting, 2011, 201: 1–13. |