文章信息
- 聂莉莎, 蒋滨, 张许, 刘买利
- NIE Li-sha, JIANG Bin, ZHANG Xu, LIU Mai-li
- 基于压缩感知/重采样的NMR噪声抑制新方法
- A Compressed Sensing and Resampling Based Noise Suppression Method for NMR
- 波谱学杂志, 2016, 33(2): 244-256
- Chinese Journal of Magnetic Resonance, 2016, 33(2): 244-256
- http://dx.doi.org/10.11938/cjmr20160207
-
文章历史
收稿日期: 2015-05-04
修订日期: 2016-04-12


DOI:10.11938/cjmr20160207
2. 中国科学院大学, 北京 100049
2. University of Chinese Academic of Sciences, Beijing 100049, China
核磁共振(NMR)波谱分析是分析化学的重要组成部分[1],广泛应用于生物大分子结构,相互作用以及动力学的研究,它已经发展成为结构生物学、代谢组学等热点学科中不可或缺的分析手段[2, 3].然而,与其它谱学分析方法(如质谱)相比,NMR波谱的灵敏度较低,这使得NMR分析需要更多的样品量或者更长的采样时间,才能获得信噪比(SNR)足够的谱图.因此,当样品量很少或者样品不够稳定时,NMR检测就遇到困难.尤其是在蛋白质NMR研究中,由于某些蛋白质的表达量很少或溶解度很低、或浓度高时容易聚集和变性等原因,经常难以获得高SNR的NMR谱图.而且,有些原子核的同位素天然丰度低,导致NMR检测灵敏度低.为了提高观测灵敏度,常用的方法就是将信号进行相干累加,这无疑增加了采样时间.由此可见,发展高灵敏检测方法,力图在较短检测时间内获得SNR足够高的NMR谱图,是NMR波谱学研究的重要领域.
NMR谱图的SNR由信号强度与噪声水平两个因素共同决定,因此,对于NMR波谱分析,提高SNR的途径包括信号增强与噪声抑制两种方式:
(1) NMR信号增强.在其它实验条件相同时,NMR波谱的灵敏度主要取决于核自旋的极化度,即核自旋在不同能级上数目(布居数)之差,通过提高核自旋的极化度可以实现信号增强.此类方法包括:
(a) 采用更高场强的NMR谱仪,通过提高磁场强度(B0)来提高样品中核自旋极化度(ħγB0/2kBT)[4],进而获得更强的NMR信号.
(b) 采用超极化方法提高极化度.通过自旋交换光抽运(SEOP)[5]、动态核极化(DNP)[6]、或者仲氢诱导核极化(PHIP)[7]等超极化手段,将极化度由高极化粒子(如电子)转移至被检测核自旋上,最高可将NMR信号强度提高4个数量级.
(c) 利用NMR脉冲实验提高信号强度.通过设计各种NMR脉冲序列,同样可以提高NMR信号强度,这类方法包括极化转移(如INEPT、DEPT等)[8]、弛豫优化(TROSY)[9]、NOE增强[10]等.该类方法已经得到广泛应用,成为各种异核多维实验(如HSQC、HNCO等)中不可或缺的组成部分[11].
(2) 噪声抑制.与提高信号强度相比,降低噪声水平同样能增强灵敏度,是另外一个提高SNR的有效途径.该类方法包括:
(a) 通过硬件手段降低热噪声水平、提高检测灵敏度.这主要体现在高灵敏NMR探头技术的不断改进和完善,其中最为显著的是使用超低温探头[12],即把接收线圈与前置放大器深度冷却(分别冷却至20 K和80 K左右),以此显著抑制信号检测通路中的热噪声.与相同条件下的常规探头相比,超低温探头可将NMR谱图的SNR提高 3~4倍.
(b) 通过数据后处理方法抑制噪声.窗函数技术[13]就是该类方法中的应用最广泛的典型代表:由于真实信号在NMR采样过程中逐渐衰减,自由感应衰减信号(FID)后段部分以噪声为主,因此将FID与一些函数(如递减指数函数)相乘,就可以有效的放大信号、降低噪声水平、提高SNR.然而,该方法在提高SNR的同时,也增大了谱峰线宽,降低了谱图分辨率.除窗函数之外,最大熵重建(MaxEnt)和去卷积(deconvolution)[14]值法也具备一定的降噪效果,但其实际应用较少,其重要原因之一是计算量大、处理时间较长.然而,随着计算机技术的快速发展,特别是多核心中央处理器(CPU)、图形处理器(GPU)和并行算法的快速发展,逐步突破了大计算量对某些算法的限制瓶颈.
以上各类方法各有其优缺点:配备超低温探头的高场NMR谱仪,目前正装备在越来越多的实验室中,是效果好、普适性高的灵敏度增强方法,但是其购买及维护费用高昂;各类超极化技术虽可将SNR提高几个数量级,但对样品制备有特殊要求,目前尚难广泛应用;各种灵敏度增强的脉冲序列模块,已经成为许多NMR实验中不可缺少的组成部分,但其发展已经高度成熟,获得进一步改善的难度很大.相较而言,数据后处理技术可应用于任何NMR脉冲实验和样品体系中,是一种普适的抑制噪声、提高SNR的方法,并且对谱仪硬件无额外要求,性价比极高.因此,发展噪声抑制的数据处理新方法,是对其它提高SNR方法的有力补充.
前期工作中,我们提出了一种利用统计重采样原理(resampling)进行伪峰、噪声识别与抑制的数据处理方法--NASR[15].发展NASR方法的初衷,是为了抑制多维非均匀采样实验中出现的伪峰.非均匀采样能缩短多维NMR实验时间,但是也会在谱图中引入伪峰,且这些伪峰与采样点分布密切相关[16].重采样是一类统计学习方法,它从原始样本中随机抽取若干子集,通过对这些数据子集的统计分析,得到关于原始样本某些性质的估值[ 17].
NASR引入重采样方法,从原始时域采样数据中随机选取若干数据子集.在这些随机欠采样(undersampled)数据子集重建所得的NMR谱图中,信号峰变化甚小,但伪峰的位置和强度变化剧烈,因此通过统计分析可对伪峰进行有效地识别与抑制.另一方面,由于噪声的随机特性,在随机选取的数据子集中,噪声与非均匀采样伪峰具有相同的性质,因此NASR也可用于噪声抑制,提高SNR.NASR利用重采样方法进行噪声识别与抑制为提高NMR实验信噪比提供了新思路,但是该技术仍然存在如下问题,(1)处理高动态范围谱图时,即谱图中谱峰强度相差悬殊时,容易将弱信号误判为噪声;(2)在利用统计参数识别噪声与信号时,需要进行某些参数调节,处理过程较为复杂,容易引入主观性因素.
因此,要提高NASR重采样噪声抑制的鲁棒性,就需要引入可靠性更高的数据重建算法.研究表明,在低SNR环境下,用压缩感知(CS)实现欠采样数据的谱图重建可靠性高,对高动态范围谱图有很好的重建效果[18].CS是由2006年斯坦福大学Donoho教授、Candès教授和加州大学洛杉矶分校的华裔数学家陶哲轩教授于2006年提出的一种新的信号处理理论[19, 20].CS理论指出,若原始信号是可压缩的(即在某一变换域内是稀疏的),则对原始信号进行随机欠采样后,可通过非线性重建算法以极高概率重建出原始信号.该理论提出后,迅速在信号处理、医疗成像以及无线通讯等领域获得高度关注和广泛应用.2007,Lustig[21]率先将CS理论用于磁共振成像(MRI)中欠采样数据的图像重建.2011年,CS理论开始被用于真实的多维NMR欠采样数据的谱图重建[22, 23].
本文在前期工作的基础上,将NASR与CS技术相结合,发展了NMR数据处理新方法CS_NASR,在实现噪声抑制、提高NMR谱图SNR的同时,排除了主观因素影响,提高了处理结果的鲁棒性.
1 原理 1.1 CS 理论传统的信号采集过程必须满足奈奎斯特(Nyquist)采样定理,即采样频率不能低于信号频谱中最高频率的两倍,但是在信号传输之前,通常会对信号进行压缩处理.传统的压缩技术都是从信号本身的角度出发,通过寻找并剔除数据中隐含的冗余度,实现压缩过程,如图像压缩(JPEG)、视频压缩(MPEG)和音频压缩(MP3)等.但是这种方法是在数据采集之后进行压缩,舍弃了大部分已采集的数据,造成了采样数据的浪费,且计算过程相当复杂.针对这一问题,Donoho教授、Candès教授和陶哲轩教授等人[19, 20]进行了大量研究,从尽可能由少量采集的数据恢复信息的角度,提出了CS理论.CS的核心在于将采样与压缩编码合并进行,采集的是稀疏信号的非自适应线性投影值,可以从远小于Nyquist采样定理所要求的数据量,实现信号的准确或近似重建,缩短采样时间.
CS要实现从少量采集信息重建出大量原始信息需要满足两个条件:首先需要确保这些少量的数据含有原始信号的全局信息;再者通过相应重建算法能够准确的还原原始信息.满足上述条件需要关注以下三个方面:信号的稀疏表示、传感矩阵(获取信号)和重构算法(重建信号).
稀疏表示:信号的稀疏性是CS实现的基础.若一个信号只有少数非零值,那么该信号可称之为自稀疏信号.自然信号几乎都是非自稀疏的,但大多是可压缩信号,可通过相应的稀疏表示转换成稀疏信号.稀疏表示是原始信号的简洁表达,即将信号投影到某种正交变换基,绝大多数变换系数接近零,则原始信号变成了稀疏信号.例如,自然图像的像素值几乎都是非零的,经过小波变换后,绝大多数系数都接近零,即少量的非零值可以表示出原始图像的绝大部分信息.若某些信号不能用正交基进行稀疏表示,还可以采用冗余字典来实现.对于离散时间信号χ∈RN和一组基函数ψ∈RK*N,稀疏性可以表示为:
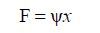 (1)
(1)
其中ψ表示稀疏变换矩阵,如离散余弦变换矩阵、快速傅里叶变换(FFT)矩阵、离散小波变换矩阵、Curvelet矩阵等.如果ψ是一个单位矩阵,这意味着信号x没有进行稀疏变换,这种信号称之为自稀疏信号.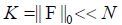

传感矩阵:进行稀疏变换之后,将围绕观测矩阵φ进行压缩采样系统观测部分的设计.观测矩阵的意义在于确定压缩采样得到的M个观测值,保留了原始信号x的全局信息,即保证信号损失最小,确保原始信号能够准确重建.如果信号不是自稀疏信号,则应该结合稀疏变换矩阵,结合后的矩阵称之为传感矩阵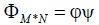
 (2)
(2)
由于观测值的维度M远小于信号的维度N,l0范数最优化问题是一个NP-hard(non-deterministic polynomial-time hard)问题[24],方程(2)式有无穷多个解.理论证明,当信号x是稀疏的或可压缩的,可以用l1范数的最优化来获得l0范数最优化问题的近似解[25].为从M个观测值中精确恢复信号提供了理论保证,观测矩阵必须满足约束等距(RIP)[26, 27]性质.转换成l1范数的方程如下:
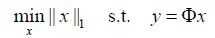 (3)
(3)
Baraniuk已经证明约束等距条件的等价条件是观测矩阵φ和稀疏表示的基ψ不相关[28].所以,CS总是要求相对于观测矩阵进行非相干欠采样.有一些常见的传感矩阵能够满足RIP条件,如加高斯矩阵、一致球测量矩阵、二值随机矩阵、局部傅里叶矩阵和局部哈达玛测量矩阵等[29].
当测量值y包含噪声或考虑重构误差在内的时候,需在方程中加入ε约束条件(ε表示噪声水平).那么,上述问题可以用下式表示(ε>0)[30]:
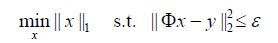 (4)
(4)
将上述有条件约束的凸优化问题,转换为无条件约束的凸优化问题,以拉格朗日增广形式书写如下(λ为拉格朗日乘子):
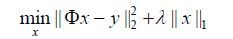 (5)
(5)
因此,重建间接维稀疏采样的NMR谱图,就可以转换成解决如下最优化问题[31]:
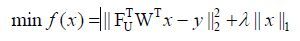 (6)
(6)
其中x是需要被重建的图像;y是观测值(欠采样FID数据);FU表示部分傅里叶变换;W是正交小波变换.由于化学基团的离散性,NMR谱图中大多数信号为自稀疏信号,故本文不需要进行小波变换等稀疏变换.
重构算法:目前已有多种重构算法来求解(6)式,在本文中,我们采用迭代软阈值算法(IST)[18, 32]来求解该最优化问题,因为该算法流程较为简单,易于编程实现.当谱峰高于所设置阈值时,将该谱峰存储到重建谱图之中;然后,对重建谱图进行逆变换得到对应的时域数据,从原始的观测值中减去该时域数据;将余下部分进行小波变换和傅里叶变换后,运用到下一次迭代中去.该重复迭代的过程可以描述为如下形式:
 (7)
(7)
其中,AT由部分傅立叶变换矩阵和小波变换矩阵组成;A表示AT的共轭;y表示观测值;xk表示第k次迭代得到的近似解(第k次迭代得到的重构谱图);是幅值为t的软阈值函数,其中tk随着迭代次数k的增加而递减.在本文中,t设定为每次迭代中最大峰值的90%.
1.2 CS_NASR原理重采样是一类统计学习方法,它从原始样本中随机抽取若干子集,通过对这些数据子集进行统计分析,得到原始数据的统计性质.CS是一类欠采样数据的谱图重建方法,能够从欠采样数据很好地重建谱图.这两点正是CS_NASR能够成功的关键之处.下面将分别进行阐述.
(1) 由NMR原始采样数据随机选取若干数据子集,这些数据的噪声特征是不同的.对于处于频域的NMR谱图来说,每一个信号峰都有其固定频率,即该信号是以固定频率在时域中振荡.而采样数据中的噪声,则产生于NMR谱仪电子线路中各个部件(探头线圈、前置放大器、控制台等)的电子热运动,由于电子热运动的随机性,噪声在采样数据中随机涨落,无固定频率和幅度.因为噪声的随机性,所以在每次扫描所得数据中,噪声特征是不同的.将不同扫描数据累加,由于噪声的随机涨落,叠加起来强度就低于信号叠加起来的强度,从而可以实现SNR增强,这正是常规累加扫描数据获得SNR增强的原理.
同以上类似,将扫描叠加后的时域数据,随机选取为若干子集,那么由于噪声的随机性,在每个数据子集中的噪声特征也是不同的.
(2) CS理论指出,若信号在某一变换域中是稀疏的,则可由对信号的随机欠采样数据中,准确重建出原始信号.对于绝大部分NMR谱图而言,信号是稀疏的,而且,即使在频域中信号不是稀疏的,也能够利用小波变换将其变换到某一稀疏域中处理.因此,毫无疑问,可以利用CS技术由NMR欠采样数据准确重建出谱图,CS的这一特征已经被多次成功应用于NMR和MRI数据处理中.
因此,CS_NASR利用真实信号与噪声的性质差异,实现弱信号与噪声的辨识,从而选择性抑制噪声.即利用重采样方法,随机从原始时域采样数据中选取若干数据子集.由于噪声的随机涨落性质,这些数据子集表现出各自不同的噪声性质.这些欠采样的数据子集可利用CS方法准确重建出噪声不同的NNR谱图.最后,对这些重建所得的多个NMR谱图进行叠加.由于各个谱图信号稳定不变、噪声随机涨落,所得的叠加谱即可实现SNR增强.具体处理步骤分解如下:
(a) 从低SNR的NMR谱图的原始采样数据中,随机选取出若干数据子集.
(b) 这些采样数据子集,实质上就是一系列采样点不同的欠采样数据,利用CS技术将这些欠采样数据重建为若干NMR谱图(欠采样数据子集重建谱).
(c) 将这些欠采样子集重建谱叠加在一起,即获得SNR增强的谱图.
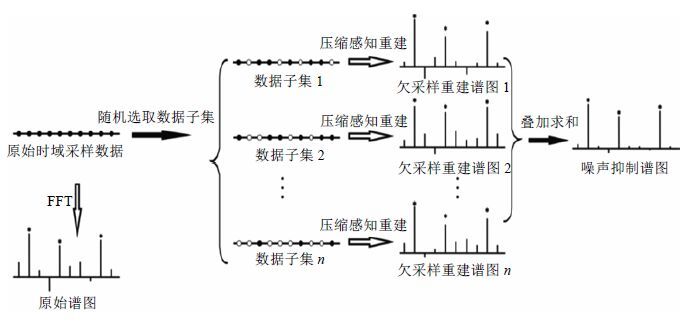
图 1为CS_NASR处理流程示意图.值得注意的是,在本文中,我们是对NMR时域数据采用间接维变密度随机欠采样.众所周知,NMR的能量都集中在时域数据起始的部分,因为信号随着时间的推移呈指数衰减.因此,我们生成一个概率密度函数(PDF),以强调信号起始部分,对后面信号弱噪声强的部分采样更少.然后根据蒙特卡洛算法,我们从已知的PDF,得到采样模式,实现在信号起源部分采样率大,随着时间延长采样率变小.目前的变密度采样模式有多种,我们采用在信号的起始部分均匀采样(即全采样,占所有采样数据的10%),并利用一个指数衰减的加权函数来调制其余部分的随机欠取样.
|
| 图1 CS_NASR 处理流程图 Fig.1 Diagram of CS_NASR processing procedure |
13C NMR谱图具有化学位移范围宽、谱峰线形较窄等特点,因而比1H NMR谱图具有更好的分辨率,但是由于13C核的天然丰度仅为1.1%,且旋磁比(γ)也仅约为1H核的25%,因此13C NMR的灵敏度远低于1H NMR.为获得足够SNR的13C NMR谱图,往往需多次累加,长时间采样.我们选择一维(1D)13C NMR谱图作为CS_NASR的处理对象.本文以5种不同氨基酸混合溶液(Ala和Ser:5 g/L;Phe,Val和Thr:10 g/L)的1D 13C NMR谱图为例,通过设置不同的扫描次数,获得了该样品具有不同SNR的13C NMR谱图:当累加次数足够多时(扫描次数NS= 64),得到高SNR的谱图可明确分辨信号和噪音,在后续对比中作为参照;低SNR谱图(NS= 2)作为CS_NASR方法的处理对象.1D 13C NMR实验在配备了BBO探头的Bruker Avance III 600型NMR谱仪上采集.采用为反门控去偶方式,弛豫等待时间(d1)为5 s,用waltz16对质子去偶,采集点数为16 k.
CS_NASR原理也适用于二维(2D)和更高维的NMR实验.在这里,我们使用了13C和15N同位素双标的泛素蛋白(1 mmol/L,V水∶V重水= 9∶1)的1H-15N HSQC[33]实验为例.HSQC实验广泛应用于分子生物学的研究,如蛋白质动力学与折叠[34]、蛋白质-配体相互作用[35]等.泛素的2D 1H-15N HSQC实验同样在配备了BBO探头的Bruker Avance III 600型NMR谱仪上采集.实验所选择的序列为hsqcgpph,采样期间用garp对13C核去偶.采集点数为t2×t1 = 1 024×64,累加次数NS = 8.通过设置不同的脉冲翻转角以获取具有不同SNR的谱图,即分别采集了翻转角为90°(高SNR)与翻转角为30°(低SNR)的HSQC谱.
1D 13C NMR的CS_NASR处理的过程如下:从低SNR谱图的时域数据中随机抽取了100组数据子集,每组子集仅包含了全部采样点的30%,其中全采样部分占其中的1/3,利用CS对这些数据子集进行谱图重建,得到100个欠采样数据重建谱图.将重建过后的谱图进行叠加,则可得到CS_NASR处理谱.
2D NMR谱的CS_NASR处理过程为:从低SNR谱图的时域数据中随机抽取60组数据子集,每组子集包含全部采样点的30%,利用CS技术对这些数据子集进行谱图重建,得到60个欠采样数据重建谱图,将重建过后的谱图进行叠加,则可得到CS_NASR处理谱.
CS_NASR处理过程用C++语言编程实现,能够与NMR谱图处理软件NMRPipe[36]相结合.在本实验中,相应1D和2D NMR谱图的CS_NASR处理过程分别用时5 min和20 min.
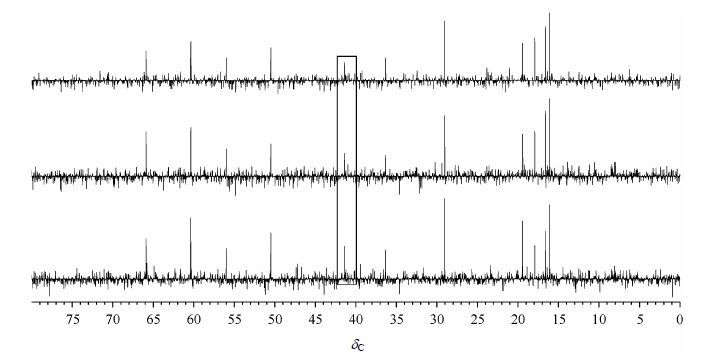
3 结果与讨论图 2随机选取了三个欠采样数据子集CS重建后获得的谱图,这三个谱图中,信号峰大致稳定,而各处的噪声有较大差异,表明CS处理欠采样数据具有较好的鲁棒性,不会带来明显的伪信号.另外,需要指出的是,在这些数据子集重建的谱图中,信号峰的强度略有不同,如图中方框的的信号所示.这是因为噪声也会出现在信号峰所在的位置,这也是每个峰的SNR增加倍数不一样最主要的原因.
|
| 图2 3 个欠采样数据CS 重建谱图 Fig.2 3 CS processed spectra from different undersampling data |
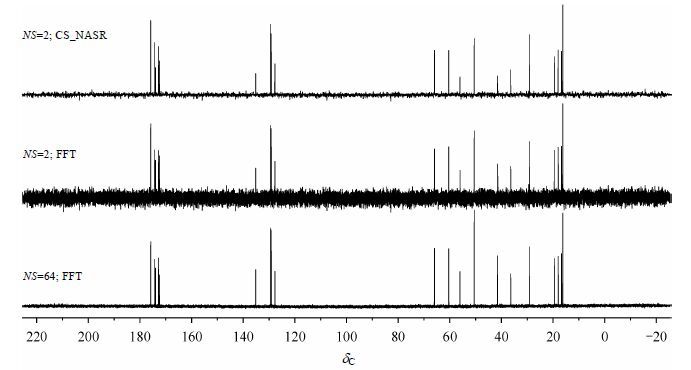
图 3显示了不同方法处理所得氨基酸样品的1D 13C NMR谱.作为参照谱,常规FFT处理的64次扫描获得的谱图,SNR明显较高,采样时间约为70 min;而2次扫描所需采样时间仅约为2.5 min,常规FFT处理该低扫描次数数据所获谱图SNR较低;与常规处理结果相比,同样是2次扫描,采用CS_NASR进行噪声抑制处理后的谱图噪声得到很好的抑制,SNR得到了明显提高.我们计算常规FFT处理谱和CS_NASR处理谱中各个信号的SNR,结果表明,CS_NASR能够使相应谱的SNR提高4.11~41.94倍,平均提高约12.21倍.由于我们采用的是变密度随机采样,具有类似窗函数的功能,所以在CS_NASR的处理过程中,不需要加窗函数.
|
| 图3 5种不同氨基酸混合物重水溶液(Ala和Ser:5 g/L;Phe, Val, Thr:10 g/L)的反门控去耦13C NMR谱.从下到上依次是多次累加信号经常规FFT变换所得的高SNR谱,累加次数NS=64;低累加次数信号经常规FFT变换所得的低SNR谱图,累加次数NS=2;低累加次数信号经CS_NASR处理所得的谱图,累加次数NS=2 Fig.3 Inverse gated decoupling 13C NMR spectra of D2O solution of 5 amino acids mixture (Ala and Ser: 5 g/L; Phe, Val and Thr: 10 g/L). From bottom to top are the normal FFT processed reference spectra with NS=64, the FFT processed noisy spectrum with NS=2, and the CS_NASR processed spectrum with NS=2, respectively |
2D NMR谱图处理结果如图 4所示.同样,具有较高SNR的常规FFT处理的谱图被用作参考谱[图 4(a)],采用低激发角所获取的实验数据作为CS_NASR处理分析对象,采用不同处理方法所获取的谱图分别为图 4(b)(常规FFT处理)和图 4(c)(CS_NASR处理)所示.结果表明,CS_NASR处理过后的谱图[图 4(c)]明显比常规处理所得的谱图[图 4(b)]具有更高的SNR,且信号没有任何明显畸变,更无伪信号出现,证明该方法处理2D NMR谱图时与处理1D NMR谱图一样有效.

|
| 图4 13C、15N同位素双标记的泛素蛋白的1H-15N HSQC谱图.(a) 常规FFT处理的90°激发的HSQC谱(高SNR谱),作为参考谱;(b) 常规FFT处理的小角度激发HSQC谱;(c) CS_NASR处理后的小角度激发HSQC谱,(b)和(c)具有相同显示水平,由于(a)中峰值强度要高得多,所以具有较低的显示水平.2D NMR谱图投影处的1D NMR谱线对应于2D NMR谱图的第372条频域数据(虚线的位置) Fig.4 1H-15N HSQC spectra of 13C, 15N uniform labeled ubiquitin. (a) the normal FFT processed higher SNR spectrum collected with full (90°) excitation. (b) normal FFT and (c) CS_NASR processed spectrum collected with small angle (30°) excitation, respectively. (b) and (c) were plotted in the same contour levels. The contour level of (a) was relatively lower, since the corresponding peak intensities in (a) were much higher. The corresponding 1D spectra above them were slice 372 in the 2D spectra (marked with dashed lines) |
由于采样模式和随机噪声不相同,提取的非均匀采样子谱叠加后,噪声可能会彼此部分抵消,而信号总是累加的,因此CS_NASR数据后处理是一种有效的抑制噪声方法,可以用于一维和多维NMR谱图的处理.使用CS对欠采样数据进行重建,每一个测试谱仍然可能产生一些伪影.如前面所述,不同的采样模式引入不同的非均匀采样伪峰,因此叠加后,非均匀采样带来的伪影也能部分抵消;即使不能抵消,也不影响CS_NASR处理的结果,因为不同位置的伪峰不能进行累加,所以叠加后伪峰的强度远低于信号的强度.这确保了CS_NASR处理结果的准确性.另外,因为在CS_NASR处理过程中,我们直接叠加的测试谱图,以获得SNR更高的NMR谱图.该过程并不需要调整处理参数,因此相比NASR,排除了主观因素对处理结果的影响,提高了处理结果的鲁棒性.
应当注意的是,CS_NASR可以抑制噪声,但处理后的谱图不能反映其信号的真实强度,且信号峰的线型会发生变化,所以CS_NASR处理过后的谱图不能进行定量分析.此外,由于化学基团的离散性,在NMR谱图部分区域没有信号产生,因此大多数化学物质的NMR谱图都具有自稀疏性,故不需要进行稀疏变换.
| [1] | Grant D M, Harris R K. Encyclopedia of Nuclear Magnetic Resonance[M]. Chichester: John Wiley & Sons Ltd., 1996 . |
| [2] | Cavanagh J, Fairbrother W J, III A G P, et al. Protein NMR Spectroscopy:Principles and Practice[M].Second ed. London: Elsevier Academic Press, 2007 . |
| [3] | Bollard M E, Stanley E G, Lindon J C, et al. NMR-based metabonomic approaches for evaluating physiological influences on biofluid composition[J]. NMR in Biomedicine, 2005, 18(3):143–162. |
| [4] | Abragam A. The Principle of Nuclear Magnetism[M]. Oxford: Clarendom, 1961 . |
| [5] | Cherubini A, Bifone A. Hyperpolarised xenon in biology[J]. Prog Nucl Magn Reson Spectrosc, 2003, 42(1, 2):1–30. |
| [6] | Cheng C Y, Han S I. Dynamic nuclear polarization methods in solids and solutions to explore membrane proteins and membrane systems[J]. Annu Rev Phys Chem, 2013, 64(1):507–532. |
| [7] | Green R A, Adams R W, Duckett S B, et al. The theory and practice of hyperpolarization in magnetic resonance using parahydrogen[J]. Prog Nucl Magn Reson Spectrosc, 2012, 67(1):1–48. |
| [8] | Benn R, Gunther H. Modern pulse methods in high-resolution NMR spectroscopy[J]. Angew Chem Int Edit, 1983, 22(5):350–380. |
| [9] | Xu Y Q, Matthews S. TROSY NMR spectroscopy of large soluble proteins[J]. Top Curr Chem, 2013, 335(2):97–119. |
| [10] | Neuhaus D, Williamson M P. The Nuclear Overhauser Effect in Structural and Conformational Analysis[M].2nd Ed. Chichester: John Wiley & Sons Ltd., 2000 . |
| [11] | Sattler M, Schleucher J, Griesinger C. Heteronuclear multidimensional NMR experiments for the structure determination of proteins in solution employing pulsed field gradients[J]. Prog Nucl Magn Reson Spectrosc, 1999, 34(2):93–158. |
| [12] | Kovacs H, Moskau D, Spraul M. Cryogenically cooled probes-A leap in NMR technology[J]. Prog Nucl Magn Reson Spectrosc, 2005, 46(2, 3):131–155. |
| [13] | Lindon J C, Ferrige A G. Digitization and data processing in fourier transform NMR[J]. Prog Nucl Magn Reson Spectrosc, 1980, 14(1):27–66. |
| [14] | Ni F, Levy G C, Scheraga H A. Simultaneous resolution enhancement and noise suppression in NMR signal-processing by combined use of maximum-entropy and fourier self-deconvolution methods[J]. J Magn Reson, 1986, 66(2):385–390. |
| [15] | Jiang B, Luo F, Ding Y, et al. NASR:An effective approach for simultaneous noise and artifact suppression in NMR spectroscopy[J]. Anal Chem, 2013, 85(4):2523–2528. |
| [16] | Kazimierczuk K, Stanek J, Zawadzka-Kazimierczuk A, et al. Random sampling in multidimensional NMR spectroscopy[J]. Prog Nucl Magn Reson Spectrosc, 2010, 57(4):420–434. |
| [17] | Good P. Resampling Methods:A Practical Guide to Data Analysis[M]. Boston: Birkhauser, 2006 . |
| [18] | Bostock M J, Holland D J, Nietlispach D. Compressed sensing reconstruction of undersampled 3D NOESY spectra:Application to large membrane proteins[J]. J Biomol NMR, 2012, 54(1):15–32. |
| [19] | Donoho D L. Compressed sensing[J]. IEEE Trans Inf Theory, 2006, 52(4):1289–1306. |
| [20] | Candes E J, Romberg J, Tao T. Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans Inf Theory, 2006, 52(2):489–509. |
| [21] | Lustig M, Donoho D, Pauly J M. Sparse MRI:The application of compressed sensing for rapid MR imaging[J]. Magn Reson Med, 2007, 58(6):1182–1195. |
| [22] | Holland D J, Bostock M J, Gladden L F, et al. Fast multidimensional NMR spectroscopy using compressed sensing[J]. Angew Chem Int Ed Engl, 2011, 50(29):6548–6551. |
| [23] | Kazimierczuk K, Orekhov V Y. Accelerated NMR spectroscopy by using compressed sensing[J]. Angew Chem Int Ed Engl, 2011, 50(24):5556–5559. |
| [24] | Berlekamp E R, Mceliece R J, Vantilborg H C A. Inherent intractability of certain coding problems[J]. IEEE Trans Inf Theory, 1978, 24(3):384–386. |
| [25] | Chen S S B, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. Siam J Sci Comput, 1998, 20(1):33–61. |
| [26] | Candes E, Romberg J. Sparsity and incoherence in compressive sampling[J]. Inverse Probl, 2007, 23(3):969–985. |
| [27] | Candes E J, Tao T. Decoding by linear programming[J]. IEEE Trans Inf Theory, 2005, 51(12):4203–4215. |
| [28] | Donoho D L. Compressed sensing[J]. IEEE Trans Inf Theory, 2006, 52(4):1289–1306. |
| [29] | Candes E J, Tao T. Near-optimal signal recovery from random projections:Universal encoding strategies?[J]. IEEE Trans Inf Theory, 2006, 52(12):5406–5425. |
| [30] | Donoho D L, Elad M, Temlyakov V N. Stable recovery of sparse overcomplete representations in the presence of noise[J]. IEEE Trans Inf Theory, 2006, 52(1):6–18. |
| [31] | Drori I. Fast l1 minimization by iterative thresholding for multidimensional NMR Spectroscopy[J]. Eurasip J Ad Sig Pr, 2007, 20(1):22–35. |
| [32] | Shrot Y, Frydman L. Compressed sensing and the reconstruction of ultrafast 2D NMR data:Principles and biomolecular applications[J]. J Magn Reson, 2011, 209(2):352–358. |
| [33] | Bodenhausen G, Ruben D J. Natural abundance N-15 NMR by enhanced heteronuclear spectroscopy[J]. Chem Phys Lett, 1980, 69(1):185–189. |
| [34] | Dyson H J, Wright P E. Unfolded proteins and protein folding studied by NMR[J]. Chem Rev, 2004, 104(8):3607–3622. |
| [35] | Shuker S B, Hajduk P J, Meadows R P, et al. Discovering high-affinity ligands for proteins:SAR by NMR[J]. Science, 1996, 274(5292):1531–1534. |
| [36] | Delaglio F, Grzesiek S, Vuister G W, et al. NMR Pipe-A multidimensional spectral processing system based on unix pipes[J]. J Biomol NMR, 1995, 6(3):277–293. |
 2016, Vol. 33
2016, Vol. 33



