2. 成都理工大学, 成都 610059
2. Chengdu University of Technology, Chengdu 610059, China
月球的起源和早期演化,是一个跨学科、跨领域的重大科学问题,月球研究至今,已经获得了海量的数据,如何高效合理的利用这些数据,数值模拟是不可或缺的手段。近年来随着高精度同位素分析技术的提高,超级计算机计算能力和模拟能力的增强,大量新的地月系统组份及同位素数据在不断积累,新的月球形成过程的模拟参数在不断细化,这使得更加深入研究月球形成这一重要事件,并更加清楚认识这一事件对地月系统演化历史的影响成为可能。(林杨挺,2010;欧阳自远和刘建忠,2014)。
月球形成的理论目前有捕获、分裂、共吸积以及大碰撞假说,但这些理论在对地月系统独特性质的解释上,或多或少都存在疑点(Canup and Esposito, 1996;Canup and Ward, 2001,2006;Genda and Abe, 2002,2003,2005;Genda et al., 2007, 2015;Genda and Ikoma, 2008)。表 1详细比较各类月球形成理论的优缺点,从表 1可以看出,大碰撞理论目前除了在氧同位素上尚存疑点,在其他方面都能较好的解释地月系统间的所有约束条件,因此大碰撞理论自确立以来,近几十年一直都是月球形成假说中最被广为接受的一种(Ward and Canup, 2000;Canup and Asphaug, 2001;Melosh et al., 2013)。大碰撞理论的数值模拟工作自理论提出以来,一直都是月球研究的热点,但国内对这方面的工作尚未开展,非常有必要厘清现行的数值模型,相关理论,以及基础认识的研究进展,为以后的工作指明方向(Canup et al., 2001;Canup, 2005, 2010)。
|
|
表 1 月球形成理论的比较 Table 1 A comparison of the Moon formation theories |
大碰撞理论的提出最早可以追溯到1946年,Daly(1946)发文首次提出月球形成于一次大碰撞的观点,但这一理论在当时并没有受到关注。大碰撞假说的再次提出是在1974年,Hartmann和Davis在康奈尔大学举行的一次关于行星的天文研讨会上提出,如果一个足够大的小行星撞击地球,溅射出的地幔物质组成月球,可以满足月球贫挥发分和贫铁核的条件,并可以解释月球密度较低这一观测事实,这一理论在这次会议上也得到了Cameron和Ward的支持,Cameron和Ward还进一步阐明碰撞体的大小应该和火星类似,此后他们分别在1975年和1976年发表论文论述了这一观点,这被普遍认为是大碰撞理论形成的开端(Hartmann and Davis, 1975;Cameron and Ward, 1976)。但大碰撞理论并没有很快被广为接受。此后随着越来越多的阿波罗样品及月球陨石样品出现,并伴随着分析测试技术的进步,新的数据逐渐越来越支持大碰撞理论。直至1984年在夏威夷举行的第一次月球起源重大国际会议上,月球形成的大碰撞理论才得以真正确立,并成为月球形成理论中最被广为接受的一种。此后在1998年蒙特利和2013年伦敦举行的第二次、第三次月球起源重大国际会议上,虽然大碰撞理论受到诸如同位素制约等问题的挑战,但普遍的观点认为,大碰撞理论仍然是目前能够解释地月系统诸多特性的最好的理论(Ida,1997;Ward and Canup, 2000;Canup and Asphaug, 2001;ćuk and Stewart, 2012;Reufer et al., 2012;Melosh et al., 2013)。
在1974年大碰撞理论被重新提出以后,大碰撞过程的定量化研究工作就没有停止过,如Cameron和Ward,Melosh和Sonett,Stevenson等,但这些早期的定量化工作都局限于宏观因素的探讨。真正意义上的数值模拟始于1984年的第一次月球起源的重大国际会议,Kipp & Melosh采用基于传统欧拉网格的CTH方法对大碰撞过程进行模拟,但在当时这一方法显然无法处理大碰撞这一复杂过程,Benz & Cameron则首先采用了一种1977年由Lucy提出的名为光滑粒子流体动力学(Smoothed particle hydrodynamic,简称SPH)的方法,SPH方法具有自适应性、无网格性和粒子形式,非常适宜处理大变形和冲击载荷问题,此后几十年时间里,SPH方法成为大碰撞数值模拟的主要方法(Kipp and Melosh, 1986;Benz et al., 1986)。但受到了计算能力和模拟算法的制约,模型尚无法展示准确的细节和结果。第一个被大家所接受的数值模型由Canup和Asphaug于2001年建立(Canup and Asphaug, 2001),该模型在一个较为宽松的初始条件下,在当时被认为可以解释所有的地月系统特征,这一模型被称为标准碰撞(Canonical impacts)模型。但很快大家发现标准碰撞模型无法解释地月系统间的同位素近似问题,因此此后大碰撞模型的研究工作主要集中于两方面,一方面发展出新的数值模型来代替标准碰撞模型,比较成功的有高自旋地球碰撞(Fast-spinning earth impact)模型,对称地球碰撞(Half-earth impact)模型,以及碰撞-逃逸(Hit-and-run)模型和碰撞前旋转(Pre-impact rotation)模型等(Canup, 2008, 2012;ćuk and Stewart, 2012;Reufer et al., 2012),但这些新的数值模型也都存在各自的缺点;另一方面的工作集中于建立新的理论来弥补现有数值模型的缺陷,比较成功的理论有行星-吸积盘平衡(Planet-disc equilibration)理论,出差共振(Evection resonance)理论(Pahlevan and Stevenson, 2007;ćuk and Stewart, 2012),但这些理论目前尚存一定争议。总体而言,目前的大碰撞的数值模型和理论还不能完全解释月球形成的机制,对大碰撞理论的各种约束条件和过程机理还需要更深入的研究和探讨(Agnor et al., 1999;Barr and Canup, 2008,2010;Barr et al., 2010)。
2 大碰撞理论的数值模拟方法简介目前大碰撞理论的最主要模拟方法为SPH(光滑粒子流体动力学)方法。此外,随着近年来计算技术的飞速发展,AMR-CTH等方法也得到一些应用(Crawford et al., 2006;Citron et al., 2015)。
2.1 SPH方法简介SPH方法是一种无网格、自适应、具有拉格朗日性质的动力学求解方法,方法的实质是利用一组任意分布的粒子来对偏微分方程的求解域进行离散化,再利用离散点来构造近似函数,从而将偏微分方程转化为一系列离散化、只与时间有关的常微分方程,最后通过传统的数值解法求解这些常微分方程。SPH方法核心的2个步骤就是核函数近似过程和粒子近似过程(Yonezawa et al., 2003;Nakajima et al., 2007)。
2.1.1 核函数近似过程对于任意函数f(x),都可以采用如下定义的积分表达式:
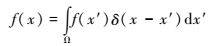
|
(1) |
式中:f是变量x的任意函数;Ω是包含x的积分域;δ(x-x′)是狄拉克δ函数。如果采用函数W(x-x′,h)取代式(1) 中的狄拉克δ函数,则f(x)的积分表达式可以写为:
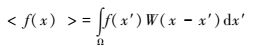
|
(2) |
式中:W称为光滑函数(Smoothing function)或者核函数(Kernel function);h是定义光滑函数W的影响区域的光滑长度。由于核函数W不是狄拉克δ函数,所以式(2) 的积分表达式不是精确的,只是一种近似表达。
2.2.2 粒子近似过程使用粒子体积ΔVj取代积分近似式中粒子j处无穷小的体积元dx′,那么核函数近似的积分表示式可以进一步写成离散化的粒子近似式:
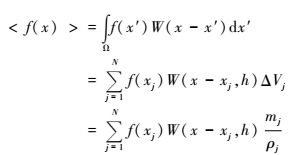
|
(3) |
因此,在粒子i处的函数值f(xi)的SPH粒子近似式为:
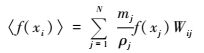
|
(4) |
式(4) 说明粒子i的函数值可以由i粒子的紧支域内所有粒子的函数值乘以各自的质量并除以各自的密度,然后加权核函数求和得到。
在粒子i处的函数导数∇·f(x)的SPH粒子近似式可以写为:
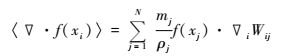
|
(5) |
式(4) 和式(5) 的意义在于将场函数及其导数的连续积分表达式转化为了在任意分布的粒子上的离散化求和表达式,这使得SPH方法的数值积分无需任何背景网格。
2.2.3 连续介质力学基本守恒方程的SPH公式采用SPH法对连续介质力学基本守恒方程(Navier-Stokes)在空间域上进行离散近似,考虑人工黏性Πij和人工热流Hi的影响,连续介质流体力学控制方程的SPH公式如下:
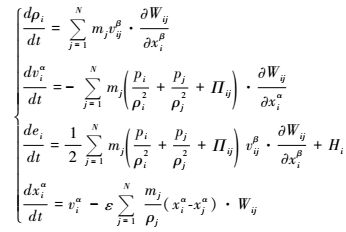
|
(6) |
其中,p为静水压力,x是空间位置矢量,v是速度矢量,上标α和β是空间坐标的方向,ρ是密度,e是内能,t是时间,ε是人工压缩率,m为粒子质量,N为紧支域内粒子数量,W为核函数。
2.2 AMR-CTH方法SPH方法的优点主要是采用粒子而非传统的网格方法来计算导数,避免了由于网格划分产生的一系列问题,如易于跟踪每个流体粒子的轨迹而得到整个流场的变化规律,在大空间数值模拟时可以有效节约计算内存和时间等。但SPH方法由于在核近似和压力求解方法上存在天然的弱点,因此其精度不足。Wada等(2006)认为SPH模型并不能很好的处理大碰撞后的吸积过程,一是由于SPH方法是基于Lagrangian描述的,对于扩散区域它的分辨率不够,尤其是对于吸积盘来说,粒子数只有全部粒子的百分之几,很难得到准确的吸积盘结构;二是在SPH方法中,空间分辨率是由核函数控制的,对于处于扩散区域的吸积盘,核函数的半径甚至可以大到和吸积盘一样大,这会导致月球的吸积时间变得很短,会产生误差。
因此,一些研究者(Kipp and Melosh, 1989;Wada et al., 2006;Crawford and Kipp, 2010;Canup et al., 2013)尝试采用基于欧拉网格的方法(CTH、AMR-CTH)对大碰撞理论进行模拟。CTH最初是由美国Sandia国家实验室开发的用于处理大变形和爆炸冲击问题的一组代码,为了模拟大碰撞过程,后期增加了并行N-body引力计算,M-ANEOS状态方程,以及自适应网格加密(AMR)算法,改进后的方法被称为AMR-CTH方法。相比SPH方法,AMR-CTH方法具有更好的精度,但其算法更加的复杂,也会极大的增加计算量。受制于计算能力,早期基于欧拉网格的大碰撞模拟主要起到方法探索的作用,一些工作的结果也并不完整,直至2013年Canup和Barr的工作才具备实际意义。
据Canup和Barr在2013年的结果,在碰撞开始的几个小时之内,AMR-CTH的结果和SPH的结果基本一致;在碰撞开始后5~10 h的时间范围内,二者的结果才出现了一些差异;经过25~50个小时以后,2种方法得到的最终结果之差在10%以内。但不能认为这10%的误差完全由SPH方法造成,因为AMR-CTH方法的网格划分有一定范围,对于大碰撞这样一个发散的系统,物质一旦离开网格范围,AMR-CTH方法便难以追踪,这也会导致误差的产生。总体而言,Canup和Barr认为AMR-CTH方法的引入并未对大碰撞的模拟结果带来重大的影响。但Asphaug认为仅仅因为AMR-CTH方法和SPH方法运行结果比较接近,并不能认为SPH方法没有问题,一些基于欧拉网格法的结果中吸积盘存在强烈的冲击振荡,这可会能让吸积盘崩溃,但在SPH方法中并未出现这一现象(Asphaug,2014)。
目前来看,AMR-CTH方法并未对SPH的模拟结果产生大的挑战,SPH方法仍然是目前在大碰撞领域最常用的模拟方法。但基于AMR-CTH方法在数学理论上的完备性,随着未来计算能力的不断拓展,AMR-CTH方法存在更广阔的应用前景。
3 主要的大碰撞数值模型及制约因素在讨论现行的大碰撞数值模型以前,必须明确地月系统间的一些基本观测事实和约束条件,这是研究大碰撞数值模型的基础(Shukolyukov and Lugmair,1998;Shukolyukov et al.,1998;Shearer et al.,2006;Ward and Canup,2006a,2006b,2010)。
(1) 月球的密度(3.34 g/cm3)低于地球(4.2 g/cm3)及其他内太阳系行星,这意味这月球没有铁核或者只有很小的铁核(<5%);
(2) 月球具有很大的质量和角动量,月球与地球的质量比达到1 ︰ 81.3,而其他类似的卫星与类地行星质量比一般都小于1 ︰ 1000,并且月球携带了现今地月系统大部分的角动量;
(3) 地球与月球的间距在不断增加;
(4) 月球的形成时间非常晚(至少晚于太阳系形成后30 Ma),这一时间远远晚于与月球类似的其他星胚;
(5) 许多证据表明月球经历过全月性的熔融(岩浆洋)事件,相比地球,月球的中等挥发性元素(K、Pb、Bi等)严重缺失;
(6) 许多难熔性元素的同位素组成在地月系统间一致,而在太阳系其他物种间组成截然不同。
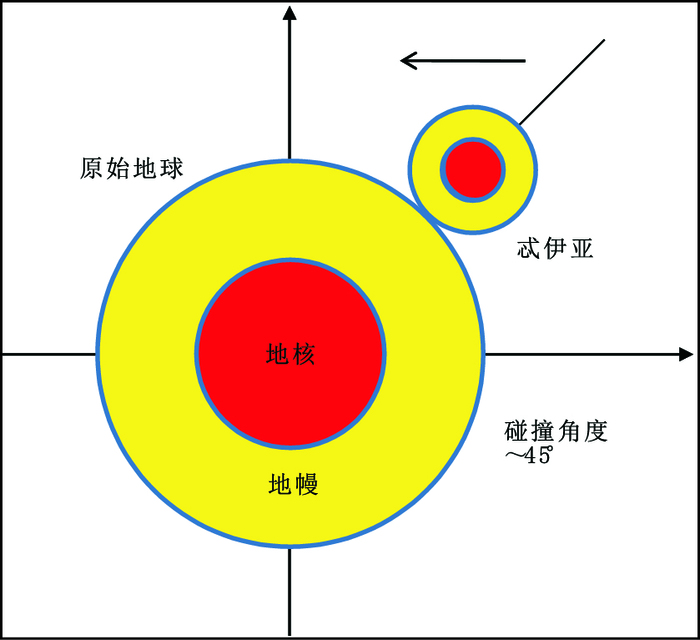
3.1 标准碰撞(Canonical impacts)模型及同位素制约标准碰撞模型由Canup和Asphaug于2001年建立,并于2004年对模型的状态方程进行了修正(Canup and Asphaug, 2001;Canup,2004)。依据标准碰撞模型的运行结果,月球形成于一次低速,碰撞速度vimp~1.0-1.1vesc(vesc为地球逃逸速度,值为11.2 km/s),碰撞体质量约为火星大小[0.1<γ<0.15, γ=Mi/(Mi+Mt)],碰撞角度约为45°(b~0.7) 的一次碰撞。碰撞完成以后,吸积盘与原始地球的总角动量L与现今地月系统角动量LEM比较接近,至多为L≤1.2LEM,吸积盘的温度为3000~4000 K,吸积盘的质量至多为现今月球质量的两倍(MD≤2ML)。依据模拟的结果,碰撞体的铁核几乎全部被原始地球所吸收,且吸积盘中的物质绝大部分(>80%)来源于碰撞体。图 1为标准碰撞模型的最优结果示意图。
|
图 1 标准碰撞模型示意图 Figure 1 A sketch of the canonical impact model |
标准碰撞模型提出以后,最初被认为几乎解决了所有的月球形成问题。吸积盘中的物质绝大部分来源于碰撞体,只有很少一部分来源于原始地球地幔,这一结果最早也被认为是解释月球富FeO的一个证据,但这一认识成为标准碰撞模型的最大弱点。随着高精度同位素分析技术的发展,一系列同位素数据对标准碰撞模型提出了强烈的挑战。同位素问题是由Wiechert等(2001)正式提出,但事实上陨石及天体化学界早已知道这一事实,即火星SNC陨石的三氧同位素组成(Δ17O)与地球之间存在显著的偏差(之前这一偏差被分析精度的误差所掩盖),且这一偏差在太阳系内不同物种间普遍存在。但地球和月球的三氧同位素组成仍然保持一致,这意味月球物质不可能主要来源于碰撞体。
地球和月球之间的同位素制约并不仅仅发生在氧同位素上。早在1995年,Humayun和Clayton就指出39K/41K含量在地球和月球之间基本相同(,Humayun and Clayton, 1995a,1995b),Lugmair和Shukolyukov(1998)发现地球和月球的53Mn—53 Cr组成也非常相似,2007年地球和月球的同位素近似问题扩大到28Si,29Si,30Si与182W/184W,其中182W/184W的偏差略微超出了检测限,但与太阳系内其他物种之间的差距相比,这一偏差微乎其微(Georg et al., 2007;Touboul et al., 2007)。Zhang等(2012)研究发现难熔元素47Ti/50Ti在地球与月球之间也基本一致。总体而言,标准碰撞模型已经受到越来越多地月系统间同位素组成的挑战。
在这些同位素制约当中,最严格的约束来源于氧同位素,同时太阳系不同物种间的各种同位素组成中,氧同位素的研究也是最全面最彻底的。Canup构造了|δfT|用于表征碰撞后吸积盘与地球间的组份差异(|δfT|=0表明地月组成一致),假设碰撞体的物质组份及同位素组成类似于火星的情况下,Δ17O对|δfT|值的要求为|δfT|<2%,而相应47Ti/50Ti对|δfT|值的要求为|δfT|<10%,53 Cr对|δfT|值的要求为|δfT|<42%。当然,实际上碰撞体的物质组份是未知的,考虑碰撞体物质组分的可能波动范围,以及后期可能的混合改造因素,大碰撞模型对| δfT|值的要求可以放宽至| δfT|<15%的范围。在后续的研究中,|δfT|逐渐成为衡量地月系统间组分与同位素差异的常用指标(Canup, 2008, 2012)。
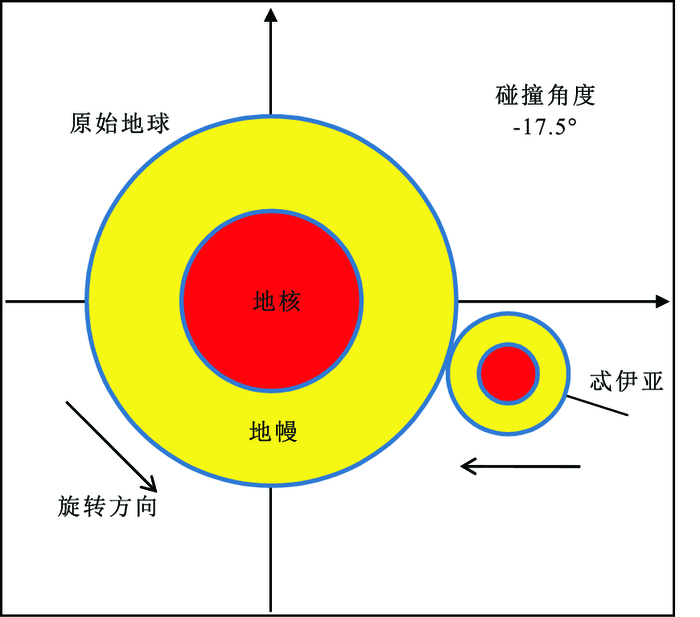
3.2 高自旋地球碰撞(Fast-spinning Earth impact)模型及角动量制约由于标准碰撞模型无法满足大碰撞模型的同位素制约,一些新的数值模型被提出。ć uk和Stewart于2012年建立了高自旋地球碰撞模型,这一模型相对标准碰撞模型而言,碰撞体质量更小(Mi=0.03~0.1M⊕),碰撞速度更大(1.5≤vi/vesc≤2.5),碰撞角度更小(b~-0.3),同时原始地球具有非常高的自旋速度(自旋周期T为2.3~2.7 h,达到原始地球分裂速率的30%)。碰撞完成以后,高自旋地球碰撞模型产生了一个相比标准碰撞模型质量略大(1.8~2.6ML)的吸积盘,吸积盘的物质主要来源于原始地球的地幔,吸积盘|δfT|值范围为6%~15%,系统总角动量值L为1.9~2.8LEM之间。图 2为高自旋地球碰撞模型的最优结果示意图(ćuk and Stewart, 2012)。
|
图 2 高自旋地球碰撞模型示意图 Figure 2 A sketch of the fast-spinning earth impact |
Asphaug(2014)认为这一碰撞模型的实质是一个小型碰撞体撞击了高自旋的原始地球,触发了原始地球分裂,分裂的地幔物质形成了月球。由于组成月球的物质绝大部分来源于原始地球,所以该模型能够满足地月系统的同位素制约,但它最终会产生过剩的角动量(总角动量L为1.9~2.8LEM),这与现今的地月系统角动量不符。学界普遍认为大碰撞事件完成以后,地球的自转周期约为5 h,此后由于地月间的潮汐作用,地球的角动量传递至月球,使得地球的自转周期逐渐增加到现今的24 h,而月球的与地球的间距也逐渐增加,由~2.9RE增加到现今的~60.3RE。这一过程中,地月系统间的角动量将保持守恒,在潮汐作用中海洋与洋底的摩擦会损失一些能量,但这一损失对地月系统角动量的影响不超过10%,大碰撞事件后,地月系统理想的总角动量约为1.1LEM。高自旋地球碰撞模型中总角动量L为1.9~2.8LEM,角动量显然是过剩的,这成为高自旋地球碰撞模型的最大挑战。此外这一模型还需要解释原始地球的高初始自旋速度。
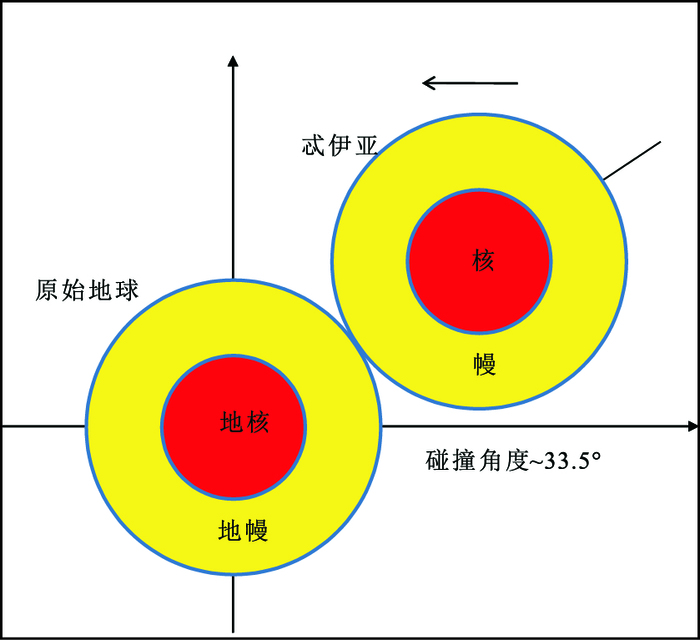
3.3 对称地球碰撞(Half-earth impact)模型及角动量制约对称地球碰撞模型由Canup在2012年建立,模型的思想是如果碰撞体足够大,大到足以对原始地球的组分产生显著的影响,那即使最后碰撞形成吸积盘的物质组成中包含了很多碰撞体的物质,吸积盘与原始地球之间仍然可能具有近似的同位素组成(Canup,2012)。一种极端的情况是碰撞体与原始地球质量完全一致(γ=0.5),并经历了一次完全对称的碰撞,那最终形成的吸积盘与碰撞后原始地球将具有完全一致的同位素组成,相应|δfT|=0。对称地球碰撞模型的初始参数有一个较为宽松的范围,碰撞体质量与原始地球接近(0.4≤γ≤0.5,γ=Mi/(Mi+Mt)),碰撞速度为1≤vi/vesc≤1.6,碰撞角度为0.35≤b≤0.7。模型运行最终的|δfT |范围为0.3%~15%,同样可以产生一个最终组份近似的原始地球与吸积盘,该模型产生的吸积盘的质量为1.7~5.5ML,对称地球碰撞模型也产生了过剩的角动量,系统总角动量L为1.8~2.7LEM(图 3)。
|
图 3 对称地球碰撞模型示意图 Figure 3 A sketch of the half-earth impact |
对称地球碰撞模型的优点在于这一事件发生的概率比其他模型更大,Canup认为在行星形成演化的最后阶段,2个质量相当的星子(0.4≤γ≤0.5) 发生碰撞的概率较高,而一个较小的星子与一个较大的星子(γ~0.1) 发生碰撞的概率较低(Canup,2012)。Raymond等(2009)的模拟实验也表明了在行星演化最后阶段,γ=0.46的星子间发生碰撞概率可以达到10%。
对称地球碰撞模型产生的吸积盘质量略微偏高,为1.7~5.5ML,但由于该模型产生的吸积盘形成温度更高,吸积盘中包含了50%~90%的气态物质,Canup(2012)通过对吸积模型研究,认为这一情况不会影响月球的形成。对称地球碰撞模型的主要缺陷还是来源于角动量过剩,这一模型最终的总角动量为1.8~2.7LEM,这与现实的观测情况也是不符的,此外该模型的碰撞能量巨大,对后期地月系统的影响还需要进一步研究探讨。由于对称地球碰撞模型和高自旋地球碰撞模型产生的角动量和能量都较大,有些文献中把这2个模型统称高角动量(High-angular-momentum)模型或者高能(High-energy)碰撞模型,本文沿用前一说法。
3.4 其他模型及存在问题除了标准碰撞模型和高角动量模型以外,还有一些数值模型也被提出,但在影响力上比上述3个模型稍低。
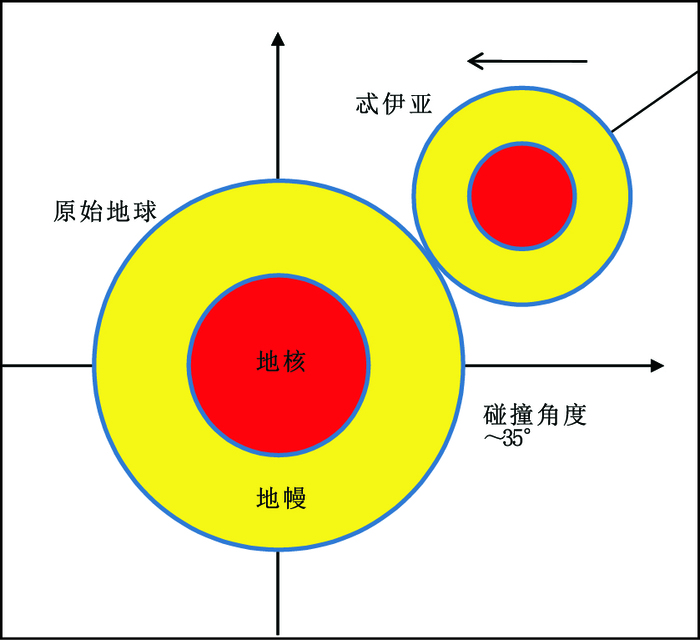
Reufer等(2012)提出了碰撞逃逸(Hit-and-run)模型。相比标准碰撞模型,成功的碰撞逃逸模型的碰撞速度vi稍快,为1.2~1.25Vesc,碰撞角度更小,为32.5°~40°,碰撞体质量略大γ~0.18。在碰撞逃逸模型中,碰撞体的一部分物质最终离开了地月系统,这部分物质带走了一些角动量,但这一模型的角动量仍然略微偏高。即使在碰撞逃逸模型的最优结果中,最终的δfT值为-35%~ -37%,最终的地月系统角动量为1.28LEM,均不完全符合要求,碰撞逃逸模型在地月系统同位素组成和角动量上均存在缺陷。另外Asphaug还认为逃逸的部分碰撞体物质可能会重新被地球所吸引(Asphaug,2014)。碰撞逃逸模型的最优运行结果如图 4所示:
|
图 4 碰撞逃逸模型示意图 Figure 4 A sketch of the hit-and-run impact |
Canup(2008)在标准碰撞模型被质疑以后,尝试修正标准碰撞模型,建立了碰撞前旋转(Pre-impact rotation)模型。在标准碰撞模型中原始地球和碰撞体都是没有自旋的,但在行星形成晚期,二者可能具有很强的自旋,Canup将自旋角动量加入到模型中。模拟结果表明,是否增加自旋角动量,对碰撞速度、碰撞角度和吸积盘质量都没有产生影响,不同之处在于碰撞体的质量会增加到原始地球质量的20%,碰撞过后总角动量为L~1.1LEM,角动量结果相比标准碰撞模型更优。然而,该模型吸积盘的物质主要仍然来源于碰撞体,即使将参数(LS,Li,γ,ξ)调整到极限,仍然无法满足地球和月球的同位素制约。总体而言,碰撞前旋转模型可以看成是标准碰撞模型的一种修正。
4 大碰撞模型的相关理论由于现行的大碰撞数值模型存在各自的缺陷,一些新的理论开始提出来弥补这些缺陷,试图通过两步的方式建立月球的形成理论。其中比较有影响力的理论有行星-吸积盘平衡(Planet-disc equilibration)理论和出差共振(Evection resonance)理论。
4.1 行星-吸积盘平衡(Planet-disc equilibration)理论在标准碰撞模型受到同位素制约的挑战以后,大家开始思考碰撞后原始地球与吸积盘之间同位素平衡问题。Pahlevan和Stevenson(2007)提出开创性的行星-吸积盘平衡理论,从全新的角度来解释了地月系统的同位素近似问题。
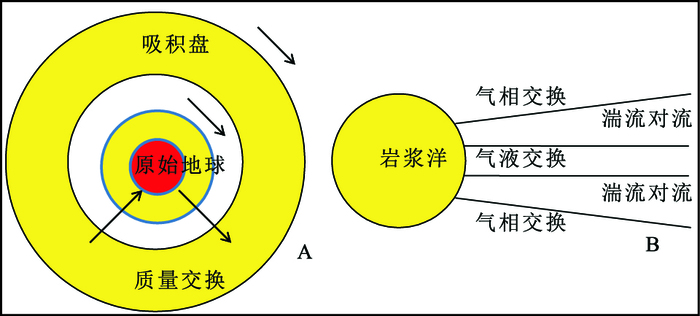
行星-吸积盘平衡理论认为大碰撞过后,地月系统会经历大范围的熔融和部分的气化,湍流对流作用使得原始地球硅酸盐的气体部分会与大碰撞形成的吸积盘的气体部分发生混合,使得吸积盘与原始地球的地幔之间发生物质交换,从而达到同位素组份的平衡,如图 5所示。这一理论如果成立,可以使得大碰撞事件彻底摆脱地月系统间的同位素制约,然而这一理论目前也存在很大的争议。
|
图 5 Planet-disc equilibration理论示意图 Figure 5 A sketch of the planet-disc equilibration theory |
依据估算,要让原始地球与吸积盘之间产生充分的物质交换,这一平衡过程至少要持续100~1000年的时间(Pahlevan and Stevenson, 2007)。而过去的标准吸积模型中月球的吸积形成时间至多为1年,因此行星-吸积盘平衡理论需要重新修正月球的吸积模型,延长吸积时间。最新的月球吸积模型允许月球吸积时间达到120年左右,然而,正是同一模型表明外吸积盘的物质会很快冷却(小于一年),这会使得外吸积盘不再发生物质交换,从而保留较多的碰撞体部分物质(可能会损失一些挥发分),即使按照新的吸积模型,它仍然不能完全解决现今地月系统间的同位素一致问题。
按照Melosh的估算(Melosh et al., 2013),原始地球与吸积盘之间要产生充分的物质交换并达到同位素组份平衡,两者间交换的物质的量大约为整个吸积盘质量的4.6倍,如此大规模的物质交换,必然在原始地球与吸积盘之间产生巨大的角动量交换,这将会使得吸积盘无法维持在自身的轨道上运转。
这一模式的另外一个问题在于能否解释诸如TiO2等难挥发元素在地月间的组份一致与同位素一致(Zhang et al., 2012),Pahlevan和Stevenson估算采用的温度约为3000 K,在这一温度下,TiO2的气体浓度非常低,即使吸积盘能够存在100年以上的时间,在这一时间范围内也很难让TiO2等难挥发元素也能通过气相物质充分交换而达到同位素组分平衡。
原始地球与吸积盘通过充分的物质交换达到了同位素组份平衡,但二者的挥发性元素在这一过程中却没有达到平衡。同位素组分平衡与挥发性元素组分平衡间存在矛盾。
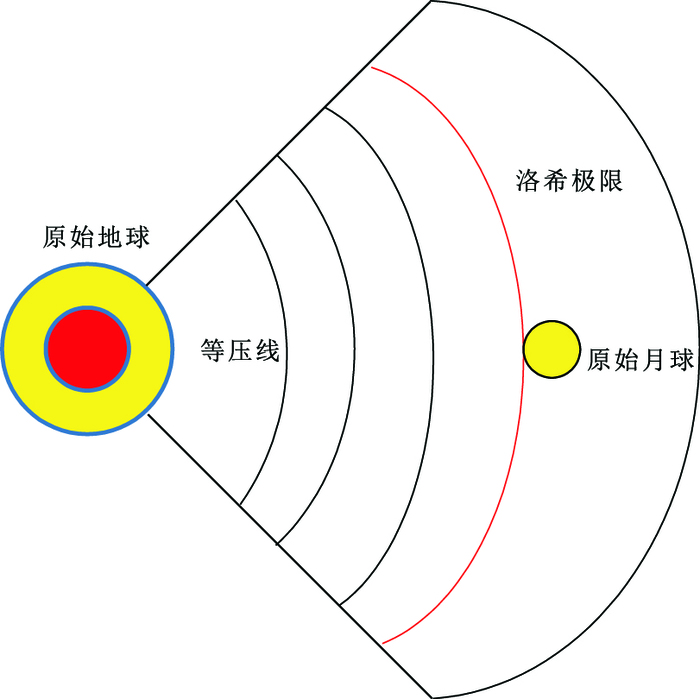
行星-吸积盘平衡理论在2016年又有了新的进展,Lock等(2016)提出了新的认识,认为近年的高角动量模型由于其高能碰撞属性,会导致原始地球进入一个HSSL(hot spin stability limit)的状态,这会将原始地球硅酸盐与吸积盘发生气(液)相混合的范围扩展至洛希极限以外,而月球将直接在这个范围内吸积形成,如图 6所示。这一新的理论能够解释行星-吸积盘平衡理论现存的所有缺陷,但这一新的理论尚未正式发表,因此还不清楚其计算细节,需要密切追踪这一理论的新动态。不过这一理论在解释具体的大碰撞数值模型上还是有一定的局限性,它不能解释标准碰撞模型的同位素制约问题,因为标准碰撞模型的碰撞能量不足,高角动量模型的碰撞能量充分,但目前的高角动量模型已经可以满足地月系统的同位素制约。但无论如何,这一新理论都可以极大的放松数值模型的同位素制约。
|
图 6 新Planet-disc equilibration理论示意图 Figure 6 A sketch of the new planet-disc equilibration theory |
行星与吸积盘平衡理论的实质在于建立了大碰撞事件发生以后,原始地球与吸积盘的组分再平衡模型。它的意义在于,成功的行星吸积盘平衡理论能够弥补标准碰撞模型存在的缺陷,即使这一再平衡作用是不完全的,它仍然会对现行大碰撞数值模型产生重要的影响。
4.2 出差共振(Evection resonance)理论高角动量的2个模型能够解释地月系统间的系列同位素近似的情形,但它们的模拟结果均会产生较大的角动量,与笔者现在观测到的地月系统角动量LEM不符合。ć uk和Stewart(2012)在建立高自旋地球碰撞模型时就提出了出差共振理论,出差共振是太阳、地球与月亮间3体运动,发生在当月球轨道近地点的进动周期与地球轨道完全耦合时,他们认为如果新生成的月球能够被太阳捕获而发生出差共振运动,那么有可能带走超过现今地月系统两倍以上的角动量,这一理论如果成立,可以极大改善大碰撞模型的角动量制约。
但出差共振理论并非由ćuk和Stewart(2012)首次提出,Touma和Wisdom(1994)就研究了在标准碰撞模型下出差共振运动对地月系统角动量的影响,认为出差共振运动将发生在月球轨道半长轴为4.6RE处(RE为地球半径)。ćuk和Stewart(2012)提出的高自旋地球碰撞模型碰撞后地月系统总角动量约为2LEM,更快速的旋转使得月球开始进入出差共振运动的位置增加到6.8RE,在这一距离上,月球被捕获进入出差共振运动的机率将大大增加。当月球一担被捕获并进入出差共振运动,月球轨道的长轴与太阳-地球轨道面将被固定而成90°夹角,地月的潮汐作用将地球的自转角动量输送给了月球,然而由于出差共振运动对月球轨道的锁定,因此这些角动量并没有转化成月球绕地球公转的角动量,这部分角动量被太阳所吸收,最终转化成地月系统绕太阳公转的角动量。ćuk和Stewart(2012)进一步说明,虽然在模拟过程中他们让地球轨道保持不变,但实际上,地球与太阳的间距会有微小的改变,地球绕太阳的轨道相应会有一个很小的增加。
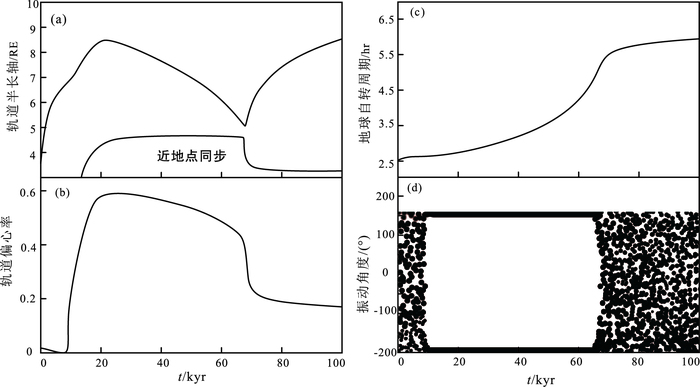
图 7为模拟的高自旋地球碰撞模型下地月系统的变化。设置初始地球自转周期为2.5 h,Q≈100(Q为潮汐作用能量耗散衡量参数),月球在与地球的间距为6.8RE的位置被捕获(月球形成以后的9000年左右时间),并一直持续到5RE的位置(月球形成以后的68000年左右)。在捕获之初,月球轨道半径将保持向外扩展(半长轴增加,图 7a),同时伴随了偏心率的增加(图 7b),此后偏心率降低,月球轨道半长轴将保持向内收缩直至5RE的距离。在月球被锁定这一过程中,地球的自转剧烈下降,自转周期从2.5 h下降到大约6 h(图 7c),这与现今的地球自转周期是相符的,在整个捕获过程中,共振角度在±180°左右变化(图 7d)。ćuk和Stewart(2012)还调整了初始的自转周期h以及参数Q,发现最终运行的结果与标准状况(图 7)基本一致。
|
引自ćuk and Stewart(2012) 图 7 高自旋地球碰撞模型下Evection resonance对地月系统的影响 Figure 7 The influence of evection resonance on the earth and the moon system in the fast-spinning earth impact model |
出差共振运动可以降低大碰撞模型的角动量制约,但学界对此尚未形成共识。Wisdom认为出差共振运动只有在很狭窄的参数范围内才能去除角动量,而且ć uk和Stewart的方法在Q值上存在缺陷。Wisdom和Tian(2015)采用了新的常数Q重新对ć uk和Stewart的模型进行了检验,得出了不同的结果,Wisdom的结果表明在出差共振运动中,角动量虽然可以被带走,但将被带走超额的角动量,剩余的角动量将比现今地月系统的角动量还要少。Wisdom还提出另外一种可能,即出差共振运动并非一种简单的振荡,而是一种循环的方式,在循环的方式下,角动量可能可以减少到比合理角动量略多的程度,但这种循环的方式还具有不确定性(Wisdom and Tian, 2015)。此外,Ward和Canup也认为出差共振运动在有些条件下可以带走大量角动量,有些条件下则不能(Ward and Canup, 2013)。
5 大碰撞模型的基础认识研究进展地月系统间的一系列观测事实和独特性质是大碰撞理论的基础,但由于天体研究的特殊性,这些观测事实和独特性质很多时候并不确定,近年来出现的一些新的认识,对大碰撞数值模型起到了重要的影响。
5.1 地月系统三氧同位素组成地月系统三氧同位素(Δ17O)组成一致是一个基本认识,这一认识已经成为大碰撞数值模型的一个关键制约因素。Herwartz等(2014)提出了与传统认识截然不同的观点,认为地球与月球之间的Δ17O并非完全一致。Herwartz系统收集了全球不同位置来源于大洋中脊玄武岩(MORB)以及地幔包裹体的10个样本,以及Appollo11、Appollo12、Appollo16共3个月球玄武岩样本,通过高精度的同位素分析技术,发现了地月系统Δ17O存在(12±3)×10-6的偏差。在假设碰撞体的组成为EL型和EH型顽火辉石球粒陨石,大小与火星类似的初始条件下,Herwartz测算了(12±3)×10-6的偏差对数值模型的影响,这一偏差可以将|δfT|的要求放宽到20%~50%的范围内,对应碰撞体物质在月球中占比为43%±13%,并认为这一结果能有效支持大碰撞理论。Herwartz等(2014)的结果在定性上非常重要,地月系统氧同位素存在差异的认识能够有效的放松数值模型的约束条件,对于建立新的大碰撞数值模型将具有非常重要的意义。
但Herwartz的结果在定量上实际上并不能彻底解决现有数值模型的同位素制约问题(定量结果与3个主要的数值模型并不一致,仅支持碰撞逃逸模型,对应|δfT|为35%~37%),同时也没有说明其他一些同位素在地月间的差异状况。
2016年最新工作对Herwartz等(2014)的结果再次提出了强烈挑战。Young等(2016)同样系统研究了地月系统样品的氧同位素,通过最新的高精度同位素分析技术更加全面的分析了14个月球样品和32个地球样品,Young的结果表明了地月系统间三氧同位素组成的偏差仅仅在(-1±5)×10-6之间,而后增薄层对地球Δ17O的影响在1×10-6左右,这一结果推翻了Herwartz等(2014)的认识。Young认为地月系统间Δ17O组成上的差异较小,同时5×10-6级别的差距则可能是大碰撞事件造成了碰撞体和原始地球物质混合的结果,因此他的结果可以支持近期的高能碰撞数值模型(高角动量模型)。事实上Young的结果让地月系统同位素组成重新回到基本一致的认识上,2012年的2个高角动量模型在提出时本身就是基于这一认识而建立的,因此这一结果稳定了2个高角动量模型的建立基础,但高角动量模型的最大问题在于需要出差共振运动来去除多余的角动量,而出差共振这一运动本身具有很大的不确定性(前文已论述)。另外,Bao等(2016)从三氧同位素分馏的机理出发,也认为Herwartz测量的偏差非常微小,即使在地球上,这样微小的差异也是存在的,因此不能作为地月系统间三氧同位素组成存在偏差的证据。
5.2 月球挥发分损失月球明显亏损挥发性元素(K、Pb、Bi等)也是一个重要的观测事实,挥发性元素的亏损一般被认为和大碰撞造成的热事件密切相关,因此月球贫挥发性元素一直被认为是大碰撞理论的重要支撑。
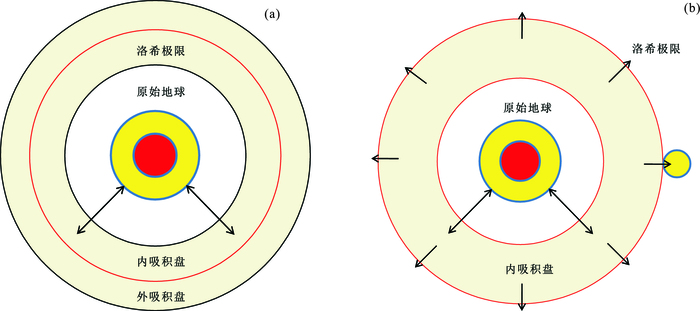
Salmon和Canup(2012)提出了一个两阶段吸积模型。这一模型中,吸积盘可以分为内吸积盘和外吸积盘(以洛希极限为界),第1阶段外吸积盘(超出洛希极限部分)的吸积时间较短,会首先吸积形成一个初始月球,第2阶段内吸积盘(未超出洛希极限部分)物质在热黏度调节作用及初始月球的引力共振作用下,会越过洛希极限,继续参与吸积,直至月球的形成。这一新的吸积模型会将月球的吸积时间延长至~ 100年左右(图 8)(Salmon and Canup, 2012,2014)。
|
图 8 两阶段吸积模型示意图 Figure 8 Sketches for the two stages accretion model |
Salmon和Canup一开始用这个模型解释地月系统同位素组分一致问题。Salmon & Canup认为外吸积盘会首先吸积形成一个初始月球,而内吸积盘(未超出洛希极限部分)在高温条件下将保持熔融和部分的气化状态,按照行星-吸积盘平衡理论,内吸积盘会与原始地球硅酸盐的气体部分会发生混合,使得内吸积盘与原始地球的地幔之间达到同位素组份的平衡。此后,在初始月球的引力共振和热梯度的作用下,内吸积盘的物质会继续参与月球吸积,直至月球的形成。这会形成内吸积盘物质包裹外吸积盘物质的状态,由于内吸积盘的物质已经与地球达到平衡,Salmon和Canup认为这一过程会使得月球外层物质呈现出与地球一致的同位素组成,掩盖月球深部的同位素组分信息,如图 9所示。这一理论将很容易被月球的深部样品所验证(但目前并无来自深部的直接样品),同时这一理论还需要考虑后期月球岩浆洋事件的广度和深度。总体而言,这一观点可以部分支持标准碰撞模型,但由于缺乏其他方面的证据,更接近于一种假设。
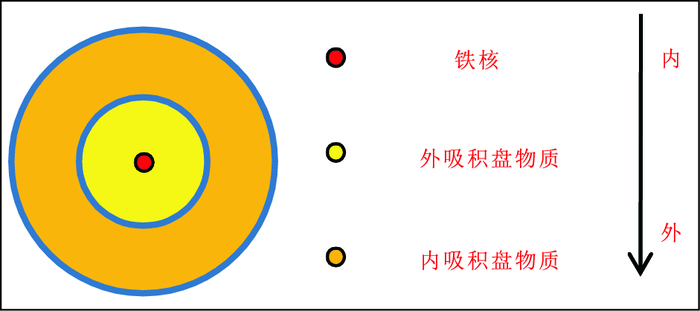
|
图 9 两阶段吸积模型形成的月球示意图 Figure 9 A sketch for the Moon formed by the two stages accretion model |
Canup等(2015)用这一模型来解释月球挥发分的损失,认为挥发分的缺失可能是由于月球形成过程中优先吸积了贫挥发分的熔融体,此后吸积作用中断造成。Canup采用MAGMA CODE对这一新的吸积模型进行了定量化,按照模拟结果,吸积盘同样由洛希极限分为内吸积盘和外吸积盘,外吸积盘会很快吸积(不到1年),此后吸积过程停滞了约20年的时间,内吸积盘的物质开始继续参与月球的吸积,由于内吸积盘最初是处于高温熔融状态,因此这部分熔融体是贫挥发分的,随着吸积盘的冷却,挥发分开始向熔体凝聚,但这一凝聚过程并没有完成,在引力的相互作用下,月球脱离了吸积盘,完成了吸积,这一过程持续时间约100年,因此月球最终缺失了中等以上的挥发性元素。这一过程中,外吸积盘提供的物质的量占月球总物质的量40%,内吸积盘提供了剩余60%的物质的量。这一吸积模型意义在于提供了月球挥发分缺失的另一种可能,并且延长了月球的吸积时间,将但它并不能排除高温状态下气相挥发性元素逃逸及后期火山作用的影响。如果这一模型成立,那么在月球深部有一定可能会有较高的挥发性元素含量(还需取决于外吸积盘吸积过程及全月的熔融程度)。
两阶段吸积模型对大碰撞理论的影响是正面的,一方面延长了吸积时间,部分支持了行星-吸积盘平衡理论(前文已论述),另一方面如果挥发分损失的方式成立,那么现在的月球形成理论中,也只有大碰撞产生的吸积盘可以提供支持这样一种吸积-中断机制,此外两阶段吸积模型还提供了地月组分一致的另一种可能。对具体的数值模型而言,两阶段吸积模型更支持高角动量模型。
5.3 碰撞体与原始地球的同位素组成碰撞体和原始地球的同位素组分不同(如:Δ 17O)一直以来也是一个基本认识。主要原因有:① 碰撞体来源于太阳系和地球轨道半径不同的位置,这是由于在地球轨道的Trojan点(Trojan点为星体轨道Lagrangian点中的2个稳定点,位于星体轨道前方和后方60°的位置)上,基本不可能形成一个火星大小的碰撞体;② 从太阳系行星形成的角度看,在距离太阳中心不同轨道上形成的星体,应该具有完全不同的同位素组成,从现在已知的太阳系内不同来源的陨石样品来看,它们的三氧同位素(Δ17O)组成完全不同,如火星SNC陨石,灶神星及小行星带陨石等。所以原始地球和碰撞体必然具有不同的同位素组成。
最近Battisti等(2015)等利用N-body方法在模拟太阳系行星形成过程中得到了新的认识,从统计学的角度表明了行星和碰撞体具有相同的同位素组成并非是一个小概率事件。Battisti采用了Mercury Code进行了40次模拟,每次模拟的范围为0.5Au~4.5Au,包含了85~80个星胚以及1000~2000个星子,17O的含量采用地球和火星的含量进行标准化,每次模拟通过星子与星胚间的碰撞产生了3~4个行星。Pahlevan和Stevenson也做过类似的模拟工作(Pahlevan et al., 2011;Pahlevan and Stevenson, 2007),他们的结论是碰撞体和行星的同位素组分一致的概率很低,但Battisti认为早期的工作分辨率不够,他们将计算分辨率提高了十倍,同时为了保证分辨率,Battisti在40次模拟中仅仅选取20次,选取的标准是最后阶段大碰撞的碰撞体和行星至少都由50个粒子构成。
高分辨率模拟结果表明碰撞体和行星的组分相似的碰撞比例可以达到20%~40%之间,更具普遍意义的是,最后阶段的大碰撞事件碰撞体与行星组分的相似性比其他阶段更高。Battisti的工作从统计上解释了地月系统间同位素组成一致的可能,支持了标准碰撞模型。但Battisti的工作仅仅计算了Δ17O,因此仍需进一步解释地月系统间其他同位素的组成一致问题(如28Si,29Si,30Si与182W/184W),此外Battisti采用的Δ17O偏差标准为(12±3)×10-6,如果按照新的Δ17O偏差标准(-1±5)×10-6,则Battisti的结论需要进行修正。同时由于这一结果是统计性结论,因此,还需要结合地月系统的一些特殊的观测事实,而且Battisti的二十次结果中,γ的最小值为0.206,与标准模型相差较大。
6 结论与展望目前的大碰撞数值模型都不能完全解释地月系统的独特性质,它们都需要额外的理论来弥补数值模型的缺陷,标准碰撞模型需要通过行星-吸积盘平衡理论来平衡地月系统间的元素组成,高自旋地球碰撞模型和对称地球碰撞模型可以让吸积盘与原始地球的组成类似,但它们需要出差共振运动来去除地月系统多余的角动量,碰撞逃逸模型则需要二者同时发生。而行星-吸积盘平衡理论与出差共振理论本身也并不完善,不足以弥补数值模型存在的缺陷。地月系统间的基本特性对大碰撞数值模型至关重要,但近年来的新结果和认识尚未对现行数值模型产生根本性影响。
大碰撞过程中,原始地球接受了大量的能量与角动量,然而我们现在却无法找到这一事件在地球上的任何痕迹(许英奎等,2012),这需要从更新的角度和更高的视野去思考这一问题,未来大碰撞数值模型可能的方向包括:① 发展新的大碰撞相关理论,如碰撞体由金属铁构成,碰撞后全部进入地核,或者碰撞体本身具有和地球类似的组成,或者碰撞体主要由冰构成(可能性很小)等;② 建立新的大碰撞数值模型,在碰撞参数的变化范围内,可能存在我们尚未发现的碰撞方式;③ 进一步深入研究行星-吸积盘平衡理论与出差共振理论,证明它们的正确性,并且在行星演化过程中是一种经常发生的事件;④ 在由原始地球和碰撞体碰撞组成的吸积盘中的过程中,可能存在一些我们忽视了的物理作用,影响了现行数值模型的结果。
在研究大碰撞数值模型时,还需要关注地月系统间的一些约束条件还具有不确定性(Sekine et al., 2011, 2014;Sekine and Genda, 2012)。① 月球的一些全月组份是不确定的;② 月球的年龄不确定,虽然月球形成晚于太阳系形成后至少30 Ma,但到底晚多久仍有争议;③ 一般认为月球经历过全月范围的岩浆洋,但一些月球的斜长石表明岩浆洋的范围可能是局部的;④ 虽然月球贫挥发分,但挥发分丢失的原因并不确定,可能是由于大碰撞事件,也可能是由于月球形成早期的火山作用,或者是由于月球的不完全吸积。这些不确定因素有可能会从根本上改变对月球起源问题的认识。
Appendix (参数说明):
γ~碰撞体与系统总质量比例,γ=Mi/(Mi+Mt);
vesc~地球逃逸速度,值为11.2 km/s;
vimp~碰撞速度;
vi~碰撞体速度;
mi~碰撞体质量;
mt~碰撞目标(行星)质量;
b~碰撞尺度参数(b=sin ξ,当ξ=90°时,b=1);
ξ~碰撞角度;
L~碰撞后行星-吸积盘系统总角动量;
LEM~地月系统现今角动量;
MD~碰撞后吸积盘质量;
M⊕~地球质量;
ML~月球质量;
δfT~碰撞后行星与吸积盘的组份差异,百分制;
RE~地球半径;
T~地球自转周期;
Q~潮汐作用能量耗散参数。
致谢: 本文的工作是在国家自然科学基金重大项目的支持,感谢项目组对本文研究工作的帮助,感谢课题组张明明博士提供的资料。
| [] | Agnor C B, Canup R M, Levison H F. 1999. On the character and consequences of large impacts in the late stage of terrestrial planet formation. Icarus, 142(1): 219–237. DOI:10.1006/icar.1999.6201 |
| [] | Asphaug E. 2014. Impact origin of the moon?Annual Review of Earth and Planetary Sciences, 42:551-578 |
| [] | Bao H M, Cao X B, Hayles J A. 2016. Triple Oxygen Isotopes:Fundamental Relationships and Applications. Annual Review of Earth and Planetary Sciences, 44: 463–492. DOI:10.1146/annurev-earth-060115-012340 |
| [] | Barr A C, Canup R M. 2008. Constraints on gas giant satellite formation from the interior states of partially differentiated satellites. Icarus, 198(1): 163–177. DOI:10.1016/j.icarus.2008.07.004 |
| [] | Barr A C, Citron R I, Canup R M. 2010. Origin of a partially differentiated Titan. Icarus, 209(2): 858–862. DOI:10.1016/j.icarus.2010.05.028 |
| [] | Barr A C, Canup R M. 2010. Origin of the Ganymede-Callisto dichotomy by impacts during the late heavy bombardment. Nature Geoscience, 3(3): 164–167. DOI:10.1038/ngeo746 |
| [] | Benz W, Slattery WL, Cameron A G W. 1986. Short note:Snapshots from a three-dimensionalmodeling of a giant impact. In:Hartmann WK, Phillips RJ, Taylor GJ, eds. Origin of the Moon. Houston, TX:Lunar and Planetary Institute, 617-620 |
| [] | Cameron AGW, Ward WR. 1976. The origin of the Moon. Lunar and Planetary Science Conference, 7: 120. |
| [] | Canup R M, EspositoL W. 1996. Accretion of the moon from an impact-generated disk. Icarus, 119(2): 427–446. DOI:10.1006/icar.1996.0028 |
| [] | Canup R M, Asphaug E. 2001. Origin of the Moon in a giant impact near the end of the Earth's formation. Nature, 412(6848): 708–712. DOI:10.1038/35089010 |
| [] | Canup R M, Ward W R, Cameron A G W. 2001. A scaling relationship for satellite-forming impacts. Icarus, 150(2): 288–296. DOI:10.1006/icar.2000.6581 |
| [] | Canup R M. 2004. Simulations of a late lunar-forming impact. Icarus, 168(2): 433–456. DOI:10.1016/j.icarus.2003.09.028 |
| [] | CanupR M. 2005. A giant impact origin of Pluto-Charon. Science, 307(5709): 546–550. DOI:10.1126/science.1106818 |
| [] | Canup R M, Ward W R. 2006. A common mass scaling for satellite systems of gaseous planets. Nature, 441(7095): 834–839. |
| [] | Canup R M. 2008. Lunar-forming collisions with pre-impact rotation. Icarus, 196(2): 518–538. DOI:10.1016/j.icarus.2008.03.011 |
| [] | Canup R M. 2010. Origin of Saturn's rings and inner moons by mass removal from a lost Titan-sized satellite. Nature, 468(7326): 943–946. DOI:10.1038/nature09661 |
| [] | Canup R M. 2012. Forming a Moon with an Earth-like Composition via a Giant Impact. Science, 338(6110): 1052–1055. DOI:10.1126/science.1226073 |
| [] | Canup R M, Barr A C, Crawford D A. 2013. Lunar-forming impacts:High-resolution SPH and AMR-CTH simulations. Icarus, 222(1): 200–219. DOI:10.1016/j.icarus.2012.10.011 |
| [] | Canup R M. 2014. Lunar-forming impacts:Processes and alternatives. Philosophical Transactions of the Royal Society A-Mathematical, Physical, and Engineering Sciences, 372(2024): 20130175. DOI:10.1098/rsta.2013.0175 |
| [] | Canup R M, Visscher C, Salmon J, FegleyBJr. 2015. Lunar volatile depletion due to incomplete accretion within an impact-generated disk. Nature Geoscience, 8(12): 918–921. DOI:10.1038/ngeo2574 |
| [] | Canup R M. 2015. Solar system:An incredible likeness of being. Nature, 520(7546): 169–170. |
| [] | Citron R I, Genda H, Ida S. 2015. Formation of Phobos and Deimos via a giant impact. Icarus, 252: 334–338. DOI:10.1016/j.icarus.2015.02.011 |
| [] | Crawford D A, Taylor P A, Bell R L. 2006. Adaptive mesh refinement in the CTH shock physics hydrocode. Химическаяфизика, 25(9): 72–77. |
| [] | Crawford D A, Kipp M E. 2010. Giant impact theory for origin of the Moon:High resolution CTH simulations. Lunar and Planetary Science Conference, 5: 1405. |
| [] | ćuk M, StewartS T. 2012. Making the moon from a fast-spinning earth:A giant impact followed by resonant despinning. Science, 338(6110): 1047–1052. DOI:10.1126/science.1225542 |
| [] | Daly RA. 1946. Origin of the Moon and its topography. Proceedings of the American Philosophical Society, 90(2): 104–119. |
| [] | Genda H, Kokubo E, Ida S. 2007. Imperfect accretion during the giant impact stage of terrestrial planet formation. GeochimicaetCosmochimicaActa, 71(15). |
| [] | Genda H, IkomaM. 2008. Origin of the ocean on the Earth:Early evolution of water D/H in a hydrogen-rich atmosphere. Icarus, 194(1): 42–52. DOI:10.1016/j.icarus.2007.09.007 |
| [] | Genda H, Fujita T, Kobayashi H, Tanaka H, Abe Y. 2015. Resolution dependence of disruptive collisions between planetesimals in the gravity regime. Icarus, 262: 58–66. DOI:10.1016/j.icarus.2015.08.029 |
| [] | Genda H, Abe Y. 2002. Effects of giant impacts on the atmosphere formation. GeochimicaetCosmochimicaActa, 66(15A): A270. |
| [] | GendaH, Abe Y. 2003. Survival of a proto-atmosphere through the stage of giant impacts:The mechanical aspects. Icarus, 164(1): 149–162. DOI:10.1016/S0019-1035(03)00101-5 |
| [] | GendaH, Abe Y. 2005. Enhanced atmospheric loss on protoplanets at the giant impact phase in the presence of oceans. Nature, 433(7028): 842–844. DOI:10.1038/nature03360 |
| [] | Georg R B, Halliday A N, Schauble E A, Reynolds B C. 2007. Silicon in the Earth's core. Nature, 447(7148): 1102–1106. DOI:10.1038/nature05927 |
| [] | Halliday A N, Lee D C, Porcelli D, Wiechert U, Sch nbächler M, Rehkämper M. 2001. The rates of accretion, core formation and volatile loss in the early Solar System. Philosophical Transactions:Mathematical, Physical and Engineering Sciences, 359(1787): 2111–2135. DOI:10.1098/rsta.2001.0901 |
| [] | Hamano K, Abe Y, Genda H. 2013. Emergence of two types of terrestrial planet on solidification of magma ocean. Nature, 497(7451): 607–610. DOI:10.1038/nature12163 |
| [] | Hartmann WK, Davis DR. 1975. Satellite-sized planetesimals and lunar origin. Icarus, 24(4): 504–515. DOI:10.1016/0019-1035(75)90070-6 |
| [] | Herwartz D, Pack A, Friedrichs B, Bischoff A. 2014. Identification of the giant impactor Theia in lunar rocks. Science, 344(6188): 1146–1150. DOI:10.1126/science.1251117 |
| [] | Humayun M, Clayton R N. 1995a. Potassium isotope cosmochemistry:Genetic implications of volatile element depletion. GeochimicaEtCosmochimicaActa, 59(10): 2131–2148. |
| [] | Humayun M, Clayton R N. 1995b. Precise determination of the isotopic composition of potassium:Application to terrestrial rocks and lunar soils. GeochimicaEtCosmochimicaActa, 59(10): 2115–2130. |
| [] | Ida S, Canup R M, Stewart G R. 1997. Lunar accretion from an impact-generated disk. Nature, 389(6649): 353–357. DOI:10.1038/38669 |
| [] | Kipp ME, Melosh HJ. 1986. A preliminary numerical study of colliding planets. Lunar and Planetary Institute, 643-647 |
| [] | Lock S J, Stewart S T, Petaev M I, Leinhardt Z M, Mace M, Jacobsen S B, Cuk M. 2016, A New Model for Lunar Origin:Equilibration with Earth Beyond the Hot Spin Stability Limit. Lunar and Planetary Science Conference. 47:2881. |
| [] | Lugmair G W, Shukolyukov A. 1998. Early solar system timescales according to53Mn-53Cr systematics. GeochimicaEtCosmochimicaActa, 62(16): 2863–2886. |
| [] | Mastrobuono-Battisti A, Perets H B, Raymond S N. 2015. A primordial origin for the compositional similarity between the Earth and the Moon. Nature, 520(7546): 212–215. DOI:10.1038/nature14333 |
| [] | Melosh H J, Stevenson D J, Canup R. 2013. Credit for impact theory. Science, 342(6165): 1445–1446. |
| [] | Nakajima M, Ikoma M, Genda H. 2007. Effects of hydrogen on limits of radiative emission from a planet with a saturated-water-vapor atmosphere. Geochimicaet CosmochimicaActa, 71(15): A702–A702. |
| [] | Pahlevan K, StevensonD J. 2007. Equilibration in the aftermath of the lunar-forming giant impact. Earth and Planetary Science Letters, 262(3-4): 438–449. |
| [] | Pahlevan K, Stevenson D J, Eiler J M. 2011. Chemical fractionation in the silicate vapor atmosphere of the Earth. Earth and Planetary Science Letters, 301(3-4): 433–443. DOI:10.1016/j.epsl.2010.10.036 |
| [] | Raymond S N, O'Brien D P, Morbidelli A, Kaib N A. 2009. Building the terrestrial planets:Constrained accretion in the inner Solar System. Icarus, 203(2): 644–662. DOI:10.1016/j.icarus.2009.05.016 |
| [] | Reufer A, Meier MMM, Benz W, Wieler R. 2012. A hit-and-run giant impact scenario. Icarus, 221(1): 296–299. DOI:10.1016/j.icarus.2012.07.021 |
| [] | Salmon J, Canup R M. 2012. Lunar accretion from a Roche-interior fluid disk. The Astrophysical Journal, 760(1): 83. DOI:10.1088/0004-637X/760/1/83 |
| [] | Salmon J, Canup R M. 2014. Accretion of the Moon from non-canonical discs. Philosophical Transactions of the Royal Society of London A:Mathematical, Physical, and Engineering Sciences, 372(2024): 20130256. DOI:10.1098/rsta.2013.0256 |
| [] | Sekine Y, Genda H, Sugita S, Kadono T, Matsui T. 2011. Replacement and late formation of atmospheric N2 on undifferentiated Titan by impacts. Nature Geoscience, 4(6): 359–362. DOI:10.1038/ngeo1147 |
| [] | Sekine Y, Genda H. 2012. Giant impacts in the Saturnian system:A possible origin of diversity in the inner mid-sized satellites. Planetary and Space Science, 63-64: 133–138. |
| [] | Sekine Y, Genda H, Muto Y, Sugita S, Kadono T, Matsui T. 2014. Impact chemistry of methanol:Implications for volatile evolution on icy satellites and dwarf planets, and cometary delivery to the Moon. Icarus, 243: 39–47. DOI:10.1016/j.icarus.2014.08.034 |
| [] | Shearer C K, Hess P C, Wieczorek M A, Pritchard M E, Parmentier E M, Borg L E, Longhi J, Elkins-Tanton L T, Neal C R, Antonenko I, Canup R M, Halliday A N, Grove T L, Hager B H, Lee D C, Wiechert U. 2006. Thermal and magmatic evolution of the Moon. Reviews in Mineralogy and Geochemistry, 60(1): 365–518. DOI:10.2138/rmg.2006.60.4 |
| [] | Shukolyukov A, Lugmair G W, Macisaac C. 1998. Chromium in the Cretaceous-Tertiary boundary layer:First isotopic evidence for an impactor and its type. Meteoritics and Planetary Science, 33: A144–A145. |
| [] | ShukolyukovA, Lugmair G W. 1998. Isotopic evidence for the Cretaceous-Tertiary impactor and its type. Science, 282(5390): 927–930. DOI:10.1126/science.282.5390.927 |
| [] | Touboul M, Kleine T, Bourdon B, Palme H, Wieler R. 2007. Late formation and prolonged differentiation of the Moon inferred from W isotopes in lunar metals. Nature, 450(7173): 1206–1209. DOI:10.1038/nature06428 |
| [] | Touma J, Wisdom J. 1994. Evolution of the Earth-Moon system. The Astronomical Journal, 108(5): 1943–1961. |
| [] | Wada K, Kokubo E, Makino J. 2006. High-resolution simulations of a Moon-forming impact and post-impactevolution. The Astrophysical Journal, 638: 1180–1186. DOI:10.1086/apj.2006.638.issue-2 |
| [] | Ward W R, Canup R M. 2000. Origin of the Moon's orbital inclination from resonant disk interactions. Nature, 403(6771): 741–743. DOI:10.1038/35001516 |
| [] | Ward W R, Canup R M. 2010. Circumplanetarydisk formation. Astronomical Journal, 140(5): 1168–1193. DOI:10.1088/0004-6256/140/5/1168 |
| [] | Ward W R, Canup R M. 2013. The evection resonance and the angular momentum of the Earth-Moon system. In:44thLunar and Planetary Science Conference. The Woodlands, Texas, 1719: 3029. |
| [] | Wiechert U, Halliday A N, Lee D C, Snyder G A, Taylor L A, Rumble D. 2001. Oxygen isotopes and the Moon-forming giant impact. Science, 294(5541): 345–348. DOI:10.1126/science.1063037 |
| [] | Wisdom J, Tian Z L. 2015. Early evolution of the Earth-Moon system with a fast-spinning Earth. Icarus, 256: 138–146. DOI:10.1016/j.icarus.2015.02.025 |
| [] | Yonezawa T, Genda H, Koumoto K. 2003. Cationic Silver Nanoparticles Dispersed in Water Prepared from Insoluble Salts. Chemistry Letters, 32(2): 194–195. DOI:10.1246/cl.2003.194 |
| [] | Young E D, Kohl I E, Warren P H, Rubie D C, Jacobson S A, Morbidelli A. 2016. Oxygen isotopic evidence for vigorous mixing during the Moon-forming giant impact. Science, 351(6272): 493–496. DOI:10.1126/science.aad0525 |
| [] | Zhang JJ, Dauphas N, Davis A M, Leya I, Fedkin A. 2012. The proto-Earth as a significant source of lunar material. Nature Geoscience, 5(4): 251–255. DOI:10.1038/ngeo1429 |
| [] | 林杨挺. 2010. 月球形成和演化的关键科学问题. 地球化学, 39(1): 1–10. |
| [] | 欧阳自远, 刘建忠. 2014. 月球形成演化与月球地质图编研. 地学前缘, 21(6): 1–6. |
| [] | 许英奎, 朱丹, 王世杰, 刘耘. 2012. 月球起源研究进展. 矿物岩石地球化学通报, 31(5): 516–521. |
 2017, Vol. 36
2017, Vol. 36

