锆石U-Pb定年是大型离子探针(SIMS,包括SHRIMP系列和CAMECA系列仪器)的主要应用之一,特点是空间分辨率高,以10 nA的一次O2-束流,在一个常规束斑20×30 μm椭圆面积上剥蚀12 min,剥蚀深度小于1 μm,总消耗锆石量在2 ng左右。如此低的样品量而要获得高精度的数据,从统计学角度分析,二次离子计数越多,分析误差则会越小。按这个思路,相同仪器条件下分析年龄相近的样品,锆石U(Pb)含量越高,理论上获得的数据精确度更高。然而,研究中越来越多的实例显示,理论上年龄一致的锆石,如简单岩浆岩中的锆石,在较低U含量范围(<1000×10-6)的锆石U-Pb表观年龄相对一致,而在U含量高到一定程度之后,U-Pb表观年龄经常随U含量(一般大于2000×10-6)有明显的偏高现象,被称为“高U效应”(Williams and Hergt,2000; Li et al.,2010,2013; White and Ireland,2012; Gao et al.,2014)。那么“高U效应”对锆石定年的影响如何?是如何造成的?是否可以通过一定的措施消除?本文通过总结部分该方面的研究报道,并结合从事离子探针锆石U-Pb定年的多年经验,谈谈自己的认识,以期进行广泛的交流和讨论。
1 高U锆石的定年表现笔者曾就发表的近5万个锆石U含量数据进行过统计,锆石U含量范围为从0.01×10-6以下到高达10%,但90%以上样品U含量范围为100×10-6~1000×10-6之间。由以上数据可见,高U含量的锆石并不常见,但涉及到某些特定的岩石样品时就较为常见,如青藏高原的淡色花岗岩、华南的含W-Zn矿花岗岩,这些经历过高分异作用的岩浆结晶出的锆石大大多U含量非常高,在离子探针测试中难以得到理想的结果。
1.1 精确测量的难点238U半衰期为44.68亿年,略低于地球年龄,目前地球样品中的锆石 206 Pb 含量至多只有U含量的一半,25亿年以来的样品只有U含量的1/4或更低,因而U-Pb定年重点在Pb的精确测量,而U的测量相对容易,然而过高的U含量却带来困难。锆石离子探针定年的Pb+/U+分馏校正需要相应的UO+/U+(SHRIMP仪器,Ireland and Williams,2003)或UO+2/U+(CAMECA 仪器,Li et al.,2009,2010),一般采用单个离子计数器作为接收杯,通过跳峰的方式依次接收Pb同位素和U相关离子(U、UO或UO2)。离子计数器被设计为接收低信号峰,一般在50万cps(counts per second)内可有较好的精度,过高强度的离子轰击会造成计数器的加速老化。Pb的离子化产率一般在20 cps/10-6/nA左右,UO+2与Pb+大体相当,UO+有近高一倍的离子化产率,而U+约只有1/4的产率。可以计算出,如果一次离子束(一般采用O-2)强度在10 nA,测量最高产率的UO+,50万cps只能容忍1250×10-6的U,而UO+2则可以宽限到2500×10-6 U。SHRIMP仪器的U-Pb定年Pb/U分馏校正采用Pb+/U+vs. UO+/U+的幂函数关系,为适应更宽的U含量范围,锆石定年时一次离子束强度设在4 nA或更低,这样锆石U含量在3000×10-6之内可以在50万 cps;而CAMECA离子探针锆石定年Pb/U分馏校正采用Pb/U vs. UO+2/U+的幂函数关系,这样可以用更高的一次离子强度,以获得更高的Pb+离子信号并达到更高的统计精度。但是,如果锆石U含量超过3000×10-6,会造成UO+或UO+2信号强度远超50万cps,造成离子计数器的快速老化,老化的离子计数器将会损失计数率,从而使得UO+或UO+2信号强度失真。从保护仪器这一角度来说,不适宜分析高U锆石。大幅降低一次离子强度似乎可行,但这又会造成低U锆石分析误差偏大,得不偿失。
1.2 年龄数据的表现理论上讲,高U锆石放射性损伤强度高,易于导致锆石晶格的破坏,因而放射成因Pb容易丢失,这样所获得的U-Pb表观年龄会由于U含量升高而变低。这种情况更多的见于将锆石溶解再提取U-Pb进行热质谱测试的ID-TIMS方法分析结果,放射性损伤高的锆石发生Pb丢失后会出现不谐和U-Pb体系。在离子探针锆石分析的实例中,较老的锆石会出现这种理论上的情况(图 1a),而偏年轻的高U锆石更多地具有随U含量升高而偏高的U-Pb表观年龄(图 1b),一般在2000×10-6 U含量以上有所体现,随U含量升高U-Pb表现年龄偏差可达30%以上。对华南西华山花岗岩的锆石的大量测试统计发现,当U含量高到30000×10-6以上时,部分锆石U-Pb表观年龄有明显的偏低趋势,即放射成因Pb丢失的现象清晰显现(图 1c),这在西藏年轻的淡色花岗岩锆石研究中也有类似现象(图 1d,刘志超博士论文)。总结目前的表观现象来看,高U锆石不仅会受到“高U效应”使得U-Pb表观年龄升高的影响,同时可能会受到放射成因Pb丢失效应影响而表观年龄变低。可见,就单个高U锆石测点来说,其年龄可高可低,自然也会有一部分落在与同一样品低U锆石年龄一致的范围内,因此不能仅以几个锆石高U但年龄并不偏高的现象来指示锆石U含量高对离子探针分析无影响,其实是受到了双重效应影响所致。对于高U锆石离子探针测试的结果就单点来说U-Pb年龄难以测准,但多点测试后以Pb/U年龄对U含量作图,可以大体归纳出较为合理的年龄,如 图 1c、1d所示。

|
(a)年龄较老的锆石,U含量越高放射成因Pb丢失越多;(b)一般“高U效应”表现为随U含量升高而Pb/U表观年龄偏老;(c),(d)高U锆石可同时存在偏老的“高U效应”和偏年轻的Pb丢失效应 图 1 高U锆石离子探针U-Pb定年的实际表现 Fig. 1 The actual performance of SIMS U-Pb dating results of the high-U zircon |
“高U效应”的表现是离子探针分析所获得的锆石 206 Pb/238U表观年龄偏高,这就需要从离子探针锆石U-Pb定年的计算原理上来看,具体的离子探针锆石U-Pb定年原理可参见相关文献,如Ireland和Williams(2003),杨亚楠等(2014),这里只简单描述。离子探针矿物定年Pb/U采用标准比对法,在相同仪器条件下分析标准样品获得实测值与推荐值的比例关系,然后应用到未知样品的测量值中计算其真实值。对锆石U-Pb定年的Pb/U值测定有如下关系:
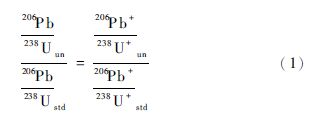
式中:下脚注un代表未知样品,std代表标准样品,Pb均为放射性成因Pb。
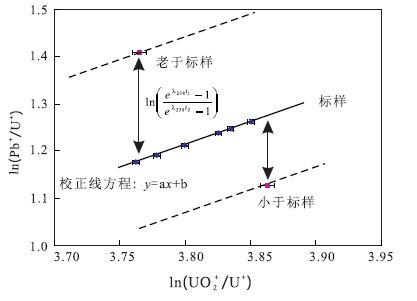
因为每个测点位置晶轴方向差异、U含量高低不同、晶格完整性不同、仪器条件略有不同等诸多因素,均一标样也会有不同的Pb+/U+值,统计发现,Pb+/U+与UO+/U+或UO+2/U+呈很好的相关性,目前较为普遍的做法是描述为幂函数相关关系,因而表示在对数坐标图上,ln(Pb+/U+)与ln(UO+x/U+)呈直线关系,如 图 2表示。每次测量过程中,同一标样拟合为一直线,未知样测点落在标样线上方的点则表示老于标样,反之则较标样年龄年轻,到标样线的Y方向距离就是未知样与标样的年龄差。
|
年龄均一的标样在连续测试时间段内ln(Pb+/U+)vs. ln(UO+2/U+)可拟合为一直线,未知样落在线上,表明Pb/U表观年龄老于标样,反之落在线下,则年龄小于标样 图 2 离子探针锆石U-Pb定年Pb/U分馏校正的一般原理 Fig. 2 The general principle for calibrating Pb/U fractionation during SIMS zircon U-Pb analysis |
“高U效应”导致通过标准锆石校正Pb/U分馏后,所计算的U-Pb表观年龄偏老了,从校正原理图上可以看出,存在2个可能: ①Pb+/U+值升高了;②UO+x/U+降低了。也即是高U锆石具有不同于标准锆石样品的Pb/U分馏行为,因此需要考查高U锆石相较标准锆石的特殊性。
2.1 锆石的放射性损伤α衰变、 β衰变是主要的衰变类型,其中α衰变即为放射出一个α粒子,即质量数为4的He核,β衰变是释放出β粒子,即一个电子或正电子。α衰变涉及的母子核质量差大,根据质能方程可知衰变能也大,足以引起矿物晶格发生位错。238U、235U和232Th衰变经过一系列的中间子体,最终分别成为稳定的 206 Pb、 207 Pb、 208 Pb,这几个衰变过程分别释放了8、7、6个α粒子,在相同的时间内U含量越高,产生越多的α衰变,因此高U锆石的放射性损伤相对低U锆石也会更高。可以通过以下公式计算锆石形成以来经历了多大程度的α粒子轰击:
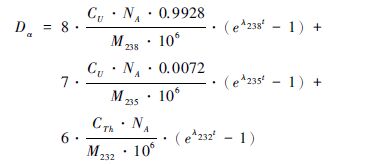
式中:CU和CTh是现在锆石中的U和Th含量(×10-6),NA是阿弗加德罗常数(6.022×1023),M238、M235和M232分别为U和Th母核的原子量,λ为相应母核的衰变常数,t为锆石结晶时间。这个公式是基于现在的U-Th含量和U-Th-Pb衰变方程,只是将重量转换为原子个数,Dα单位一般为1018 α/g(也有1016 α/mg)。 材料科学研究中因为涉及到多种矿物成分,为便于对比,多采用Ddpa(displacements per atom)为单位,标定每个原子受到粒子辐射后的影响程度,当研究某一特定矿物时,Dα和Ddpa存在固定比率关系。对于锆石而言,Ddpa~Dα×4.8×10-20。
衰变过程都遵从电荷数守恒、质量数守恒和能量守恒,α衰变能Qα以α粒子的动能Eα和子核的反冲能Ey的形式体现:Qα=Eα+Ey。对U(Th)质量数~230的原子核,α粒子的动能约占衰变能的98%,子核的反冲能约占衰变能的2%。根据α粒子的动能测量,发现大部分核素放出α粒子可分为4~8.8 MeV之间不同确定值的几群。不同的α粒子能量的放射性核素具有不同的半衰期,半衰期长短同α粒子能量有强烈的依赖关系。例如238U放射的α粒子能量是4.20 MeV,而212Po放射的α粒子能量是8.78 MeV,相差2.1倍,而238U的半衰期是4.468×109年,而212Po的半衰期是3.0×10-7 s,却相差1023倍。这反映了α粒子能量的微小改变引起了半衰期的巨大变化,所发射的α粒子能量越小,半衰期越长,反之能量越大,半衰期越短。
α粒子穿透能力很差,一般在距离母核10~30 μm范围即可停留下来,形成一个间隙粒子,造成一个点缺陷。相对于α粒子的动能,剩余子核反冲能约为 100 K电子伏量级,但造成可持续的级联膨胀,在~30 nm范围级别大量原子位移,形成纳米尺度的非晶形团簇。通过计算机模拟可以理论计算出U衰变过程中所释放每个α粒子造成晶胞原子位移的情况,具体可参见Nasdala等(2001)附录计算内容,这里只简单总结一下最主要的U-Pb衰变链计算结果,衰变链中每个α粒子的能量不同,所能造成位移原子个数也不同,α粒子直接造成的晶格空位从118到134个不等,平均在125个左右,而子核反冲所造成的晶格空位从590到1100不等,平均在788个左右。可见,放射性晶格损伤主要是子核反冲所导致的,但近来研究发现,α粒子辐射造成的损伤也不容忽视,锆石高U部位所释放的α粒子会造成相邻~20 μm范围内低U部位的强损伤(Nasdala et al.,2005)。
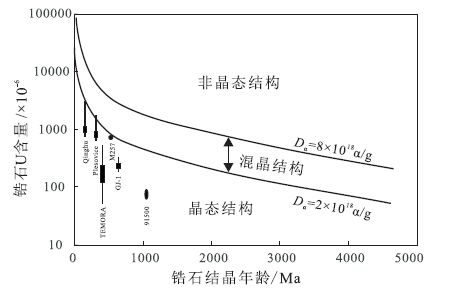
对锆石放射性损伤的研究可以分为几类:①对天然样品进行分析,根据U含量和年龄计算(如Chakoumakos et al.,1987; Murakami et al.,1991; Nasdala et al.,1995,2001,2005,2010);②人工合成锆石,添加短半衰期的Pu来代替U,研究一段时间后的锆石晶格参数变化(如Weber et al.,1994);③通过一定能量的粒子(如Kr+)轰击锆石来研究晶格损伤(如Meldrum et al.,1998)。发生放射性损伤的锆石会有一系列的性质改变,如晶胞参数、密度、体积、光学性质、硬度、弹性系数、热导率、溶解率等(参见Ewing et al.,2003)。例如,锆石的密度随损伤程度增加而降低,从4.7 g/cm3到3.9 g/cm3之间变化,在初始低辐射(<2×1018 α/g)阶段变化不大,在2×1018~8×1018 α/g阶段快速降低,而在将近完全蜕晶化阶段逐渐趋近于3.9 g/cm3(Murakami et al.,1991)。密度变低反映了晶格损伤后非晶质态部分体积的增大(Weber et al.,1994)。晶质锆石是单轴晶,有两个折光率,N0=1.924,Ne=1.984,在Dα<2×1018 α/g时,折光率基本没有变化,之后会随辐射强度增加而降低,完全蜕晶化的锆石成为均质体,折射率会降低到N0=Ne=1.81。总起来看,在未经过后期热愈合影响的前提下,当Dα<2×1018 α/g时,锆石总体处于晶格完整状态,2×1018 α/g<Dα<8×1018 α/g时处于过渡阶段,锆石物理性质转变快,当Dα>8×1018 α/g时,锆石总体处于完全蜕晶化状态(图 3)。自然条件下的锆石会或多或少地经历后期的热愈合,因此所观测到的锆石晶格损伤程度相对理论计算的Dα所能影响的程度要低。
|
Qinghu(Li et al., 2009),Plešovice(Slama et al., 2008),M257(Nasdala et al., 2008),TEMORA(Black et al., 2004),GJ-1(Jackson et al., 2004),91500(Wiedenbeck et al., 1995)等常用锆石标样均投点在损伤程度低、保持晶态结构区域 图 3 锆石U-Th的α辐射及核反冲效应可造成的锆石结晶状态改变程度 Fig. 3 The changing degree of zircon crystal state caused by the α radiation and nuclear recoil effects of the U-Th decay |
相同年龄的一组锆石,U含量越高放射性损伤越高,导致晶格的破坏越强。因此,很自然地推测晶格发生破坏部位Pb+离子化效率较晶格尚好的标准锆石要高(Black et al.,1991; McLaren et al.,1994; White and Ireland,2012; Gao et al.,2014),如此偏高的Pb+/U+导致了偏高的年龄。然而目前为止,尚没有确切证据支持这一假设。研究发现,在相同仪器条件下,NIST 610玻璃的Pb+离子产率大约只有锆石Pb+离子产率的50%,不同于锆石的实际观测Pb+/U+较真实Pb/U高2~4倍的情况,玻璃的Pb+/U+较真实值略微偏小(Stern and Amelin,2003)。如果锆石蜕晶化后成为无序的玻璃态,那么Pb+产率不但不会升高,而更可能会降低。通过对比,高U锆石的Pb+产率并没有明显的升高或降低,说明锆石的蜕晶化状态和玻璃态是不同的。Pb+/U+偏高更多原因还需从U+角度来考虑。
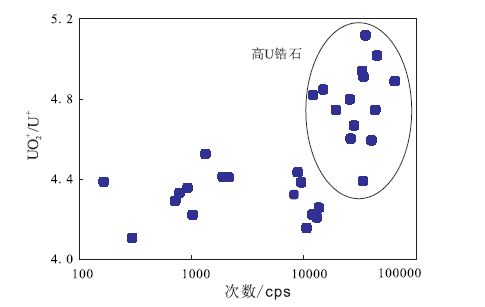
有研究者推测电子倍增器在高计数率下线性变差,U+的信号读数较真实值偏小了,因而Pb+/U+变高了(Leech,2008)。锆石U+产率很低,一次离子束在4 nA时(SHRIMP工作条件),10000×10-6 U含量,U+信号强度约有200 000 cps,对于离子探针消耗性电子倍增器(采用高电压维持95%以上高效率,半年到一年需要更换)的参数条件来说,这样的计数率一般不会造成明显的线性变差,除非是电子倍增器长时间未进行高压调节或已经坏掉了。但是锆石的UO+2和UO+信号较U+信号要高3~6倍,如果电子倍增器线性变差,那么UO+和UO+2受到的影响就更强,这样UO+n/U+会变低。根据 图 2所示,Pb+/U+升高和UO+n/U+降低都会导致计算所得年龄偏老。White和Ireland(2012)用SHRIMP系列仪器对高U锆石的研究也显示出高U锆石的UO+/U+相对标准锆石的UO+/U+偏低现象,这样看来,这个理由似乎很合理。然而进一步推论,如果是由于EM效率变差导致,则越强的信号计数损失越多,越高的U含量则UO+n/U+则会越低,这和实际情况不符合。对比高U锆石和锆石标样的数据发现,CAMECA 仪器样品表面吹氧条件下实际测量的UO+2/U+随U含量升高而变高(图 4),White和Ireland(2012)用SHRIMP系列仪器也显示出UO+/U+随U含量升高而升高的类似趋势。因此,这种UO+n/U+随U含量升高的现象说明电子倍增器线性变差不能解释“高U效应”。
|
图 4 离子探针锆石测试U+计数与相应UO+2/U+值关系 Fig. 4 he relationship between U+counts and corresponding UO+2/U+ratios during SIMS zircon analysis |
解释“高U效应”还需要从高U锆石的微观状态来分析。研究发现,完全无序化锆石在热愈合过程中,随温度升高逐渐成为一种混晶状态。首先在无定形的SiO2中出现大量纳米级四方晶系ZrO2,之后随温度升高,出现纳米级ZrSiO4微晶体(如McLaren et al.,1994;Nasdala et al.,2002)。在这样的混合体中,U会优先进入ZrO2和ZrSiO4微晶体,而Pb更易于进入无定形的SiO2中。离子探针对古老经历超高温变质的锆石分析发现了放射成因Pb分布的不均一性(Williams et al.,1984; Kusiak et al.,2013; Whitehouse et al.,2014),用原子探针分析也证实了锆石中Pb分布的不均一性,但仅在几到几十纳米尺度(Valley et al.,2014)。在对斜锆石(一般是单斜晶系ZrO2)的离子探针U-Pb定年研究中发现,斜锆石的U+离子产率较锆石要低,样品表面吹氧后,斜锆石的UO+n/U+相对锆石的UO+n/U+高一倍以上,而样品表面不吹氧时,UO+n/U+相对锆石的UO+n/U+要低(Li et al.,2010)。自然界中经历损伤的高U锆石处于这种混晶状态时,U含量越高则纳米级ZrO2越多,这样离子探针测试时U+产率相对越低,而处于无定性SiO2中的Pb离子产率受影响不大,因而出现Pb+/U+升高的状态,导致表观年龄偏老。UO+n/U+的变化趋势非常支持这一推论,图 2所示CAMECA仪器表面吹氧条件下观测到高U锆石UO+2/U+相对标准锆石偏高,且与U含量有正相关性。SHRIMP系列仪器锆石分析样品表面不吹氧,观测到高U锆石UO+/U+相较标准锆石偏低,但存在与锆石U含量的正相关关系(White and Ireland,2012的图10)。研究中也会发现一些锆石颗粒U含量并不很高,但同样存在类似的“高U效应”现象,这可能是古老的蜕晶化锆石不完全重结晶的结果,晶格内仍存在可观的ZrO2。总之,无论是锆石损伤后分解出ZrO2或蜕晶化后再愈合过程中新生长出ZrO2,都会在纳米尺度发生U-Pb的分离,由于不同基体Pb+和U+的离子化效率差异导致了所谓的“高U效应”。
3 应对措施综上所述,可见“高U效应”和锆石的放射性损伤有关,要避免其影响,需要测试前尽可能避免损伤锆石,或者试着愈合其损伤,如果都是高U锆石,则最好用其他矿物来代替了。
3.1 避免损伤锆石在早期质谱仪器灵敏度不高的情况下,选择高U的矿物分析是为了提高仪器测试精度,但随着技术的进步和年代学理论的发展,人们可以对单个颗粒的锆石乃至锆石的微区分析获得足够高精度的年龄(Krogh,1973),然而不谐和的年龄带来多解性。早期研究认识到可以用磁性的强弱对锆石颗粒进行筛选,带一定磁性的锆石具有更高的U含量而通常给出不谐和的U-Pb年龄,可以获得谐和U-Pb年龄的结晶完好锆石是无磁性的,通过磁分选后的样品分析获得的U-Pb谐和度有所改善(Silver and Deutsch,1963; Krogh,1975,1982a)。Krogh(1982b)首次提出了空蚀法(air abration),通过物理磨蚀去掉锆石颗粒的外层,剩余的中间部分可以获得更为谐和的年龄。这个方法成为之后近20余年TIMS锆石U-Pb定年常用流程,直到Mattinson(2005)提出了化学溶蚀法(chemical abration-CA-TIMS)所取代。CA-TIMS方法首先将锆石在约1100℃高温下煅烧48 h,之后采取分步溶解,剔除前面几段溶解部分,后面阶段可以获得非常谐和的U-Pb体系。笔者曾将一个“高U效应”显著的花岗岩锆石样品进行了同样的热处理,之后重新进行离子探针测试,发现“高U效应”丝毫没有减弱的现象。前人做过更为复杂的实验,以高度损伤的锆石为初始材料,经过多个温度段的热处理,发现~1300℃以下(15 h)不能完全愈合晶格,“高U效应”仍存在,1400℃以上晶格可愈合,但Pb将挥发殆尽(McLaren et al.,1994;Nasdala et al.,2002)。可见这个步骤对离子探针分析U-Pb定年并不见效,有效的是经热处理后的锆石阴极发光图像较未处理的锆石要清晰很多。
对于锆石损伤程度的识别有多种方法,最常用的有X射线衍射测试晶胞参数、拉曼光谱分析特征峰变化、透射电镜观察晶格完整性等。锆石的拉曼光谱最特征的峰为350 cm-1、430 cm-1和1008 cm-1左右,分别对应锆石硅氧四面体的Eg(υ4)和B1 g(υ3)方式的内部振动(Dawson et al.,1971)。锆石的拉曼光谱峰与锆石的蜕晶化程度存在相关性,随着锆石蜕晶化程度的加深,锆石各拉曼谱峰都会向低波数方向位移,且半高宽变大(Nasdala et al.,1995; 程昊等,2002)。蜕晶化使得锆石晶体结构有序性遭到破坏,硅氧四面体内和硅氧四面体之间的键长、键角变得不规则,导致半高宽的增大。而谱峰漂移指示了锆石晶格的扩张,原子间距变大。
目前锆石阴极发光图像已经是微区定年前必做分析,高损伤锆石的阴极发光图像上大多模糊不清,高U含量部位在阴极发光图像上显示为深黑色,避免选择这样的部位可以很大程度上避免“高U效应”。然而锆石的阴极发光的强弱不都是U含量引起的,高损伤锆石未必U含量很高,也可以是非常古老的锆石,确认锆石的损伤状态,锆石的拉曼光谱分析更为简单有效(Nasdala et al.,1995,2001; White and Ireland,2012; Gao et al.,2014)。
3.2 采用其他矿物锆石的U-Pb体系具有相当的矛盾性,一方面即使经过高温变质或熔融,锆石仍可能保留原有年龄信息,但另一方面,放射性损伤积累又使得锆石在低温条件下就可能发生严重的Pb丢失。相对锆石而言,斜锆石、独居石、磷钇矿、榍石、磷灰石等矿物放射性损伤易于愈合,一般不会造成严重的放射性损伤而发生显著Pb丢失,且目前已经成为离子探针U-Pb定年的对象(李秋立等,2013;李秋立,2015)。如对高分异花岗岩定年,高U锆石往往不易于获得理想结果,而独居石和磷钇矿则更为适用(刘志超等,2011;Li et al.,2013)。Rasmussen等(2013)对非洲南部一古元古代地层中经历了低级变质作用的火山灰定年工作中发现,锆石发生了严重Pb丢失,而榍石的微区U-Pb定年获得了记录早期岩浆作用和后期低级变质作用两期事件的谐和年龄。笔者对华北中元古代下马岭组辉绿岩中锆石和斜锆石做过离子探针U-Pb分析,发现斜锆石仅仅发生了极少量的Pb丢失,而锆石的放射成因Pb大多已经丢失了80%以上。可见,选择适宜的矿物是获得理想结果的前提。
4 小结离子探针锆石U-Pb定年发生的“高U效应”使得U-Pb表观年龄变老,但部分样品也会同时受Pb丢失影响而变小,对于单个高U锆石测点来说,离子探针U-Pb年龄偏差较大,需要根据一组高U锆石测点U-Pb年龄和U含量的相关性给出更为合理的年龄结果。锆石的“高U效应”源于蜕晶化和/或后期热愈合使得锆石处于晶态SiO2、ZrSiO4和无定形SiO2的混合状态,U和Pb在不同基体中发生了分异,离子探针激发过程中U-Pb离子化效率相对晶态标准锆石存在显著差异而导致。测试过程中应尽量避免高U锆石的测试,可根据CL图像做筛选。如果一个样品基本都是高U锆石,建议用同样品的其他矿物,如独居石、磷钇矿、榍石等代替。
| [1] | Black L P, Kinny P D, Sheraton J W. 1991. The difficulties of dating mafic dykes: An Antarctic example. Contributions to Mineralogy and Petrology, 109(2): 18-194 |
| [2] | Black L P, Kamo S L, Allen C M, Davis D W, Aleinikoff J N, Valley J W, Mundil R,Campbell I H, Korsch R J, Williams I S, Foudoulis C. 2004. Improved 206Pb/238U microprobe geochronology by the monitoring of a trace-element-related matrix effect: SHRIMP, ID-TIMS, ELA-ICP-MS and oxygen isotope documentation for a series of zircon standards. Chemical Geology, 205(1-2): 115-140. |
| [3] | Chakoumakos B C, Murakami T, Lumpkin G R, Ewing R C. 1987. Alpha-decay induced fracturing in zircon: The transition from the crystalline to the metamict state. Science, 236(4808): 1556-1559 |
| [4] | Dawson P, Hargreave M M, Wilkinson G D. 1971. The vibrational spectrum of zircon(ZrSiO4). Journal of Physics C: Solid State Physics, 4(2): 240-255 |
| [5] | Ewing R C, Meldrum A, Wang L M, Weber M J, Corrales L R. 2003. Radiation effects in zircon. Reviews in Mineralogy and Geochemistry, 53(1): 387-425 |
| [6] | GaoY Y, Li X H, Griffin W L, O'Reilly S Y, Wang Y F. 2014. Screening criteria for reliable U-Pb geochronology and oxygen isotope analysis in uranium-rich zircons: A case study from the Suzhou A-type granite, SE China. Lithos, 192-195: 180-191 |
| [7] | Ireland T R, Williams I S. 2003. Considerations in zircon geochronology by SIMS. Reviews in Mineralogy and Geochemistry, 53(1): 215-241 |
| [8] | Jackson S E, Pearson N J, Griffin W L, Belousova E A. 2004. The application of laser ablation-inductively coupled plasma-mass spectrometry to in situ U-Pb zircon geochronology. Chemical Geology, 211(1-2): 47-69 |
| [9] | Krogh T E. 1973. A low contamination method for the hydrothermal decomposition of zircon and extraction of U and Pb for isotopic age determinations. Geochimica et Cosmochimica Acta, 37(3): 485-494 |
| [10] | Krogh T E. 1975. Differential dissolution of altered and metamict zircon. EOS Transactions, 56(6): 472-473 |
| [11] | Krogh T E. 1982a. Improved accuracy of U-Pb zircon dating by selection of more concordant fractions using a high gradient magnetic separation technique. Geochimica et Cosmochimica Acta, 46(4): 631-635 |
| [12] | Krogh T E. 1982b. Improved accuracy of U-Pb zircon ages by the creation of more concordant systems using an air abrasion technique. Geochimica et Cosmochimica Acta, 46(4): 637-649 |
| [13] | Kusiak M A, Whitehouse M J, Wilde S A, Nemchin A A, Clark C. 2013. Mobilization of radiogenic Pb in zircon revealed by ion imaging: Implications for early Earth geochronology. Geology, 41(3): 291-294 |
| [14] | Leech M L. 2008. Does the Karakoram fault interrupt mid-crustal channel flow in the western Himalaya?. Earth and Planetary Science Letters, 276(3-4): 314-322 |
| [15] | Li Q L, Li X H, Liu Y, Tang G Q, Yang J H, Zhu W G. 2010. Precise U-Pb and Pb-Pb dating of Phanerozoic baddeleyite by SIMS with oxygen flooding technique. Journal of Analytical Atomic Spectrometry, 25(7): 1107-1113 |
| [16] | Li Q L, Li X H, Lan Z W, Guo C L, Yang Y N, Liu Y, Tang G Q. 2013. Monazite and xenotime U-Th-Pb geochronology by ion microprobe: Dating highly fractionated granites at Xihuashan tungsten mine, SE China. Contributions to Mineralogy and Petrology, 166(1): 65-80 |
| [17] | Li X H, Liu Y, Li Q L, Guo C H, Chamberlain K R. 2009. Precise determination of Phanerozoic zircon Pb/Pb age by multi-collector SIMS without external standardization. Geochemistry, Geophysics, Geosystems, 10(4): Q04010, doi: 10.1029/2009GC002400 |
| [18] | Mattinson J M. 2005. Zircon U-Pb chemical abration("CA-TIMS")method: Combined annealing and multi-step partial dissolution analysis for improved precision and accuracy of zircon ages. Chemical Geology, 220(1-2): 47-66 |
| [19] | McLaren A C, Gerald J D F, Williams I S. 1994. The microstructure of zircon and its influence on the age determination from Pb/U isotopic ratios measured by ion microprobe. Geochimica et Cosmochimica Acta, 58(2): 993-1005 |
| [20] | Meldrum A, Boatner L A, Weber W J, Ewing R C. 1998. Radiation damage in zircon and monazite. Geochimica et Cosmochimica Acta, 62(14): 2509-2520 |
| [21] | Murakami T, Chakoumakos B C, Ewing R C, Lumpkin G R, Weber W J. 1991. Alpha-decay event damage in zircon. American Mineralogist, 76(9-10): 1510-1532 |
| [22] | Nasdala L, Irmer G, Wolf D. 1995. The degree of metamictization in zircon: A Raman spectroscopic study. European Journal of Mineralogy, 7(3): 471-478 |
| [23] | Nasdala L, Wenzel M, Vavra G, Irmer G, Wenzel T, Kober B. 2001. Metamictisation of natural zircon: Accumulation versus thermal annealing of radioactivity-induced damage. Contributions to Mineralogy and Petrology, 141(2): 125-144 |
| [24] | Nasdala L, Lengauer C L, Hanchar J M, Kronz A, Wirth R, Blanc P, Kennedy A K, Seydoux-Guillaume A M. 2002. Annealing radiation damage and the recovery of cathodoluminescence. Chemical Geology, 191(1-3): 121-140 |
| [25] | Nasdala L, Hanchar J M, Kronz A, Whitehouse M J. 2005. Long-term stability of alpha particle damage in natural zircon. Chemical Geology, 220(1-2): 83-103 |
| [26] | Nasdala L, Hofmeister W, Norberg N, Mattinson J M, Corfu F, Dörr W, Kamo S L, Kennedy A K, Kronz A, Reiners P W, Frei D, Kosler J, Wan Y S, Götze J, Häger T, Kröner A, Valley J W. 2008. Zircon M257-a homoegenous natural reference material for the ion microprobe U-Pb analysis of zircon. Geostandards and Geoanalytical Research, 32(3): 247-265 |
| [27] | Nasdala L, Hanchar J M, Rhede D, Kennedy A K, Váczi T. 2010. Retention of uranium in complexly altered zircon: An example from Bancroft, Ontario. Chemical Geology, 269(3-4): 290-300 |
| [28] | Rasmussen B, Fletcher I R, Muhling J R. 2013. Dating deposition and low-grade metamorphism by in situ U-Pb geochronology of titanite in the Paleoproterozoic Timeball Hill Formation, southern Africa. Chemical Geology, 351: 29-39 |
| [29] | Silver L T, Deutsch S. 1963. Uranium-lead isotope variations in zircons: A case study. The Journal of Geology, 71(6): 721-758 |
| [30] | Sláma J, Košler J, Condon D J, Crowley J L, Gerdes A, Hanchar J M, Horstwood M S A, Morris G A, Nasdala L, Norberg N, Schaltegger U, Schoene B, Tubrett M N, Whitehouse MJ. 2008. Plešovice zircon: A new natural reference material for U-Pb and Hf isotopic microanalysis. Chemical Geology, 249(1-2): 1-35 |
| [31] | Stern R A, Amelin Y. 2003. Assessment of errors in SIMS zircon U-Pb geochronology using a natural zircon standard and NIST SRM 610 glass. Chemical Geology, 197(1-4): 111-142 |
| [32] | Valley J W, Cavosie A J, Ushikubo T, Reinhard D A, Lawrence D F, Larson D J, Clifton P H, Kelly T F, Wilde S A, Moser D E, Spicuzza M J. 2014. Hadean age for a post-magma-ocean zircon confirmed by atom-probe tomography. Nature Geoscience, 7(3): 219-223, doi: 10.1038/ngeo2075 |
| [33] | Weber W J, Ewing R C, Wang L M. 1994. The radiation-induced crystalline to amorphous transition in zircon. Journal of Materials Research, 9(3): 688-698 |
| [34] | White L T, Ireland T R. 2012. High uranium matrix effect in zircon and its implications for SHRIMP U-Pb age determinations. Chemical Geology, 306-307: 78-91 |
| [35] | Whitehouse M J, Kumar G R R, Rimsa A. 2014. Behaviour of radiogenic Pb in zircon during ultrahigh temperature metamorphism: An ion imaging and ion tomography case study from the Kerala Khondalite Belt, southern India. Contributions to Mineralogy and Petrology, 168: 1042 |
| [36] | Williams I S, Compston W, Black L P, Ireland T R, Foster J J. 1984. Unsupported radiogenic Pb in zircon: A cause of anomalously high Pb-Pb, U-Pb and Th-Pb ages. Contributions to Mineralogy and Petrology, 88(4): 322-327 |
| [37] | Williams I S, Hergt J M. 2000. U-Pb dating of Tasmanian dolerites: A cautionary tale of SHRIMP analysis of high-U zircon. In: Woodhead J D, Hergt J M, Noble W P, eds. Beyond 2000: New Frontiers in Isotope Geoscience: Lorne, Abstract Proceedings, 185-188 |
| [38] | Wiedenbeck M, Alle P, Corfu F, Griffin W L, Meier M, Oberli F, Vonquadt A, Roddick J C, Speigel W. 1995. Three natural zircon standards for U-Th-Pb, Lu-Hf, traceelement and REE analyses. Geostandards Newsletter, 19(1): 1-23 |
| [39] | 程昊, 陈道公, Deloule E, 吴元保. 2002. 变质锆石拉曼光谱研究: 以大别造山带为例. 矿物学报, 22(4): 353-358 |
| [40] | 李秋立, 杨蔚, 刘宇, 唐国强, 郝佳龙, 张建超, 胡森, 赵旭晁, 陈雅丽, 储雪蕾, 王英, 蒋云, 张爱铖, 徐伟彪, 林杨挺, 李献华. 2013. 离子探针微区分析技术及其在地球科学中的应用进展. 矿物岩石地球化学通报, 32(3): 310-327 |
| [41] | 李秋立. 2015. U-Pb定年体系特点和分析方法解析. 矿物岩石地球化学通报, 34(3): 491-500 |
| [42] | 刘志超, 吴福元, 郭春丽, 赵子福, 杨进辉, 孙金凤. 2011. 磷钇矿U-Pb年龄激光原位ICP-MS测定. 科学通报, 56(33): 2772-2781 |
| [43] | 杨亚楠, 李秋立, 刘宇, 唐国强, 凌潇潇, 李献华. 2014. 离子探针锆石U-Pb定年. 地学前缘, 21(2): 81-92 |
 2016, Vol. 35
2016, Vol. 35

