2. 中国科学院大学, 北京 100049;
3. 中国地质大学(北京), 北京 100083
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Earth Sciences and Resources, China University of Geosciences(Beijing), Beijing 100083, China
利用多接收杯电感耦合等离子质谱仪(MC-ICP-MS)和热电离质谱仪(TIMS)测定同位素组成时,测量值与真实值之间存着一定的偏差(Mass bias),该偏差校正的好坏影响着测试结果的准确度和精密度(Woodhead and Hergt,1997; Habfast,1998; Albarède and Beard,2004)。质量歧视的大小与同位素的质量差(ΔM)成一定的函数关系,故称之为仪器的同位素质量分馏。目前,同位素质量分馏的校正通常有3种方法(Yang,2009; 李津等,2011a,2011b):标准样品交叉法(st and ard sample bracketing,SSB)(Zhu et al.,2000,2002)、元素外标法(element doping,ED)(Maréchal et al.,1999; White et al.,2000)和同位素双稀释剂法(double spike,DS)(Dodson,1963; Hamelin et al.,1985; Johnson et al.,1999; Johnson and Beard,1999; Siebert et al.,2001; Rudge et al.,2009)。前人研究表明,同位素双稀释剂法校正后获得数据的准确度和精密度都相对较高,已成为其他2种方法校正评价的对比基准。
同位素双稀释剂法最早由Dodson于1963年首次提出。随后被广泛用于稳定同位素的质量分馏校正,特别是在非传统稳定同位素地球化学领域,如在Ca(Heuser et al.,2002; Gopalan et al.,2006),Cr(Zink et al.,2010),Fe(Johnson and Beard,1999; Schoenberg and von Blanckenburg,2005),Ni(Gall et al.,2012),Zn(Arnold et al.,2010),Se(Johnson et al.,1999; Zhu et al.,2008),Mo(Siebert et al.,2001; 李津等,2011a,2011b),Cd(Ripperger et al.,2007),Hg(Mead and Johnson,2010)等的研究。由于同位素双稀释剂法涉及复杂的数学处理,其数据迭代方法因研究者不同而存在差异,使得其在国际上存在3种主流算法:① 以Rudge等(2009)为代表的牛顿迭代算法,其将指数律外加混合模型建立一个非线性方程组,并通过牛顿迭代的方式求解,得到精确的同位素比值; ② Siebert等的几何迭代算法(Siebert et al.,2001; Millet et al.,2012),主要内容是在几何的三维空间内求解线与面之间的交点来实现对质量歧视的校正; ③ Johnson等的鸟巢迭代算法(Johnson et al.,1999; Zhu et al.,2008; Fantle and Bullen,2009; Mann et al.,2012),通过2个等式迭代剥离出稀释剂与样品的同位素组成来实现测试数据分馏的校正。影响双稀释剂法使用的关键问题在于: ①难以准确掌握两单稀释剂之间(λ)以及双稀释剂与样品之间的最优配比值(p),此参数的获取可借助实测数据分析(Siebert et al.,2001)或计算机数值模拟(Rudge et al.,2009; John,2012);②双稀释剂同位素组成的准确标定,标定结果的质量会直接影响到双稀释剂法校正数据结果的精密度和准确度。为了能够有效的评估误差增量的大小,Hamelin等(1985)在Cumming(1973)的工作基础上提出了线性误差增量模型,随后Rudge等(2009)将其推广到非线性的误差增量估算。此外,Mel'nikov(2005),Fantle和Bullen(2009)等运用Monte-Carlo的方法评估了DS法校正过程的误差增量。随着国外双稀释剂法的普及,国内研究人员也展开了相应的工作,如对Cr(李理等,2009),Se(Zhu et al.,2008),Pb(常向阳,1999; 王林森和张利,2003),Mo(李津等,2011a,2011b)等同位素的双稀释剂法测定,这些元素同位素双稀释剂法的使用为国内同位素双稀释剂技术的进一步发展奠定了良好的基础。
本文在综合分析Hofmann(1971),Johnson和Beard(1999)和Siebert等(2001)等学者的同位素双稀释剂算法的基础上,以Siebert等人的双稀释剂算法为出发点,对同位素双稀释剂法的数学原理、双稀释剂的选择,两单稀释剂之间以及双稀释剂与样品之间的配比优化、双稀释剂同位素组成的标定等方面进行了全面详细的阐述,以期为国内学者对同位素双稀释剂法的原理与应用有更为深入的了解和认识。
1 双稀释剂法的数学原理 1.1 同位素混合模型与分馏规律双稀释剂法即为向样品溶液中加入已知同位素比值的双稀释剂,经仪器分析得到混合溶液(样品+双稀释剂)中的3组同位素比值,由同位素混合模型 及仪器的质量分馏规律建立相应的数学模型,并对测量值进行迭代运算,剔除稀释剂组成后得到自然样品的真实同位素组成。
公式(1)给出了双稀释剂与自然样品混合的基本公式,其中Ni、 Mi、 Si分别为样品、 样品+双稀释剂、 双稀释剂中第i个同位素与参考同位素(k)的真实比值,如(82Se/76Se)sample、(82Se/76Se)mix、(82Se/74Se)spike。
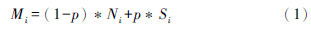
式中:p为(Ri,k)spike与(Ri,k)mix之比,Ri,k即为第i个同位素与参考同位素(k)的比值,具体如(82Se/76Se)spike与(82Se/76Se)mix之比,76Se为参考同位素。
20世纪90年代以前,部分学者如Dodson(1963,1970)、Gale(1970)、Hamelin等(1985)使用线性分馏律对质谱的质量歧视进行校正,然而Russell等(1978)、 Hart和Zindler(1989)使用TIMS对 Ca同位素的质量分馏进行研究时发现指数律的拟合度最好。指数律的数学表达如下(Albaréde and Beard,2004):

式中:mi为仪器对混合溶液的测量值,Mi为被测元素中第i个同位素的原子质量,Mk为参考同位素的原子质量,β为仪器的质量分馏因子。
假定样品在自然界中的分馏也遵循指数分馏规律,分馏因子为α,则样品相对于标准物质的分馏规律为:

式中:ni为标准溶液中第i个同位素与参考同位素的比值。
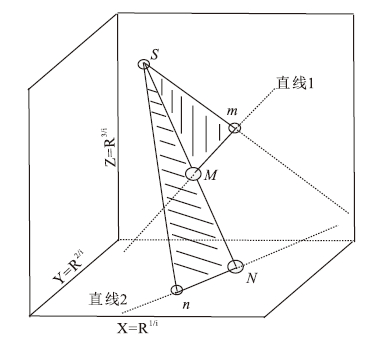
1.2 测量数据的迭代原理本文讨论的迭代算法是Siebert等(2001)在Hofmann(1971)和Johnson和Beard(1999)的基础上发展起来的一种双稀释剂的数值算法,主要原理是在三维空间内求解面与线的交点来获得混合样品和自然样品的真实同位素比值。其原理如 图 1,X、Y、Z为某元素的3组同位素比值,若以硒(Se)同位素为例,X=82Se/76Se、 Y=74Se/76Se、Z=77Se/76Se。S、N、M分别为双稀释剂、样品、混合样品的真实同位素比值,m为混合样品的测量值,n为标准的测量值。
|
图 1 同位素双稀释剂原理图 Fig. 1 A schematic diagram showing mathematical principle of the double spike |
根据同位素线性混合模型,M必在S-N-n所属的平面上,连接M-m的直线1即为混合样品的指数分馏线,实际上它并不是一条直线,此处为了便于求解,用直线近似的替代,所以直线1与平面S-N-n相交于一点M,只需求解该点的坐标值,即可得到混合样品的真实同位素比值,同样,求出直线2与平面S-M-m的交点S,就可获得样品的真实同位素比值。
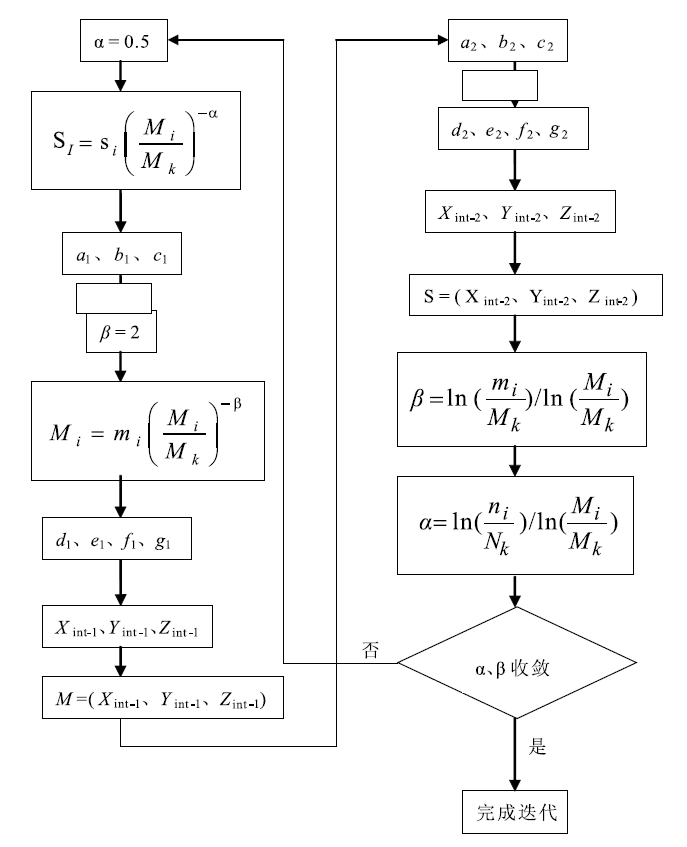
迭代思想如 图 2,第一步是假设α等于某值(Siebert et al.,2001),本文取值为0.5,S、n的同位素比值已知,由公式(2)得到N的同位素组成,根据已知的3点可以解析出平面S-N-n。解析步骤为:
|
图 2 几何迭代算法的流程图,经两步迭代运算直至α、β值收敛 Fig. 2 A flow chart of the geometric iteration method for the double spike, displaying two steps iteration until the value of α and β convergence |
首先将平面S-N-n定义为:Z=a1X+b1Y+c1,并将Z、X、Y3点的同位素比值代入该平面的数学表达式中可解析出a1、b1、c1的值,具体的计算公式如文献所述的表示如下:
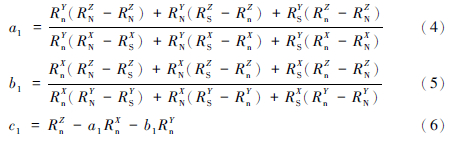
式中:R代表某同位素的比值,X、Y、Z为1/i、2/i、3/i,如图 1其中1、2、3为某元素的3个同位素,i为参考同位素,如Se,1、2、3可为74Se、77Se、78Se,i为76Se。
假设β为某范围值,本文取值为2,根据公式(1)计算出M的同位素组成,由已知的m和计算得到的M可以解析出直线1,其中直线1在3围空间中可表达为:Z=d1X+e1,和Z=f1Y+g1。将m和M的同位素比值代入直线1的数学表达式中,可得到d1、e1、 f1、 g1的值,其计算公式如下:
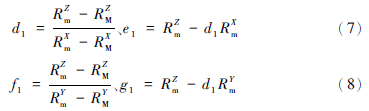
由于平面S-N-n和直线1相交点M,可由Z=a1X+b1Y+c1、Z=d1X+e1和Z=f1Y+g1组成一个简单的线性方程组,解的交点坐标值(Xint-1,Yint-1,Zint-1),获得新的M值,具体表达式为:
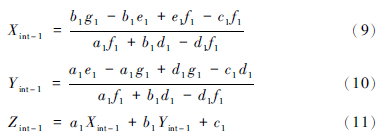
第二步:由S、m和上前一步计算得到的M值可解析出平面S-m-M,平面S-m-M的数学表达式为:Z=a2X+b2Y+c2,将Z、X、Y 3点的同位素比值代入S-m-M平面的表数学达式中可得到a2、b2、c2的值。
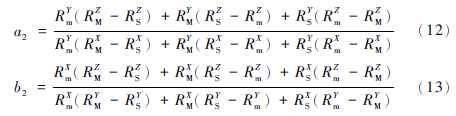

再由(3)式计算得N和标准值n可确定直线2,直线2在三维空间中可表达为:Z=d2X+e2,和Z=f2Y+g2。其中:
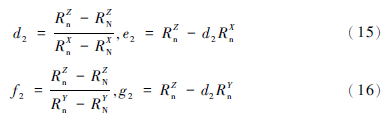
通过简单的计算就可以得到平面S-m-M与直线2的交点值(Xint-2,Yint-2,Zint-2),用此交点值代替N,得到新的N。其中Xint-2,Yint-2,Zint-2的表达式为:
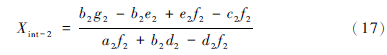
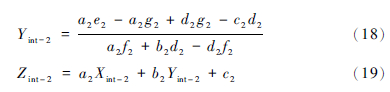
由公式1和2计算出新的α、 β值,重复第一步和第二步,直至α和β值收敛。该方法涉及到数学中的解析几何知识,固可称之为几何迭代。
2 同位素双稀释剂的选择原则双稀释剂选择的过程,如Se具有74Se、76Se、77Se、78Se、80Se、82Se 6种同位素,根据概率统计学中重组的原则,两两组合为C26=15,因此双稀释剂的选择具有15种,能够用于迭代校正同位素组合有C26×C24=90种。在众多的双稀释剂组合中,并非每种组合都是可行和适合用于同位素校正的双稀释剂,其需要通过相关的原则和方法找出最佳的组合。
双稀释的定性选择一般遵循Siebert等(2001),Johnson等(1999)提出的原则,即:①组成双稀释的2同位素在自然样品中丰度较低,当向样品中加入双稀释剂时可达到稀释的目的,其在计算中的表现为代入的误差较小,校正得到的数据准确度和紧密度都较高;②在仪器测定时所受异位素或同质的多原子分子的干扰要小。③单稀释剂价格与其在实验室条件下纯化富集的容易度成正比关系,因此在某些特定的条件下,选择易于纯化的稀释剂较好。定量的选择即为每组双稀释剂在最优配比下对仪器的质量分馏校正所产生的误差增量偏小,同时要求在两单稀释剂之间(λ)以及双稀释剂与样品之间(p)的最优配比值附近较大区间内趋于平稳(Rudge et al.,2009; John,2012; 朱建明等未发表的数据)。
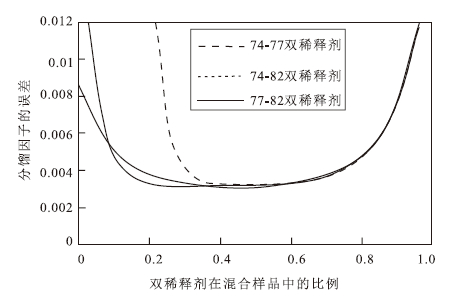
在自然样品中,74Se(0.889%)、76Se(9.366%)77Se(7.635%)、82Se(8.731%)的丰度较低,MC-ICPMS硒同位素比值测定时,76Se+易受 40 Ar 36 Ar+、AsH+、Ge+等离子的干扰,因此在双稀释剂选择时,76Se不予考虑,74Se、77Se、82Se 3个同位素可组成74Se-77Se、 74Se-82Se、77Se-82Se 3对双稀释剂。 图 3分别展示了74Se-77Se、74Se-82Se、77Se-82Se双稀释剂的组成在最优配比下校正的误差曲线图。3种稀释剂组合校正后自然分馏因子的误差值相当,74Se-77Se双稀释剂在与自然样品混合时的配比选择范围较窄,74Se-82Se、77Se-82Se在 图 3中的误差曲线形态相似,误差值变化平缓且范围较宽,在实验操作中可避免由于双稀释剂与样品配比的过高(Over spike)或过低(Under spike)造成误差的巨变。总之,74Se-82Se双稀释剂同位素分馏校正时的误差较小,双稀释剂与自然样品混合时的配比选择范围最宽,可作为最优的双稀释剂组合。
|
图 3 3种不同稀释剂校正后α的误差图 Fig. 3 The curvy graph showing errors in alpha for three different double spikes |
双稀释剂技术应用的关键在于双稀释剂中两同位素比值(λ)以及其与样品之间的配比(p)值的优化,该优化的过程可由误差的计算予以实现。Cumming(1973)指出,误差大小与λ值和p值有关。当λ、p值发生变化时,校正过程的误差增量的大小也随之变化。双稀释间以及双稀释剂与样品间的配比的优化即为寻找一个恰当的 λ值和p值,使质量分馏校正后的误差降到最小。目前有2种方法可获得最佳的λ值和p值,(1)为测试不同λ、p值的混合溶液,通过校正后误差增量的大小来判断λ、p 组合的好坏(Cumming,1973);(2)为计算机数值模拟,即将预设的误差模型与迭代公式结合求得校正后的误差增量(Galer,1999; Rudge et al.,2009; John,2012)。
John(2012)使用几何迭代算法对S、Ca、Fe、Ni、Zn等33种元素的双稀释剂λ、p值进行了优化。其步骤是,首先建立误差模型。质谱误差的来源一般有:①电阻器噪声(Resistor noise or Johnson noise); ②散粒效应(Shot noise); ③同质异位数; ④多原子分子的干扰。John将各个效应的误差贡献量定义为:
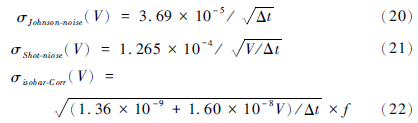
多原子分子的干扰随时间不断的在变化,难以用公式的形式予以估算,因此此处不予考虑。误差模型可简化为:
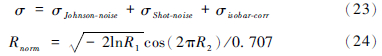
(24)式中: R1、R2为-1至1内均匀分布的数,Rnorm为一组正态分布的数据,标准偏差等于1。
其次,将(23)和(24)式与仪器接收到的离子束信号强度(V)值结合,得到仪器的测量值,即为Rnorm与V相乘,并结合(23)式的误差值模拟出测量值。测量值经几何迭代(图 2)校正,计算出分馏因子的误差或某同位素比值(82Se/76Se)的误差。观察λ、p值与误差值的关系,当误差处于最小值时可得到最优的λ、p值。
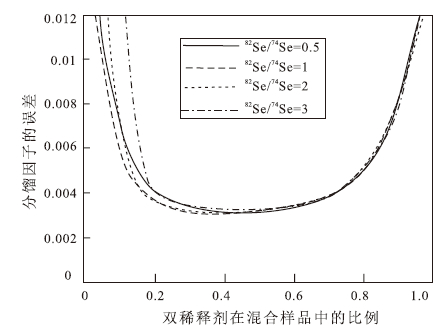
图 4呈现了74Se-82Se双稀释剂的优化结果,当两单稀释剂之比,即82/74=1或 2时,自然分馏因子α的误差一致,而82/74=0.5或3时,误差值的最优范围在缩小,因此最优的82/74值在1~2内变动。在实际应用时,82/74的值可扩展到小于1或大于2,对结果影响不大。当 p值从0变到1时,在α中所产生的误差大小呈现U型的曲线,图 4中当 82/74=1,可得到p的最优变化范围,从0.25变化到0.55,在此范围内α的误差相对较小。
|
图 4 λ和p值的误差增量图 Fig. 4 Plot of errors in alpha against various values of λ and p |
商家提供稀释剂的同位素组成一般不是它们的准确组成,或者由于其他原因如衰变或人为污染导致了原来的同位素组成发生了微小变化。因此,在实验前必须对双稀释剂同位素的组成予以标定(Hamelin et al.,1985; Markey et al.,2003; Rudge et al.,2009),否则校正的结果将会出现较大偏差,影响数据的准确性。目前双稀释剂同位素组成的标定方法有以下几种:
4.1 标准样品交叉法标定利用已知同位素组成的标准溶液进行反复测定,观察仪器的漂移和稳定性,在仪器较好状态下,分别就所需要标定的双稀释剂与标样进行交叉测定,由(2)式分别计算出其相应仪器同位素分馏因子α1、α2,由α1、α2算出平均分馏因子α,后将α与双稀释剂和标样测试测试结果代入(2)式中进行校正,得到真实的同位素组成(Albarède and Beard,2004)。这种方法虽然不适合于双稀释剂中所有同位素组成的精确标定,且有可能因为双稀释剂同位素组成与标准的组成相差太大,形成较大的误差,但对双稀释剂中的两稀释剂主成分而言,其标定结果是相对可靠的。
4.2 元素内标法标定往双稀释剂和标准溶液分别加入与待测元素质量相近的已知其同位素组成的某种同位素标准,如Siebert等(2001),李津等(2011b)在对97Mo-100Mo双稀释剂和Mo的标准溶液的同位素比值标定时,加入了104Pd/102Pd,并假设Mo与Pd的仪器同位素分馏效应相同。由于加入的元素的同位素比值已知,后通过仪器的测试得到测量值,由(2)式计算出分馏因子α,将α值与双稀释剂和标准溶液的同位素测量值代入(2)式中得到真实的同位素比值。数学表达如李津等(2011)对Mo的同位素比值标定:
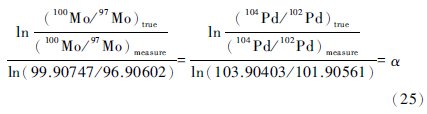
(25)式中:(104Pd/102Pd)true为加入元素同位素比值的真实值,为测量值(104Pd/102Pd)measure,都已知,从而得到α;(100Mo/97Mo)measure 为稀释剂和标样的同位素比值的测量值,α代入左式,求得(100Mo/97Mo)true。然后再假设该值为定值,去求得其他同位素对的比值。
4.3 同位素双稀释剂组成的确定在双稀释剂的标定过程中,最重要的环节是最后一步,也就是把双稀释剂与已知同位素组成的标准溶液混合,对其测量值进行上述小节描述的迭代计算,获得质量分馏校正后的真值。此时,同位素标样的同位素组成最好是接近该同位素的自然丰度,使得其标样中某对同位素的比值为0或在要求的一定范围内,但该步的最终完成对同位素双稀释剂制备者有相当高的经验和对仪器熟悉程度的要求,稀释剂的组成一旦确定且在相当长时间内进行测试证明同位素标准比值的稳定,也就意味着最终完成了同位素双稀释剂组成的标定(Cooper et al.,1969; Rudge et al.,2009; Neymark et al.,2014)。
5 双稀释剂法的优缺点双稀释剂法的同位素质量分馏校正,相对于其他方法 SSB、Element doping具有许多的优势:①仪器的同位素分馏校正值的准确度及精密度较高,可用于自然界小范围的同位素变化的研究;②可同时校正化学纯化过程和仪器的同位素质量分馏;③双稀释剂法可使待测元素获得高准确度的浓度值;④可以缓冲或降低同量异位素、多原子分子或一些非光谱性的干扰(Siebert et al.,2001);⑤可用于低浓度样品的同位素组成测试,测试时所需样品量最少;⑥可获得自然样品的同位素组成。
Mead和Johnson(2010)对Hg的同位素比值测定中,指出同位素双稀释剂法校正优于Tl元素内标及交叉法对Hg同位素的分馏校正。但其也存在着一些缺点或者说是难点:①研究者必须要熟练的掌握2稀释剂之间的配比以及双稀释剂与样品溶液间配比情况;②需要对双稀释剂进行精确的标定,否则会代入不必要的误差。③双稀释剂只能用于具有4个或以上同位素的元素,人工制造稀释剂的添加(如233U-236U)是同位素双稀释剂的个案或特例;④对于高纯的同位素稀释剂来说,价格昂贵。总的来说,同位素双稀释剂制备和组成的标定在同位素双稀释剂法使用前期需要一定机时、经费和人力的投入(Mead and Johnson,2010)。
6 结论同位素双稀释剂法在国际上已经过五十多年的发展,现已较为成熟。然而,对于国内同行的研究者来说,由于其数学运算的复杂还未到完全熟练应用的阶段。随着多接收杯电感耦合等离子质谱(MC-ICP-MS)的广泛使用和普及,在今后一段时间内,相信同位素双稀释剂法在非传统稳定同位素的分析技术中将占有举足轻重的地位。同位素双稀释剂法是属于已知同位素对比值的内校正方法,现已有学者在选择合适目标稀释剂的前提下,利用同位素双稀释剂法进行非传统稳定同位素的非质量分馏研究,这极可能成为双稀释剂法未来应用的新方向。目前,国际上双稀释法的迭代方式主要有3种,即Rudge等为代表的牛顿迭代算法、 Siebert等的几何迭代算法和Johnson等的鸟巢迭代算法。本文对Siebert等的几何迭代算法进行了详细的描述,其主要思路是在三维空间内求解面与线的交点来获取混合样品和自然样品的真实同位素比值。双稀释剂法使用的关键在于获取两单稀释剂间以及稀释剂与样品之间的最优配比值,获取的一般途径有实测数据,查看不同λ、p值混合下校正得到数据的准确度和精密度,其次是通过计算机数值模拟,将预设误差模型与迭代算法结合、模拟出自然分馏因子或某同位素比值的误差值,通过误差增量的大小判断最优的λ和p值。双稀释剂的标定流程较为简单,但在实际的操作中,需要有经验者的指导和一定机时、经费与人力的投入。
致谢: 本论文的撰写和学术思想得益于美国伊利诺伊大学香槟-厄巴纳分校地质系Johnson教授的鼓励和讨论,也得到中国地质科学院同位素地球化学实验室朱祥坤研究员和李津副研究员的帮助,中科院广州地球化学研究所张兆峰研究员提出了宝贵意见,谨此致谢!
| Albarède F, Beard B. 2004. Analytical methods for non-traditional isotopes. Reviews in Mineralogy & Geochemistry, 55(1): 113-152 |
| Arnold T, Schönbächler M, Rehkämper M, Dong S, Zhao F J, Kirk G J, Coles B J, Weiss D J. 2010. Measurement of zinc stable isotope ratios in biogeochemical matrices by double-spike MC-ICPMS and determination of the isotope ratio pool available for plants from soil. Analytical and Bioanalytical Chemistry, 398(7-8): 3115-3125 |
| Cooper J A, Reynolds P H, Richards J R. 1969. Double-spike calibration of the broken hill standard lead. Earth and Planetary Science Letters, 6(6): 467-478 |
| Cumming G L. 1973. Propagation of experimental errors in lead isotope ratio measurements using the double spike method. Chemical Geology, 11(3): 157-165 |
| Dodson M H. 1963. A theoretical study of the use of internal standards for precise isotopic analysis by the surface ionization technique: Part I-General first-order algebraic solutions. Journal of Scientific Instruments, 40(6): 289-295 |
| Dodson M H. 1970. Simplified equations for double-spiked isotopic analyses. Geochimica et Cosmochimica Acta, 34(11): 1241-1244 |
| Fantle M S. Bullen T D. 2009. Essentials of iron, chromium, and calcium isotope analysis of natural materials by thermal ionization mass spectrometry. Chemical Geology, 258(1-2): 50-64 |
| Gale N H. 1970. A solution in closed form for lead isotopic analysis using a double spike. Chemical Geology, 6: 305-310 |
| Galer S J G. 1999. Optimal double and triple spiking for high precision lead isotopic measurement. Chemical Geology, 157(3-4): 255-274 |
| Gall L, Williams H, Siebert C, Halliday A. 2012. Determination of mass-dependent variations in nickel isotope compositions using double spiking and MC-ICPMS. Journal of Analytical Atomic Spectrometry, 27: 137-145 |
| Gopalan K, Macdougall D, Macisaac C. 2006. Evaluation of a42 Ca-43 Ca double-spike for high precision Ca isotope analysis. International Journal of Mass Spectrometry, 248(1-2): 9-16 |
| Habfast K. 1998. Fractionation correction and multiple collectors in thermal ionization isotope ratio mass spectrometry. International Journal of Mass Spectrometry, 176(1-2): 133-148 |
| Hamelin B, Manhes G, Albarede F, Allegre C J. 1985. Precise lead isotope measurements by the double spike technique: A reconsideration. Geochimica et Cosmochimica Acta, 49(1): 173-182 |
| Hart S R, Zindler A. 1989. Isotope fractionation laws: A test using calcium. International Journal of Mass Spectrometry and Ion Processes, 89(2-3): 287-301 |
| Heuser A, Eisenhauer A, Gussone N, Bock B, Hansen B T, Nägler T F. 2002. Measurement of calcium isotopes(δ44 Ca)using a multicollector TIMS technique. International Journal of Mass Spectrometry, 220(3): 385-397 |
| Hofmann A. 1971. Fractionation corrections for mixed-isotope spikes of Sr, K, and Pb. Earth and Planetary Science Letters, 10(4): 397-402 |
| John S G. 2012. Optimizing sample and spike concentrations for isotopic analysis by double-spike ICPMS. Journal of Analytical Atomic Spectrometry, 27(12): 2123-2131 |
| Johnson C M, Beard B L. 1999. Correction of instrumentally produced mass fractionation during isotopic analysis of Fe by thermal ionization mass spectrometry. International Journal of Mass Spectrometry, 193(1): 87-99 |
| Johnson T M, Herbel M J, Bullen T D, Zawislanski P T. 1999. Selenium isotope ratios as indicators of selenium sources and oxyanion reduction. Geochimica et Cosmochimica Acta, 63(18): 2775-2783 |
| Mann J L, Vocke Jr R D, Kelly W R. 2012. Determination of low-level(sub-microgram)sulfur concentrations by isotope dilution multi-collector inductively couple plasma mass spectrometry using a33S spike and internal normalization for mass bias correction. Rapid Communications in Mass Spectrometry, 26(10): 1175-1180 |
| Maréchal C N, Télouk P, Albarède F. 1999. Precise analysis of copper and zinc isotopic compositions by plasma-source mass spectrometry. Chemical Geology, 156(1-4): 251-273 |
| Markey R, Hannah J L, Morgan J W, Stein H J. 2003. A double spike for osmium analysis of highly radiogenic samples. Chemical Geology, 200(3-4): 395-406 |
| Mead C, Johnson T M. 2010. Hg stable isotope analysis by the double-spike method. Analytical and Bioanalytical Chemistry, 397(4): 1529-1538 |
| Mel'nikov N N. 2005. Errors of the double spiking technique in the isotopic analysis of common lead. Geochemistry International, 43(12): 1228-1234 |
| Neymark L A, Premo W R, Mel'nikov N N, Emsbo P. 2014. Precise determination ofδ88 Sr in rocks, minerals, and waters by double-spike TIMS: A powerful tool in the study of geological, hydrological and biological processes. Journal of Analytical Atomic Spectrometry, 29(1): 65-75 |
| Millet M A. Baker J A. Payne C E. 2012. Ultra-precise stable Fe isotope measurements by high resolution multiple-collector inductively coupled plasma mass spectrometry with a57Fe-58Fe double spike. Chemical Geology, 304: 18-25 |
| Ripperger S, Rehkämper M, Porcelli D, Halliday A N. 2007. Cadmium isotope fractionation in seawater-A signature of biological activity. Earth and Planetary Science Letters, 261(3-4): 670-684 |
| Rudge T J F, Reynolds B C, Bourdon B. 2009. The double spike toolbox. Chemical Geology, 265(3-4): 420-431 |
| Russell W A, Papanastassiou D A, Tombrello T A. 1978. Ca isotope fractionation on the Earth and other solar system materials. Geochimica et Cosmochimica Acta, 42(8): 1075-1090 |
| Schoenberg R, von Blanckenburg F. 2005. An assessment of the accuracy of stable Fe isotope ratio measurements on samples with organic and inorganic matrices by high-resolution multicollector ICP-MS. International Journal of Mass Spectrometry, 242(2-3): 257-272 |
| Siebert C, Nägler T F, Kramers J D. 2001. Determination of molybdenum isotope fractionation by double-spike multicollector inductively coupled plasma mass spectrometry. Geochemistry, Geophysics, Geosystems,2(7):1032 |
| White W M, Albarède F, Telouk P. 2000. High-precision analysis of Pb isotope ratios by multi-collector ICP-MS. Chemical Geology, 167(3-4): 257-270 |
| Woodhead J D, Hergt J M. 1997. Application of the 'double spike' technique to Pb-isotope geochronology. Chemical Geology, 138(3-4): 311-321 |
| Yang L. 2009. Accurate and precise determination of isotopic ratios by MC-ICP-MS: A review. Mass Spectrometry Reviews, 28(6): 990-1011 |
| Zhu J M, Johnson T M, Clark S K, Zhu X K. 2008. High precision measurement of selenium isotopic composition by hydride generation multiple collector inductively coupled plasma mass spectrometry with a 74Se-77Se double spike. Chinese Journal of Analytical Chemistry, 36(10): 1385-1390 |
| Zhu X K, O'Nions R K, Guo Y, Belshaw N S, Rickard D. 2000. Determination of natural Cu-isotope variation by plasma-source mass spectrometry: Implications for use as geochemical tracers. Chemical Geology, 163(1-4): 139-149 |
| Zhu X K, Guo Y, Williams R J P, O'Nions R K, Matthews A, Belshaw N S, Canters G W, de Waal E C, Weser U, Burgess B K, Salvato B. 2002. Mass fractionation processes of transition metal isotopes. Earth and Planetary Science Letters, 200(1-2): 47-62 |
| Zink S, Schoenberg R, Staubwasser M. 2010. Isotopic fractionation and reaction kinetics between Cr(Ⅲ)and Cr(Ⅵ)in aqueous media. Geochimica et Cosmochimica Acta, 74(20): 5729-5745 |
| 常向阳. 1999. 铅同位素研究新进展-"双稀释剂"测定方法和"AGSO-CSIRO"模式年龄. 地质地球化学, 27(2): 93-98 |
| 李津, 朱祥坤, 唐索寒. 2011a. 双稀释剂法在非传统稳定同位素测定中的应用-以钼同位素为例. 岩矿测试, 30(2): 138-143 |
| 李津, 朱祥坤, 唐索寒. 2011b. 钼同位素比值的双稀释剂测定方法研究. 地球学报, 32(5): 601-609 |
| 李理, 马腾, 刘存富, 蔡鹤生, 高永娟. 2009. 双稀释剂法铬同位素分析技术. 矿物岩石地球化学通报, 28(S): 74 |
| 王林森, 张利. 2003. 用双稀释法测定地质样品中的铅同位素组成. 矿物岩石, 23(2): 44-48 |
 2016, Vol. 35
2016, Vol. 35


