2. 华北水利水电大学 土木与交通学院 河南 郑州 450045;
3. 郑州大学 水利与环境学院 河南 郑州 450001
2. School of Civil Engineering and Transportation, North China University of Water Resources and Electric Power, Zhengzhou 450045, China;
3. School of Water Conservancy and Environment, Zhengzhou University, Zhengzhou 450001, China
冲击(爆炸)破岩涉及岩体中应力波的传播、岩体的损伤演化、岩体的破裂解体等多个过程, 加载应变率及能耗密度将直接影响岩体的动态力学特性及破碎特性.霍普金森杆(SHPB)实验是研究岩石动态力学特性及破碎特性的有效手段, 国内外的专家、学者利用SHPB对岩石的动态力学特性进行了大量的研究.文献[1]利用SHPB对磁铁矿的本构关系进行了研究, 测得了磁铁矿在不同应变率下的应力-应变关系.文献[2]通过动态单轴拉伸试验和巴西劈裂试验的对比, 得出岩石抗拉强度及弹性模量均随应变率的增加而增大, 但弹性模量的增幅较小.文献[3]研究表明, 磁铁矿、绿泥岩和混合岩的抗压强度、弹性模量均随应变率的增加而增大, 绿泥岩和混合岩的增幅大于磁铁矿.文献[4]研究表明, 试件破碎能耗密度与入射能量呈线性正比关系, 与试件平均应变率呈幂函数关系; 破碎能耗密度越大, 试件破碎程度越剧烈, 试件吸收能量主要耗散于岩石的损伤演化与变形破坏.文献[5]得出磁铁石英岩破碎能耗随平均应变率的增加而增大, 破碎能耗密度和入射能量呈多项式关系, 破碎后平均尺寸与能耗密度呈幂函数关系, 能耗密度越大, 岩石破碎程度越高.文献[6]以若干硬岩试件在不同应变率加载条件下的试验数据为基础, 分析了岩石动态抗压强度与静态抗压强度之比值与应变率的相关性, 结果表明, 岩石强度与应变率表现出较强或显著相关的特性.文献[7-8]对岩石在不同动、静组合加载下的力学特性进行了分析, 结果表明, 岩石的组合加载强度大于其纯静载强度或纯动载强度, 随着冲击动载的增加, 岩石组合加载强度增大.文献[9]开展了单裂纹圆孔板砂岩试样的冲击压缩实验, 分别采用实验-数值法和准静态法确定了砂岩试样动态断裂韧度.总体而言, 研究者们利用SHPB实验证明了岩石动态强度与应变率的相关性, 即随着应变率的增加, 岩石的动态强度将逐渐增大; 此外, 证明了随着加载应变率的增加, 用于试样破碎的能耗也逐渐增大, 从而在表观上呈现出随着应变率的增加, 试样破碎程度逐渐增高的现象.
然而, 岩石应变率的本质是什么, 是材料的本质属性, 或仅仅是材料的宏观响应?国内外的专家、学者并未对该问题进行深入研究.数值计算方法能够再现结构受力及断裂破坏的全过程[10-11].本文以SHPB实验的基本原理[12]为基础, 利用连续-非连续单元方法(CDEM)对赤铁矿试样的动态力学特性进行数值模拟研究, 试图从数值模拟的角度揭示岩石应变率效应的本质, 并分析能耗密度对岩石破碎程度的影响规律.
1 数值计算方法及岩体本构采用CDEM研究铁矿石数值试样在不同应变率下的动力响应及破坏模式.CDEM是一种有限元与离散元耦合的显式数值分析方法.数值模型由块体及界面两部分构成.块体由一个或多个有限元单元组成, 用于表征材料的弹性、塑性、损伤等连续特征; 两个块体间的公共边界即为界面, 用于表征材料的断裂、滑移、碰撞等非连续特征.CDEM中的界面包含真实界面及虚拟界面两个概念.真实界面用于表征材料的交界面、断层、节理等真实的不连续面, 其强度参数与真实界面的参数一致.虚拟界面主要有两个作用:一是连接两个块体, 用于传递力学信息; 二是为显式裂纹的扩展提供潜在的通道(即裂纹可沿着任意一个虚拟界面进行扩展).因此, 虚拟界面的强度参数与块体的强度参数一致.
采用的岩体本构为弹性-损伤-断裂本构, 其中在每个有限元单元上施加线弹性本构, 输入的参数包括密度、弹性模量及泊松比; 在虚拟界面上施加损伤-断裂本构, 输入的参数包括法向连接刚度、切向连接刚度、黏聚力、内摩擦角、抗拉强度、拉伸断裂能及剪切断裂能.
利用增量法表述的单元线弹性本构为
| $ \left\{ \begin{array}{l} \Delta {\sigma _{ij}} = 2G\Delta {\varepsilon _{ij}} + \left( {K - \frac{2}{3}G} \right)\Delta \theta {\delta _{ij}}, \\ {\sigma _{ij}}({t_1}) = \Delta {\sigma _{ij}} + {\sigma _{ij}}({t_0}), \end{array} \right. $ | (1) |
式中:σij为应力张量; Δσij为增量应力张量; Δεij为增量应变张量; Δθ为增量体应变; K为体积模量; G为剪切模量; δij为Kronecker记号; t0表示当前时步; t1表示下一时步.
虚拟界面上采用考虑强度线性软化效应的最大拉应力模型及Mohr-Coulomb模型进行损伤断裂的计算.首先采用增量法计算虚拟界面下一时步的法向及切向试探接触力, 可以表示为
| $ \left\{ \begin{array}{l} {F_{\rm{n}}}({t_1}) = {F_{\rm{n}}}({t_0}) - {k_{\rm{n}}} \times {A_{\rm{c}}} \times \Delta d{u_{\rm{n}}}, \\ {F_{\rm{s}}}({t_1}) = {F_{\rm{s}}}({t_0}) - {k_{\rm{s}}} \times {A_{\rm{c}}} \times \Delta d{u_{\rm{s}}}, \end{array} \right. $ | (2) |
式中:Fn、Fs为法向、切向接触力; kn、ks为单位面积上法向、切向接触刚度; Ac为虚拟界面的面积; Δdun、Δdus为法向、切向相对位移增量.
拉伸破坏的判断、法向接触力及抗拉强度的修正可以表示为:
| $ \begin{array}{l} \;\;\;\;\;\;{\rm{IF}}\;\;\; - {F_{\rm{n}}}({t_1}) \ge {\sigma _t}({t_0}){A_{\rm{c}}}, \\ {\rm{THEN}}\;\;\;{F_{\rm{n}}}({t_1}) = - {\sigma _t}({t_0}){A_{\rm{c}}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;{\sigma _t}({t_1}) = - {({\sigma _{t0}})^2} \times \Delta {u_{\rm{n}}}/(2{G_{{\rm{ft}}}}) + {\sigma _{t0}}, \end{array} $ | (3) |
式中:σt0、σ(t0)及σ(t1)为初始时刻、当前时刻及下一时刻虚拟界面上的抗拉强度; Δun为当前时刻虚拟界面上的法向相对位移; Gft为拉伸断裂能.
剪切破坏的判断、切向接触力及黏聚力的修正可以表示为:
| $ \begin{array}{l} \;\;\;\;\;\;{\rm{IF}}\;\;\;{F_{\rm{s}}}({t_1}) \ge {F_{\rm{n}}}({t_1}) \times \tan \phi + c({t_0}){A_{\rm{c}}}, \\ {\rm{THEN}}\;\;\;{F_{\rm{s}}}({t_1}) = {F_{\rm{n}}}({t_1}) \times \tan \phi + c({t_0}){A_{\rm{c}}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;c({t_1}) = - {({c_0})^2} \times \Delta {u_{\rm{s}}}/(2{G_{{\rm{fs}}}}) + {c_0}, \end{array} $ | (4) |
式中:ϕ为虚拟界面的内摩擦角; c0、c(t0)及c(t1)为初始时刻、当前时刻及下一时刻虚拟界面上的黏聚力; Δus为当前时刻虚拟界面上的切向相对位移; Gfs为剪切断裂能.
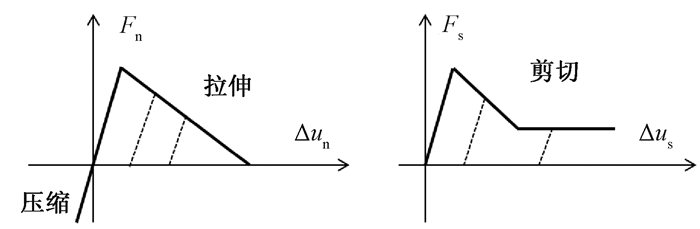
基于式(3)及式(4), 可绘制出虚拟界面上法向及切向的本构曲线, 具体如图 1所示.
|
图 1 虚拟界面上的本构曲线 Fig. 1 Constitutive curves in virtual interface |
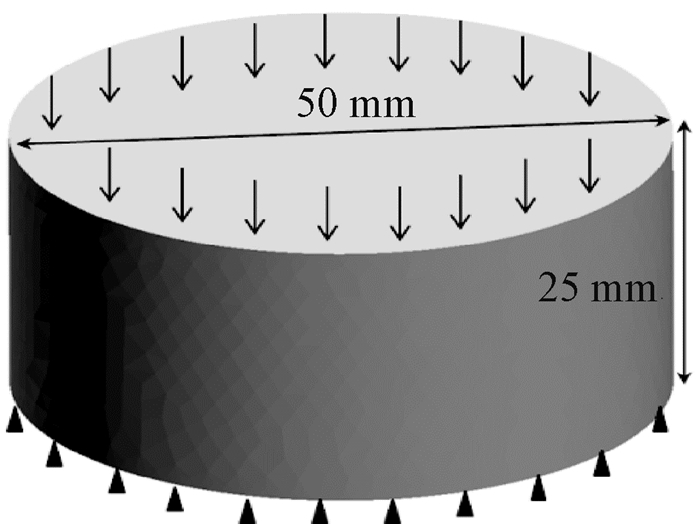
建立直径为50 mm、厚度为25 mm的赤铁矿数值试样模型, 如图 2所示, 并采用63 900个四面体单元对该模型进行剖分.
|
图 2 数值试样模型 Fig. 2 Numerical model |
数值模型执行连续-非连续计算时, 弹性单元本构参数中, 密度为3 300 kg/m3, 弹性模量为60 GPa, 泊松比为0.25;虚拟界面本构参数中, 法向、切向刚度为1016 Pa/m, 黏聚力为36 MPa, 内摩擦角为40°, 抗拉强度为12 MPa, 剪切断裂能为2 000 Pa·m, 拉伸断裂能为200 Pa·m.
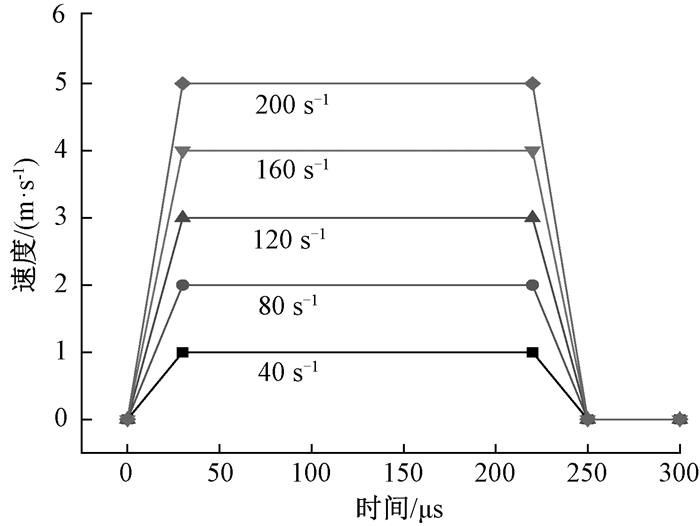
模型的底部为法向约束, 模型顶部施加竖直向下的脉冲式载荷, 参考SHPB的加载曲线, 各应变率下的加载持续时间均为250 μs, 其中上升段及下降段的持续时间为30 μs, 平台段的持续时间为190 μs, 探讨了5种加载应变率的影响, 脉冲式加载时程曲线如图 3所示.
|
图 3 不同应变率下的脉冲式加载时程曲线 Fig. 3 Time-history curves of impulse load at different strain rates |
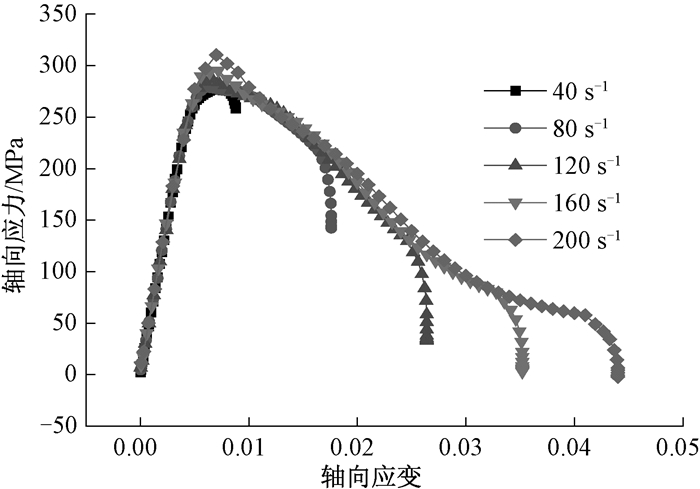
在不同应变率的加载作用下, 对单元顶部的平均应力进行监测, 不同应变率下的应力-应变曲线如图 4所示.由图 4可得, 在线弹性阶段, 随着应变率的增大, 应力-应变的关系基本一致; 在非线性上升段及软化段, 应变率越大, 试样的峰值强度越高, 峰后的下降段越长.
|
图 4 不同应变率下的应力-应变曲线 Fig. 4 Stress-strain curves at different strain rates |
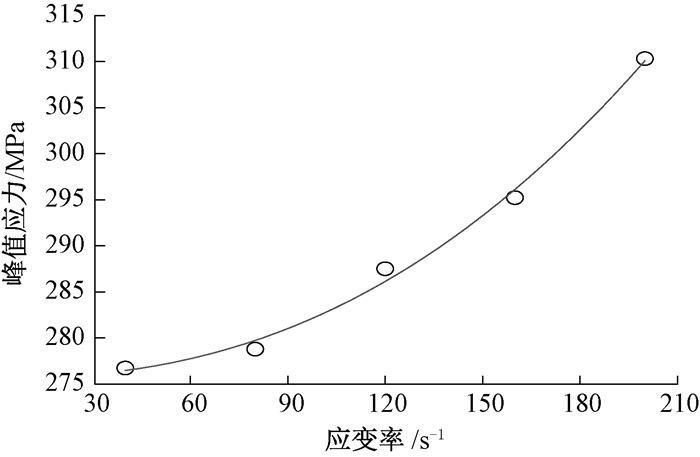
对图 4中的峰值强度进行统计, 绘制峰值强度与应变率的关系曲线, 结果如图 5所示.由图 5可得, 应变率从40 s-1增加至200 s-1, 峰值强度按幂函数形式从277 MPa增大至310 MPa(幂指数为2.33).
|
图 5 峰值强度与应变率的关系曲线 Fig. 5 The relationship curve between peak strength and strain rate |
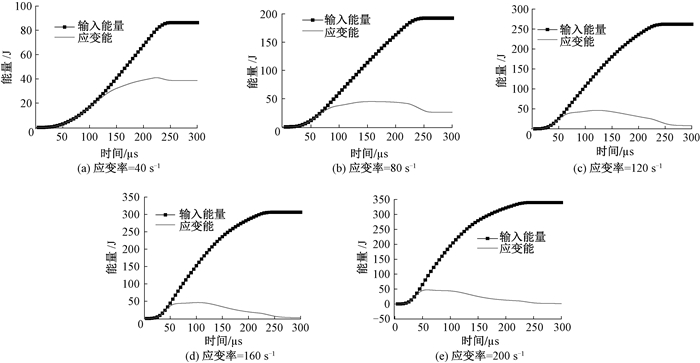
不同应变率下的输入能量及应变能时程曲线如图 6所示.可以看出, 随着加载时间的增加, 外界输入能量先缓慢增大, 而后匀速增大, 最后保持不变; 而系统应变能则呈现出先缓慢增加至峰值, 而后缓慢下降的过程.此外, 随着应变率的增大, 输入能量由86 J增加至340 J, 而系统应变能的峰值基本为40~50 J.
|
图 6 不同应变率下的输入能量及应变能时程曲线 Fig. 6 Time-history curves of input energy and strain energy at different strain rates |
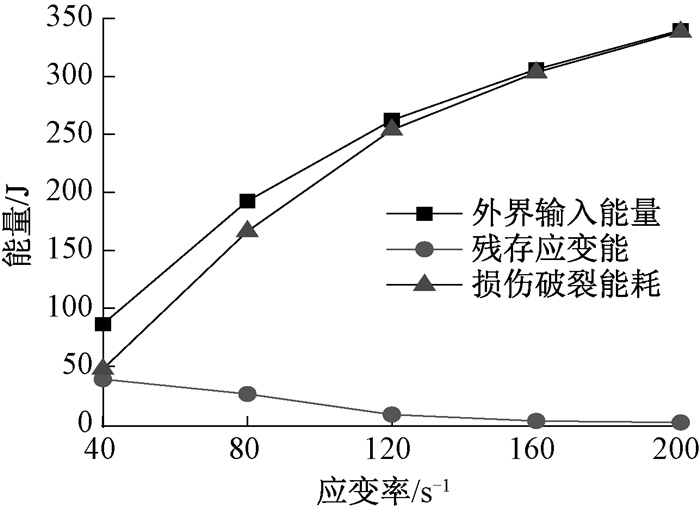
300 μs加载结束后, 外界输入能量、残存应变能及损伤破裂能耗与应变率的关系如图 7所示.其中, 损伤破裂能耗可由输入能量与残存应变能的差值获得.可以看出, 随着应变率的增加, 外界输入能量及损伤破裂能耗均逐渐增大, 而系统残存应变能则逐渐减小.此外, 外界输入能量绝大部分用于试样的损伤破裂, 且应变率越高, 用于损伤破裂的能耗占比越大.
|
图 7 能耗与应变率的关系曲线 Fig. 7 The relationship curves between energy consumption and strain rate |
不同应变率下的试样破裂状态如图 8所示.可以看出, 在脉冲式加载的情况下, 随着应变率的增加, 试样的破裂程度逐渐增大.应变率为40 s-1时, 试样未发生破裂, 应变率为200 s-1时, 试样已经发生了解体破坏.

|
图 8 不同应变率下的试样破裂状态 Fig. 8 Fracture pattern of specimens at different strain rates |
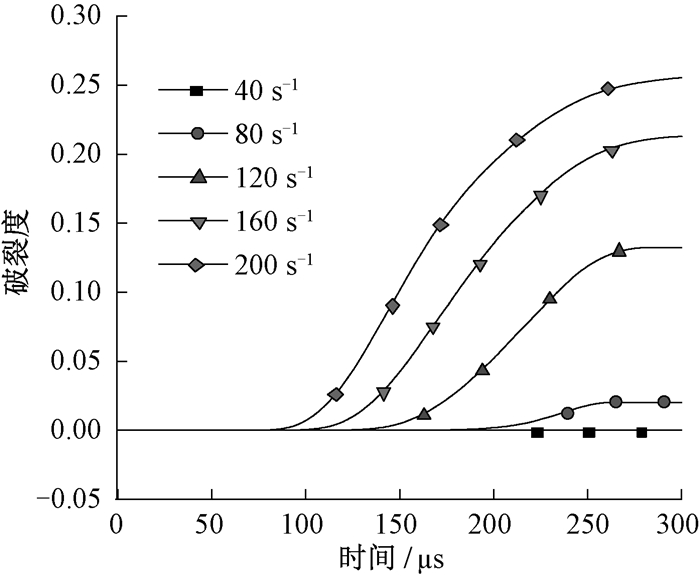
定义破裂度为模型已经破裂的虚拟界面面积与模型总虚拟界面面积的比值, 则不同应变率下的破裂度时程曲线如图 9所示.可以看出, 随着加载时间的增加, 系统破裂度逐渐增大; 当加载时间超过250 μs后, 系统破裂度基本保持不变.此外, 由图 9还可以看出, 应变率越大, 系统的破裂度越大.
|
图 9 不同应变率下的破裂度时程曲线 Fig. 9 Time-history curves of fracture degree at different strain rates |
定义能耗密度为损伤破裂能耗与试样体积的比值, 表示为
| $ {\rho _{\rm{w}}} = {E_{\rm{f}}}/V, $ | (5) |
式中:ρw为能耗密度; Ef为损伤破裂能耗; V为试样体积.
对图 9中的终态破裂度进行统计, 绘制破裂度与系统能耗密度的对应关系曲线, 对该曲线进行线性拟合, 可得破裂度与能耗密度的函数关系为
| $ {F_{\rm{d}}} = - 0.21 + 0.068{\rho _{\rm{w}}}, $ | (6) |
式中:Fd为系统破裂度.定义试样的特征破碎尺寸为试样体积与破裂总面积的比值, 可以表示为
| $ d = V/{A_{\rm{f}}}, $ | (7) |
式中:d为试样的特征破碎尺寸; Af为试样破裂的总面积.
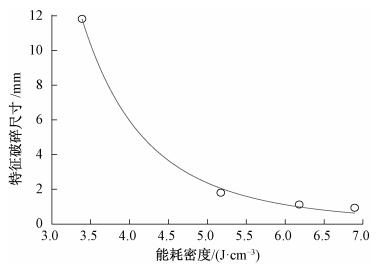
绘制试样特征破碎尺寸与系统能耗密度的关系曲线, 结果如图 10所示.可以看出, 能耗密度与试样破裂度及特征破碎尺寸密切相关, 当能耗密度增大至6.9 J/cm3时, 试样破裂度线性增大至25.5%, 特征破碎尺寸则按幂函数形式迅速减小至1 mm.
|
图 10 特征破碎尺寸与系统能耗密度的关系曲线 Fig. 10 The relationship curve between characteristic size of fragments and system energy consumption density |
基于连续-非连续的数值模拟方法, 以SHPB为模拟对象, 研究了铁矿石在不同应变率下的应力-应变关系、峰值强度及破裂特征的演化规律, 结果表明:在单元本构及虚拟界面本构中未引入应变率效应的情况下, 数值试样的动态单轴抗压强度表现出较强的应变率相关性; 随着加载应变率的增加, 试样的动态强度按幂函数形式增大, 数值试样中用于损伤破裂的能耗密度也增大; 能耗密度与试样破裂度及特征破碎尺寸密切相关, 随着能耗密度的增大, 特征破碎尺寸则按幂函数形式迅速减小.
| [1] |
单仁亮.岩石冲击破坏力学模型及其随机性研究[D].北京: 中国矿业大学, 1997. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y237371
(  0) 0) |
| [2] |
李海波, 王建伟, 李俊如, 等. 单轴压缩下软岩的动态力学特性试验研究[J]. 岩土力学, 2004, 25(1): 1-4. DOI:10.3969/j.issn.1000-7598.2004.01.001 (  0) 0) |
| [3] |
郑永强.大孤山铁矿岩石动态特性与爆破振动实验研究[D].鞍山: 辽宁科技大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10146-1014174537.htm
(  0) 0) |
| [4] |
平琦, 骆轩, 马芹永, 等. 冲击载荷作用下砂岩试件破碎能耗特征[J]. 岩石力学与工程学报, 2015, 34(S2): 4197-4203. (  0) 0) |
| [5] |
郭连军, 杨跃辉, 张大宁, 等. 冲击荷载作用下磁铁石英岩破碎能耗分析[J]. 金属矿山, 2014, 43(8): 1-5. (  0) 0) |
| [6] |
梁昌玉, 李晓, 李守定, 等. 岩石静态和准动态加载应变率的界限值研究[J]. 岩石力学与工程学报, 2012, 31(6): 1156-1161. DOI:10.3969/j.issn.1000-6915.2012.06.009 (  0) 0) |
| [7] |
李夕兵, 周子龙, 叶州元, 等. 岩石动静组合加载力学特性研究[J]. 岩石力学与工程学报, 2008, 27(7): 1387-1395. DOI:10.3321/j.issn:1000-6915.2008.07.011 (  0) 0) |
| [8] |
王其胜, 李夕兵. 动静组合加载作用下花岗岩破碎的分形特征[J]. 实验力学, 2009, 24(6): 587-591. (  0) 0) |
| [9] |
倪敏, 苟小平, 王启智. 霍普金森杆冲击压缩单裂纹圆孔板的岩石动态断裂韧度试验方法[J]. 工程力学, 2013, 30(1): 365-372. (  0) 0) |
| [10] |
杜云海, 刘雯雯, 徐轶洋. 对接双材平面中圆弧裂纹问题的数值方法[J]. 郑州大学学报(理学版), 2014, 46(1): 98-102. DOI:10.3969/j.issn.1671-6841.2014.01.022 (  0) 0) |
| [11] |
于洋, 邬亚滨, 张云峰, 等. 混凝土强度对GFRP管-混凝土-钢管组合柱性能的影响[J]. 郑州大学学报(理学版), 2016, 48(3): 118-123. (  0) 0) |
| [12] |
陈强, 王志亮. 分离式霍普金森压杆在岩石力学实验中的应用[J]. 实验室研究与探索, 2012, 31(11): 146-149. DOI:10.3969/j.issn.1006-7167.2012.11.043 (  0) 0) |
 2019, Vol. 51
2019, Vol. 51

