2. 西南大学 数学与统计学院 重庆 400715
2. School of Mathematics and Statistics, Southwest University, Chongqing 400715, China
粗糙集理论是由波兰数学家Pawlak[1]提出的,它是一种用来处理不精确、不完全数据问题的一种理论,其研究的主要内容之一是属性约简(知识约简)[2-6].所谓属性约简,就是在保持知识库的数据分类能力不变的条件下,删除其中不相关或不重要的属性,从而达到减少冗余数据和简化规则的目的,实现了知识的简化.在Pawlak粗糙集的背景之下, 不同的学者根据不同的约简思想, 已经给出了不同的属性约简算法[7].文献[8]提出了基于差别矩阵的属性约简算法, 因差别矩阵的直观简明性而受到了广大学者的关注.文献[9]给出了基于差别矩阵的Rough集属性约简算法以及属性约简的完备算法.文献[10]也给出了一种基于差别矩阵的属性约简完备算法.不仅如此,根据差别矩阵的不同定义,人们也提出了很多有效的关于属性约简的启发式算法,但是这些算法要想得到约简就必须用到差别矩阵中所有的非空元素.文献[8]指出,每一个信息系统对应的差别矩阵中所有非空元素的合取构成了该信息系统的属性约简集,由合取运算可知,差别矩阵的重复元素和父集元素在求取属性约简时起不到任何作用,但这些元素却占用了大量的存储空间,同时也增加了求取约简的时间.为了消除差别矩阵中重复元素的出现,文献[11]提出了一种新的差别矩阵存储方法,实现了差别矩阵的压缩储存.为了消除差别矩阵中冗余的父集元素,文献[12]给出了一种基于差别信息树的属性约简算法, 该算法不仅能消除差别矩阵中的重复元素, 而且在大多数情况下亦能消除父集元素的影响, 实现对差别矩阵的压缩储存.
由于差别信息树是在等价关系下差别矩阵的基础上提出的,而等价关系下的差别矩阵是一个对称矩阵.因此,在求信息系统的约简时可以只用差别矩阵中的上三角元素或者只用下三角元素.当研究序信息系统时,因为由序信息系统得到的差别矩阵具有非对称性,所以基于差别信息树的属性约简并不一定适用于不协调序决策信息系统下的属性约简.本文在差别信息树的基础上提出了基于分配可辨识矩阵的差别信息树, 给出了适用于不协调序决策信息系统的分配约简算法.
1 预备知识定义1[13] 设一个决策信息系统为四元组I=(U, AT∪DT, F, G), 而三元组I=(U, AT, F)为信息系统, 其中:U={x1, x2, …, xn}是有限对象集;AT={a1, a2, …, ap}是有限条件属性集;DT={d1, d2, …, dq}是有限决策属性集, 且AT∩DT=∅;F={f|U→Va, a∈AT}是U与AT的关系集, Va为a的有限值域;G={g|U→Vd, d∈DT}是U与DT的关系集, Vd为d的有限值域.
定义2[13] 设I=(U, AT∪DT, F, G)为决策信息系统, 对于任意A⊆AT, D⊆DT, RA≥与RD≥称为决策信息系统I中条件属性集A与决策属性集D对应的优势关系, 该信息系统称为序决策信息系统, 记作I≥.
定义3[13] 设I≥=(U, AT∪{d}, F, G)为序决策信息系统,对于任意A⊆AT,记σA(x)={Dj Dj∩[x]A≥≠∅, x∈U},称σA(x)为论域U上对象x关于属性子集A和决策d的分配函数.
定义4[13] 设I≥=(U, AT∪{d}, F, G)为不协调序决策信息系统,A⊆AT.若对任意x∈U都有σA(x)= σAT(x),则称A是I≥中关于优势关系RAT≥的分配相对协调集,简称为分配协调集.进而,若A的任何真子集都不是分配协调集,则称A为I≥中关于优势关系RAT≥的分配约简,简称为分配约简.
定义5[13] 设I≥=(U, AT∪{d}, F, G)为不协调序决策信息系统, 记
| $\begin{array}{l} D_{ \ge AT}^\sigma = \{ ({x_i},{x_j}){\rm{|}}{\sigma _{AT}}({x_i}) \subset {\sigma _{AT}}({x_j})\} ,\\ Dis_{ \ge AT}^\sigma ({x_i},{x_j}) = \left\{ \begin{array}{l} \{ {a_k} \in AT{\rm{|}}f({x_i},a) > f({x_j},a)\} ,({x_i},{x_j}) \in D_{ \ge AT}^\sigma ,\\ \emptyset ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;({x_i},{x_j}) \notin D_{ \ge AT}^\sigma , \end{array} \right. \end{array}$ |
称Dis≥ATσ(xi, xj)为I≥中对象xi、xj关于优势关系RAT≥的分配相对可辨识属性集, 简称为分配可辨识属性集.记Dis≥ATσ=(Dis≥ATσ(xi, xj))|U|×|U|, 称Dis≥ATσ为I≥中对象关于优势关系RAT≥的分配相对可辨识矩阵, 简称为分配可辨识矩阵.
定义6[13] 设I≥=(U, AT∪{d}, F, G)为不协调序决策信息系统, I≥中对象关于优势关系RAT≥的分配可辨识矩阵为Dis≥ATσ.记M≥ATσ=∧{∨{a|a∈Dis≥ATσ(xi, xj)}∀xi, xj∈U}, 称M≥ATσ为I≥中对象关于优势关系RAT≥的分配可辨识公式.
分配可辨识公式的极小析取范式中的所有合取式是不协调序决策信息系统的分配约简.
例1 表 1为一个不协调序决策信息系统,表 2为表 1所对应的信息系统的分配可辨识矩阵.由表 2的分配可辨识矩阵可得:M≥Aσ=(a1∨a3)∧a3∧(a1∨a3)∧a3∧(a1∨a3)∧a3∧(a1∨a2∨a3)∧(a1∨a2)∧a3=(a1∨a3)∧a3∧(a1∨a2∨a3)∧(a1∨a2)=(a1∧a3)∨(a2∧a3).
|
|
表 1 一个不协调序决策信息系统 Tab. 1 An uncoordinated ordinal decision information system |
|
|
表 2 分配可辨识矩阵 Tab. 2 Assignment identifiable matrix |
所以表 1中不协调序决策信息系统的分配约简为{a1, a3}与{a2, a3}.
2 基于分配可辨识矩阵的差别信息树的设计与实现定义7[12] 差别信息树是一棵有序树, 其中序体现在它的条件属性的顺序是一个从左到右的序列, 其顺序不能更改或颠倒.
差别信息树的特征有以下几个方面:①差别信息树的每个节点最多有|AT|个孩子节点, 其中|AT|为带决策的信息系统中条件属性的个数.②差别信息树的每个节点由前缀指针、后继指针、节点名、同名指针组合而成.其中前缀指针指向该节点的前缀节点(即父亲节点),后继指针指向该节点的后继节点(即孩子节点),节点名标记了该节点所对应的条件属性名,同名指针指向该差别信息树中与该节点具有相同节点名的其他路径中的节点.③差别信息树的子树同样是一棵有序树,其中条件属性的顺序同样不能更改或颠倒.
算法1 序决策信息系统中基于分配可辨识矩阵的差别信息树的构建算法.
输入:一个不协调序决策信息系统I≥=(U, AT∪{d}, F, G);
输出:该序决策信息系统所对应的差别信息树.
getDI-tree(decision table I≥)
{
(1)创建差别信息树的根节点TN,并令TN为null;
(2)根据定义5中的公式求出所有对象对(xi, xj)的分配可辨识属性集Dis≥ATσ(xi, xj),将其构成一个分配可辨识矩阵Dis≥ATσ=(Dis≥ATσ(xi, xj))|U|×|U|, 设B⊂AT为任意一个对象对的分配可辨识属性集,且集合B中元素按信息系统中条件属性从左到右的顺序排列.
While(B≠∅)
{
A.选择B中最左边的元素为a;
B. if(TN所有子节点中存在属性名为a的子节点N)
{
如果N是一叶子节点,则采用不扩展路径策略,不构建B中剩余属性对应的节点;
如果a为B中最后一个元素,则采取删除子树策略,从差别信息树中删除以节点N为根的子树, 但保留节点N;
否则令TN=N;
}
else
{
a)创建一新节点N′,节点N′作为TN一子节点,同时初始N′的属性名为a,并通过该节点的同名指针连接到与该节点具有相同属性名的节点上,从而构成了一个同名属性节点链;
b)令TN=N′;
}
C.令B⇐B-{a};
}
}
例2 根据算法1及表 2给出该序决策信息系统中基于分配可辨识矩阵的差别信息树的构建过程:
1) 创建序决策信息系统基于分配可辨识矩阵的差别信息树的根节点.根据分配可辨识矩阵中的每一个条件属性子集,将子集中的属性次序按序决策信息系统中条件属性从左到右的顺序排列.
2) 构建分配可辨识矩阵中第一个属性子集{a1, a3}所对应的路径〈a1, a3〉, 将该路径插入到要构建的差别信息树中.
3) 根据可辨识矩阵中第二个属性子集{a3}创建另一条新的路径〈a3〉.
4) 对于第三个与第五个属性子集{a1, a3},因为它们与第一个属性子集完全相同,所以第三个与第五个属性子集{a1, a3}所对应的路径也映射到〈a1, a3〉上.
5) 同4),将第四个、第六个与第九个属性子集{a3}所对应的路径映射到〈a3〉上.
6) 对于第七个属性子集A={a1, a2, a3},创建另一条新的路径〈a1, a2, a3〉,它与属性{a1, a3}共享前缀〈a1〉.
7) 对于第八个属性子集{a1, a2},因为{a1, a2}⊂A,采用删除子树策略,从路径〈a1, a2, a3〉中删除a2之后的所有节点,即路径〈a1, a2, a3〉被修改为〈a1, a2〉.
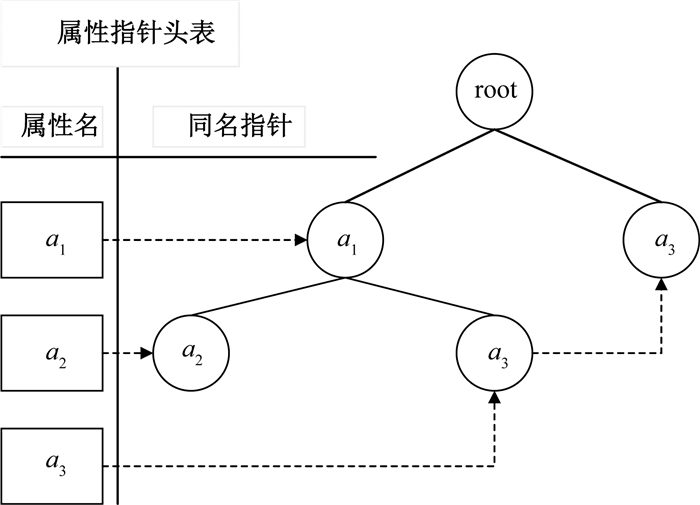
图 1给出了所构建的基于分配可辨识矩阵的差别信息树.在构建过程中采用不扩展路径策略以及删除子树策略,将相同的分配可辨识属性集映射到同一条路径中.将具有相同前缀的分配可辨识属性集{a1, a2}与{a1, a2, a3}映射到同一条路径〈a1, a2〉中.分配可辨识矩阵中属性集{a1, a2, a3}与{a1, a3}共享前缀〈a1〉, 达到对分配可辨识矩阵的压缩储存,从而减少了构建基于分配可辨识矩阵的差别信息树的时空复杂度.
|
图 1 基于分配可辨识矩阵的差别信息树 Fig. 1 Discernibility information tree based on assignment identifiable matrix |
定理1 基于分配可辨识矩阵的差别信息树中包括了能够获得不协调序决策信息系统的分配约简所需要的所有属性.
证明 设集合DS包含了基于分配可辨识矩阵的差别信息树中所有路径的分配可辨识属性集, 集合Dis≥ATσ为分配可辨识矩阵.由基于分配可辨识矩阵的差别信息树的构建过程可知:DS⊆Dis≥ATσ, 对于任意一个Dis≥ATσ(xi, xj)∈Dis≥ATσ, 存在Dis≥ATσ(x′ i, x′ j)∈DS, 使得Dis≥ATσ(x′ i, x′ j)⊆Dis≥ATσ(xi, xj).由分配可辨识公式可知:Dis≥ATσ(xi, xj)与Dis≥ATσ(x′ i, x′ j)进行合取运算的结果还是Dis≥ATσ(x′ i, x′ j).综上所述, 基于分配可辨识矩阵的差别信息树中包括了能够获得不协调序决策信息系统的分配约简所需要的所有属性.
定理2 基于分配可辨识矩阵的差别信息树中,所有只有一个节点的路径所对应的分配可辨识属性集,构成了该序决策信息系统中条件属性集的核cored(A).
证明 由基于分配可辨识矩阵的差别信息树的构建过程可知:假设该信息树中某一节点的属性名为a, 并且该树中存在某一条路径仅包含属性名为a的节点, 则存在分配可辨识属性集{a}与该路径对应.在分配可辨识矩阵中, 若a∈A且{a}为分配可辨识矩阵中的一个非空元素, 则称a相对d在A中是必要的.A的所有必要属性的集合构成了A相对d的核, 即cored(A).
定理3 设R是基于分配可辨识矩阵的差别信息树中根节点的所有子节点所代表的条件属性集合, 则σR(x)=σA(x)成立.
证明 由定理1, 并设集合DS包含了基于分配可辨识矩阵的差别信息树中所有路径的分配可辨识属性集, 对于任意的Dis≥ATσ(xi, xj)∈DS, 有R∩Dis≥ATσ(x′ i, x′ j)≠∅, 从而进一步证明了σR(x)=σA(x)成立.
基于定理3, 只要删除R中所有不必要的条件属性, 就可以得到该序决策信息系统的一个完备约简.
给定一个不协调的带决策的序信息系统I≥=(U, A∪{d}, F, G), 如果该序信息系统中有|U|个对象以及|A|个条件属性, 则在分配可辨识矩阵中最多可以得到|U|2个非空的条件属性的子集(即差别信息).假设分配可辨识矩阵中实际的非空条件属性的子集数为M(一般情况下M < < |U|2),由例2的构建过程可以看出,一棵差别信息树最多可以有M条不同的路径, 并且每一条路径中最多可以有|A|个节点,所以一棵差别信息树中最多可以有M|A|个节点,又由于在基于分配可辨识矩阵的差别信息树中,许多路径都存在共享前缀,导致差别信息树中的实际节点数远小于M|A|.因此,在最坏的情况下,基于分配可辨识矩阵的差别信息树的空间复杂度为O(|A|*|U|2).
另外,在构建基于分配可辨识矩阵的差别信息树的过程中,向差别信息树中插入路径的次数最多为|U|2次,并且在构建路径的过程中最多比较并插入|A|个节点,删除Mi(其中i∈{1, 2, …, |U|2})个节点.因此,基于分配可辨识矩阵的差别信息树的时间复杂度为|A|*|U|2+(M1+M2+…+M|U|2).已知在一棵差别信息树中最多可以有|A|*|U|2个节点,则M1+M2+…+M|U|2的值至多为|A|*|U|2.综上所述,基于分配可辨识矩阵的差别信息树的时间复杂度也为O(|A|*|U|2).
3 基于分配可辨识矩阵的差别信息树的分配约简算法为了验证所提出的序决策信息系统中基于分配可辨识矩阵的差别信息树的有效性,算法2给出了基于该差别信息树的分配约简完备算法.
算法2 序决策信息系统中基于分配可辨识矩阵的差别信息树的分配约简算法.
输入:序决策信息系统中基于分配可辨识矩阵的差别信息树;
输出:不协调序决策信息系统的一个分配约简.
Step 1 创建一个空集R.
Step 2 获取基于分配可辨识矩阵的差别信息树中只有一个节点的路径,将这些节点对应属性名放在一个集合R′中.
Step 3 如果R′≠∅,则对于∀a∈R′,在由分配可辨识矩阵得到的差别信息树中删除包含属性a的所有路径.
Step 4 令R⇐R′.
Step 5 如果由分配可辨识矩阵得到的差别信息树中只含有根节点,则转Step 7.
Step 6 在由分配可辨识矩阵得到的差别信息树中, 选择根节点最右边的子节点, 假设该子节点为b, 令R⇐R∪{b}, 并从由分配可辨识矩阵得到的差别信息树中删除含有节点{b}的路径, 转Step 5.
Step 7 输出R,算法结束.
例3 基于图 1,算法2的求解过程如下:
1) 创建一个空集R.
2) 从基于分配可辨识矩阵的差别信息树中获取只含有一个节点的路径〈a3〉,令R⇐{a3},然后删除信息树中含有属性名为a3的全部路径.
3) 此时基于分配可辨识矩阵的差别信息树中仅含有一条路径〈a1, a2〉,选取根节点最右边的子节点a1,令R⇐R∪{a1},然后删除信息树中含有属性名为a1的全部路径.
4) 此时图 1给出的基于分配可辨识矩阵的差别信息树只剩下根节点,输出R⇐{a3, a1},算法结束.因而{a3, a1}即为通过基于分配可辨识矩阵的差别信息树所求得的一个约简.
下面给出算法2的完备性证明.根据分配约简的定义, 从分配可辨识矩阵的角度出发, 若R⊆A是给定的不协调序信息系统的完备分配约简, 则R应满足两个条件:①对于任意的B∈Dis≥ATσ, B∩R≠∅; ②对于任意的a∈R, 存在B∈Dis≥ATσ, 使得B∩(R-{a})=∅.根据定理1, 并设集合DS包含了基于分配可辨识矩阵的差别信息树中所有路径对应的分配可辨识属性集, 则从基于分配可辨识矩阵的差别信息树的角度考虑, 以上两个条件等价于:①对于任意的B∈DS,B∩R≠∅;②对于任意的a∈R, 存在B∈DS, 使得B∩(R-{a})=∅.如果要证明算法2是完备的,只需要证明算法2所输出的R满足以上两个条件即可.根据算法2可知,对于任意的B∈DS,B∩R≠∅成立.将算法2中得到的决策表的核cored(A)作为分配约简的一部分, 然后从由分配可辨识矩阵得到的差别信息树中删除包含cored(A)中元素的所有路径.令R′⇐R-cored(A),假设r是R′中最右边的一个元素, 则在当前的差别信息树中, 根节点最右边的一个子节点所对应的属性一定是r, 并且以该节点为根的子树中一定不包含R′-{r}中任意属性所对应的节点, 从而可知r∈R, 存在B∈DS, 使得B∩(R-{r})=∅.同理可证, R′中除r以外的其他元素也满足该条件.综上所述, 算法2得到的分配约简是完备约简.
4 结论在差别信息树的基础上提出了一种能压缩储存分配可辨识矩阵的数据结构,即基于分配可辨识矩阵的差别信息树.和直接通过分配可辨识公式的极小析取范式求分配约简相比,通过该差别信息树可以大大缩短求取不协调序信息系统的分配约简的时空复杂度.但是从基于分配可辨识矩阵的构建过程可知,将分配可辨识属性集插入到差别信息树中用到的条件属性的顺序是决策表中属性的原始顺序,没有考虑属性重要度以及核属性对基于分配可辨识矩阵的差别信息树在构建过程中的影响,并且通过该差别信息树只能得到决策表的一个约简.下一步的工作是结合属性重要度以及核属性来完善该差别信息树的构建,看能否实现对分配可辨识矩阵的进一步压缩储存.
| [1] |
PAWLAK Z. Rough sets[J]. Internationtal journal of computer and information sciences, 1982, 11(5): 341-356. (  0) 0) |
| [2] |
张小红, 裴道武, 代建华. 模糊数学与Rough集理论[M]. 北京: 清华大学出版社, 2013.
(  0) 0) |
| [3] |
徐伟华, 张文修. 基于优势关系下不协调目标信息系统的分布约简[J]. 模糊系统与数学, 2007, 21(4): 124-131. DOI:10.3969/j.issn.1001-7402.2007.04.023 (  0) 0) |
| [4] |
米据生, 吴伟志, 张文修. 不协调目标信息系统知识约简的比较研究[J]. 模糊系统与数学, 2003, 17(3): 54-60. DOI:10.3969/j.issn.1001-7402.2003.03.008 (  0) 0) |
| [5] |
张文修, 米据生, 吴伟志. 不协调目标信息系统的知识约简[J]. 计算机学报, 2003, 26(1): 12-18. DOI:10.3321/j.issn:0254-4164.2003.01.002 (  0) 0) |
| [6] |
徐伟华, 张文修. 基于优势关系下不协调目标信息系统的知识约简[J]. 计算机科学, 2006, 33(2): 182-184. DOI:10.3969/j.issn.1002-137X.2006.02.051 (  0) 0) |
| [7] |
THANGAVEL K, PETHALAKSHMI A. Dimensionality reduction based on rough set theory:a review[J]. Applied soft computing, 2009, 9(1): 1-12. (  0) 0) |
| [8] |
SKOWRON A, RAUSZER C. The discernibility matrices and functions in information systems[M]//Intelligent Decision Support, Handbook of Applications and Advances of the Rough Sets Theory. Dordrecht: Kluwer Academic Publishers, 1991: 331-362.
(  0) 0) |
| [9] |
蒋瑜, 王燮, 叶振. 基于差别矩阵的Rough集属性约简算法[J]. 系统仿真学报, 2008, 20(14): 3717-3720. (  0) 0) |
| [10] |
王兵, 陈善本. 一种基于差别矩阵的属性约简完备算法[J]. 上海交通大学学报, 2004, 38(1): 43-46. (  0) 0) |
| [11] |
YANG M, YANG P. A novel condensing tree structure for rough set feature selection[J]. Neurocomputing, 2008, 71(4): 1092-1100. (  0) 0) |
| [12] |
蒋瑜. 基于差别信息树的rough set属性约简算法[J]. 控制与决策, 2015, 30(8): 1531-1536. (  0) 0) |
| [13] |
徐伟华. 序信息系统与粗糙集[M]. 北京: 科学出版社, 2013.
(  0) 0) |
 2019, Vol. 51
2019, Vol. 51


