2. 山西大学 计算机与信息技术学院 山西 太原 030006
2. School of Computer and Information Technology, Shanxi University, Taiyuan 030006, China
在多属性群决策问题中,由于决策评价者自身犹豫或知识缺乏,其评价中往往存在着肯定、否定以及犹豫3个方面,针对这一现象,一些学者提出了直觉模糊集以及区间直觉模糊集,用以求解此类决策问题[1-3].文献[4]借鉴理想点的求解思路提出了区间直觉模糊数表达的多属性群决策问题的相关系数求解方案,其集结权重运用熵法求得.文献[5]分析了经典区间直觉模糊集结算子,并给出了直觉模糊环境下的Hamacher集结算子,结合Hamacher算子的优势将其运用到多属性群决策问题中.文献[6]给出了区间直觉模糊表达下的连续最大熵权确定方法,结合经典集结算子求解多属性群决策问题.文献[7]给出了一种非犹豫得分函数,用以比较区间直觉模糊数的大小.这些方法采用不同技术确定区间或区间直觉模糊多属性群决策问题中的属性权重和专家权重指标,提供了问题求解的新方法与新思路.然而在实际决策中,除了要求专家给出标书的各个属性评价区间直觉模糊数外,还经常要求对决策对象进行初步的等级确定.这种初步评价信息反映了专家对评价的粗粒度偏好信息,在现实决策中具有重要的参考价值与决策意义.而现有的绝大多数多属性群决策的研究均基于决策矩阵,很少考虑此类问题.文献[8]首次将初步分级决策引入多属性群分级决策模型,设计了一种基于粒计算的多属性群决策模型,并计算出了具有解释意义的决策参数.现实生活中存在着大量的具有确定分级表达的区间直觉模糊多属性群决策问题,现有模型无法有效求解.
本文针对确定分级表达下的区间直觉模糊多属性群决策问题,提出一种基于粒计算的区间直觉模糊多属性群决策方法.最后给出人力资源管理实例说明所提方法的有效性与实用性.
1 基本概念 1.1 区间直觉模糊数定义1[2] 设X是一个非空集合, 则称
定义2 设
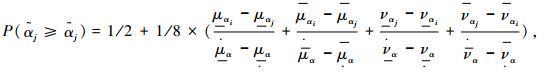
|
(1) |
其中: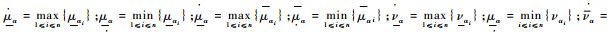
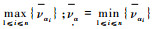
相对大于可能度考虑区间直觉模糊数集可能涉及范围,可以刻画不同程度的优势,是相对于当前判断而言的.同时,给定区间直觉模糊数集
性质1
证明 由定义2知大于可能度的计算项满足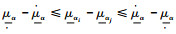
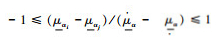
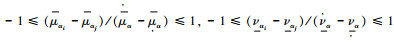
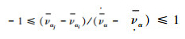
性质2
证明 从定义2计算易得.
性质3 若
证明 由
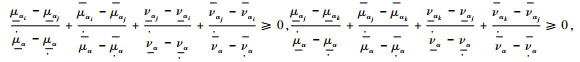
|
所以以上不等式左侧之和非负,故
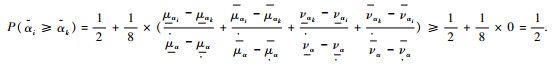
|
性质4
证明 采用添补项的方法得
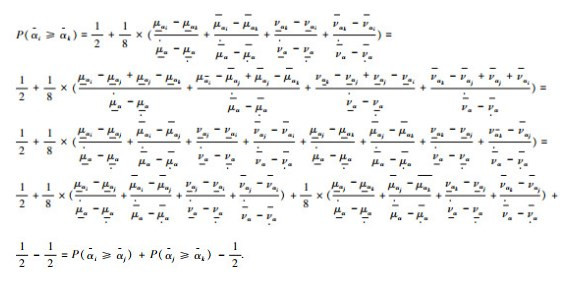
|
这4条性质表明新给出的相对大于可能度具有有界性、互补性,且满足max-max传递性及一致性.给定的区间直觉模糊数集
| $ {\lambda _i} = \frac{1}{n}\left( {\sum\limits_{j = 1}^n {P\left( {{{\tilde \alpha }_i},{{\tilde \alpha }_j}} \right)} + 1 - \frac{n}{2}} \right). $ | (2) |
设A={a1, a2, …, an}是n个对象,G={g1, g2, …, gs}是s个等级且满足,g1>g2>…>gs, f:A→G为从对象集到等级集合G的一个等级映射.每个映射可确定对象集上的一个优势粒结构为Rf={[ai]≥f|ai∈A}, 其中[ai]≥f={a|f(a)≥f(ai)}称为对象a在f下的优势粒结构.
不同的等级映射对应不同的粒结构,设f与f′是对象集A上的两个等级映射Rf和Rf′各自对应的优势粒结构.文献[9]定义一种优势粒结构相似度,可以精细描述等级映射的位置异同及差异.
定义3[9] 设Rf={[a1]≥f, [a2]≥f, …, [an]≥f},Rf′={[a1]≥f, [a2]≥f, …, [an]≥f}是集合A上的两个优势粒结构,Rf与Rf′之间的相似度为
| $ sim\left( {{R_f},{R_{f'}}} \right) = \left( {\sum\limits_{i = 1}^n {{{\log }_2}\frac{n}{{\left| {{{\left[ {{a_i}} \right]}^{ \ge f}} \cup {{\left[ {{a_i}} \right]}^{ \ge f'}}} \right|}}} } \right)/\left( {\sum\limits_{i = 1}^n {{{\log }_2}\frac{n}{{\left| {{{\left[ {{a_i}} \right]}^{ \ge f}} \cap {{\left[ {{a_i}} \right]}^{ \ge f'}}} \right|}}} } \right). $ | (3) |
若f与f′均为恒等映射,则规定sim(Rf, Rf′)=1.
定义3给定的相似度从取值范围、计算复杂性、位置敏感性方面均优于斯皮尔曼相关系数.可用来刻画数据取值序结构的敏感变化.
2 带确定分级偏好的区间直觉模糊多属性群决策模型描述设A={a1, a2, …, an}(n>1)为评价对象集,E={e1, e2, …, el}(l>1)为专家集,C={c1, c2, …, cm}(m>1)为评价属性集,d为初步分级决策属性.这里我们将专家ek表达的确定分级区间直觉模糊评价系统表示为Sk={A, C, d, fk},其中fk:A×(C∪{d})→II∪G是信息函数,且II是区间直觉模糊数集,G={g1, g2, …, gs}为初步划分等级.
2.1 基于评价一致相似度的专家权重确定第k个专家的初步分级评价信息可视为对象集上的等级映射,记为fdk:A×{d}→G,则涉及的l个专家的等级映射对应的优势粒结构分别为Rfd1, Rfd2, …, Rfdl,则计算两两专家的初步评价的相似度矩阵为
| $ \mathit{\boldsymbol{SM}} = \left( {\begin{array}{*{20}{c}} {sim\left( {{R_{f_d^1}},{R_{f_d^1}}} \right)}&{sim\left( {{R_{f_d^1}},{R_{f_d^2}}} \right)}& \cdots &{sim\left( {{R_{f_d^1}},{R_{f_d^l}}} \right)}\\ {sim\left( {{R_{f_d^2}},{R_{f_d^1}}} \right)}&{sim\left( {{R_{f_d^2}},{R_{f_d^2}}} \right)}& \cdots &{sim\left( {{R_{f_d^2}},{R_{f_d^l}}} \right)}\\ \vdots&\vdots &{}& \vdots \\ {sim\left( {{R_{f_d^l}},{R_{f_d^1}}} \right)}&{sim\left( {{R_{f_d^l}},{R_{f_d^1}}} \right)}& \cdots &{sim\left( {{R_{f_d^l}},{R_{f_d^l}}} \right)} \end{array}} \right). $ | (4) |
与其他专家评价一致性高的专家应获得比较高的权重,而评价与群体偏离的专家应赋予较低的权重,根据这一设定权重思想,设定专家ek的权重为
| $ {\rho ^k} = \left( {\sum\limits_{{k_1} = 1,{k_1} \ne k}^l {sim\left( {{R_{f_d^k}},{R_{f_d^k1}}} \right)} } \right)/\left( {\sum\limits_{{k_1} = 1}^l {\sum\limits_{{k_2} = 1,{k_2} \ne {k_1}}^l {sim\left( {{R_{f_d^k1}},{R_{f_d^k2}}} \right)} } } \right), $ | (5) |
其中
给定专家ek评价系统Sk={A, C, d, fk},系统中既有专家在各个属性下的区间直觉模糊值定量评价,也有在决策属性下的定性等级评价.在实际决策过程中,相同属性在不同的专家看来具有不同的重要性,因此这里我们认为属性权重在不同的评价系统中应该具有相异性.设系统Sk中属性集C的权重向量记为Wk=(w1k, w2k, …, wmk),下面设定属性权重使得评价结果与专家的初步评价结果保持一致.
系统Sk中,所有对象对A×A中的n×n个对象分为两类:占优类Pdk={(ai, aj) fk(ai, d)>fk(ai, d)}和被占优类Qdk={(ai, aj) fk(ai, d) < fk(ai, d)}.根据实际意义,Pdk=(Qdk)-1占有类与被占有类之间具有关联性,在下列的模型中我们仅考虑被占优类. Sk中对象在属性cj下的区间直觉模糊取值构成区间直觉模糊数集,根据第1节给出的区间直觉模糊相对大于度计算出相应的相对大于可能度矩阵为
| $ \mathit{\boldsymbol{M}}_j^k = \left( {\begin{array}{*{20}{c}} {p_{11}^{k,j}}&{p_{12}^{k,j}}& \cdots &{p_{1n}^{k,j}}\\ {p_{21}^{k,j}}&{p_{22}^{k,j}}& \cdots &{p_{2n}^{k,j}}\\ \vdots&\vdots &{}& \vdots \\ {p_{n1}^{k,j}}&{p_{n1}^{k,j}}& \cdots &{p_{nn}^{k,j}} \end{array}} \right), $ | (6) |
其中:pstk, j=P(fk(as, cj), fk(at, cj)).设定属性权重,使得综合相对大于可能度与专家的初步评价尽可能一致,因此建立最优一致模型
| $ \mathit{min}\;{B^k} = \sum\limits_{\left( {{a_s},{a_t}} \right) \in {Q^k}} {\sum\limits_{j = 1}^m {w_j^kp_{st}^{k,j}} } ,\;\;{\rm{s}}.\;{\rm{t}}.\;\;w_j^k \in \left[ {0,1} \right],\;\;\;\sum\limits_{j = 1}^m {{{\left( {w_j^k} \right)}^2}} = 1. $ | (7) |
根据以上模型可确定第k个专家的属性权重向量,在群决策中,l个专家就需要建立l个优化模型计算l组权重向量.求得不同专家属性的权重Wk=(w1k, w2k, …, wmk)后,将以上的各系统中不同属性下的区间直觉模糊相对大于度矩阵进行加权求和,有
| $ {\mathit{\boldsymbol{M}}^k} = \sum\limits_{j = 1}^m {w_j^k} \mathit{\boldsymbol{M}}_j^k. $ | (8) |
基于优势粒结构相似度的专家权重,结合考虑每个专家初步分级判断的属性权重,我们给出具有确定分级偏好区间直觉模糊表达多属性群决策方法的计算步骤.
输入:l个专家的评价系统Sk=(A, C, d, fk)(k=1, 2, …, l);
输出:对象的排序向量及排序结果;
步骤1 计算每个评价系统下初步分级评价对应的优势粒结构Rfdk(k=1, 2, …, l);
步骤2 运用公式(3)和(4)计算专家评价一致矩阵SM;
步骤3 运用公式(5)计算专家权重(ρ1, ρ2, …, ρl);
步骤4 根据公式(1)计算评价系统Sk(k=1, 2, …, l)中属性cj(j=1, 2, …, m)下的区间直觉模糊数相对大于可能度矩阵Mjk;
步骤5 根据公式(7)计算系统Sk(k=1, 2, …, l)中的属性权重向量Wk=(w1k, w2k, …, wmk);
步骤6 根据公式(8)集结步骤5的权重向量与步骤4中大于可能度矩阵得Mk;
步骤7 结合步骤3中的专家权重计算得综合专家的大于可能度矩阵
步骤8 根据公式(2)计算每个对象的综合排序向量.
4 人力资源管理求解实例某企业欲从新聘任大学生中选择1人作为外联部门后备干部进行培养,召集4个部门的负责人对5名学生进行考评和选拔,这是一个多属性群决策问题,企业人力资源部门邀请4位专家(人事部门负责人e1、HR猎头专家e2、业务部门主任e3和外联部门主任e4),对5个大学生(记为a1, a2, a3, a4, a5)的基本情况进行评价.人员的评价指标涉及个人语言表达能力(c1)、业务水平(c2)、分析解决问题能力(c3)、英文水平(c4).各专家通过考核对5名人员在各个指标下给出区间直觉模糊数评价信息,对5个人的初级评价d分别设为:推荐(Y)、不推荐(N)、犹豫(U). 表 1~4为专家对各个人员的带初步分级决策信息的评价表.
|
|
表 1 专家e1带分级信息的评价系统 Tab. 1 Evaluation system with sorting information provided by e1 |
|
|
表 2 专家e2带分级信息的评价系统 Tab. 2 Evaluation system with sorting information provided by e2 |
|
|
表 3 专家e3带分级信息的评价系统 Tab. 3 Evaluation system with sorting information provided by e3 |
|
|
表 4 专家e4带分级信息的评价系统 Tab. 4 Evaluation system with sorting information provided by e4 |
运用第3节算法计算确定最后的靠近选拔结果.
步骤1 计算4个专家初步分级评价精确粒结构分别为
| $ {R_{f_d^1}} = \left\{ {A,\left\{ {{a_2},{a_3}} \right\},\left\{ {{a_3}} \right\},A,A} \right\}, \cdots ,{R_{f_d^4}} = \left\{ {\left\{ {{a_1},{a_2}} \right\},\left\{ {{a_1},{a_2}} \right\},A,A,A} \right\}. $ |
步骤2 根据公式(3)和(4),计算专家评价一致矩阵SM为
步骤3 根据公式(5)计算专家的权重分别为ρ1=0.17, ρ2=0.32, ρ3=0.32, ρ1=0.19.
步骤4 需计算4个评价系统中4个属性下的区间直觉模糊大于可能度矩阵Mk, j, 分别为
| $ \mathit{\boldsymbol{M}}_1^1 = \left( {\begin{array}{*{20}{c}} {0.50}&{0.88}&{0.44}&{0.94}&{0.79}\\ {0.12}&{0.50}&{0.63}&{0.56}&{0.42}\\ {0.56}&{0.37}&{0.50}&{1.00}&{0.85}\\ {0.06}&{0.44}&{0.00}&{0.50}&{0.35}\\ {0.21}&{0.58}&{0.15}&{0.65}&{0.50} \end{array}} \right), \cdots ,\mathit{\boldsymbol{M}}_4^4 = \left( {\begin{array}{*{20}{c}} {0.50}&{0.00}&{0.30}&{0.30}&{0.00}\\ {1.00}&{0.50}&{0.80}&{0.80}&{0.50}\\ {0.70}&{0.20}&{0.50}&{0.50}&{0.20}\\ {0.70}&{0.25}&{0.50}&{0.50}&{0.20}\\ {1.00}&{0.50}&{0.80}&{0.80}&{0.50} \end{array}} \right). $ |
步骤5 根据以上16个相对大于可能度矩阵,建立优化模型计算4个系统中属性权重分别为
| $ {\mathit{\boldsymbol{W}}^1} = \left( {0.31,0.22,0.29,0.18} \right),{\mathit{\boldsymbol{W}}^2} = \left( {0.23,0.28,0.22,0.28} \right), $ |
步骤6 结合步骤5权重对大于可能度矩阵进行集结得到
| $ {\mathit{\boldsymbol{W}}^3} = \left( {0.21,0.26,0.24,0.29} \right),{\mathit{\boldsymbol{W}}^4} = \left( {0.15,0.33,0.29,0.23} \right). $ |
步骤7 结合专家权重得对象的大于可能度矩阵
| $ {\mathit{\boldsymbol{M}}^1} = \left( {\begin{array}{*{20}{c}} {0.50}&{0.31}&{0.30}&{0.50}&{0.53}\\ {0.67}&{0.50}&{0.49}&{0.69}&{0.71}\\ {0.70}&{0.51}&{0.50}&{0.70}&{0.72}\\ {0.50}&{0.31}&{0.30}&{0.50}&{0.53}\\ {0.47}&{0.29}&{0.28}&{0.47}&{0.50} \end{array}} \right), \cdots ,{\mathit{\boldsymbol{M}}^4} = \left( {\begin{array}{*{20}{c}} {0.50}&{0.34}&{0.40}&{0.52}&{0.40}\\ {0.66}&{0.50}&{0.56}&{0.67}&{0.56}\\ {0.60}&{0.44}&{0.50}&{0.61}&{0.50}\\ {0.48}&{0.32}&{0.39}&{0.50}&{0.39}\\ {0.60}&{0.44}&{0.50}&{0.61}&{0.50} \end{array}} \right). $ |
步骤8 根据公式(2)计算得5个对象的排序分量是0.214 3, 0.213 5, 0.224 7, 0.180 8, 0.166 7,因此可知a3>a1>a2>a4>a5.
群决策的结果是a3综合评价为第一.与文献[5-8]相比,提出的方法在预备阶段将区间直觉模糊数的表达转化为评价表达下的大于可能度矩阵,通过对象的相对比较信息建立模型获得对象序.该算法不依赖于直觉模糊算子的集结方法,不需要决策者提前给定权重,是一种纯客观评价数据驱动的新方法.
5 总结本文针对评价信息为区间直觉模糊信息的多属性群决策问题,提出一种数据驱动,无需决策者表达权重偏好信息的客观方法.该模型能够将决策数据与专家粗粒度的初步分级评价信息有效结合,无论属性还是专家权重,均从数据出发计算一致度确定客观权重,最优模型有机结合了评价数据与专家的主观分级偏好.实例计算说明模型是有效的.
| [1] |
徐泽水. 直觉模糊信息集成理论与应用[M]. 北京: 清华大学出版社, 2007.
(  0) 0) |
| [2] |
ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy sets and systems, 1986, 20(1): 87-96. DOI:10.1016/S0165-0114(86)80034-3 (  0) 0) |
| [3] |
袁芳, 周小强, 胡满佳. 广义直觉模糊软集及其代数性质[J]. 郑州大学学报(理学版), 2012, 44(4): 46-49. DOI:10.3969/j.issn.1671-6841.2012.04.010 (  0) 0) |
| [4] |
YE J. Multicriteria fuzzy decision-making method using entropy weights-based correlation coefficients of interval-valued intuitionistic fuzzy sets[J]. Applied mathematical modelling, 2010, 34(12): 3846-3870. (  0) 0) |
| [5] |
LIU P D. Some Hamacher aggregation operators based on the interval-valued intuitionistic fuzzy numbers and their application to group decision making[J]. IEEE transactions on fuzzy systems, 2014, 22(1): 83-97. DOI:10.1109/TFUZZ.2013.2248736 (  0) 0) |
| [6] |
JIN F F, LIU P D, CHEN H Y, et al. Interval-valued intuitionistic fuzzy continuous weighted entropy and its application to multi-criteria fuzzy group decision making[J]. Knowledge-based systems, 2014, 59(2): 132-141. (  0) 0) |
| [7] |
LAKSHMANA GOMATHI NAYAGAM V, JEEVARAJ S, DHANASEKARAN P. An intuitionistic fuzzy multi-criteria decision-making method based on non-hesitance score for interval-valued intuitionistic fuzzy sets[J]. Soft computing, 2017, 21(23): 7077-7082. DOI:10.1007/s00500-016-2249-0 (  0) 0) |
| [8] |
梁吉业, 王宝丽. 基于粗糙集的多属性群决策方法[M]. 南京: 南京大学出版社, 2012: 131-146.
(  0) 0) |
| [9] |
WANG B L, LIANG J Y, QIAN Y H. Determining decision makers′ weights in group ranking: a granular computing method[J]. International journal of machine learning and cybernetics, 2015, 6(3): 511-521. DOI:10.1007/s13042-014-0278-5 (  0) 0) |
| [10] |
徐泽水. 不确定多属性决策方法及应用[M]. 北京: 清华大学出版社, 2004.
(  0) 0) |
 2019, Vol. 51
2019, Vol. 51

