2. 中铁隧道集团勘测设计研究院 河南 洛阳 471009;
3. 中铁重庆地铁建设指挥部 重庆 401120
2. Survey, Design and Research Institute of China Railway Tunnel Group, Luoyang 471009, China;
3. China Railway Chongqing Subway Construction Headquarters, Chongqing 401120, China
随着城市人口的不断增加,解决城市交通拥堵也迫在眉睫,城市地铁是解决这一问题的有效措施[1-2].城市地铁线路的增多,多线路交汇处就需要更大断面隧道来满足[3],本文的依托工程为单拱4线地铁隧道,断面开挖面积近400 m2,属于超大断面隧道[4].城市轨道交通建设由于在构筑物密集和交通繁忙的区域,需要修建断面大、埋深浅的地下工程,同时由于埋深浅,又要满足多线路大断面的要求,因此,断面设计扁平率越来越小[5-8].扁平大断面隧道势必成为未来隧道建设解决高密度交通流量的隧道结构形式.
扁平隧道围岩受力相比椭圆形隧道断面结构形式复杂,选取合适的扁平率对于超大扁平隧道的设计显得尤为重要,优化后的扁平率隧道断面能够在保证安全的条件下,满足功能需要、节省空间以及增强围岩稳定性.文献[4-8]在对隧道结构断面形状进行优化时,分别采用应力最小、围岩破坏面积、围岩变形位移、隧道建造造价、隧道净空面积和轮廓周长作为目标函数的单目标函数寻优方法.隧道断面优化不仅仅考虑应力、围岩破坏面积、位移以及断面几何尺寸等作为单一目标函数,隧道断面的选择应该综合考虑安全、技术以及经济等多因素影响.断面的优化也逐渐向多目标优化发展,能够综合考虑多种因素,对施工安全以及成本的控制起着关键性的作用.
本文采取层次分析法理论[9-10],对超大断面隧道的断面设计进行了优化.利用有限元分析软件ANSYS分析5种不同扁平率超大断面隧道开挖后的应力分布、位移分布、衬砌受力等;采用地表沉降、初支受力、隧道围岩变形等指标,对超大断面隧道扁平率进行优化分析.并将最终采取的断面形式现场检测数据与计算数据进行对比分析,验证了计算模型的合理性与优化结果的可靠性.
1 工程背景及监测方案重庆轨道交通5号线3标工程位于重庆市北部新区,隧道起始里程为DK18+138.948~DK18+191.964,区间隧道为单拱4线地铁隧道,钻爆开挖,衬砌为复合式衬砌,为国内在建轨道交通工程最大跨度暗挖区间隧道.区间线路所经地段的原始地貌属构造剥蚀丘陵区.沿线海拔高程290~375 m之间,相对高差85 m左右.隧道开挖断面所处岩层主要为砂质泥岩,等级为Ⅳ级.隧道开挖空间最大高度近17.2 m,跨度27.6 m,总开挖面积近388.47 m2,为浅埋扁平超大断面隧道.
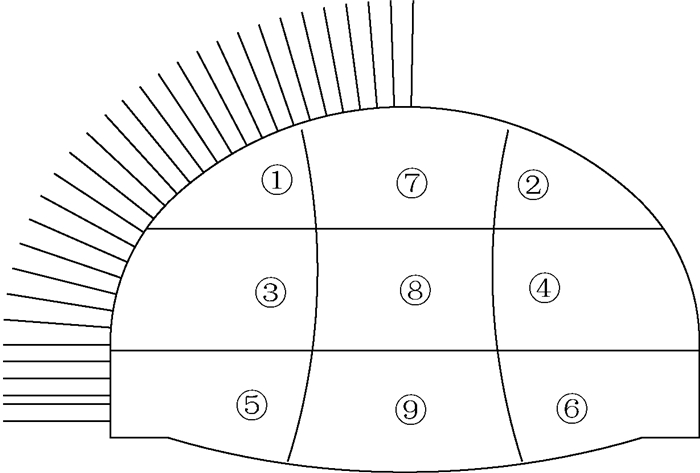
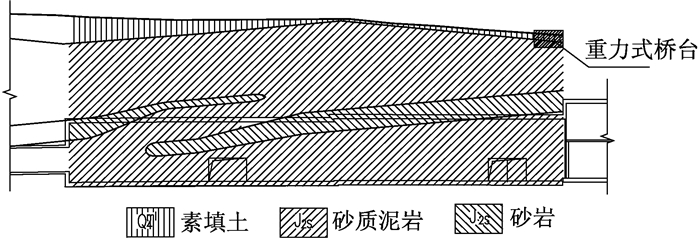
采用9部开挖的双侧壁导坑法施工,施工工序见图 1.喷射早强混凝土采用C25混凝土,厚度为30 cm,I25 b工字钢钢架,纵向间距0.5 m.二次衬砌采用C40钢筋混凝土,厚度为100 cm,二衬钢筋为HRB400、HRB300钢筋,仰拱采用C20钢筋混凝土填充.地质纵剖面见图 2.
|
图 1 施工工序图 Figure 1 Construction process diagram |
|
图 2 地质纵剖面图 Figure 2 Geological profile |
监测方案:大跨浅埋扁平段隧道总长52.993 m,水平净空收敛和拱顶下沉测点设置3个测试断面,地表沉降测点每隔10 m一个断面,每断面6个测点,每测点间隔8 m.
2 有限元数值模拟与对比方案设计 2.1 计算假定与数值模型采用有限元分析软件ANSYS15.0建立二维单元模型,采用“地层-结构”模型和Drucker-Prager屈服准则.
计算模型两侧围岩选用2倍洞径宽度,隧道顶部取大于3倍洞径,底部围岩取2倍洞径作为有限元分析范围.围岩和混凝土单元采用平面单元Plane42;钢拱架及喷射混凝土采用Beam3梁单元;锚杆采用Link1线单元模拟;输入不同材料的物理力学参数进行模拟,隧道围岩力学参数见表 1.
|
|
表 1 隧道围岩及结构材料基本力学参数 Table 1 Basic mechanical parameters of tunnel surrounding rock and structural |
隧道开挖采用9部双侧壁导坑法,采用ANSYS程序中的荷载步功能模拟隧道开挖施工,其中需要采用单元生死技术模拟隧道的开挖以及支护过程.本文对隧道的施工过程进行了动态模拟,包括围岩的开挖、施作喷射混凝土初期支护、钢拱架支撑、锚杆支护、临时支护以及二次衬砌结构施作,共19个荷载步.在隧道工程中,隧道开挖为应力释放过程,这里假定隧道开挖结束后初期支护承受了70 %的荷载[11].约束数值模型左右边界的水平向位移,顶部位移释放为自由边界,约束隧道底部边界的竖向位移.
2.2 隧道断面参数根据依托工程背景,为了研究不同扁平率的影响,在不改变隧道断面宽度,只改变隧道断面高度的方法,确定了5种扁平率分别为0.56、0.60、0.63、0.66、0.70,隧道高度分别对应为15~19 m,每个扁平率断面高度增加1 m,5种扁平率用C1~C5依次代表.
3 计算结果分析及与监测数据对比分析 3.1 不同扁平率数值仿真结果分析从计算结果云图来看,5种不同扁平率隧道断面结构力学特征规律基本一致,只给出5种扁平率围岩应力分布云图.其他分析选取扁平率为0.63时隧道断面计算结果.
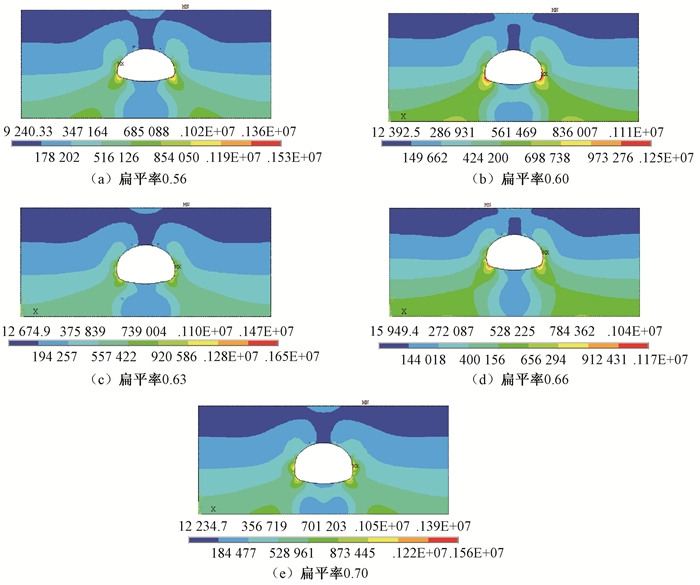
对比图 3中5种不同扁平率围岩应力云图可知,扁平率对围岩应力的影响比较大,最大应力位置随扁平率的变化而变化.扁平率为0.7时,围岩最大应力发生在拱腰位置;扁平率为0.56时,围岩最大应力位置在拱脚处,而拱腰处受力不再最大;最大应力位置随着扁平率的减小逐渐下移.这是由于,随着扁平率的减小,隧道拱顶受力作用面增大,其最大受力位置下移.
|
图 3 不同扁平率隧道围岩von Mises stress云图 Figure 3 von Mises stress of tunnel surrounding rock with different flat rate |
由图 3可以看出,最大应力范围也随扁平率的减小而逐渐增大,说明扁平率的减小,对围岩影响增大.当扁平率为0.56时,隧道的开挖对隧道周围围岩较大范围产生影响,由于隧道拱脚承受较大弯矩,拱脚附近围岩受影响较大,拱顶以及拱腰附近围岩受影响也较大,围岩达到塑性界限就会发生塑性变形,引起围岩过大变形,可见扁平率为0.56时较为危险,其余4种扁平率对围岩的影响范围较小.
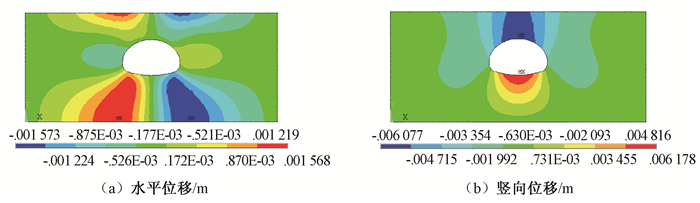
从图 4看出水平位移对称分布,水平位移最大位置位于隧道两侧拱肩和两侧拱脚位置,隧道正上方左右两侧位置地表水平位移较大.拱顶中间竖向变形最大下沉量为6.077 mm,仰拱隆起量为6.178 mm;由于该大断面扁平隧道为浅埋,浮力对地层位移有一定的影响,造成仰拱的隆起.
|
图 4 扁平率为0.63时围岩位移云图 Figure 4 The displacement of surrounding rock with the flat rate of 0.63 |
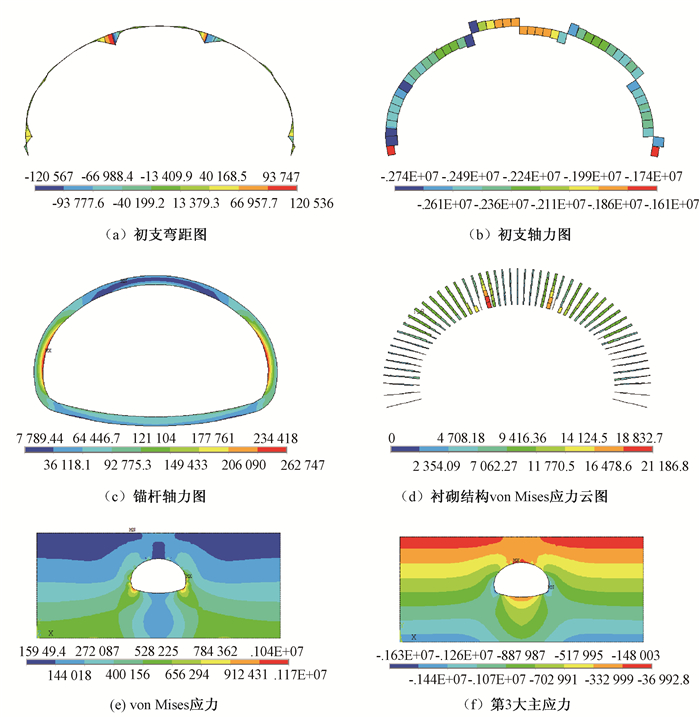
图 5(a)为钢拱架弯矩图,从图中可看出,拱顶部两侧临时支撑点有较大弯矩,这是由于中隔墙开挖较晚,支撑点两侧围岩位移不协调发展,造成该处钢拱架承受较大弯矩.钢拱架的支撑作用,调整了整个钢拱架弯矩分布,避免了较大弯矩的产生,使得弯矩分布较为均匀,整体来看拱脚以及拱腰部位弯矩较大,最大正弯矩为120.536 (kN·m),最大负弯矩为120.567 (kN·m),均处于两侧拱顶位置的应力集中处.若除去该处钢拱架支撑的影响,整个隧道拱架的拱脚弯矩最大,最大值为40.321 (kN·m),拱顶弯矩为13.461 (kN·m).
|
图 5 扁平率为0.63时受力分布云图 Figure 5 The stress distribution cloud pictures with a flat rate of 0.63 |
从图 5(b)可知,钢拱架最大轴力在拱脚处,承受压力,最大轴力为2 740 kN.
从图 5(c)知,当中隔墙开挖完成后,拱顶受中隔墙支撑区下沉,导致中隔墙两侧锚杆受拉力较大,锚杆整体承受拉力,整体来看,拱腰偏上部位锚杆受力较大,拱脚部位锚杆拉力为4.7 kN,拱腰偏上部位锚杆轴力在10.0 kN左右,由于扁平隧道顶部受力作用面较大,造成拱腰偏上部位锚杆受力较大.
从图 5(d)看出,衬砌结构在拱顶和拱腰位置应力较大,最大应力0.27 MPa.
图 5(e)、(f)分别为隧道开挖完成后围岩von Mises应力云图、围岩第3大主应力云图.可以看出,应力最值均出现在拱腰以及拱顶位置;最大von Mises应力出现在拱腰,值为1.17 MPa;第3大主应力最值出现在拱腰位置值为1.63 MPa.因此在隧道开挖后,应对拱腰位置进行加强支护.
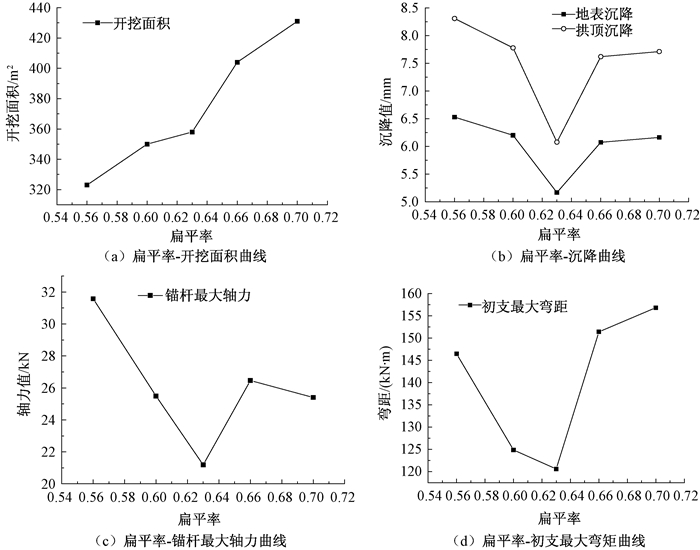
从图 6(a)知,在Ⅳ级围岩条件下,隧道开挖面积与扁平率成正相关.随着扁平率的增大,开挖面积增大,施工成本增大,因此开挖面积将作为断面优化的一个指标,能够很好地控制施工成本.
|
图 6 各指标随扁平率变化曲线 Figure 6 The change curves of each index with the flat rate |
从图 6(b)看出,拱顶沉降曲线与地表沉降曲线规律一致.隧道开挖后,拱顶下沉值与扁平率不存在单一线性关系,在扁平率为0.63时,拱顶沉降值最小,为6.077 mm;除去扁平率为0.63时来看,沉降值随扁平率的减小而增大,因而在减小隧道断面扁平率的情况下,应当着重控制地表沉降和拱顶沉降.地表沉降、拱顶沉降都是施工监测的重点对象,关系着隧道施工的安全,对断面设计的优化将地表沉降、拱顶沉降作为优化指标,能够保证安全.
从图 6(c)看出,锚杆轴力在扁平率为0.56时,达到峰值.最小值为扁平率为0.63时,除去该点,整体来看,锚杆最大轴力随扁平率的减小而增大.
从图 6(d)知,初期支护弯矩,在扁平率为0.63时最小,值为120.567 (kN·m).弯矩变化规律与沉降曲线和锚杆轴力曲线有所不同,随着扁平率的增大,最大初支弯矩是增大的.
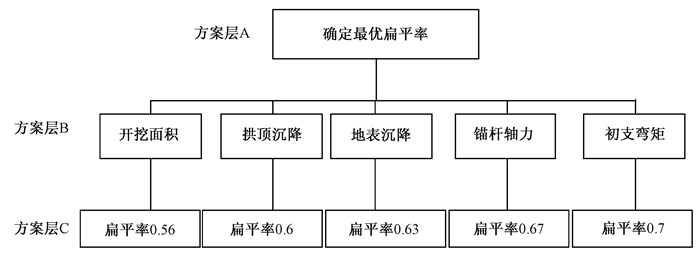
3.2 基于层次分析法的隧道断面扁平率优化结果层次分析法属于运筹学理论.该方法将思维过程数学化,从而为复杂的决策问题提供一种简单、实用的多准则决策的评价方法[12].以锚杆轴力、初支最大弯矩、拱顶沉降、地表沉降及断面开挖面积为判断准则,在保持隧道跨度不变前提下,对超大断面隧道断面设计优化.隧道断面优化层次模型见图 7.
|
图 7 隧道断面优化层次模型 Figure 7 Optimization model of tunnel section |
隧道开挖优化目标函数值见表 2.
|
|
表 2 不同扁平率隧道开挖优化目标函数值 Table 2 Optimization objective function of tunnel excavation with different flat rate |
最终通过层次总排序及一致性检验计算结果见表 3.
|
|
表 3 权重求解结果 Table 3 Weight solving result |
通过一致性检验及权重求解结果知扁平率0.63为5种方案中最优的.
3.3 数值计算结果与监测数据对比分析重庆轨道交通5号线3标段浅埋扁平超大断面隧道最终采用了优化设计的扁平率为0.63的断面形状,以上5种数值计算结果均为模拟分析,为了验证计算模拟的可靠性,将数值计算结果与现场监测数据进行对比分析.
从表 4知,实测值比计算值稍大,经分析主要存在以下原因:1)隧道地表线路原始地貌属构造剥蚀丘陵区,经人工后期改造为城市主干道,且地层有人工填土,在雨水的作用下实际地表沉降值比数值计算数据大;2)现场施工条件复杂、爆破等开挖对周围围岩有一定扰动;3)重庆地区雨水较多,地下水丰富,地下水对隧道围岩稳定性有一定影响;4)双侧壁导坑法分部多,施工步序繁杂,现场施工断面不能及时进行支护封闭成环.
|
|
表 4 计算值与实测值对比数据 Table 4 Comparison of calculated and measured data |
整体来看实测值与计算值数量级相当,数值模型计算结果合理,浅埋超大断面扁平率优化结果0.63合理.
4 结论1) 分析了不同扁平率下隧道力学特性,对于扁平隧道,随着扁平率的减小,隧道围岩拱顶受力作用面增大,引起拱腰受力较大,位置不断下移,拱脚应力集中,隧道围岩受力分布规律随之变化,因而对于扁平隧道应当加强拱脚及边墙的强度.
2) 从不同扁平率各个指标曲线可知,地表沉降、拱顶沉降、锚杆轴力、初支弯矩与扁平率并不呈现单一的线性关系,通过分析可以确定一个较为合适的扁平率,能够满足安全和节约成本的要求.
3) 采用层次分析法对浅埋扁平大断面隧道扁平率进行了多目标优化研究,相比传统单目标寻优的方法,综合考虑了多方面因素,结果表明,扁平率为0.63的断面形式为最优方案.
4) 将最终采取的扁平率优化结果0.63情形下的数值计算结果与现场监测数据进行了对比分析,验证了计算模型以及优化结果的可靠性.
| [1] |
施有志, 李建峰, 李汪颖, 等. 扁平超大断面隧道的施工力学特征及其动力稳定性分析[J]. 上海交通大学学报, 2015, 49(7): 1023-1029. (  0) 0) |
| [2] |
张洵安, 王显彬. 软岩隧道开挖与支护的三维有限元仿真分析[J]. 郑州大学学报(工学版), 2008, 29(2): 139-144. (  0) 0) |
| [3] |
吕爱钟. 地下洞室最优开挖形状的确定方法[J]. 岩石力学与工程学报, 1996, 15(3): 275-281. (  0) 0) |
| [4] |
王建, 胡潇月. 特大断面公路隧道扁平率数值分析[J]. 公路交通技术, 2014, 6(3): 90-94. (  0) 0) |
| [5] |
陈卫忠, 王辉, 田洪铭. 浅埋破碎岩体中大跨隧道断面扁平率优化研究[J]. 岩石力学与工程学报, 2011, 30(7): 1390-1395. (  0) 0) |
| [6] |
杨万斌, 薛玺成. 地下洞室的间距和断面优化计算方法[J]. 岩土工程学报, 2001, 23(1): 61-63. (  0) 0) |
| [7] |
徐林生, 孙钧, 蒋树屏. 洋碰隧道断面形状设计优化问题研究[J]. 岩土工程技术, 2001, 3: 181-184. (  0) 0) |
| [8] |
蔡新, 李洪煊, 武颖利, 等. 水下隧道结构优化设计[J]. 河海大学学报(自然科学版), 2009, 37(6): 666-668. (  0) 0) |
| [9] |
王爱领. 基于改进的Vague-Topsis方法的公租房轮候排序评价研究[J]. 郑州大学学报(理学版), 2013, 45(3): 116-119. (  0) 0) |
| [10] |
王刚, 罗勇. 基于专家可信度的熵权-AHP建筑施工企业信用评价[J]. 郑州大学学报(理学版), 2015, 47(3): 122-126. (  0) 0) |
| [11] |
李围. 隧道及地下工程ANSYS实例分析[M]. 北京: 中国水利水电出版社, 2007.
(  0) 0) |
| [12] |
王连芬. 层次分析法引论[M]. 北京: 中国人民大学出版社, 1990.
(  0) 0) |
 2017, Vol. 49
2017, Vol. 49


