0 引言

高超声速飞行器(hypersonic vehicle, HV)，在本文中简称为高速飞行器，飞行速度不小于5马赫，是一种具有强耦合、强非线性的复杂对象^[1-3]，在军事上和民用上具有广阔的应用前景^[4]。高速飞行器再入段的姿态控制成为了各国航空航天领域的难点和热点。高速飞行器再入段的初期由于大气密度较低，气动舵面效率不足^[5-6]，需要反作用控制系统(reaction control system, RCS)维持姿态稳定^[7-8]。RCS系统执行器为一组推力恒定的脉冲型推力器^[9]。为了提高飞行器的稳定性，降低故障影响^[10-11]，一般设计为冗余配置。但是冗余配置增加了指令分配的难度，且有可能造成燃料的浪费。因此有必要进行RCS控制分配方法研究。

文献[12]对于多操纵面的战机出现未知执行器故障的情况，设计了一种自适应容错控制分配方法。文献[13]中设计了基于线性规划的优化控制分配方法来进行舵面和RCS的控制分配。文献[14-15]都研究了基于零空间的再分配伪逆法。其中，再分配伪逆法在初解阶段能够获得最优解，但是经过再分配后得到的解已经不满足最优情况，且伪逆法的实时性也难以保证。为了减少燃料的消耗且保证控制分配算法的实时性，本文创新性地提出了一种改进的具有固定推力器开启数的再分配伪逆法，并将其应用于高速飞行器再入段飞行姿态控制。

本文首先建立了高速飞行器再入段系统模型，分析了RCS系统的配置情况。之后针对临近空间高速飞行器再入段姿态模型，设计有限时间终端滑模控制(terminal sliding mode control, TSMC)算法，实现姿态跟踪控制。又对给定8推力器配置的RCS系统进行3推力器开启的再分配伪逆法改进设计，以减少燃料消耗和保证控制分配算法实时性。最后通过仿真验证了所设计控制系统的有效性。

1 高速飞行器RCS系统建模

本文建立的高速飞行器模型参考了文献[16]的Winged-Cone模型和文献[17]的飞行器模型。本文的研究对象是一类有翼圆锥体高速飞行器，其反作用控制系统为8推力器配置且具有恒定推力的一组推力器。

1.1 高速飞行器模型

高速飞行器再入过程运动学方程如式(1)~(13)所示，

$ {\dot x = V\cos \theta \cos \sigma ,} $

(1)

$ {\dot y = V\sin \theta ,} $

(2)

$ {\dot z = - V\cos \theta \sin \sigma ,} $

(3)

$ {\dot V = - \frac{D}{m} + \frac{g}{r}(x\cos \sigma \cos \theta + (y + R)\sin \theta - z\sin \sigma \cos \theta ),} $

(4)

$ {\dot \theta = \frac{{L\cos \mu - Y\sin \mu }}{{mV\cos \sigma }} + \frac{g}{{rV\cos \sigma }}[ - x\cos \sigma \sin \theta + (y + R)\cos \theta + z\sin \sigma \sin \theta ],} $

(5)

$ {\dot \sigma = - \frac{{L\sin \sigma + Y\cos \sigma }}{{mV}} - \frac{g}{{rV}}(x\sin \sigma + z\cos \sigma ),} $

(6)

$ {g = {g_0}{{\left( {\frac{R}{{R + h}}} \right)}^2},} $

(7)

$ {{{\dot \omega }_x} = \frac{{\left( {{I_y} - {I_z}} \right)}}{{{I_x}}}{\omega _y}{\omega _z} + \frac{1}{{{I_x}}}\left( {{l_A} + {l_{{\rm{RCS}}}}} \right),} $

(8)

$ {{{\dot \omega }_y} = \frac{{\left( {{I_z} - {I_x}} \right)}}{{{I_y}}}{\omega _x}{\omega _z} + \frac{1}{{{I_y}}}\left( {{m_A} + {m_{{\rm{RCS}}}}} \right),} $

(9)

$ {{{\dot \omega }_z} = \frac{{\left( {{I_x} - {I_y}} \right)}}{{{I_z}}}{\omega _x}{\omega _z} + \frac{1}{{{I_z}}}\left( {{n_A} + {n_{{\rm{RCS}}}}} \right),} $

(10)

$ {\dot \alpha = {\omega _z} - {\omega _x}\cos \alpha \tan \beta + {\omega _y}\sin \alpha \tan \beta - \frac{1}{{mV\cos \beta }}(L + mg\cos \theta \cos \mu ),} $

(11)

$ {\dot \beta = {\omega _x}\sin \alpha + {\omega _y}\cos \alpha + \frac{1}{{mV}}(L - mg\cos \theta \sin \mu ),} $

(12)

$ {\dot \mu = {\omega _x}\frac{{\cos \alpha }}{{\cos \beta }} - {\omega _y}\frac{{\sin \alpha }}{{\cos \beta }} + \frac{1}{{mV}}[L(\sin \theta \sin \mu + \tan \beta ) + C\sin \theta \cos \mu + mg\cos \theta \cos \mu \tan \beta ],} $

(13)

式中：x、y、z分别为高速飞行器在惯性坐标系下的坐标；V、θ、σ分别为速度、飞行倾角和飞行偏角；h、m分别为飞行高度和质量；g为当地重力加速度；r为飞行器质心在惯性坐标系中的矢径；常量R为地球半径；ω_x、ω_y、ω_z分别为HV的滚转、偏航和俯仰角速度；I_x、I_y、I_z分别为x、y、z轴的转动惯量；D、L、C分别为阻力、升力和侧向力；l_A、m_A、n_A分别为三轴气动力矩；l_RCS、m_RCS、n_RCS分别为RCS系统提供的三轴力矩；α、β、μ为攻角、侧滑角和速度滚转角。高速飞行器再入段气动方程和系数参考了文献[18]。

将与姿态有关的6个方程(8)~(13)提取出，改写成仿射非线性形式^[19]，见式(14)~(15)。

$ \dot{\boldsymbol{\varOmega}}=\boldsymbol{f}_{o}+\boldsymbol{g}_{o} \boldsymbol{\omega}, $

(14)

$ \dot{\boldsymbol{\omega}}=\boldsymbol{f}_{i}+\boldsymbol{g}_{i} \boldsymbol{M}, $

(15)

其中: Ω=[α; β; μ]是姿态角度; ω=[ω_x; ω_y; ω_z]是姿态角速度; M=[l_A+l_RCS; m_A+m_RCS; n_A+n_RCS]是三轴力矩；f_o、f_i、g_o、g_i为对应系数矩阵。

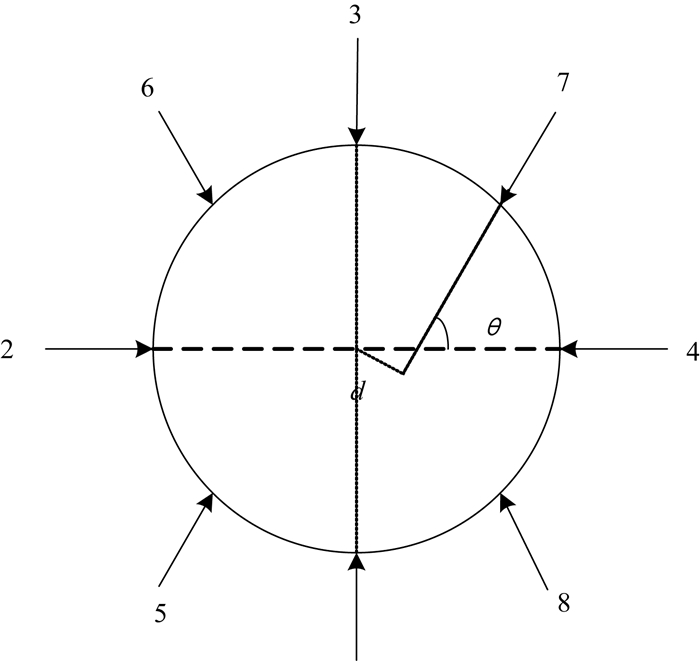
1.2 RCS系统配置分析

RCS采取冗余设计，即RCS的推力器个数大于飞行器的自由度。例如，文献[20]中提到哥伦比亚航天飞机的RCS系统采用44推力器设计。为减小RCS的设计载荷，本文研究的飞行器RCS由8个推力器组成，安装在飞行器尾端。结构如图 1所示。每个推力器的推力均恒为1 500 N。

设推力器安装角度为θ_r，距离质心安装距离为d，到质心的距离为L_r。其中: L_r=4 m；d=0.5 m；θ_r=60°；F=1 500 N。则推力器能提供的三轴的力矩大小如表 1所示。

2 高速飞行器再入段姿态控制系统

在高速飞行器再入段姿态控制系统设计中，由于姿态模型的各个变量在时间尺度上具有明显差异，将飞行器的状态变量分为快、慢不同回路，分别设计控制算法。本文采用有限时间终端滑模控制。高速飞行器再入姿态控制系统结构如图 2所示。

在图 2中的双环终端滑模姿态控制器中，外环为慢回路，其输入为期望的姿态角速度ω_c=[ω_xc; ω_yc; ω_zc]^T，跟踪的指令为制导系统给出的三轴指令姿态角度Ω_c=[α_c; β_c; μ_c]^T。内环为快回路，要求跟踪期望的姿态角速度ω_c，并计算出虚拟控制量——三轴控制力矩M_c。后续设计控制分配模块，将控制力矩合理地分配到执行器中。下面给出姿态终端滑模控制的设计过程。

非线性终端滑模控制具有传统滑模控制的鲁棒性，也能使系统状态在有限时间内收敛，控制精度较高^[21]。在高速飞行器的姿态控制中，其能够取得很好的控制效果^[22-23]。新型终端滑模控制面S设计为式(16)^[17]，

$ S=e+\int_{0}^{t}\left[k_{1} {sig}^{\gamma_{1}}(e)+k_{2} {sig}^{\gamma_{2}}(e)\right] \mathrm{d} \tau, $

(16)

其中：k₁、k₂、γ₁、γ₂为常系数，有k₁>0，k₂>0，γ₁≥1，0 < γ₂ < 1；sig^γ(x)=|x^γ|sgn(x)；e为指令和状态之间的跟踪误差，有e=x-x_c，x_c为期望指令。

设计终端滑模型非线性趋近律为Ṡ=－l₁S－l₂sig^η(S)，其中：l₁、l₂、η为常系数，有l₁>0，l₂>0，0 < η < 1。

外环慢回路滑模控制面设计为${{S_o} = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_c} + \int_0^t {\left[ {{k_1}{{sig }^{{\gamma _1}}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_c}} \right) + {k_2}{{sig }^{{\gamma _2}}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_c}} \right)} \right]} {\rm{d}}\tau } $，则慢回路控制律为

$ \boldsymbol{\omega}_{c}=-g_{o}^{-1}\left[\boldsymbol{f}_{o}-\dot{\boldsymbol{\varOmega}}_{c}+k_{1} {sig}^{\gamma_{1}}\left(\boldsymbol{\varOmega}-\boldsymbol{\varOmega}_{c}\right)+k_{2} {sig}^{\gamma_{2}}\left(\boldsymbol{\varOmega}-\boldsymbol{\varOmega}_{c}\right)+l_{1} S_{o}+l_{2} {sig}^{\eta}\left(S_{o}\right)\right]。$

(17)

同理对于内环快回路，设计滑模面为${{S_o} = \boldsymbol{\omega } - {\boldsymbol{\omega }_c} + \int_0^t {\left[ {{k_1}{{sig }^{{\gamma _1}}}\left( {\boldsymbol{\omega } - {\boldsymbol{\omega }_c}} \right) + {k_2}{{sig }^{{\gamma _2}}}\left( {\boldsymbol{\omega } - {\boldsymbol{\omega }_c}} \right)} \right]} {\rm{d}}\tau } $，系统快回路的控制律为

$ \boldsymbol{M}_{c}=-g_{i}^{-1}\left[f_{i}-\dot{\boldsymbol{\omega}}_{c}+k_{1} {sig}^{\gamma_{1}}\left(\boldsymbol{\omega}-\boldsymbol{\omega}_{c}\right)+k_{2} {sig}^{\gamma_{2}}\left(\boldsymbol{\omega}-\boldsymbol{\omega}_{c}\right)+l_{1} S_{i}+l_{2} {sig}^{\eta}\left(S_{i}\right)\right]。$

(18)

综上，本文设计的高速飞行器再入姿态双环终端滑模控制律见式(17)和式(18)。

3 固定推力器开启数的RCS再分配伪逆法设计

为了简化控制器的设计，本文将姿态控制与控制分配进行模块化设计，控制分配模块的输入是三轴姿态控制指令力矩，合理分配后，输出每个执行器的指令。在RCS系统控制分配算法的设计中，需要综合考虑控制分配方法的分配精度、燃料消耗情况和算法实时性。

根据图 1及表 1对本文研究的RCS系统推力器配置情况分析，可以得到RCS控制分配效率矩阵。

$ \boldsymbol{B}=\left[\begin{array}{l} \ \ \ 0 & \ \ \ 0 & -L_{r} \\ \ \ \ 0 & \ \ \ L_{r} & \ \ \ 0 \\ \ \ \ 0 & \ \ \ 0 & \ \ \ L_{r} \\ \ \ \ 0 & -L_{r} & \ \ \ 0 \\ \ \ \ d & \ \ \ L_{r} \cos \theta_{r} & -L_{r} \sin \theta_{r} \\ -d & \ \ \ L_{r} \cos \theta_{r} & \ \ \ L_{r} \sin \theta_{r} \\ \ \ \ d & -L_{r} \cos \theta_{r} & \ \ \ L_{r} \sin \theta_{r} \\ -d & -L_{r} \cos \theta_{r} & -L_{r} \sin \theta_{r} \end{array}\right]^{\mathrm{T}}。$

(19)

控制分配应该满足两个条件:

1) RCS系统所有推力器燃料消耗总和为最低。由于本文RCS推力器为推力恒定的常值推力器，因此可以用推力器开启总时间来反映燃料消耗量;

2) RCS产生反作用力矩应与控制力矩相等。

则广义逆法的线性规划目标函数表示为$ \min \boldsymbol{f}=\sum\limits_{i=1}^{8} T_{\mathrm{on}i} s . t . \quad \boldsymbol{M}_{\mathrm{RCS}}-\boldsymbol{B} \boldsymbol{u}=0$，其中：M_RCS为计算出的RCS系统指令力矩；u为RCS系统推力矩阵；T_oni为第i个推力器的开启时间。

基于零空间的再分配伪逆法在再分配之前有线性规划的一步，因此是最优的(燃料消耗最少)。但经过再分配之后，已经无法满足最优的条件。且因为伪逆法是基于执行器配置矩阵的，要求各个执行机构都要参与控制，这样就减少了冗余执行器控制分配的灵活性。对于本文研究的8推力器RCS系统来说，控制分配中并不会用到所有的执行器。相反，会因为使用多余的执行器而造成对冲导致燃料的浪费。且由于伪逆法初解时加入了线性规划，实际应用中已经无法保证实时性。

为了保证实时性和降低燃料消耗，针对给定的8推力器RCS配置，本文设计了一种固定推力器开启的再分配伪逆法。固定推力器开启数应与姿态控制系统自由度相同，即为3。因此本文采用固定3推力器开启来设计改进的再分配伪逆法。

设线性规划函数为^[14-15] $ \min \boldsymbol{f}=\boldsymbol{u}^{\mathrm{T}} \boldsymbol{u}, s . t . \quad \boldsymbol{M}_{\mathrm{RCS}}-\boldsymbol{B u}=0$，可获得满足平衡方程的RCS推进器推力为

$ \boldsymbol{u}=\boldsymbol{B}^{\mathrm{T}}\left(\boldsymbol{B} \boldsymbol{B}^{\mathrm{T}}\right)^{-1} \boldsymbol{M}_{\mathrm{RCS}}=\boldsymbol{B}^{+} \boldsymbol{M}_{\mathrm{RCS}}, $

(20)

B⁺=B^T(BB^T)^－1即为控制分配矩阵的广义逆。此时得到了伪逆法的初解(20)。

Step1   由式(20)获得伪逆法初解u_ini=B⁺M_RCS。u_ini一般与一个阈值ε共同使用，ε是一个小整数。当u_ini中的项大于ε时，输出u_p对应项为1，否则u_p为0。

Step2   f_on/off就是根据阈值ε确定u_p中每一项的值的函数。u_p是一个8×1的列矩阵，其中k项为1，8-k项为0，k≥3，即u_p(i₁)=1, 2，…。u_p(i_k)=1，i₁, i₂, …, i_k是可能开启的推力器备选编号。在矩阵(19)控制分配B中找出i₁, i₂, …, i_k对应的列的B(i₁), …, B(i_k)，

$ \boldsymbol{u}_{p(8 \times 1)}=f_{\mathrm{on} / \mathrm{off}}\left(\boldsymbol{B}^{+} \boldsymbol{M}_{\mathrm{RCS}}\right)。$

(21)

Step3   由上文可知，我们选择每个控制指令由3个推力器共同完成。当k=3时，i₁, i₂, …, i_k即为选择的推力器编号，提取出的新配置矩阵B_e=[B(i₁)  B(i₂)  B(i₃)]。当k>3时，将i₁, i₂, …, i_k项和对应的配置矩阵列向量不重复地选择三项进行排列组合，一共有C_k³种排列方法, 备选的推力器开关指令为u_r1, u_r2, …, u_rCk³，以及对应配置矩阵为B_r1, B_r2, …, B_rCk³。

Step4   设计的目标函数为

$ \min \boldsymbol{f}=\sum\left|\boldsymbol{u}_{e}\right| {\ s. t\ } \boldsymbol{M}_{\mathrm{RCS}}-\boldsymbol{B}_{e} \boldsymbol{u}_{e}=0, $

(22)

其中：u_e∈{u_r1 … u_rCk³}；B_e∈{B_r1 … B_rCk³}。

求解式(22)即可获得3推力器开启下的最少燃料消耗的各推力器的指令推力。由于已经给定了u_e和B_e的范围，若有推力器出现失效故障，则可以在推力器配置矩阵(19)中，将对应损坏推力器的列向量去除掉，并将剩余列向量组成新控制分配矩阵B_ini带入step1即可。

4 数值仿真

本文研究的飞行器模型的机翼参考面积为3.35 m²，平均气动弦长为2.44 m，机翼展长为1.83 m，机身质量为1 259 kg，三轴惯性矩为I_xx=156 kg·m², I_yy=1 162 kg·m², I_zz=1 267 kg·m²。

系统姿态变量初值为[ω_x, ω_y, ω_z, α, β, μ]=[0, 0, 0, 2.5°, 0.3°, 0.2°]。期望姿态为攻角2°，期望侧滑角和速度滚转为0°。对不加分配的理想情况下终端滑模控制算法，零空间再分配伪逆法(null space pseudo-inverse, NPI)和本文设计的3推力器开启再分配伪逆法(pseudo-inverse, PI)进行无故障状态的对比仿真，结果如下。

定义跟踪轨迹的误差为$ error=\int\limits_{t_{0}}^{t_{f}}\left|y-r^{*}\right| \mathrm{d} t /\left(t_{f}-t_{0}\right)$。则不同分配方法的姿态跟踪误差见表 2。

同时也在其他姿态跟踪指令下进行了多组实验，来确定比较两种方法的推力器开启总时间。见表 3。

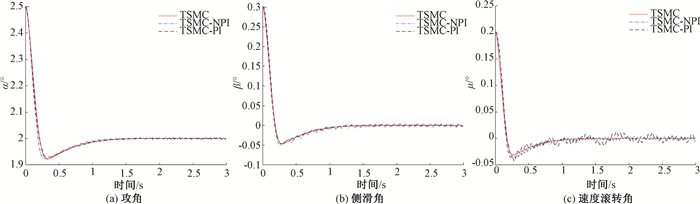
从图 3和表 2中的图像和跟踪误差值可以看出，本文设计的固定3推力器开启的改进再分配伪逆法和基于零空间的再分配伪逆法都能取得比较好的控制效果，两种方法的跟踪误差都很小。由表 3看出在三种期望姿态角度的条件下，本文设计的固定3推力器开启的改进再分配伪逆法均有更短的推力器开启时间。也就是说明，本文设计的固定3推力器开启的改进再分配伪逆法能让RCS有更低的燃料消耗。

5 结论

根据RCS系统对高实时性和低燃料消耗的要求，本文设计了一种固定推力器开启数的改进再分配伪逆法的控制分配系统，并应用在了高速飞行器再入段RCS系统姿态控制中。本文建立了高速飞行器六自由度模型，对RCS系统配置进行了分析和建模。设计了基于有限时间终端滑模算法的姿态控制系统。针对给定8推力器配置的RCS系统，设计了固定3推力器开启的改进再分配伪逆控制分配算法，通过在给定的小范围内进行线性规划，大大减少了运算量，提高了控制分配系统的实时性。由数值仿真结果能够看出，本文设计的固定推力器开启数的再分配伪逆控制系统，在提高实时性的基础上具有良好的控制效果和更低的燃料消耗。