传统网络中的节点在通信之前必须先找到一条端到端的通信链路,再完成数据包的转发任务,这意味着传统网络拓扑在大多数时间内是连通的,并且源节点和目的节点之间至少存在一条连通链路。在某些实际应用场景下,源、目的节点对之间通常不存在端到端的多跳链路,导致传统网络的路由策略无法有效运行。为了解决特殊环境下的通信问题,机会网络受到科研人员的广泛关注。机会网络利用节点移动过程中形成的相遇机会,采用“存储-携带-转发”的方式进行数据传输[1-2],对节点随机移动、分布密度不定、有限的通信范围等特性,具有较强的适应性。因此机会网络在车载设备所形成的车载网、野生动物信息收集、大型集会(如大型体育赛事现场、演唱会等)、偏远地区以及深空通信等领域具有广泛的应用前景。
机会网络的网络拓扑频繁变化且链路持续时间不确定,所以网络被划分成若干个不连通的子区域,又可称为“间歇性连接网络”[3]。在这样的网络环境中进行数据传输不能事先确定转发路径,需要采用边路由边传输的方式选择每一跳节点。数据包在经历多跳后,传送至目的地。路由决策问题一直是机会网络的研究重点,其实质是如何选择合适的中继节点协助完成数据传送任务。到目前为止,机会网络中的路由协议按照选择中继的方式可以分为两类:一类是零信息型路由,不需要依赖复杂的网络信息,仅利用节点移动产生的相遇机会完成数据传输;另一类是信息辅助型路由,需要依靠额外的信息才能做出转发决策,即根据节点信息计算节点的效用值,进一步选择高效用节点路由数据包,又称为效用路由。
零信息型路由没有考虑网络中节点的异质性,采用较为单一的路由方式完成数据包的交换和传递。信息辅助型路由是当前路由工作研究的重点,评估函数根据不同类型的参数信息对节点路由数据包的能力进行判断。这些信息可以分为节点的历史接触信息[4-6]、节点的社会性信息[7-11]、节点的位置信息[12-15]、节点能量信息[16-18]等。机会网络中的许多路由协议是互有交叉和联系的[9-10, 14],最终目的是针对不同的网络环境,综合节点的多方面信息,衡量节点的转发能力以提高网络性能。为进一步提高网络的投递率和传输速度,在信息辅助型路由的基础上,研究人员提出了效用和冗余混合的路由方案,但该方案可能存在较高的网络开销。此外,数据包始终朝着高效用节点方向传输会造成高效用节点的能量过多消耗。特别是在能量有限的情况下,一旦高效用节点的能量消耗殆尽,将加剧网络间歇性,使得网络性能急剧下降。考虑到依靠节点的社会属性信息选择中继已经被证明可以取得较好的路由性能,本文利用节点的社会效用指导路由,进一步降低网络开销,均衡节点在数据传输过程中的能量消耗,以避免高效用节点能量消耗过快。
基于上述分析,本文提出了一种基于节点效用和能量(probability and energy, ProEnergy)的多副本路由算法,在保证较优网络性能的前提下充分利用节点的效用降低网络开销和均衡节点的能量消耗。
1 算法设计思路 1.1 路由设计思路机会网络中的节点大多由人携带的智能终端构成,其表现出的社会活动可能遵循某些社会特征[19]。不同的路由协议利用节点的中心性、相似性、社区属性等不同的社会度量来选择合适的中继节点[20-22]。在以往的基于社会属性的路由工作中,忽略了节点关系的自身差异性和动态变化性对路由数据包的影响,所以本文提出新的效用指标衡量节点的社会关系。为避免多备份路由中出现过高网络开销的问题,该路由算法研究如何充分利用节点关系进一步降低网络开销。此外,为防止网络中高效用节点因过多的数据传输导致能量过快耗尽而加重网络的间歇性,在数据转发过程中,利用节点的社会效用和剩余能量共同判断节点的转发能力,以实现均衡节点能量的目的。
本文提出的路由算法的设计思路如图 1所示,首先构建网络模型,维护节点的接触信息和信息更新机制,为数据转发工作提供充分的准备;其次,设计了基于节点效用和能量的路由方案,主要包括识别亲密节点、构建关系模型、路由决策三大步骤。
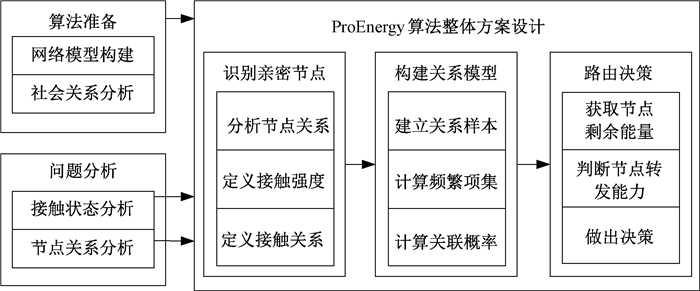
|
图 1 ProEnergy算法整体方案设计 Fig. 1 Overall scheme design of ProEnergy algorithm |
本文利用具有时间属性的接触图Gt (V, E)构建具有社会特征的网络模型。假设网络中有n个节点,V={v1, v2, …, vn}表示节点集合,tx表示时间,相关定义如下。
定义1 邻居节点集合。网络中任意两节点vi和vj的距离小于某个阈值d,则两节点互为彼此的邻居节点。节点vi在tx时刻下的邻居节点集合为Nb(vi),表示为
| $ N b\left(v_{i}\right)=\left\{v_{j} \mid D\left(v_{i}, v_{j}\right)<d\right\}, $ | (1) |
其中:D(vi, vj)为节点vi和vj的通信距离;d为两节点可通信的最大距离。
定义2 接触信息。节点vi和节点vj的累计接触时长定义为CTvitx(vj),节点vi和节点vj的累计断开时长定义为OTvitx(vj)。
网络的总时长用T={t0, t1, …, tm}表示,其中T被均匀划分为m个不同的时刻,相邻t之间的时间间隙均为Δt。δΔtx(vi, vj)表示节点vi与vj在第x个Δt时隙的接触情况:
| $ \delta_{\Delta t}^{x}\left(v_{i}, v_{j}\right)= \begin{cases}1, & v_{j} \in N b\left(v_{i}\right), \\ 0, & v_{j} \notin N b\left(v_{i}\right),\end{cases} $ | (2) |
当δΔtx(vi, vj)=1时,说明节点vi与vj在彼此的通信范围内,可相互发送数据包。节点vi和vj的累计接触时长CTvitx(vj)和累计断开时长OTvitx(vj)根据节点接触状态自动更新,即
| $ \begin{cases}C T_{v_{i}}^{t_{x}}\left(v_{j}\right)=C T_{v_{i}}^{t_{x-1}}\left(v_{j}\right)+\Delta t, & \delta_{\Delta t}^{t_{x}}\left(v_{i}, v_{j}\right)=1, \\ O T_{v_{i}}^{t_{x}}\left(v_{j}\right)=O T_{v_{i}}^{t_{x-1}}\left(v_{j}\right)+\Delta t, & \delta_{\Delta t}^{t_{x}}\left(v_{i}, v_{j}\right)=0 。\end{cases} $ | (3) |
定义3 节点的接触强度。在tx时刻,节点vi和vj的接触强度定义为两节点接触时长与断开时长之比。
| $ C S_{v_{i}}^{t_{x}}\left(v_{j}\right)=\frac{C T_{v_{i}}^{t_{x}}\left(v_{j}\right)}{O T_{v_{i}}^{t_{x}}\left(v_{j}\right)}。$ | (4) |
两节点的接触强度越大,说明两节点建立联系的机会就越大。由于两节点接触、断开具有相互性,因此CSvitx(vj)=CSvjtx(vi)。
定义4 平均接触强度。节点vi在tx时刻下的平均接触强度表示为当前与历史通信节点的接触强度总和的平均,代表节点vi在网络tx时刻下接触的平均水平。
| $ A C S_{v_{i}}^{t_{x}}=\frac{1}{\left|N\left(v_{i}\right)\right|} \sum\limits_{v_{j} \in N\left(v_{i}\right)} C S_{v_{i}}^{t_{x}}\left(v_{j}\right), $ | (5) |
其中:N(vi)和|N(vi)|分别表示节点vi的历史接触的邻居节点集和历史接触邻居节点个数。N(vi)根据节点vi在tx时刻下的接触情况进行更新。
| $ N\left(v_{i}\right)=N\left(v_{i}\right)_{\text {old }} \cup\left\{v_{j} \mid D\left(v_{i}, v_{j}\right)<d, v_{j} \notin N\left(v_{i}\right)_{\text {old }}\right\}, $ | (6) |
N(vi)old表示节点vi在tx-1时刻下历史邻居节点集。所以节点的历史邻居节点集由前一时刻的历史邻居节点集与当前时刻新加入的邻居节点构成。
定义5 接触关系。若CSvitx(vj)>ACSvitx,表示在tx时刻下节点vi和节点vj存在强接触关系。反之,CSvitx(vj)<ACSvitx,节点vi和节点vj为弱接触关系。
2 关系模型 2.1 预测接触强度基于全局的时间可以较好地对比不同节点间接触强度,但并不能较好地反映单对节点间接触强度的瞬时变化。因此,挖掘单个节点对在短时间内接触强度的变化规律,预测两节点未来的接触强度,可更加有针对性地指导路由完成工作。本文采用GM(1, 1)预测模型,该模型是一种小样本预测模型,可以利用少量的历史数据预测下一时刻的数据,对不确定性情况有较好的预测效果[23-25]。假设某节点对在当前时刻tx下是接触状态,而在未来的tx+1时刻其接触状态不确定,且与节点在过去tx-1、tx-2、…、tx-n时刻的接触或断开状态并无关联。节点运动在长时间下呈现突变性和不规律性,随着网络时间的增加,两节点在tx-n与tx+n时刻下的接触强度可能会发生较大变化。而节点在短时间内的接触强度变化浮动较小,可能呈现出某种规律性。因此,可以利用这种变化规律,对未来短时间内节点的接触强度进行预测。
GM(1, 1)的接触强度预测过程如下。
1) 获取当前时刻tx与其历史w-1个时刻节点的接触强度,共计w个时刻的接触强度,由此给出原始的接触强度序列,
| $ C S_{v_{i}, v_{j}}^{(0)}=\left\{C S_{v_{i}, v_{j}}^{(0)}(1), C S_{v_{i}, v_{j}}^{(0)}(2), \cdots, C S_{v_{i}, v_{j}}^{(0)}(w)\right\}。$ | (7) |
2) 把原始接触强度序列做累加,生成CSvi, vj(1)序列,称CSvi, vj(1)为CSvi, vj(0)的1-AGO序列。
| $ C S_{v_{i}, v_{j}}^{(1)}=\left\{C S_{v_{i}, v_{j}}^{(1)}(1), C S_{v_{i}, v_{j}}^{(1)}(2), \cdots, C S_{v_{i}, v_{j}}^{(1)}(w)\right\}, $ | (8) |
其中:CSvi, vj(1)(k)=CSvi, vj(1)(1)+CSvi, vj(1)(2)+…+CSvi, vj(1)(k),对累加序列CSvi, vj(1)进行紧邻均值处理,生成新的序列Zvi, vj(1),
| $ Z_{v_{i}, v_{j}}^{(1)}=\left\{Z_{v_{i}, v_{j}}^{(1)}(2), Z_{v_{i}, v_{j}}^{(1)}(3), \cdots, Z_{v_{i}, v_{j}}^{(1)}(w)\right\}, $ | (9) |
Zvi, vj(1)称为背景值,
3) 对累加后的接触强度序列建立GM(1, 1)模型的一阶微分方程,其相应的白化微分方程为
| $ \frac{\mathrm{d} C S_{v_{i}, v_{j}}^{(1)}}{\mathrm{d} t}+a C S_{v_{i}, v_{j}}^{(1)}(t)=b, $ | (10) |
其中:a称作发展系数;b称作灰色作用量,均为常数。采用最小二乘法求得a、b的值,满足等式
| $ [a, b]^{\mathrm{T}}=\left(\boldsymbol{B}^{\mathrm{T}} \boldsymbol{B}\right)^{-1} \boldsymbol{B}^{\mathrm{T}} Y, $ | (11) |
其中:
| $ \boldsymbol{Y}=\left[\begin{array}{c} C S_{v_{i}, v_{j}}^{(0)}(2) \\ C S_{v_{i}, v_{j}}^{(0)}(3) \\ \vdots \\ C S_{v_{i}, v_{j}}^{(0)}(w) \end{array}\right] ; \boldsymbol{B}=\left[\begin{array}{cc} -Z_{v_{i}, v_{j}}^{(1)}(2) & 1 \\ -Z_{v_{i}, v_{j}}^{(1)}(3) & 1 \\ \vdots & \vdots \\ -Z_{v_{i}, v_{j}}^{(1)}(w) & 1 \end{array}\right] \text { 。} $ | (12) |
4) 将矩阵展开得到参数a、b的表达式:
| $ a=\frac{\sum\limits_{k=2}^{n} C S_{v_{i}, v_{j}}^{(0)}(k) \sum\limits_{k=2}^{n} Z_{v_{i}, v_{j}}^{(1)}(k)-(w-1) \sum\limits_{k=2}^{n} C S_{v_{i}, v_{j}}^{(0)}(k) Z_{v_{i}, v_{j}}^{(1)}(k)}{(w-1) \sum\limits_{k=2}^{n}\left(Z_{v_{i}, v_{j}}^{(1)}(k)\right)^{2}-\left(\sum\limits_{k=2}^{n} Z_{v_{i}, v_{j}}^{(1)}(k)\right)^{2}}; $ | (13) |
| $ b=\frac{\sum\limits_{k=2}^{n} C S_{v_{i}, v_{j}}^{(0)}(k) \sum\limits_{k=2}^{n}\left(Z_{v_{i}, v_{j}}^{(1)}(k)\right)^{2}-\sum\limits_{k=2}^{n} Z_{v_{i}, v_{j}}^{(1)}(k) \sum\limits_{k=2}^{n} Z_{v_{i}, v_{j}}^{(1)}(k) C S_{v_{i}, v_{j}}^{(0)}(k)}{(w-1) \sum\limits_{k=2}^{n}\left(Z_{v_{i}, v_{j}}^{(1)}(k)\right)^{2}-\left(\sum\limits_{k=2}^{n} Z_{v_{i}, v_{j}}^{(1)}(k)\right)^{2}}。$ | (14) |
5) 求解微分方程,得到GM(1, 1)模型的离散解,
| $ C S_{v_{i}, v_{j}}^{(1)}(k+1)=\left(C S_{v_{i}, v_{j}}^{(0)}(1)-\frac{b}{a}\right) \mathrm{e}^{-a k}+\frac{b}{a} 。$ | (15) |
6) 还原为原始数列,预测模型为
| $ C S_{v_{i}, v_{j}}^{(0)}(k+1)=C S_{v_{i}, v_{j}}^{(1)}(k+1)-C S_{v_{i}, v_{j}}^{(1)}(k), $ | (16) |
将式(15)代入得
接触强度的预测方法充分考虑节点的运动特性,以节点在较短时间内的运动规律为基础,挖掘节点间的接触强度随时间推移的动态特征,更适用于预测在未来短时间内节点间的接触强度。
2.2 构建关系样本节点依靠社会环境生存,而不是独立个体,每个节点都会存在相对亲密的社会关系。节点与其存在亲密关系的节点可能会存在较多的接触机会,所以我们认为节点与存在强接触关系的节点存在相对亲密的社会关系。为了进一步分析节点关系,以帮助减少网络开销,首先利用节点接触关系来建立节点关系矩阵。
定义6 关系矩阵。根据节点的平均接触强度维护一个n×n的关系矩阵R,
| $ \boldsymbol{R}=\left(\begin{array}{cccc} r_{1}^{t_{x}} & r_{2 \rightarrow 1} & \cdots & r_{n \rightarrow 1} \\ r_{1 \rightarrow 2} & r_{2}^{t_{x}} & \cdots & r_{n \rightarrow 2} \\ \vdots & & r_{j}^{t_{x}} & \vdots \\ r_{n \rightarrow 1} & r_{n \rightarrow 2} & \cdots & r_{n}^{t_{x}} \end{array}\right) 。$ | (17) |
矩阵R对角线位置为ritx,ritx表示在tx时刻依据预测的接触强度计算得到节点vi的平均接触强度ACSvitx。第i行、第j列的交叉位置表示节点vj与节点vi的接触关系rj→i,其取值为
| $ r_{j \rightarrow i}= \begin{cases}1, & C S_{v_{i}}^{t_{x}}\left(v_{j}\right)>A C S_{v_{i}}^{t_{x}} ;\\ 0, & C S_{v_{i}}^{t_{x}}\left(v_{j}\right)<A C S_{v_{i}}^{t_{x}};\end{cases} $ | (18) |
其中:CSvitx(vj)是在tx时刻预测出的节点vi与节点vj的接触强度。当rj→i=1时,表示节点vj与节点vi存在某种亲密关系;当rj→i=0时,表示节点vj与节点vi不存在亲密关系。需要注意的是,关系矩阵R为非对称矩阵,ri→j≠rj→i,ri→j取值依据为ACSvjtx,即:
| $ r_{i \rightarrow j}= \begin{cases}1, & C S_{v_{j}}^{t_{x}}\left(v_{i}\right)>A C S_{v_{j}}^{t_{x}}, \\ 0, & C S_{v_{j}}^{t_{x}}\left(v_{i}\right)<A C S_{v_{j}}^{t_{x}} 。\end{cases} $ | (19) |
Apriori算法由Agrawal于1994年提出,该算法是经典的挖掘数据关联规则的算法[26-27]。图 2给出了该模型的工作流程,主要分为两大步骤:第一步是发现频繁项集,目的是从数据集中找出频繁出现的项集;第二步是发现关联规则,即在频繁项集中利用条件概率求出关联规则,利用潜在规律进行预测。Scan称为数据集选择过程,主要作用在于支持度过滤,删除不满足最小支持度的项集,保留满足最小支持度的项集。
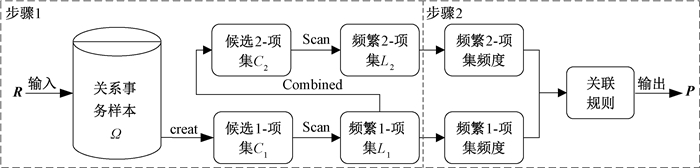
|
图 2 基于Apriori算法的关系挖掘模型 Fig. 2 Relationship mining model based on Apriori algorithm |
针对本文提出的网络环境,结合Apriori算法建立关系模型,节点的关系矩阵R作为模型输入,最终获得节点的社会转发效用,帮助路由做出转发决策。模型根据输入的关系矩阵R,将每个节点存在的亲密关系保存在关系事务样本Ω相应的记录中。候选项集C1、C2和频繁项集L1、L2中的每个元素都是一个集合,且集合中元素为网络中的节点。C1、L1中每个元素称为1-项集,C2、L2中每个元素称为2-项集。1-项集和2-项集又统一称为项集。
由图 2可知,根据Ω产生候选1-项集,则C1={{v1}, {v2}, …, {vn}},其包含事务样本中所有的节点项,即共包含n个1-项集。Scan过程的最初阶段为计算项集频度,该阶段是以候选项集C为基础进行计算。假设项集用I表示,在网络当前时间tx下,项集I的频度定义为
| $ F r e_{I}^{t_{x}}=\partial^{t_{x}}(I), $ | (20) |
| $ \partial^{t_{x}}(I)=\sum\limits_{k=1}^{n} F(I, k), $ | (21) |
其中:F(I,k)表示网络中第k个节点和项集I中所包含节点的关系函数。项集I又分为1-项集I1和2-项集I2。当I=I1,计算1-项集频度,最终获得该节点在tx下存在亲密关系的数量。假设I1={vi},其中vi为网络中的第i个节点,则函数F(I, k)=F(I1, k)且k≠i, 其取值情况为
| $ F\left(I_{1}, k\right)= \begin{cases}1, & \boldsymbol{R}[k][i]=1 ,\\ 0, & \boldsymbol{R}[k][i]=0,\end{cases} $ | (22) |
当I=I2,计算2-项集频度,最终获得项集中两节点在tx时刻下存在共同亲密节点的数量。假设I2={vi, vj},则函数F(I, k)=F(I2, k)且k≠i或k≠j, 其取值情况为
| $ F\left(I_{2}, k\right)=\left\{\begin{array}{c} 1, &\boldsymbol{R}[k][i]=1, \boldsymbol{R}[k][j]=1, \\ 0,&\text { 其他。} \end{array}\right. $ | (23) |
Scan过程的最初阶段最终获得所有候选项集的频度。第二阶段依据最小支持度TM获得频繁集L。在当前时间tx下,根据候选集C中项集I的频度FreItx与最小支持度TM的关系得到频繁集L,所用公式为
| $ \left\{\begin{array}{l} I \in L^{t_{x}}, \quad F r e_{I}^{t_{x}}>T_{M}, \\ I \notin L^{t_{x}}, \quad F r e_{I}^{t_{x}}<T_{M}, \end{array}\right. $ | (24) |
Ltx包括L1tx和L2tx,表示频繁1-项集和频繁2-项集。频繁1-项集中包含的节点称为网络中的活跃节点,频繁2-项集中包含的对应两节点称为网络中的频繁接触节点对。
Apriori模型的第二步,需要进一步计算节点可通过共同亲密节点建立联系的概率。假设在tx时刻下,2-项集{vi, vj}∈L2tx,现需要计算节点vi与vj能够通过潜在关系建立联系的概率。用p(vi⇒vj)tx表示在tx时刻下节点vi通过潜在关系与节点vj建立联系的概率。其公式定义为
| $ p_{\left(v_{i} \Rightarrow v_{j}\right)}^{t_{x}}=\frac{N u m^{t_{x}}\left(v_{i} \cup v_{j}\right)}{{Num}^{t_{x}}\left(v_{i}\right)}=\frac{F r e_{\left\{v_{i}, v_{j}\right\}}^{t_{x}}}{F r e_{\left\{v_{i}\right\}}^{t_{x}}}, $ | (25) |
其中:Fre{vi, vj}tx表示L2tx中2-项集{vi, vj} 的频度;项集Fre{vi}tx表示L1tx中1-项集{vi}的频度;Numtx(vi∪vj) 表示事务样本中同时包含节点vi和节点vj的事务数量;Numtx(vi)表示事务样本包含节点vi的事务数量;p(vi⇒vj)tx表示tx时刻下包含节点vi的事务中出现节点vj的条件概率,该概率表示节点vi与节点vj通过潜在关系建立联系的可能性,又可称为节点vi能够将数据包转发给节点vj的社会转发效用。值得注意的是,根据关系模型,在tx时刻下,节点vj能够将数据包转发给节点vi的社会转发效用p(vj⇒vi)tx与节点vi能够将数据包转发给节点vj的社会转发效用p(vi⇒vj)tx并不相等,计算公式为
| $ p_{\left(v_{j} \Rightarrow v_{i}\right)}^{t_{x}}=\frac{N u m^{t_{x}}\left(v_{i} \cup v_{j}\right)}{{Num}^{t_{x}}\left(v_{j}\right)}=\frac{F r e_{\left\{v_{i}, v_{j}\right\}}^{t_{x}}}{F r e_{\left\{v_{j}\right\}}^{t_{x}}}, $ | (26) |
即包含节点vj的事务中出现节点vi的条件概率作为节点vj能够将数据包转发给节点vi的转发效用。当2-项集{vi, vj}∉L2tx时,则p(vj⇒vi)tx=0,认为节点vi与vj建立潜在关联的概率较小,可忽略不计。
3 ProEnergy路由方案 3.1 能量权重因子在ProEnergy路由方案中将节点能量的初始值设置为500,假设节点在接收和转发数据包时均会消耗1个单位的能量。根据节点的剩余能量来决定是否参与数据的转发,当节点的能量小于某个阈值时,其只接收需要传送到该节点的数据包。只有当节点的能量大于该阈值时,则需综合节点的社会转发效用和剩余能量共同计算节点的转发能力,
| $ P\left(v_{i}, v_{j}\right)=\lambda \times p_{\left(v_{i} \Rightarrow v_{j}\right)}^{t_{x}}+(1-\lambda) \times C_{i}, $ | (27) |
其中:λ (λ∈[0, 1])为权重因子;p(vi⇒vj)tx为vi到vj的社会转发效用,且p(vi⇒vj)tx<1;Ci为节点vi的剩余能量。为了消除指标之间的量纲影响,采用离差标准化对节点vi的剩余能量Ci进行标准化处理,
| $ C_{i}=\frac{C_{i}-C_{\min }}{C_{\max }-C_{\min }}, $ | (28) |
其中:Cmin表示网络中节点能量剩余的最小值;Cmax表示网络中节点剩余能量的最大值。在对能量进行标准化处理后,依据节点的剩余能量和社会效用共同计算中间节点的转发能力,并指导路由工作的完成。为了较好地平衡网络性能和资源消耗问题,权重因子λ的取值会在实验部分给以详细说明。
3.2 ProEnergy路由算法本文提出的ProEnergy路由算法主要步骤如下。
输入:M是数据包,dM是M的目的节点,tx是网络运行的当前时刻,GM(1, 1)保存了tx-5到tx-1时刻下节点间接触强度
输出:M是否转发
1) for 任意节点a、b、dM∈V do
2) if a和b相互通信且M由a携带 then
3) 基于CTatx(b)和OTatx(b),计算CSatx(b), 更新GM(1, 1)
4) if b没有携带M的副本 then
5) if a和b的能量大于50 then
6) if b是M的目的节点 then
7) 更新包信息, a转发M给b
8) else
9) 计算CSatx(dM)和CSbtx(dM), 更新GM(1, 1),计算CSatx(dM), CSbtx(dM), CSatx(b), ACSa, ACSb, ACSdM, 更新R
10) 基于R计算L1和L2, 计算p(a⇒dM)tx和p(b⇒dM)tx, 归一化Ca和Cb, 计算P(a, dM)和P(b, dM)
11) if P(a, dM)<P(b, dM) then
12) 更新包信息, a转发M副本给b
13) end if
14) end if
15) end if
16) end if
17) end if
18) end for
4 仿真实验 4.1 仿真环境与参数设置为了性能评估,本文实验基于移动机会网络模拟器平台[28]。节点的移动轨迹使用RealTrace-KAIST数据集[29],其他的仿真参数如表 1所示。利用Apriori算法计算关联概率时,最小支持度TM设置为45。本文使用数据包的投递率、传输时延、网络开销、总能量消耗、能量消耗标准差5个指标来评价路由算法的性能,并与Prophet算法、PageRank算法、GeoSocial算法进行对比。
|
|
表 1 实验参数设置 Tab. 1 Setting of experimental parameters |
首先分析λ对网络性能的影响。图 3(a)给出了λ取值范围在0.5~0.8下的投递率情况,观察可知4种情况下的投递率走势相似,从λ=0.8到λ=0.5的投递率依次下降,是因为节点的社会效用影响逐渐减小。ProEnergy采用多副本的路由方式,所以在不同λ取值下均获得较高的传递概率。图 3(b)给出了传输延时情况,观察可知λ =0.7时其传输时延最低;当λ =0.5时其传输时延较高,是由于当λ值较小时,因数据包被较多传送到能量相对较高、但关联概率较低的节点上,从而导致时延增大。图 3(c)给出了网络开销情况,观察可知取λ =0.5~0.8,节点的网络开销依次减小。当λ增大,那些关联概率较小,但能量较高节点携带数据包的机会就越小,所以造成网络副本数有所降低。通过综合的对比分析,当λ=0.7时,路由可以获得最优的网络性能。
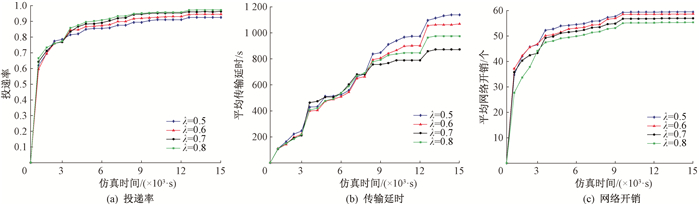
|
图 3 不同λ下的实验结果 Fig. 3 Experimental results with different λ |
图 4(a)给出网络中90个节点的总能量消耗情况。可以看出4个算法的能量消耗随仿真时间的运行而增加。仿真时间在3 200 s之前,ProEnergy算法总能量消耗大于Prophet算法,是由于仿真初期节点的接触次数有限,Prophet算法只计算通信范围内节点的效用。而ProEnergy算法是根据历史通信记录计算节点的社会效用,由于在网络初期节点间的接触情况不稳定,且节点能量充足,使较多的节点参与数据转发工作,而造成较高的能量消耗。但随着实验进行,ProEnergy算法消耗的总能量趋于稳定,而Prophet算法却不断增加。仿真结束时,PageRank算法的能量消耗达到35 000 J左右,是路由算法中消耗最高的。GeoSocial算法的能量消耗达到34 000 J左右,Prophet算法消耗达到29 000 J左右,而ProEnergy算法为21 000 J左右。
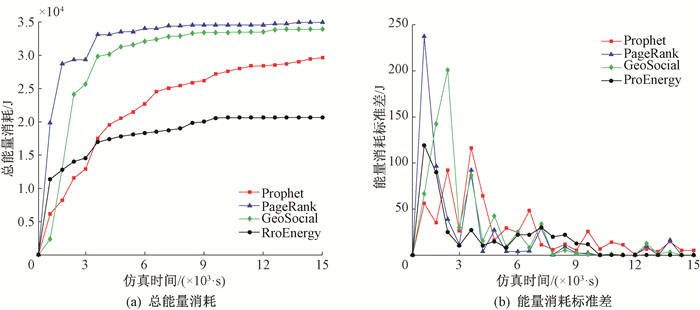
|
图 4 能量实验结果 Fig. 4 Energy experiment results |
图 4(b)给出了节点能量消耗标准差随仿真时间增加的变化情况。每隔600 s就对90个节点的剩余能量进行一次输出,再经计算最终得出90个节点在每600 s内能量消耗的标准差。从图 4中可以看出,所有算法在仿真初期(0~3 000 s),标准差的起伏变化较大,这是因为消息在网络中分布不均匀造成的,3 000 s后可以明显看到ProEnergy算法的标准差小于其他3种路由算法,说明ProEnergy算法能够均衡节点的能量消耗,在数据传输时不过度利用某一个节点进行数据转发,避免某些高效用节点因能量耗尽过早死亡。
4种算法的投递率如图 5(a)所示,4种算法均以多副本的方式完成路由工作,所以都获得较高的投递率。可以看出,仿真实验在7 000 s之前PageRank算法明显高于其他三种算法。当仿真实验结束时,PageRank最终投递率为0.98,GeoSocial为0.97,ProEnergy为0.96,三者投递率接近,Prophet算法投递率较低,为0.89。当高效用节点能量不充足的时,ProEnergy算法让社会关系较小且能量充足的节点也能够优先发送消息,相比Prophet算法,在相遇时根据接触信息更新节点效用获得了更好性能,避免数据包在节点缓冲区中过久存储而造成包丢弃的情况出现。
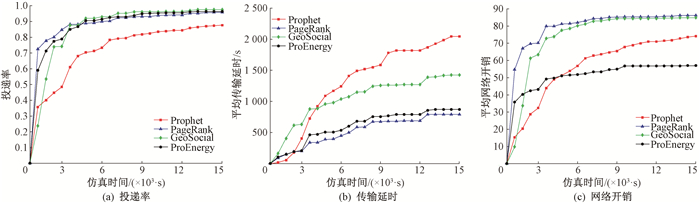
|
图 5 网络性能实验结果 Fig. 5 Experimental results of network performance |
4种算法的平均传输延时如图 5(b)所示,可以看出随着仿真时间的增加,算法的传输延时增大。在仿真初期(0~3 200 s),GeoSocial算法的传输延时最大,但之后,Prophet算法随着仿真时间的增加,传输延时不断增大,是由于Prophet算法在节点接触时更新节点效用,且由高效用节点携带数据包,没有考虑节点的能量问题,将节点传递给高效用节点后,高效用节点可能因过多能量消耗,加重网络间歇性,导致较高的传输延时。在仿真结束时,Prophet的时延最大,大约为2 050 s,GeoSocial大约为1 400 s,而ProEnergy略高于PageRank,PageRank大约为800 s,ProEnergy大约为870 s。ProEnergy算法相比Prophet和GeoSocial算法可以有效避免因关键节点能量过早耗尽而减小传输时延。
4种算法的平均网络开销如图 5(c)所示。平均网络开销表示网络中产生的所有数据包副本数与数据包总数的比值。仿真实验在3 200 s之前,ProEnergy算法网络开销大于Prophet算法,但之后ProEnergy算法网络开销逐渐平稳,其原因与能量类似。实验结束时,PageRank、GeoSocial、Prophet算法的副本数高于ProEnergy。
5 总结本文提出了一种基于效用和能量的机会路由算法。首先,对节点关系进行分析,构建网络模型,引入Apriori算法建立关系模型,计算节点的社会转发效用。其次,添加能量因子以均衡节点的能量消耗,优化路由性能。最后,对提出的算法进行仿真。实验结果表明,在保证较高投递率和较低平均延时的同时,有效降低了网络开销,并均衡了节点的能量消耗,为今后多备份路由算法的研究提供了参考。
| [1] |
WU D P, ZHANG F, WANG H G, et al. Security-oriented opportunistic data forwarding in mobile social networks[J]. Future generation computer systems, 2018, 87: 803-815. DOI:10.1016/j.future.2017.07.028 (  0) 0) |
| [2] |
刘尚坤, 魏功, 何欣. 一种基于分簇的机会网络路由算法[J]. 郑州大学学报(理学版), 2014, 46(3): 49-53. LIU S K, WEI G, HE X. Cluster-based opportunistic network data delivery algorithm[J]. Journal of Zhengzhou university (natural science edition), 2014, 46(3): 49-53. (  0) 0) |
| [3] |
YUAN P Y, FAN L L, LIU P, et al. Recent progress in routing protocols of mobile opportunistic networks: a clear taxonomy, analysis and evaluation[J]. Journal of network and computer applications, 2016, 62: 163-170. DOI:10.1016/j.jnca.2016.01.006 (  0) 0) |
| [4] |
PATEL D, SHAH R. Improved PROPHET routing protocol in DTN[J]. International research journal of engineering technology, 2016, 3(6): 503-509. (  0) 0) |
| [5] |
HUI P, CHAINTREAU A, SCOTT J, et al. Pocket switched networks and human mobility in conference environments[C]//Proceeding of the 2005 ACM SIGCOMM Workshop on Delay-tolerant Networking. Pennsylvania: ACM Press, 2005: 244-251.
(  0) 0) |
| [6] |
WANG X M, LIN Y G, ZHANG S S, et al. A social activity and physical contact-based routing algorithm in mobile opportunistic networks for emergency response to sudden disasters[J]. Enterprise information systems, 2017, 11(5): 597-626. DOI:10.1080/17517575.2015.1067840 (  0) 0) |
| [7] |
BRIN S, PAGE L. The anatomy of a large-scale hypertextual Web search engine[J]. Computer networks and ISDN systems, 1998, 30(1/2/3/4/5/6/7): 107-117. (  0) 0) |
| [8] |
AL AYYAT S, HARRAS K A, ALY S G. Interest aware PeopleRank: Towards effective social-based opportunistic advertising[C]//2013 IEEE Wireless Communications and Networking Conference. Shanghai: IEEE Press, 2013: 4428-4433.
(  0) 0) |
| [9] |
HUI P, CROWCROFT J, YONEKI E. BUBBLE rap: social-based forwarding in delay-tolerant networks[J]. IEEE transactions on mobile computing, 2011, 10(11): 1576-1589. DOI:10.1109/TMC.2010.246 (  0) 0) |
| [10] |
QIRTAS M M, FAHEEM Y, REHMANI M H. A cooperative mobile throwbox-based routing protocol for social-aware delay tolerant networks[J]. Wireless networks, 2020, 26(6): 3997-4009. DOI:10.1007/s11276-020-02288-1 (  0) 0) |
| [11] |
BOLDRINI C, CONTI M, JACOPINI J, et al. HiBOp: a history based routing protocol for opportunistic networks[C]//2007 IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks. Espoo: IEEE Press, 2007: 1-12.
(  0) 0) |
| [12] |
LINDGREN A, DORIA A, SCHELÉN O. Probabilistic routing in intermittently connected networks[J]. ACM SIGMOBILE mobile computing and communications review, 2003, 7(3): 19-20. DOI:10.1145/961268.961272 (  0) 0) |
| [13] |
DHURANDHER S K, BORAH S, WOUNGANG I, et al. EDR: an encounter and distance based routing protocol for opportunistic networks[C]//2016 IEEE 30th International Conference on Advanced Information Networking and Applications. Crans-Montana: IEEE Press, 2016: 297-302.
(  0) 0) |
| [14] |
SHARMA D K, DHURANDHER S K, WOUNGANG I, et al. A machine learning-based protocol for efficient routing in opportunistic networks[J]. IEEE systems journal, 2018, 12(3): 2207-2213. DOI:10.1109/JSYST.2016.2630923 (  0) 0) |
| [15] |
YING Z, ZHANG C, LI F, et al. Geo-social: Routing with location and social metrics in mobile opportunistic networks[C]//2015 IEEE International Conference on Communications. London: IEEE Press, 2015: 3405-3410.
(  0) 0) |
| [16] |
JANG K, LEE J, KIM S K, et al. An adaptive routing algorithm considering position and social similarities in an opportunistic network[J]. Wireless networks, 2016, 22(5): 1537-1551. DOI:10.1007/s11276-015-1048-3 (  0) 0) |
| [17] |
WU J, YI X, CHEN Z G. Reducing energy consumption optimization selection of path transmission routing algorithm in opportunistic networks[J]. High technology letters, 2015, 25(3): 321-327. (  0) 0) |
| [18] |
SOBIN C C, RAYCHOUDHURY V, SAHA S. An energy-efficient and buffer-aware routing protocol for opportunistic smart traffic management[C]//Proceedings of the 18th International Conference on Distributed Computing and Networking. New York: ACM Press, 2017: 1-8.
(  0) 0) |
| [19] |
BASARAS P, IOSIFIDIS G, KATSAROS D, et al. Identifying influential spreaders in complex multilayer networks: a centrality perspective[J]. IEEE transactions on network science and engineering, 2019, 6(1): 31-45. DOI:10.1109/TNSE.2017.2775152 (  0) 0) |
| [20] |
FREEMAN L C. Centrality in social networks conceptual clarification[J]. Social networks, 1978, 1(3): 215-239. DOI:10.1016/0378-8733(78)90021-7 (  0) 0) |
| [21] |
WEI K M, LIANG X, XU K. A survey of social-aware routing protocols in delay tolerant networks: applications, taxonomy and design-related issues[J]. IEEE communications surveys & tutorials, 2014, 16(1): 556-578. (  0) 0) |
| [22] |
AHMAD T, LI X J, SEET B C, et al. Social network analysis based localization technique with clustered closeness centrality for 3D wireless sensor networks[J]. Electronics, 2020, 9(5): 738. DOI:10.3390/electronics9050738 (  0) 0) |
| [23] |
DING S, HIPEL K W, DANG Y G. Forecasting China's electricity consumption using a new grey prediction model[J]. Energy, 2018, 149: 314-328. DOI:10.1016/j.energy.2018.01.169 (  0) 0) |
| [24] |
马华东, 袁培燕, 赵东. 移动机会网络路由问题研究进展[J]. 软件学报, 2015, 26(3): 600-616. MA H D, YUAN P Y, ZHAO D. Research progress on routing problem in mobile opportunistic networks[J]. Journal of software, 2015, 26(3): 600-616. (  0) 0) |
| [25] |
GUO K, ZHANG Q S. Privacy preserving method based on GM(1, 1) and its application to clustering[J]. Grey systems: theory and application, 2012, 2(2): 157-165. DOI:10.1108/20439371211260135 (  0) 0) |
| [26] |
PRATIMA G, PARDASANI K R. A fast algorithm for mining multilevel association rule based on boolean matrix[J]. International journal on computer science & engineering, 2010, 2(3): 746-752. (  0) 0) |
| [27] |
SONI A, SAXENA A, BAJAJ P. A methodological approach for mining the user requirements using apriori algorithm[J]. Journal of cases on information technology, 2020, 22(4): 1-30. DOI:10.4018/JCIT.2020100101 (  0) 0) |
| [28] |
YUAN P Y, SONG M Y. MONICA one simulator for mobile opportunistic[C]//Proceedings of the 11th EAI International Conference on Mobile Multimedia Communications. Qingdao: EAI Press, 2018: 21-32.
(  0) 0) |
| [29] |
RHEE I, SHIN M, HONG S, et al. On the levy-walk nature of human mobility[J]. IEEE/ACM transactions on networking, 2011, 19(3): 630-643. DOI:10.1109/TNET.2011.2120618 (  0) 0) |
 2022, Vol. 54
2022, Vol. 54

