2. 国网山西省电力公司 信息通信分公司 山西 太原 030021
2. Information Communication Branch, State Grid Shanxi Electric Power Company, Taiyuan 030021, China
风能作为一种清洁的可再生能源, 其蕴量巨大, 已得到大力的发展。而风电机组的工作环境恶劣,导致故障频发,其中齿轮箱故障引起的停机维修时间长且维修费用高[1]。因此,实现风电机组齿轮箱的早期故障预警,可以帮助风电场工作人员实现预防性维修,降低运行的风险。监控与数据采集(supervisory control and data acquisition,SCADA)系统因其数据采集能力强、数据蕴含信息量大,在风电机组故障预警上得到广泛的研究[2]。魏乐等[3]基于贝叶斯优化和极限梯度提升算法建立模型,实现故障的早期预警,但单一模型的泛化能力和精度不足;黄荣舟等[4]利用多层LSTM网络构建融合SCADA数据的预测模型,通过3σ准则计算预警阈值,实现齿轮箱故障的有效预警,但只实现了单台风机的预警,对风电场的风机群不具有适用性;王梓齐等[5]基于模糊软聚类对风电机组齿轮箱的运行工况进行软划分,构造不同工况的非线性状态估计(nonlinear state estimate technique,NSET)模型,但没有消除聚类初始值对软模糊C均值(soft fuzzy C-means,SFCM)的影响;Singh等[6]针对聚类初始值对SFCM的影响,提出一种利用人工蜂群算法优化SFCM初始聚类中心的方法,提高了聚类的有效性;Abd-Elwahab等[7]利用相邻机组的相似工况,提出基于邻域比较法、K均值聚类的故障诊断方法,实现正常运行范围内的异常监测,但没有指出对所选相邻机组的确定方法。
基于上述研究,本文提出一种基于诱导有序加权平均(induced ordered weighted averaging,IOWA)算子组合模型的风电机组齿轮箱温度预警策略。基于群体多维特征相似性理论,进行相似风机群的划分;针对SFCM对初始值敏感的问题,采用遗传算法优化初始聚类中心;对运行数据进行工况划分并构造不同工况的NSET模型,不划分工况则采用LSSVM模型进行预测;最后基于IOWA算子进行组合预测,综合了NSET建模精度和LSSVM泛化能力,提高了预测的精度。
1 基础算法介绍 1.1 基于动态时间规整算法的相似度评价风电场中相同型号、相似风资源和相似运行状态的多台机组称为邻比机组,其在相同时刻的传感器测量输出也具有很大的相似性[8]。针对研究对象参与建模过程可能会造成数据泄露的问题[9],使用动态时间规整(dynamic time warping,DTW)算法分析风电场机群的风机相似度,对风电机组进行分群,选择出研究对象所在的邻比机组,采用群体中的其他风机数据进行模型构建,最大限度地保证所选研究对象的数据安全性。DTW算法使用动态规划分析两个时间序列的相似度,计算它们之间的最短距离[10]。其原理如下:设两个时间序列分别为A和B,构建一个n×m的矩阵,矩阵中的元素d(ai, bj)代表ai和bj两个点的欧氏距离。元素连续集为规整路径W,
| $ \begin{aligned} & \boldsymbol{W}=\left(w_1, w_2, \cdots, w_k\right), \\ & \max (n, m) \leqslant k<m+n-1 。\end{aligned} $ | (1) |
规整路径W要求的3种约束条件为边界条件、连续性和单调性。从满足上述条件的路径中选择最短累计距离的路径,
| $ {DTW}(A, B)=\min \left(\frac{\sum\limits_{k=1}^K w_k}{K}\right), $ | (2) |
式中:路径点的个数K补偿不同长度的规整路径。构造累计距离矩阵D(i, j),其表达式为
| $ \begin{aligned} & \boldsymbol{D}(i, j)=d\left(a_i, b_j\right)+\min [\boldsymbol{D}(i-1, j-1), \\ & \boldsymbol{D}(i-1, j), \boldsymbol{D}(i, j-1)] 。\end{aligned} $ | (3) |
初始条件为D(1, 1)=d(a1, b1)。从两个序列的起始点开始,根据式(2)和式(3)迭代计算,最终得到最小累加值D(n, m),该累加值即为时间序列A和B的最短累计距离DTW(A, B)。
1.2 最大信息系数特征分析最大信息系数(maximal information coefficient,MIC)是以信息论为基础的衡量变量间数据关联性的一种方式,具有通用性和公平性。它假定在相关变量的数据散点图上绘制网格,以度量二者间的相关性[11]。通过计算各网格的互信息来表征数据点落入网格的情况,在采用不同标准的网格划分下选取互信息的最大值作为最终的MIC值,其计算公式为
| $ \operatorname{MIC}(x ; y)=\max\limits_{a b<B} \frac{I(x ; y)}{\log _2 \min (a, b)}, $ | (4) |
式中:I(x; y)为x和y之间的互信息;a、b为在x、y方向划分网格的个数,而划分网格的最大值为B。
2 模糊聚类算法 2.1 软模糊C均值聚类FCM算法是一种以划分为基础的聚类算法[12],通过隶属度来对全部的数据进行划分,判定数据所属类别。FCM算法的目标函数为
| $ J\left(U, c_1, \cdots, c_c\right)=\sum\limits_{i=1}^c J_i=\sum\limits_{i=1}^c \sum\limits_{j=1}^n u_{i j}^m d_{i j}^2, $ | (5) |
式中:uij∈[0, 1];dij= ‖ ci-cj ‖为第i个聚类中心与第j个数据点间的欧氏距离;m∈[1, ∞)
为一个加权指数。使式(5)取最小值的目标函数为
| $ \begin{aligned} & \bar{J}\left(U, c_1, \cdots, c_c, \lambda_1, \cdots, \lambda_n\right)=J\left(U, c_1, \cdots, c_c\right)+ \\ & \sum\limits_{j=1}^n \lambda_j\left(\sum\limits_{i=1}^c u_{i j}-1\right)=\sum\limits_{i=1}^c \sum\limits_{j=1}^n u_{i j}^m d_{i j}^2+ \\ & \sum\limits_{j=1}^n \lambda_j\left(\sum\limits_{i=1}^c u_{i j}-1\right), \end{aligned} $ | (6) |
式中:λj (j=1, 2, …, n)是拉格朗日乘子。求式(5)的最小值要求:
| $ c_i=\frac{\sum\limits_{j=1}^n u_{i j}^m x_j}{\sum\limits_{j=1}^n u_{i j}^m}, $ | (7) |
| $ u_{i j}=\frac{1}{\sum\limits_{k=1}^c\left(\frac{d_{i j}}{d_{k j}}\right)^{\frac{2}{m-1}}}。$ | (8) |
软模糊C均值聚类算法是通过改进迭代过程的隶属度实现的[13],改进如下:
| $ \left\{\begin{array}{l} u_{i j}=1, u_{i j^{\prime}}=0, j^{\prime} \neq j, \\ u_{i j}=\max\limits_{1 \leqslant l \leqslant c} u_{i l}>\alpha, 0 <\alpha<1, \\ u_{i j}=\frac{1}{\sum\limits_{k=1}^c\left(\frac{d_{i j}}{d_{k j}}\right)^{\frac{2}{m-1}}} 。\end{array}\right. $ | (9) |
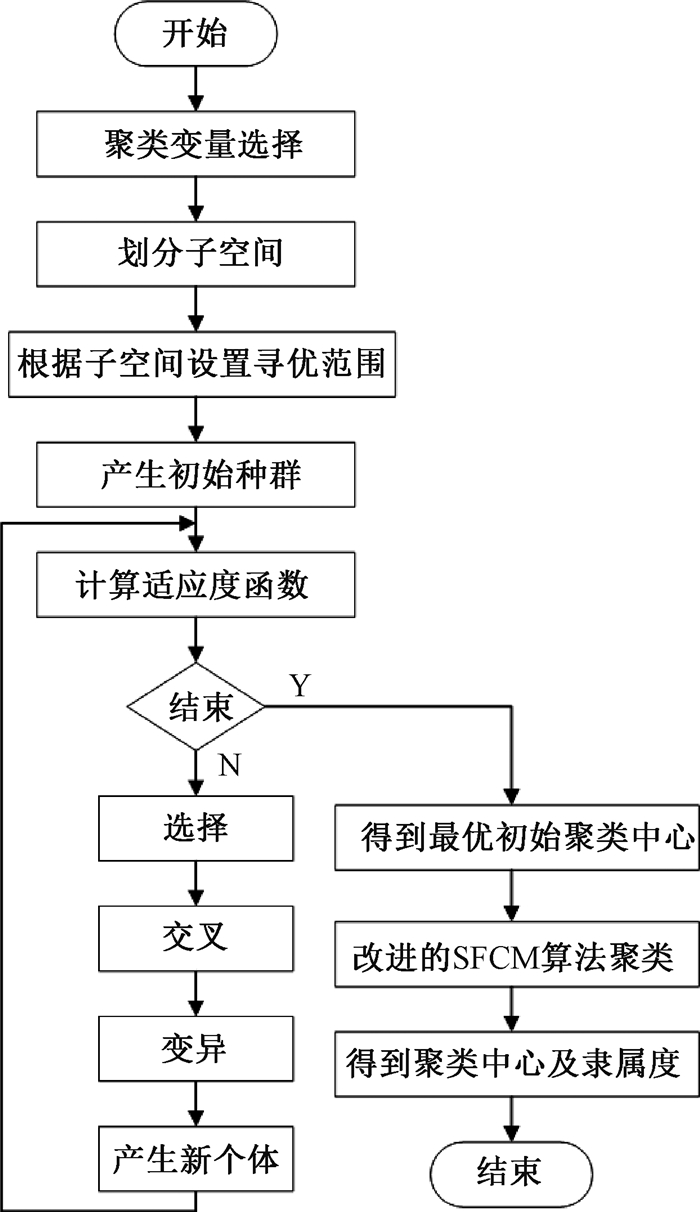
采用遗传算法(GA)优化软模糊C均值(SFCM)聚类的初始聚类中心,减少其对聚类结果的影响[14]。GA-SFCM聚类算法流程如图 1所示。
|
图 1 GA-SFCM聚类算法流程 Fig. 1 GA-SFCM clustering algorithm flow |
不变权的组合模型仅根据模型的类型进行模型权重的划分,各模型在整个预测区间的权重系数不变,使得在不同时间点的组合预测结果达不到最优[15]。因此,采用IOWA算子计算各单项模型的权重,得到变权的组合预测模型,最大程度地减少预测过程的误差[16]。
定义1 设二维数组(〈a1t, y1t〉, …, 〈ait, yit〉, …, 〈amt, ymt〉)是由时间点t下的m种单项模型的精度和预测值组成,并将数组中m个元素按照ait由大到小的顺序排列,则基于IOWA算子的组合模型预测值为
| $ \begin{aligned} & \hat{y}_{\text {IOWA }}=\left(\left\langle a_{1 t}, y_{1 t}\right\rangle, \left\langle a_{2 t}, y_{2 t}\right\rangle, \cdots, \left\langle a_{m t}, y_{m t}\right\rangle\right)= \\ & \sum\limits_{i=1}^m w_i y_{a-i n d e x(i t)}, \end{aligned} $ | (10) |
式中:a-index(it)为按照ait大小排序后t时刻第i个精度的下标。
定义2 定义ait为时间点t下第i种单项模型的预测精度,
| $ a_{i t}= \begin{cases}1-\left|\frac{y_t-y_{i t}}{y_t}\right|, & \left|\left(y_t-y_{i t}\right) / y_t\right| <1, \\ 0, & \left|\left(y_t-y_{i t}\right) / y_t\right| \geqslant 1 。\end{cases} $ | (11) |
令ea-index(it)=yt-ya-index(it),则以误差平方和最小为准则的组合模型最优化公式[17]为
| $ \begin{aligned} & \min S(w)=\sum\limits_{i=1}^m \sum\limits_{j=1}^m w_i w_j\left(\sum\limits_{t=1}^n e_{a-i n d e x(i t)} e_{a-i n d e x(j t)}\right), \\ & \text { s.t. } \sum\limits_{i=1}^m w_i=1, w_i \geqslant 0, i=1, 2, \cdots, m。\end{aligned} $ | (12) |
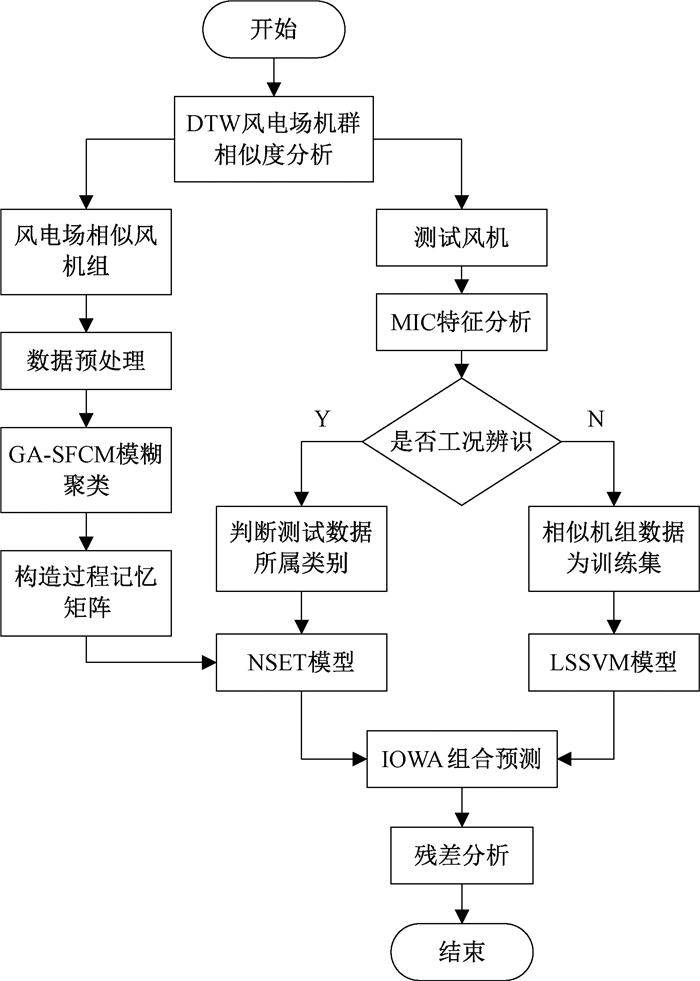
对风电场的风机进行基于DTW算法的相似度分析,划分出待测试风机及相似风机组,以相似风机组的正常工况数据作为构建预警模型的训练数据。采用GA-SFCM算法对正常工况数据进行聚类运算,构造不同的过程记忆矩阵,建立相应的NSET模型。依据工况辨识测试风机数据,得到NSET预测输出结果;而以相似风机组数据为训练集的LSSVM模型得到LSSVM预测结果。基于IOWA算子组合两种模型的预测结果,得到变权的组合预测模型,计算并分析预测结果与实际值之间的残差,实现对风电机组的故障检测。通过将测试机组与其邻比机组分开,提高了测试数据的独立性和邻比机组的数据利用率。风电机组齿轮箱温度预警流程如图 2所示。
|
图 2 风电机组齿轮箱温度预警流程 Fig. 2 Temperature warning flow of wind turbine gearbox |
选取国内某风场2016年8月的SCADA数据进行分析。该风场的采样频率为10 min,选择编号为S2_36的风机,以及与当前风机连续的8台风机。经风场工作人员证实,连续编号的风机表明其在风场中的地理位置、海拔高度相近。S2_36号风机在2016-08-31 16:33到2016-08-31 17:59由SCADA系统检测到故障:齿轮箱轴承温度高。
4.2 相似风电机群的判定选择编号连续的9台风机进行相似性判断。相似机群的判断准则包括地理位置、海拔高度,以及输入为风速、输出为功率的“黑箱”验证法。以S2_36号风机为研究对象,选择9台风机3 d的SCADA数据,使用DTW算法计算机组输入、输出的相似度数量级,结果分别列于表 1和表 2。可以看出,就S2_36号风机而言,S2_34、S2_35、S2_37号风机的相似度数量级小于其他风机,故认为S2_34、S2_35、S2_36、S2_37号风机为相似风电机群。选择S2_36号风机由SCADA系统测得的齿轮箱轴承温度故障前两天的288条数据为测试集,以S2_34、S2_35、S2_37号风机数据为训练集。数据预处理阶段剔除输出功率为零或者负值、风速小于切入风速(3 m/s)的点,认为这些数据点为非正常运行状态下的数据点。输入训练模型前将运行数据进行min-max数据归一化。
|
|
表 1 机组风速的相似度数量级 Tab. 1 Magnitude of similarity of unit wind speed |
|
|
表 2 机组功率的相似度数量级 Tab. 2 Magnitude of similarity of unit power |
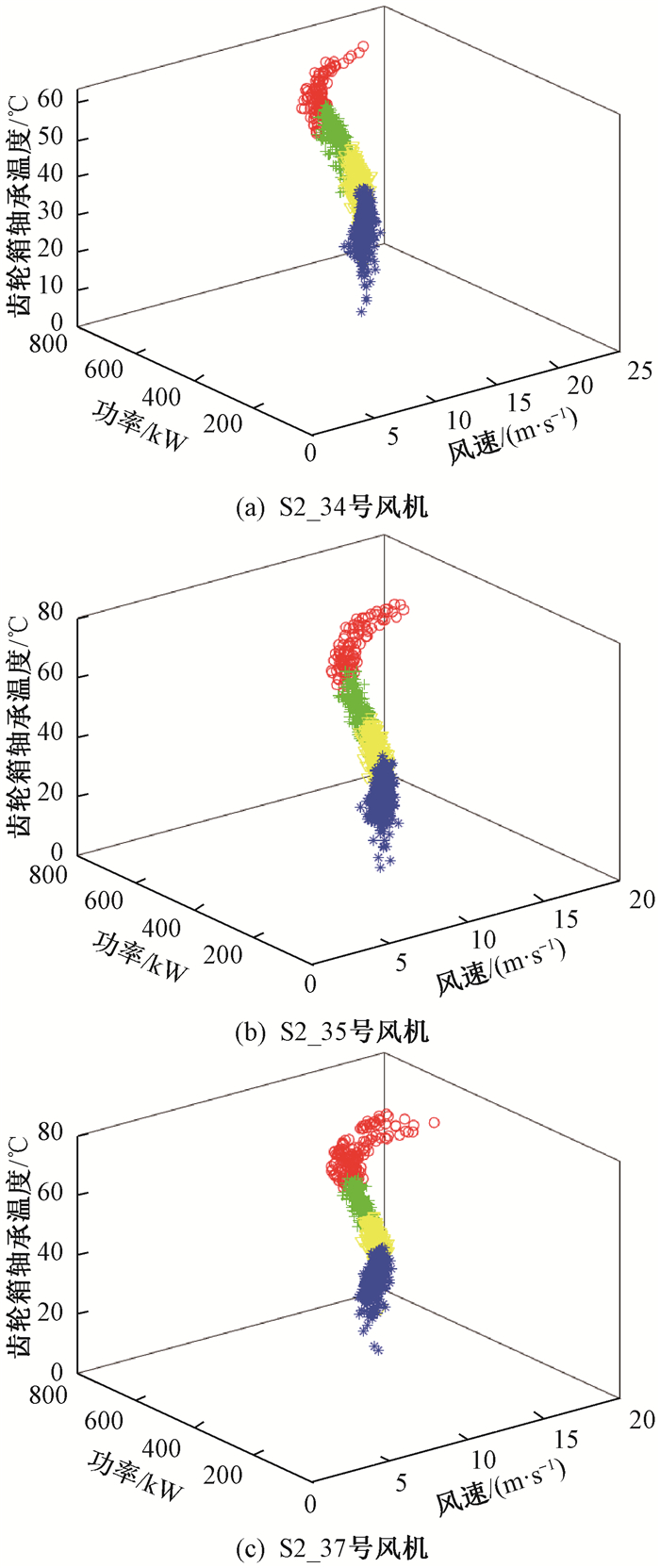
以齿轮箱轴承温度为研究对象,由于以风速为输入、有功功率为输出的“黑箱”模型能表征风机的运行状态,因此选择风速、有功功率和齿轮箱轴承温度为聚类变量。对S2_36号风机相似机群的其他风机正常工况数据进行聚类,3台风机的聚类结果如图 3所示。通过聚类结果可知,在所选的聚类变量作用下,可以得到不同工况下模型的训练集。
|
图 3 3台风机的聚类结果 Fig. 3 Clustering results of three fans |
计算3台风机SCADA数据的MIC值,求平均值后其降序排列结果如表 3所示。可以看出,前5项的MIC值大于0.5,故与齿轮箱轴承温度关联性强的变量有齿轮油温度、发电机温度、有功功率和风速。因此,确定辅助变量为风速、发电机温度、齿轮油温度和有功功率。
|
|
表 3 MIC值降序排列结果 Tab. 3 The MIC values arranged in descending order |
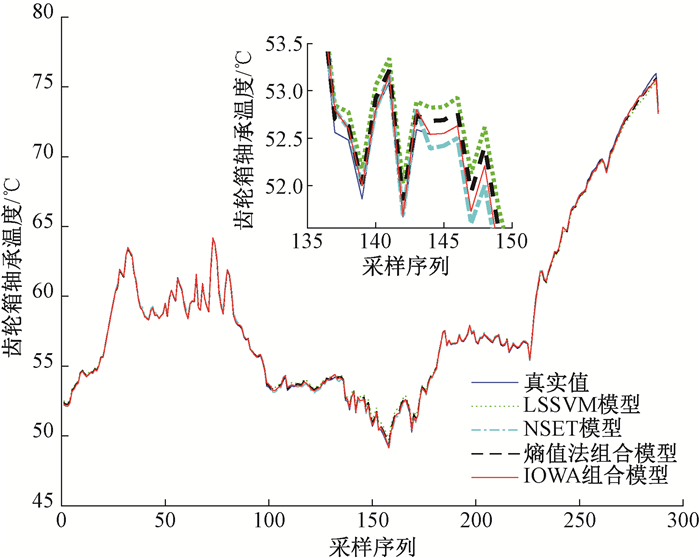
建立基于IOWA算子的组合模型进行温度预测,为证明该模型的有效性,还建立了LSSVM模型、NSET模型和熵值法组合模型进行对比分析。图 4为不同模型的预测结果。
|
图 4 不同模型的预测结果 Fig. 4 Prediction results of different models |
从图 4可以看出,单一模型的预测结果与真实值的偏离程度较大,而IOWA组合模型的预测结果与真实测量的结果更贴合。计算各模型的平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE),进行评价指标分析,结果列于表 4。
|
|
表 4 模型评价指标 Tab. 4 Model evaluation index |
由表 4可知,经过工况划分模糊聚类的NSET模型的预测效果优于不划分工况的LSSVM模型;对比熵值法组合模型,IOWA组合模型误差值小且预测结果更精确;相较LSSVM和NSET模型,经IOWA算子变权后的组合模型提高了预测精度,并且具有较高的泛化能力。
齿轮箱轴承温度的残差ε为
| $ \varepsilon=x-x^*, $ | (13) |
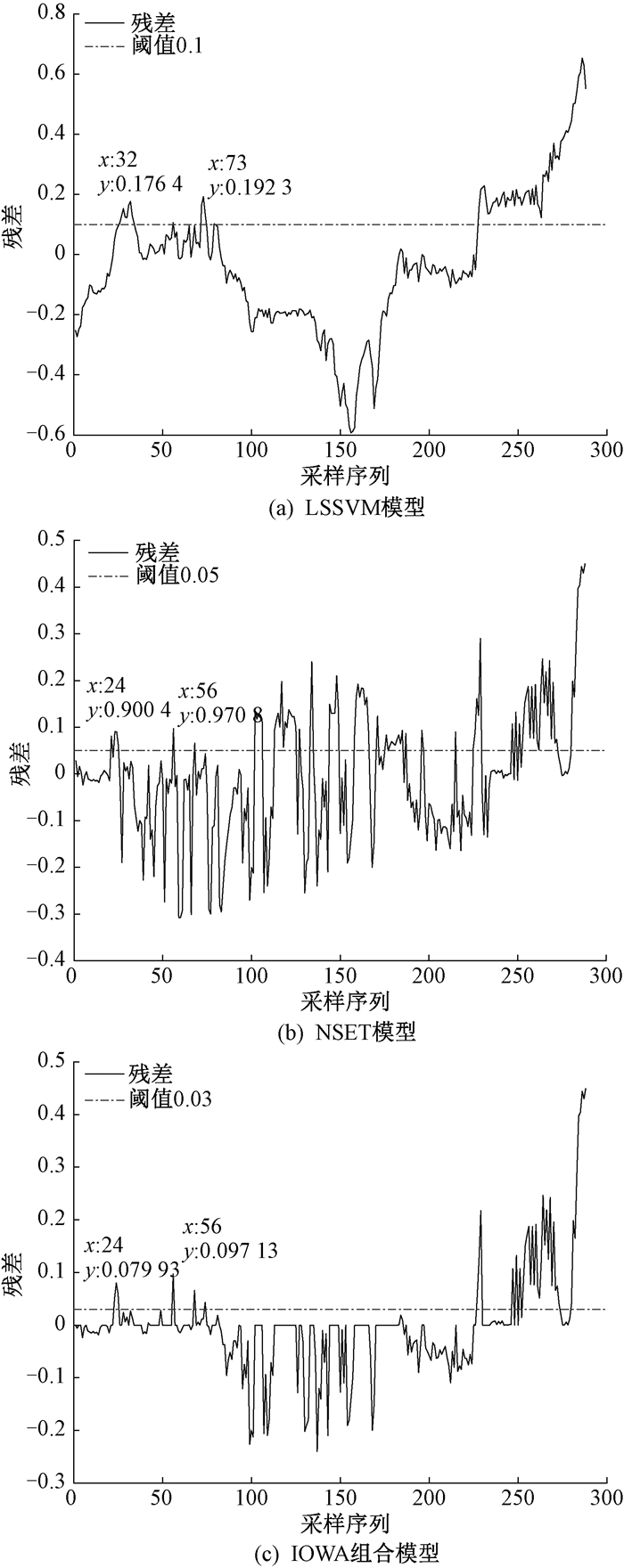
式中:x表示真实值;x*表示预测值。不同模型的残差分析结果如图 5所示。
|
图 5 不同模型的残差分析 Fig. 5 Residual analysis of different models |
从图 5(a)可以看出,没有划分工况的LSSVM模型的残差很好地保持了原数据的波动情况,具有较好的时间连续性,但LSSVM模型的预测精度较低。其在数据点32处达到第一个波峰,此处可作预警点;在数据点73处,残差再次超过设定的阈值,此处可作报警点。从图 5(b)可以看出,NSET模型的残差值小于LSSVM模型,预测精度更高。其在数据点24处超出阈值,达到第一个波峰,此处可作预警点;在数据点56处再次达到波峰,此处可作报警点。从图 5(c)可以看出,IOWA组合模型的波形频率较NSET模型大大降低,使得数据点的有效性增强,强化了预警的准确性和可靠性。其在数据点24处第一次超出阈值,此处可作预警点;在数据点56处再次超出阈值,此处可作报警点。
5 结束语本文利用DTW算法选择出工况相近的风机组,基于MIC值进行影响齿轮箱轴承温度变化的特征选择,采用IOWA算子进行预测结果的整合,提高了模型的预测性能。风电场监测数据研究结果表明:基于DTW算法选择工况相近的风电机群,使所要研究的对象风机不参与整个建模过程,最大程度地保护了数据的安全性和完整性;采用遗传算法优化的软模糊C均值聚类后,使用非线性状态估计建立预测模型,降低了记忆矩阵的数据规模,提高了数据的利用率,减少了计算时间;通过IOWA算子的组合,使得预测结果综合NSET和LSSVM模型的特点,提高了预测精度。但本文提出的故障检测方法只对齿轮箱部位进行了研究,而对其他故障频发的部件是否适用仍需要进一步的确定。
| [1] |
陈雪峰, 郭艳婕, 许才彬, 等. 风电装备故障诊断与健康监测研究综述[J]. 中国机械工程, 2020, 31(2): 175-189. CHEN X F, GUO Y J, XU C B, et al. Review of fault diagnosis and health monitoring for wind power equipment[J]. China mechanical engineering, 2020, 31(2): 175-189. (  0) 0) |
| [2] |
ENCALADA-DÁVILAÁ, PURUNCAJAS B, TUTIVÉN C, et al. Wind turbine main bearing fault prognosis based solely on SCADA data[J]. Sensors, 2021, 21(6): 2228. DOI:10.3390/s21062228 (  0) 0) |
| [3] |
魏乐, 胡晓东, 尹诗. 基于优化XGBoost的风电机组发电机前轴承故障预警[J]. 系统仿真学报, 2021, 33(10): 2335-2343. WEI L, HU X D, YIN S. Optimized-XGBoost early warning of wind turbine generator front bearing fault[J]. Journal of system simulation, 2021, 33(10): 2335-2343. (  0) 0) |
| [4] |
黄荣舟, 汤宝平, 杨燕妮, 等. 基于长短时记忆网络融合SCADA数据的风电齿轮箱状态监测[J]. 太阳能学报, 2021, 42(1): 235-239. HUANG R Z, TANG B P, YANG Y N, et al. Condition monitoring of wind turbine gearbox based on LSTM neural network fusing SCADA data[J]. Acta energiae solaris sinica, 2021, 42(1): 235-239. (  0) 0) |
| [5] |
王梓齐, 刘长良, 刘帅. 基于集成NSET和模糊软聚类的风电机组齿轮箱状态监测[J]. 仪器仪表学报, 2019, 40(7): 138-146. WANG Z Q, LIU C L, LIU S. Condition monitoring of wind turbine gearbox based on ensemble nonlinear state estimation technique and soft fuzzy clustering[J]. Chinese journal of scientific instrument, 2019, 40(7): 138-146. (  0) 0) |
| [6] |
SINGH T I, LAISHRAM R, ROY S. Combined spatial FCM clustering and swarm intelligence for medical image segmentation[EB/OL]. [2021-09-21]. https://www.researchgate.net/publication/311855432.
(  0) 0) |
| [7] |
ABD-ELWAHAB K T, HASSAN A A. SCADA data as a powerful tool for early fault detection in wind turbine gearboxes[J]. Wind engineering, 2021, 45(5): 1317-1326. DOI:10.1177/0309524X20969418 (  0) 0) |
| [8] |
郭鹏, 姜漫利. 基于邻比模型分析的风电机组传感器监测研究[J]. 太阳能学报, 2018, 39(5): 1402-1407. GUO P, JIANG M L. Wind turbine sensor monitoring based on neighbor comparison model[J]. Acta energiae solaris sinica, 2018, 39(5): 1402-1407. (  0) 0) |
| [9] |
DIAGO C, FORSHAW A. Cybersecurity for shared infrastructure substation networks with IEC 61850 GOOSE and sampled values[J]. The journal of engineering, 2018(15): 1195-1198. (  0) 0) |
| [10] |
陈诗佳, 王楚豫, 谢磊. 基于智能手环运动状态的音乐生成系统[J]. 郑州大学学报(理学版), 2021, 53(4): 95-101. CHEN S J, WANG C Y, XIE L. Music generation system based on movement state of smart bracelet[J]. Journal of Zhengzhou university (natural science edition), 2021, 53(4): 95-101. (  0) 0) |
| [11] |
ZHENG K F, WANG X J, WU B, et al. Feature subset selection combining maximal information entropy and maximal information coefficient[J]. Applied intelligence, 2020, 50(2): 487-501. (  0) 0) |
| [12] |
王杰, 刘向晴. 彩色图像分割的FCM预分类核极限学习机方法[J]. 郑州大学学报(理学版), 2018, 50(2): 75-80. WANG J, LIU X Q. FCM pre-classification kernel extreme learning machine algorithm of color image segmentation[J]. Journal of Zhengzhou university (natural science edition), 2018, 50(2): 75-80. (  0) 0) |
| [13] |
甄成刚, 刘怀远. 基于多模型聚类集成的锅炉烟气NOx排放量预测模型[J]. 热力发电, 2019, 48(4): 33-40. ZHEN C G, LIU H Y. Prediction model of NOx emission from coal-fired boiler based on multi-model clustering ensemble[J]. Thermal power generation, 2019, 48(4): 33-40. (  0) 0) |
| [14] |
赵文杰, 吕猛. 基于多LS-SVM集成模型的锅炉NOx排放量建模[J]. 电子测量与仪器学报, 2016, 30(7): 1037-1044. ZHAO W J, LV M. NOx emission modeling of coal-fired boiler based on multi LS-SVM ensemble model[J]. Journal of electronic measurement and instrumentation, 2016, 30(7): 1037-1044. (  0) 0) |
| [15] |
赵亚红, 王金星, 张丽华, 等. 基于IOWHA算子的路基沉降加权组合预测方法研究[J]. 铁道科学与工程学报, 2018, 15(10): 2529-2534. ZHAO Y H, WANG J X, ZHANG L H, et al. Study on weighted combination model based on IOWHA operator in prediction of subgrade settlement[J]. Journal of railway science and engineering, 2018, 15(10): 2529-2534. (  0) 0) |
| [16] |
FLORES-SOSA M, AVILÉS-OCHOA E, MERIGÓ J M, et al. Volatility GARCH models with the ordered weighted average (OWA) operators[J]. Information sciences, 2021, 565: 46-61. (  0) 0) |
| [17] |
甄成刚, 张争鹏. 基于VMD分解与MIC特征分析的风电功率组合预测[J]. 郑州大学学报(理学版), 2022, 54(3): 88-94. ZHEN C G, ZHANG Z P. Wind power combination prediction based on VMD decomposition and MIC feature analysis[J]. Journal of Zhengzhou university (natural science edition), 2022, 54(3): 88-94. (  0) 0) |
 2023, Vol. 55
2023, Vol. 55


