0 引言

随着先进移动设备以及无线网络的普及，出现了一种新的众包方式——空间众包(spatial crowdsourcing，SC)^[1-2]。SC系统由一群工人、一个云平台和需求者组成，平台负责发布各种与位置相关的空间任务，工人可以自身移动到这些位置并完成相关的空间任务^[3]。SC可以完成大量个人用户无法应对的空间任务，已广泛应用于诸多领域。如何将这些任务分配给工人成为当前SC研究的主要问题^[4]。现有的SC研究和技术工作一般聚焦在普通空间任务上，这些任务可以由非专业劳动者完成，例如众包灾难响应和新闻报道。随着任务的多样化，寻找具有专业知识且质量高的工人完成特定空间任务成为SC任务分配的目标之一，例如某景点的法语解说工作^[5]。同时，人们开始关注任务的完成质量，这意味着平台需要明确任务和工人属性，以便精准分配和高效完成任务。

当前研究中一般单纯考虑任务是否分配或工人的专业知识是否与任务相匹配^[6]，导致平台很可能将一个难度较大的任务分配给一个水平不够或信誉度较低的工人。若没有考虑工人是否能够胜任，即无法得知该工人成功完成任务的概率，必然会影响任务完成率以及精确分配分数等评价指标。其中，最大化任务分配数量(maximum task assignment, MTA)是大部分工作的首要目标^[7]，其主要算法有两种：一为二分图匹配。当不考虑工人任务时限问题并假设所有工人皆能可靠完成任务时，便转化为二分图匹配问题。二为定义位置熵。即将问题转化为最小成本最大流问题^[8]。由此可见，MTA局限于关注任务是否被分配，并不考虑工人是否具备能力。于是文献[7]提出最大化匹配分数(maximum score assignment, MSA)问题。MSA方法为工人与任务随机设定技能整数值，因此问题目标成为在考虑工人专业知识背景下探索任务分配问题。但MSA仅加入了工人技能属性，并未考虑工人效用值(代表工人可靠性)的不同会在很大程度上影响任务的完成率。若能够在分配前得到工人完成某类任务的成功概率值(效用值)，则能够有效避免由于工人质量未知而导致匹配成功率降低的问题。因此，本文提出一种用于SC任务匹配的未知工人效用估计方法，基于多臂老虎机(multi-armed bandit，MAB)模型进行工人效用值计算，实现对任务和工人的高质量匹配，采用两阶段算法解决带有效用的最高分数匹配(maximum score assignment with utility, MSAU)问题。阶段一在MAB模型的基础上，利用具有臂特征的有界LinUCB算法^[9]，解决传统MAB算法在求解SC中工人与任务个体间存在很大差异时的异常收敛及相同属性臂问题；阶段二采用改进的分配加分方式, 将效用值带入精确分配分数的计算中，定义新的加分方式与完成概念，清晰展现了在考虑工人效用值后带给任务分配的积极影响。使用来自MovieLens和Gowalla数据集的真实历史用户数据，验证了带有工人效用的任务匹配模型对任务分配评价指标有很大程度的提高。

1 MAB模型介绍

MAB是一类处理不确定性决策问题的模型，非常适合解决专家众包问题。在SC背景下，玩家类比于任务，老虎臂类比于工人，动作类比于工人任务进行一次匹配。在优化过程中，工人最初具有未知奖励，必须通过嘈杂的试验来学习，其目标是通过依次选择不同的动作来最大化奖励总量^[10-12]。MAB模型中最著名的一个方法是上界置信区间(upper confidence bound，UCB)，UCB通过严格的理论论证可达到接近理论最优的整体收益。但UCB需要尝试一遍所有臂，因此当臂数量很多时会出现过早收敛的问题，而且UCB并未充分利用环境信息。

“Yahoo!”科学家们加入特征信息，提出了基于UCB的LinUCB算法^[9]，不再仅仅是根据实验估算置信区间，而是结合了特征信息。然而LinUCB算法依旧存在一个问题：由于需要计算每一个候选臂的期望收益和置信区间，因此同时处理的候选臂数量不能过大。在后续研究中，科学家们陆续提出了一些避免臂数量过多而导致收敛问题的算法。例如与协同过滤算法结合^[13-14]，采用协同聚类使玩家和老虎臂两种协同方式同时进行等。本文利用MAB模型估计工人的效用值，在解决了Genius Rocket站点需要劳动密集型手动选择问题的同时，也避免出现由于未知工人质量而导致分配数量和质量降低的情况。

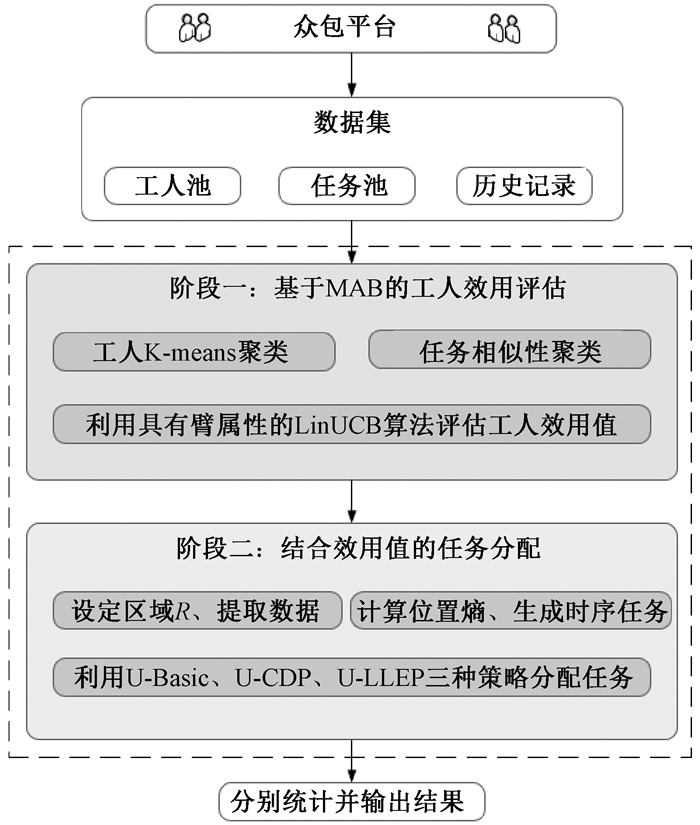
2 两阶段模型

图 1为用于SC任务匹配的未知工人效用评估方法框架，主要分为两个阶段。

2.1 阶段一：基于MAB的工人效用评估

在评估工人效用时，采用时间复杂度为O(n³)的LinUCB算法，以老虎机一轮游戏模拟一次为任务选择工人的过程，玩家作任务，老虎臂作工人，动作作匹配过程，通过依次选择不同老虎臂来最大化分配数量。

计算工人效用的MAB算法思想如下：根据先前试验中观察到的收益选择臂a并得到收益r_{t, at}，收益的期望值取决于用户u_t和臂a_t，则模型总收益表示为$\sum\limits_{t = 1}^T {{r_{t, {a_t}}}} $，最佳期望收益表示为$E\left[ {\sum\limits_{t = 1}^T {{r_{t, a_t^*}}} } \right]$，其中r_{t, at^*}代表实验t时具有最大预期收益的臂。令D_a为t时维度为m×d的矩阵，其行对应m个训练输入(例如先前对臂a观察到的m个属性)，b_a∈R^m为相应的响应向量(例如相应的m次点击/非点击用户的反馈)，c_a表明算法计算的臂a的相应置信区间。实验中假设臂a的预期收益在其d维特征矩阵x_{t, a}中是线性的，并且具有未知的矢量系数θ_a，将岭回归应用于训练数据(D_a, c_a)，可以得出矢量系数的估计值为

$ {\theta _a} = {\left( {\mathit{\boldsymbol{D}}_a^{\rm{T}}{\mathit{\boldsymbol{D}}_a} + {\mathit{\boldsymbol{I}}_d}} \right)^{ - 1}}\mathit{\boldsymbol{D}}_a^{\rm{T}}{c_a}。$

(1)

则对于所有的实验t，有

$ E\left[ {{r_{t, a}}|{\mathit{\boldsymbol{x}}_{t, a}}} \right] = \mathit{\boldsymbol{x}}_{t, a}^{\rm{T}}\theta _a^*。$

(2)

最后可以得出UCB类型的带有工人效用值计算的MAB算法选择策略，在每轮实验t，

$ {a_t} = \arg \;\mathop {\max }\limits_{a \in {\mathit{\boldsymbol{A}}_t}} \left( {\mathit{\boldsymbol{x}}_{t, a}^{\rm{T}}{\theta _a} + \alpha \sqrt {\mathit{\boldsymbol{x}}_{t, a}^{\rm{T}}\mathit{\boldsymbol{A}}_a^{ - 1}{\mathit{\boldsymbol{x}}_{t, a}}} } \right), $

(3)

其中：A_a= D_a^TD_a+ I_d。

效用值估计算法(算法1)的具体步骤如下。

算法 1  效用值估计

输入：输入矩阵A，参数a。

输出：效用值u_{i, j}。

for i=1, 2, …, T do

  计算所有臂的特征值j∈A_i: x_{i, j}∈ R^d

    for j∈ A_i do

      if a is new then

        A_j← I_d

        b_j← O_d×1

      end if

        ${\mathit{\boldsymbol{\hat \theta }}_j} \leftarrow \mathit{\boldsymbol{A}}_j^{ - 1}{\mathit{\boldsymbol{b}}_j}$

          ${u_{i, j}} \leftarrow \mathit{\boldsymbol{\hat \theta }}_j^{\rm{T}}{\mathit{\boldsymbol{x}}_{i, j}} + a\sqrt {\mathit{\boldsymbol{x}}_{i, j}^{\rm{T}}\mathit{\boldsymbol{A}}_j^{ - 1}{\mathit{\boldsymbol{x}}_{i, j}}} $

    end for

    选择j_i=$\arg \;\mathop {\max }\limits_{j \in {\mathit{\boldsymbol{A}}_i}} {u_{i, j}}$的臂, 并记录回报值r_i

    A_ij← A_ij+ x_{i, j} x_{i, j}^T

    b_ij← b_ij+r_ix_{i, j}

end for

2.2 阶段二：结合效用值的任务分配 2.2.1 问题定义

为了体现工人质量作用以及明确表示分配方式的改变，进行了如下定义。

定义1  时空任务。时空任务t的形式为〈l, s, Entropy(l), Skill〉, 其中l表示任务t经纬度；s表示时间片；Entropy(l)表示位置熵；Skill表示任务t所需技能。

定义2  工人。工人w的形式为〈id, T_max, R, l, Skill, u_ij〉, 其中id表示唯一确定工人身份的编号；T_max表示工人w最多可接受任务数量；R表示接受范围；l表示工人w经纬度；Skill表示工人w所具备技能；u_ij表示工人i对任务j的效用值。

定义3  技能匹配。若工人完成任务的效用值大于阈值p且技能相符，即u_ij>p∧Skill_w=Skill_t时，方可认为工人任务符合技能匹配。

定义4  任务完成。当工人对应分配任务的效用值小于阈值时，即u_ij < p，认为工人i无法完成任务j。

定义5  分数。为了衡量分配情况，定义分数概念，并将加分方式^[7]

$ \left\{ {\begin{array}{*{20}{c}} {{x_{ij}} = 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Score = 0}\\ {{x_{ij}} = 1 \wedge Skil{l_w} \ne Skil{l_t}, \;\;\;\;\;\;Score = 1}\\ {{x_{ij}} = 1 \wedge Skil{l_w} = Skil{l_t}, \;\;\;\;\;\;Score = 3} \end{array}} \right., $

更改为

$ \begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {{x_{ij}} = 0, \vee \left( {{x_{ij}} = 1 \wedge p < 0.4} \right), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Score = 0}\\ {{x_{ij}} = 1 \wedge Skil{l_w} \ne Skil{l_t} \wedge p > 0.4, \;\;\;\;\;\;\;\;\;\;Score = 1}\\ {{x_{ij}} = 1 \wedge Skil{l_w} = Skil{l_t} \wedge p > 0.4, \;\;\;\;\;\;\;\;\;Score = 3} \end{array}} \right., \\ \end{array} $

其中：x_ij为指示变量，${x_{ij}} = \left\{ {\begin{array}{*{20}{c}} {0, \;\;\;分配成功}\\ {1, \;\;\;分配不成功} \end{array}} \right.$。

定义6  带有效用的最高分数匹配(MSAU)。令时间片ϕ={s₁, s₂, …, s_n}，S_i表示s_i时刻的分配总分数，且${S_i} = \sum\limits_{j = 1}^{\left| {{I_i}} \right|} {Scor{e_j}} $，那么MSAU目标为$\sum\limits_{i = 1}^n {{S_i}} $。

任务分配算法(算法2)的具体步骤如下。

算法 2  任务分配

输入：输入工人和任务矩阵W_si、T_si以及参数r，并输入策略类型algorithm，开始和截止时间startTime、endTime。

输出：工人任务对WT_final={〈w₁, t₁〉, …, 〈w_n, t_n〉}。

1.  for s_i←startTime to endTime do

      初始化工人矩阵W = W_si、有效工人矩阵W_available=ϕ、有效任务矩阵T_available=ϕ

      初始化w′_i个候选时空任务集T_wi=ϕ

2.    for w_j∈ W_others do

3.            if w_j.timeStamp=s_i then W ←w_j

4.        for w_i∈ W do

5.                    for t_j∈ T_si do

6.                        if distance(w_i, t_j)≤r then T_wi←t_j, T_available←t_j

7.                      if T_wi=ϕ, W_available←w_i

8.    将W_available和T_available代入最大权重匈牙利算法，求出WT和最大得分Score

9.    if algorithm=U-Basic then WT=WT_final

10.    else if algorithm=U-CDP then

    $\min \sum\limits_{j, k} {{x_{j, k}}} \times \mathit{distance}\left( {{w_j}, {t_k}} \right)$

    ${\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\sum\limits_{j, k} {{x_{j, k}} \times Score\left( {{w_j}, {t_k}} \right)} = Score$

    $\forall {w_j} \in {\mathit{\boldsymbol{W}}_{{\rm{available}}}}\sum\limits_k {{x_{j, k}}} \le 1, \forall {t_k} \in {\mathit{\boldsymbol{T}}_{{\rm{available}}}}\sum\limits_j {{x_{j, k}} \le 1} $

11.    else if algorithm=U-LLEP then

    $\min \sum\limits_{j, k} {{x_{j, k}}} \times Entropy\left( {{w_j}, {t_k}} \right)$

    ${\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\sum\limits_{j, k} {{x_{j, k}} \times Score\left( {{w_j}, {t_k}} \right)} = Score$

    $\forall {w_j} \in {\mathit{\boldsymbol{W}}_{{\rm{available}}}}\sum\limits_k {{x_{j, k}}} \le 1, \forall {t_k} \in {\mathit{\boldsymbol{T}}_{{\rm{available}}}}\sum\limits_j {{x_{j, k}} \le 1} $

使用CPLEX求解器找到当前的最终解WT_final，更新工人信息，W_others←w。

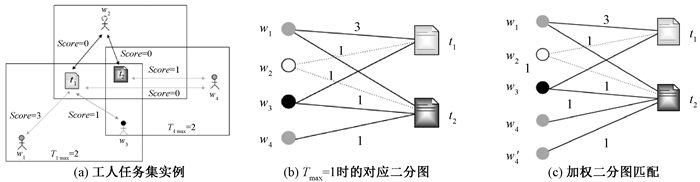
图 2为MSAU分配实例示意图。在图 2的实例中，产生符合定义4与定义5的分配结果。当满足效用值阈值且技能属性相同，即Skill_w=Skill_t∧p>0.4时，Score=3的分配对有〈w₁, t₁〉；当满足效用值阈值但技能属性不同，即Skill_w≠Skill_t∧p>0.4时，Score=1的分配对有〈w₃, t₁〉、〈w₄, t₂〉；当不满足效用值阈值或工人任务不在范围区域R内，即x_ij=1∧p < 0.4时，Score=0的分配对有〈w₂, t₁〉、〈w₂, t₂〉、〈w₄, t₁〉。

2.2.2 三种分配策略

本文提出带有效用的、时间复杂度为O(n³)的基本方法(U-Basic)。U-Basic方法意在每个时间片上进行任务最大分配，同时实现最大完成数量分配的目标，并将此称为MSAU实例问题。解决MSAU实例问题的思路是利用工人任务的约束，包括空间区域R、可接受任务的最大数量T_max以及工人效用值u_ij来确保正确分配任务。若无约束，则可能会导致工人分配远距离任务以及无法高质量完成任务等问题。这意味着每个工人都愿意执行R内的最多T_max任务，且只有满足一定u_ij时方可算为分配成功。图 2(b)为图 2(a)当T_max=1时的对应二分图，工人w₂在其范围区域接受任务(t₁, t₂)，而w₄可接受任务为t₂。因此，有两条边连接w₂，一条边连接w₄，虚线代表Score=0的情况。图 2(c)为图 2(b)的加权二分图匹配，约束条件为T_4max=2的w₄被两个具有T_4max=1约束的w′₄取代。由此可使用匈牙利算法进行分配，Basic方法意在每个时间片上进行任务最大分配，然而仅实现局部优化，如算法2中步骤9所示。因此，U-Basic方法仅能够得到局部最优解，MSAU在每个时间片不一定会得到全局最优答案。

为了改进基本策略，提出带有效用的最小位置熵方法(U-LLEP)和带有效用的近距离优先方法(U-CDP)。位置熵考虑了该任务所在位置的工人总数，以及工人们未来访问该位置的相对比例。如果工人们以相同的速率访问某位置，则该位置的熵较高，反之则较低。因此，将位置熵较小区域中的任务给予更高的优先级，那么这些任务被其他工人完成的可能性较低。在图 2(c)中，令Entropy(l₂)为空间任务t₂的位置熵。t₂位于所有工人的空间区域中，因此将连接到t₂的所有边的成本设置为Entropy(l₂)。U-LLEP问题等价于解决每个时间片的最小成本问题，首先使用匈牙利算法找到最大匹配项，然后使用CPLEX求解器解决此问题，如算法2中步骤11所示。U-Basic和U-LLEP方法都试图最大化任务分配数量，却在分配过程中没有考虑工人的差旅费用(例如时间或距离)。

U-CDP的目标是在每个时间片最大化任务分配数量的同时，尽可能地减少工人的差旅成本。实验中根据工人之间的欧氏距离，定义工人w和空间任务t之间的旅行成本d(w, t)，通过计算每个工人与其区域内空间任务之间的距离，将较高的优先级与较接近的任务相关联。于是，该问题演变为最低成本的MSAU实例问题，如算法2中步骤10所示。

3 实验部分 3.1 实验数据集

实验的两个阶段分别采用MovieLens和Gowalla数据集。MovieLens数据集(https://movielens.org)包括电影推荐服务的5星评级和自由文本标记活动，包含9 742部电影的100 836个评级和3 683个标签应用程序，这些数据由610位用户在1996年3月29日到2018年9月24日之间创建。该数据集于2018年9月26日生成，信息包括用户与电影属性以及影评记录。本实验利用MovieLens数据集9 826个任务信息、1 297个工人信息和100 005个历史信息进行计算，并将α设定为0.1。Gowalla是一个基于位置的社交网络，用户可以在其中登录附近的不同地点，签入包括用户地点的位置和时间，所用数据集包含了2009年2月至2010年10月之间的6 442 890条记录数据，信息包括工人id以及打卡经纬度与时间。实验假设用户是SC系统的工人，签到某个位置等效于在该位置接受空间任务。利用MovieLens数据集为用户推荐电影映射SC背景下的任务寻找工人；利用Gowalla数据集为工人、任务随机分配经纬度，完成实验第一阶段的工人效用值评估以及第二阶段的任务分配。

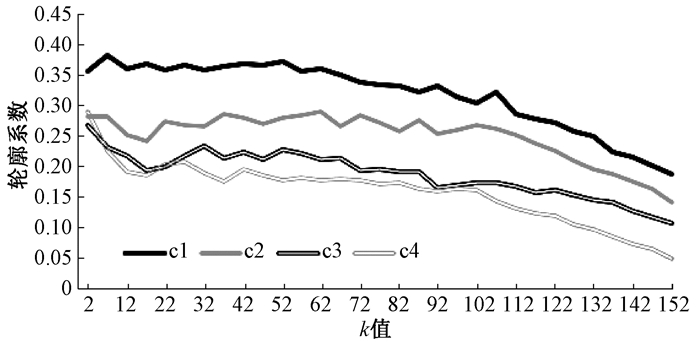
3.2 实验内容

工人聚类时，利用欧氏距离计算工人相似度。任务聚类时，利用轮廓系数s_i衡量聚类结果，K-means聚类结果示意图如图 3所示。采用不同的特征提取进行聚类，选择c1特征提取结果，通过寻找较大的s_i，可以得到合适的k值如7、22、27、32等(每次运行时稍微不同)。在本文实验中，选择k=7。将聚类后的结果应用于MAB算法，首先计算簇间效用值，然后选择Top-1工人簇i进行工人与任务的一对一计算，最后输出工人效用值，并给予更新。

特征矩阵X(x_ij∈ X)用来表示工人对任务的偏好程度，用工人簇与任务簇数据构造，其中x_ij=n_ij，n_ij表示在历史记录数据中工人簇i(i∈k_w)曾访问任务簇j(j∈k_t)的数目，k_w、k_t分别表示工人簇和任务簇的数量。为了减少奇异数据对实验效果的影响，对矩阵X进行了归一化处理。

3.3 实验结果分析

设置p=0.4，表 1列出了6个评价指标(总分配任务数、精确匹配任务数、精确匹配占比、任务总完成数、总完成占比和总距离)在使用效用值(表中用“使用u_ij”代替)和不使用效用值(表中用“未使用u_ij”代替)时的实验结果。

从表 1可以看出，加入u_ij后，对于总分配任务数评价指标，U-CDP和U-LLEP方法展现出明显优势且彼此相差不大。而对于精确匹配任务数评价指标，U-LLEP和U-CDP方法均优于U-Basic方法。在总距离评价指标方面，U-CDP方法最佳。对于没有使用u_ij的原实验，在精确匹配数量方面LLEP方法最优；在距离方面CDP方法最佳。这表明加入u_ij的实验并不会对分配策略的结果有太大影响。

加入u_ij后，U-CDP和U-LLEP方法的评价指标如总分配任务数、精确匹配任务数和任务总完成数都较不考虑u_ij的情况有大幅度提升。对于U-CDP和U-LLEP方法，总分配任务数的增幅大于40%，精确匹配任务数的增幅大于60%。U-CDP方法的精确匹配占比增加11.70%，U-LLEP方法增加8.00%。U-Basic与U-CDP方法的任务总完成数约为原实验的5倍，U-LLEP方法约为原实验的4倍；同样，U-Basic、U-CDP、U-LLEP方法的总完成占比分别增加约25%、13%、17%。说明当考虑了u_ij后，系统将任务分配给具有相对更高质量的工人，既保证了分配的数量又保证了分配的质量。

4 小结

本文提出一个用于SC任务匹配的未知工人效用评估方法，基于具有上下文的MAB模型，并为老虎臂和玩家加入特征元素，使其更符合SC的问题背景。在原有单纯考虑任务分配解决MTA、MSA问题的基础上，做到事先评估工人质量，得到工人效用值后，在真实数据集上分别采用三种策略进行分配，并利用多项评价指标进行对比分析，验证了当考虑工人质量的情况下不仅可以保证分配质量，也可以提高分配数量。同时，加入工人与任务的多种属性，使用聚类方法增强了传统MAB算法的扩展性。但本文牺牲了部分距离来换取更多的分配数目，在接下来的研究中将寻找合适的方法解决总路程问题。此外，将会增加实验原始对偶框架与本文方法的对比实验，考虑增加新的评价标准如花销与预算，寻找在预算有限条件下的最优方法等。