高效用模式挖掘(high utility pattern mining, HUPM)[1]问题描述为挖掘效用值不低于用户定义的最小效用阈值(minimum utility threshold, minutil)的所有模式,目前已取得了大量的研究成果,但在实际应用中仍存在一些局限性,由此衍生出了一些高效用扩展模式,例如旨在从动态数据库中挖掘高效用项集(high utility itemsets, HUIs)的增量HUPM算法[2-4];考虑商品保质期和效用值的on-shelf HUPM算法[5-7];考虑项集长度和效用值的高平均HUPM算法[8-10];不需要设置minutil的top-k HUPM算法[11-13]以及可处理含负项的HUPM算法[14-15]。基于数据流的HUPM算法局限性之一在于算法只能挖掘仅含正项的模式。
在现有的HUPM算法中,采用效用列表结构的单阶段算法已被证明是最有效的[16]。但其主要局限性在于创建和维护列表成本非常昂贵,原因是建立了大量的列表,且列表合并操作成本很高。
为了解决以上局限性,本文提出了基于滑动窗口的含负项的HUPM算法(high utility itemsets with negative items from data stream, HND),设计了一种新颖的列表索引结构(list index structure, LIS)来提升算法性能。
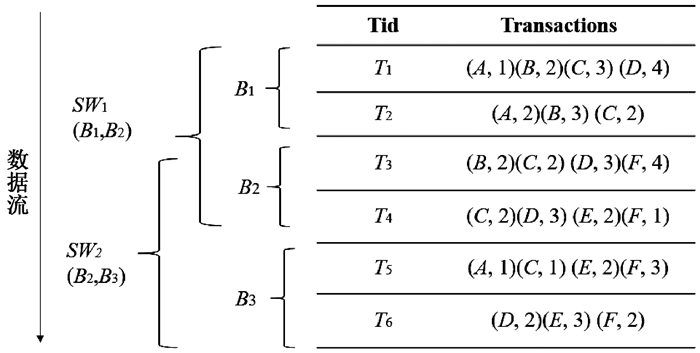
1 基本概念图 1为一个数据流的示例[17],其中每条事务都包含一组项及其数量q,且每个项都有利润值p。如在第一条事务T中包含了四个项,分别是A、B、C、D。示例中,项A到F的利润值分别为1、-1、2、-2、3、-3。项目可能由于亏损出售而带有负效用值,例如项B的利润值为-1。
|
图 1 数据流示意图 Fig. 1 Data flow diagram |
本小节主要介绍在一般HUPM问题中的基本概念和定义。
定义1 项的效用[11]。事务Ti中项z的效用为
| $U(z, {T_i}) = p\left( z \right) \times q(z, {T_i}), $ | (1) |
例如,在示例数据库中,项A在事务T1中的效用为U(A, T1)=p(A)*q(A, T1)=1*1=1。
定义2 项集在事务中的效用[11]。如果项集X⊆Ti,则项集X在事务Ti中的效用为
| $U(X, {T_i}) = \sum\limits_{z \in X} {U(z, {T_i}), } $ | (2) |
例如,在示例数据库中,项集{AB}在T1中的效用为U(AB, T1)=U(A, T1)+U(B, T1)=1+(-2)=-1。
定义3 项集的效用[11]。项集X的效用值计算方法为
| $U(X, {T_i}) = \sum\limits_{{T_i} \in g\left( X \right)} {(X, {T_i}), } $ | (3) |
其中g(X)是包含X的事务集。例如,在示例数据库中,项集{AC}的效用为U(AC, T1)+U(AC, T2)+U(AC, T5)=7+6+3=16。
定义4 事务效用TU[11]。事务Ti的事务效用定义为
| $TU({T_i}) = \sum\limits_{z \in {T_i}} {(z, {T_i}), } $ | (4) |
例如,在示例数据库中,事务T3的事务效用为TU(T3)=U(B, T3)+U(C, T3)+U(D, T3)+U(F, T3)=(-2)+4+(-6)+(-12)=-16。
定义5 事务加权效用TWU[11]。项集X的TWU定义为
| $TWU\left( X \right) = \sum\limits_{X \in {T_j} \wedge {T_j} \in D} {TU({T_j}), } $ | (5) |
例如,在示例数据库中,项目A的事务加权效用为TWU(A)=TU(T1)+TU(T2)+TU(T5)。
定义6 高效用项集[11]。如果U(X)≥minutil,则项目集X是高效用项集;否则,X是低效用项集。
1.2 负项相关定义为了能正确处理负项而不丢失某些可能的结果集,重新定义了事务效用和事务加权效用。
定义7 重新定义的事务效用RTU[11]。事务Τc重新定义的事务效用RTU计算公式为
| $RTU({T_c}) = \sum\limits_{x \subseteq {T_c} \wedge p\left( x \right) > 0} {U(x, {T_c}), } $ | (6) |
例如,在示例数据库中,事务T1重新定义的事务效用为RTU(T1)=U(A, T1)+U(C, T1)=1+6=7。
定义8 重新定义的事务加权效用RTWU[11]。项集X的重新定义的事务加权效用值(RTWU)定义为
| $RTWU({T_c}) = \sum\limits_{X \subset {T_j} \in D} {RTU({T_j}), } $ | (7) |
例如,在示例数据库中,RTWU(A)=RTU(T1)+RTU(T2)+RTU(T5)。
1.3 数据流相关定义定义9 批次总效用[17]。滑动窗口SWk中,批次总效用计算公式为
| $BTU({B_i}) = \sum\limits_{{T_r} \in {B_i}} {TU({T_r}), } $ | (8) |
例如,在示例数据库中,批次B1的总效用值为TU(T1)+TU(T2)。
定义10 滑动窗口总效用[17]。滑动窗口SWk的总效用计算公式为
| $TotalUtility(S{W_k}) = \sum\limits_{{B_j} \in S{W_k}} {BTU({B_j}), } $ | (9) |
例如滑动窗口SW1的总效用值为BTU(B1)+BTU(B2)。
在滑动窗口中处理负项时,为了避免错误地剪枝掉某些模式,重新定义了以上概念。
定义11 重新定义的批次总效用。重新定义某个批次的效用值计算公式为
| $BRTU({B_i}) = \sum\limits_{{T_r} \in {B_i}} {RTU({T_r}), } $ | (10) |
例如,批次B2重新定义的总效用值为RTU(T3)+RTU(T4)。
定义12 重新定义的滑动窗口总效用。滑动窗口SWk的效用计算公式为
| $RTotalUtility(S{W_k}) = \sum\limits_{{B_j} \in S{W_k}} {BRTU({B_j}), } $ | (11) |
例如,在示例数据库中,重新定义后的SW2的窗口总效用为BRTU(B2)+BRTU(B3)。
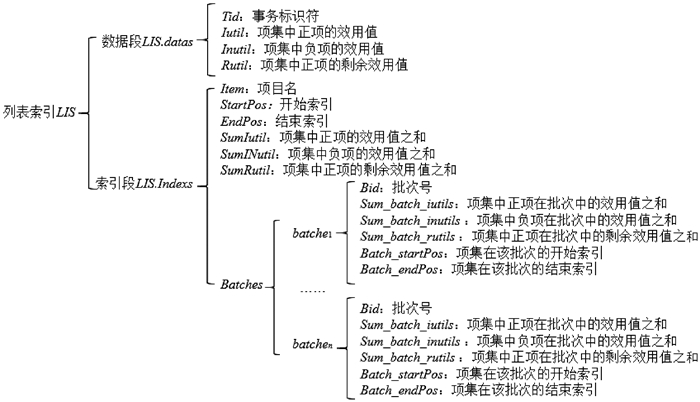
2 HND算法 2.1 列表索引结构LIS旨在快速访问存储在列表中的信息并有效地管理用于存储列表的内存,该结构的框架及存储内容如图 2所示。LIS.datas包含了传统列表中所包含的信息,通过读取LIS.Indexs中从StartPos到EndPos位置的值来快速访问,而batches指示了项目在当前窗口中各批次的信息,当窗口滑动时可快速更新项目信息。
|
图 2 LIS框架图 Fig. 2 LIS frame diagram |
为了减少内存占用,算法应用了内存重用策略。
定义13 内存重用策略[16]。当项集被标识为不是HUIs或无须被扩展时,数据段元组将会重新被用于存储下一个候选项集的信息。
2.2 修剪策略算法在挖掘过程中使用3种修剪策略。
策略1 TWU修剪。令X为项集,如果TWU(X)<minutil,则项集X及其所有超集都是低效用项集。
策略2 使用LIS修剪搜索空间。令X为项集,如果LIS.Indexs (X)中SumIutil和SumRutil值的总和小于minutil,则X及其扩展都是低效用项集。
策略3 令X和Y为项集,如果在EUCS中,Y⊆X,且TWU(Y)<minutil,则X不是HUI,其子集也都不是HUI。
2.3 算法描述算法1为HND算法的主要伪代码,其中:Batch Bi代表新批次;Batch Bold代表当前窗口中最旧的批次;WinSize代表窗口大小;CurrentBatch为窗口中现有批次数;number_of_batches表示批次大小。
算法1 HND
输入:Batch Bi,Batch Bold,winSize,number_of_ batches,LIS,SWi,minutil
输出:the set of high utility itemsets
1) When CurrentBatch=winSize then
2) Scan current window SWi
3) If SWi not the first sliding window then
4) Remove(Bold)
5) Update the RTWU of items
6) Update the LIS and I*
7) Else
8) Initialize LIS
9) Compute RTWU
10) Let I* be the list of single items i
11 End if
12) Let
13) Sort Tk in RTWU ascending order
14) Scan Batch Bi again to build (or update) LIS of items i∈I* and and build EUCS
15) LISMining(
算法的主要步骤如下。
步骤1 算法接收到一批新的事务后,会首先判断当前窗口是否已满(算法1的第1~2行),当满足条件时扫描窗口中事务。
步骤2 窗口已满时,首先判断算法是否正在处理第一批事务,如果是,则计算当前批次中不同项的RTWU并初始化LIS(算法1的第7~10行);否则,将为当前批次更新项的RTWU,并删除最旧批次信息(算法1的第3~6行)。
算法逐批维护项的批次RTWU,以便在新批到达、并删除最旧批时可以轻松地更新项的RTWU;算法计算每个项的RTWU,并以RTWU值的升序建立项目的总顺序
步骤3 第二次数据库扫描,根据
步骤4 调用递归挖掘过程LISMining,开始对项目集进行递归搜索,挖掘过程伪代码如算法2所示。
步骤5 在挖掘过程中,首先计算SumIutils与SumINutils之和是否不小于minutil,如果是,则输出为HUIs(算法2的2~3行)。接着判断索引段中SumIutils与SumRutils之和是否不小于minutil,若是,则继续扩展并递归地挖掘HUIs(算法2的4~11行)。
步骤6 新批次到来,窗口发生滑动,移除旧批次信息并更新LIS中的信息(算法1的第3~6行)。
算法2 LISMining
输入: itemP,ExtensionsOfP,minutil,EUCS,LIS
输出: The set of high utility itemset
1) For each itemset Px∈tensionsOfP do
2) If SumIutils+SumINutils≥minutil then
3) Output Px
4) If (SumIutils+SumRutils) ≥minutil then
5) ExtensionsOfPx←
6) For each itemset Py∈ExtensionsOfP such that y
7) If (
8) Pxy←Px∪Py
9) Pxy←Construct(P, Px, Py)
10) ExtensionOfPx←ExtensionOfPx∪Pxy
11) End If
12) End for
13) LISMining(Px, ExtensionOfPx, minutil, EUCS, LIS)
14) End If
15) End for
2.4 举例说明为了演示利用列表索引结构在数据流中挖掘含负项HUIs的过程,本节将举例说明,将以图 1所示的数据库为示例,并假设用户定义的最小效用阈值minutil=5,Winsize=2,number_of_batches=2。
步骤1 判断当前窗口是否已满,当窗口大小等于现有批次数时,开始扫描窗口。
步骤2 扫描滑动窗口SW1,经判断当前窗口为第一个窗口,且项A到F的RTWU分别为13、17、27、21、10、14,则当前窗口中的总项目顺序为E
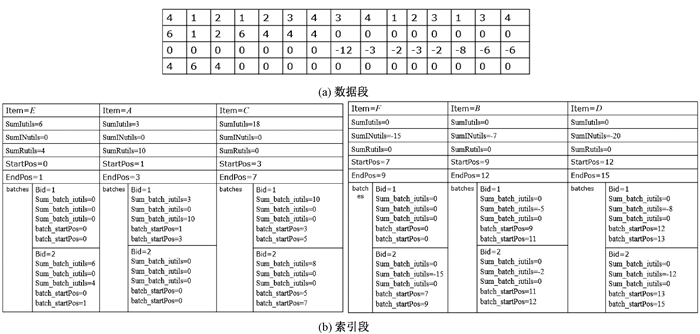
步骤3 依据总顺序再次扫描数据,并重新对数据库中的事务排序,同时构建LIS结构。如图 3所示为SW1中的LIS结构。LIS中数据段存储了项目的效用信息,索引段中则存储了项目的剪枝信息以及项目在数据段中的索引位置。例如通过A的索引值信息可得知A只出现在第一批次中,通过将SumIutil和SumINutil相加可知A不是HUIs,接着计算SumIutil和SumRutil之和,可知A可以被继续扩展。当需要项目A的数据信息时,只需要找到项目A的StartPos以及EndPos即可。在本示例中,项目A的索引为1~3,对应的数据段为{1, 1, 0, 6},{2, 2, 0, 4}。
|
图 3 SW1中构建的LIS结构 Fig. 3 LIS structure built in SW1 |
步骤4 发生挖掘请求时,算法开始递归挖掘HUIs。
步骤5 算法首先判断当前项集是否为高效用项集,例如对于项目A来说,SumIutils+SumInutils<minutil,则A不是高效用项集;但SumIutils+SumRutils>minutil,可以通过扩展A项目寻找HUIs。在挖掘过程中使用LIS比使用传统效用的优势为:当使用传统效用列表合并项集时,需要在内存中逐个或二分查找相应项目的效用列表;合并完项集之后,即使算法判定项集不需要继续扩展时,传统的效用列表也会把它保留在内存当中。而使用LIS执行项集合并时,首先会查找相应项目的索引,从而快速找到项目对应的数据段;当算法判定项集及其超集不可能是HUIs时,LIS会将数据段的空间重新用于存储下一个候选项集的信息。
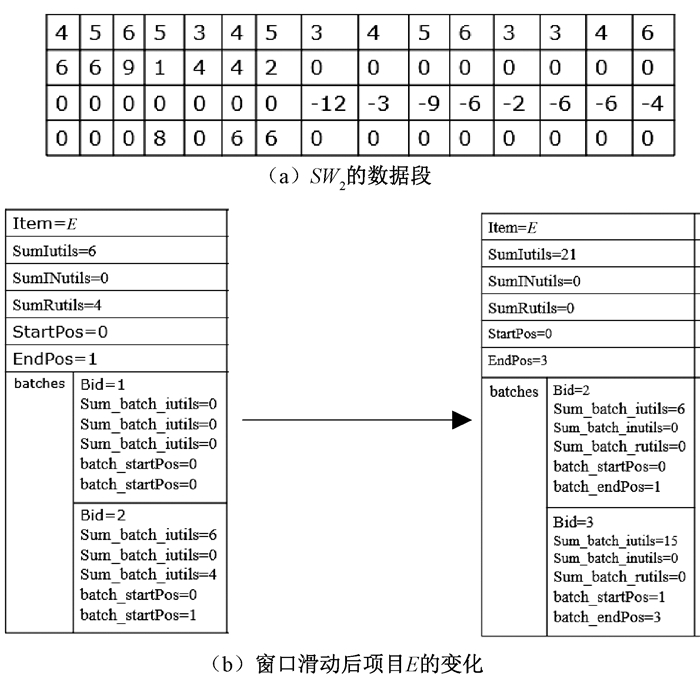
步骤6 新的批次到来,LIS结构相应的更新。图 4(a)为窗口发生滑动后LIS的数据段,最旧批次即第一批次的数据段已被删除,同时更新了索引段中的索引值;当数据插入时,将插入到项目的结束索引之后,并更新之后项目的索引值。图 4(b)为滑动窗口后项目E的变化,E在批次一中没有数据,因此不需要删除,当插入新批次时,算法先找到E的结束索引1,并在该位置插入新批次中的数据{5, 6, 0, 0},{6, 9, 0, 0},同时更新索引值,其他项目则按照此步骤依次更新。
|
图 4 窗口滑动后的LIS Fig. 4 LIS after deleting window sliding |
为了测试HND算法的性能,本文做了大量的实验,实验运行环境的CPU为3.00 GHz,内存为256 GB,操作平台是Win10企业版。实验使用四个真实数据集mushroom、chess、retail和kosarak,所有数据集均从spmf[18]上下载,每个数据集均包含带负效用的项,表 1显示了实验中使用数据集的基本特征。我们为数据集设置不同minutil,其代表高效用项集必须满足的“重要性”下界,用“重要性”作为minutil的单位。
|
|
表 1 数据集基本特征 Tab. 1 Basic characteristics of the data set |
HND算法是第一个在数据流中挖掘含负项的HUPM算法,因此找不到相同性能的另一算法进行比较,而评估其性能的可靠方法是将其与静态或增量算法中现有的可以挖掘含负项HUIs的算法相比。
迄今为止,现有的可以挖掘含负项的HUIs算法都针对静态数据库。经查阅文献可知,Li等[19]提出的EHIN算法为现有的挖掘含负项最先进的HUPM算法之一,为了减少数据集扫描,EHIN使用事务合并和数据集投影技术。FHN[20]也是挖掘含负项HUIs的算法。增量数据库中则没有可以挖掘含负项HUIs的算法,为此,本文在增量算法EIHI[21]中进行了进一步改进,在不改变数据结构和关键技术的基础上,将其改进为可以同时处理含正项和负项的HUPM算法。在对比实验中,依据算法的插入率不同,将算法命名为EIHI-n-5和EIHI-n-10,即分别将数据集分5个批次、10个批次增量输入算法中。为了可以与静态和增量中的相关算法作对比,本算法在单窗口中以不同的批次数进行实验。实验中,设置了所提出算法的不同版本HND-5以及HND-10,分别表示算法在单窗口中以5批次、10批次增量插入。同时,为了测试LIS结构的有效性,还设置了所提出算法的“静态”版本,即在单窗口中以一个批次运行,在本实验中,称此版本为HND-1。
3.2 执行时间性能本小节评估了所有算法在数据集中的运行时间性能,EIHI-n-5和EIHI-n-10的执行时间在有些图中无法画出来,因为它需要更多的执行时间和内存。
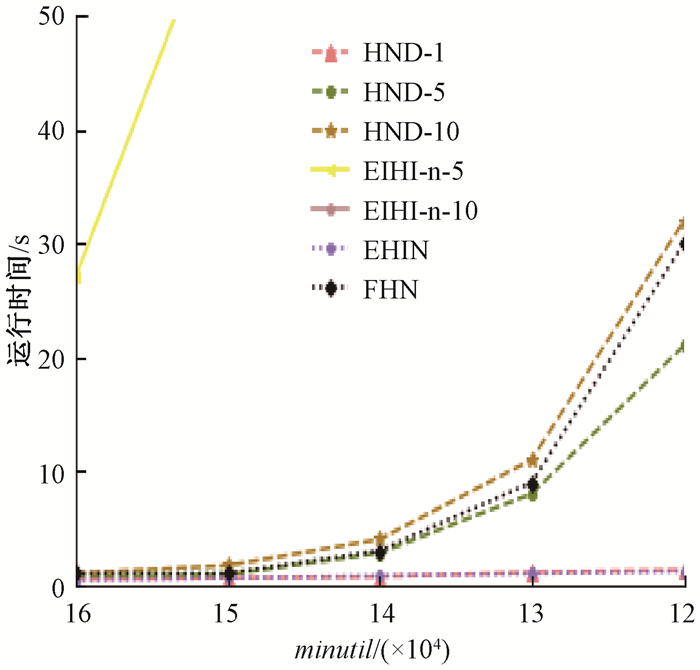
如图 5所示,在密集数据集chess中,几乎在所有不同的阈值下,HND-1和EHIN的运行时间都所差无几,而当minutil值大于150 000重要性时,FHN的运行时间要明显大于HND-1的运行时间;增量处理数据集时,运行时间都会随着minutil的增加而增加,并且批次数越多,运行时间越长。HND的多批次运行算法在chess数据集上表现出了比EIHI更加优异的性能,并且批次数越多,效果越明显,运行时间提高了28倍。
|
图 5 算法在chess上的运行时间 Fig. 5 The running time of the algorithm on chess |
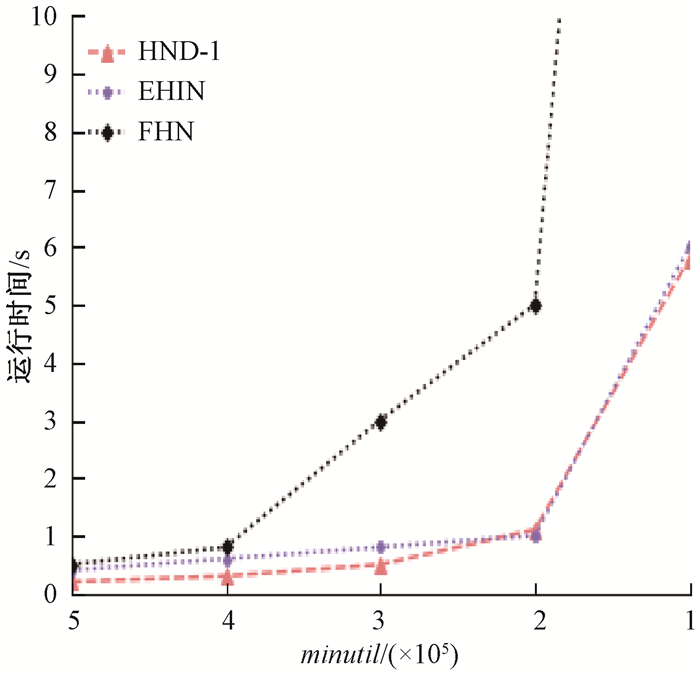
在密集数据集mushroom中,静态与动态算法运行时间相差较多,所以分为了图 6和图 7来展示实验结果。图 6为静态算法的运行时间,当minutil的值在500 000重要性和200 000重要性时,HND-1的运行时间要少于EHIN,由于mushroom和chess相比,事务的平均长度较短,所以运行时间的差异较小,但依然能证明HND所使用结构的有效性。之后,当minutil逐步增加时,EHIN和HND-1有着几乎相同的运行时间,而在各种阈值下,FHN的算法都需要更多的运行时间。
|
图 6 Mushroom上的静态算法运行时间 Fig. 6 Running time of static algorithm on mushroom |
|
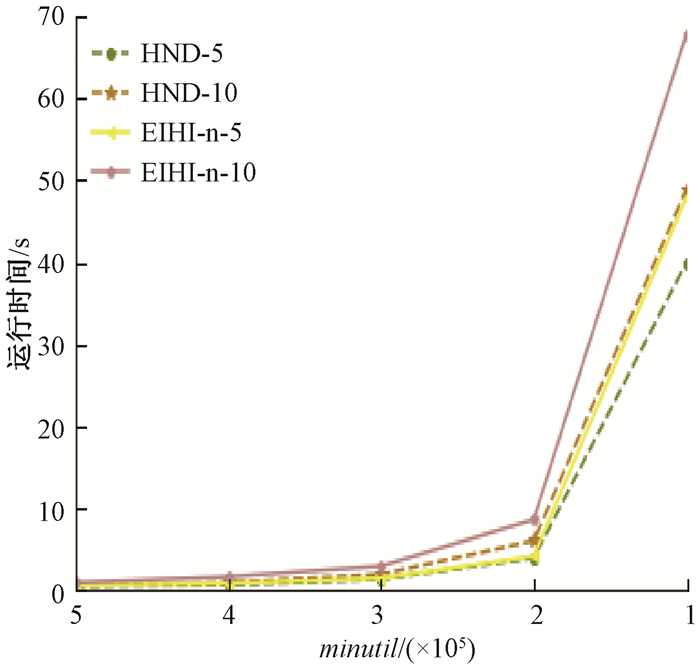
图 7 Mushroom上的增量算法运行时间 Fig. 7 Running time of incremental algorithm on mushroom |
在mushroom数据集上的动态运行算法中,算法的运行时间都会随着minutil的增加而增加,并且批次数越多,运行时间越长。HND-n-5在mushroom上使用最少的时间,而EIHI-n-5和HND-n-10的运行时间较为接近,说明在增量处理密集数据集时,HND所提出的数据结构依旧可以有效地减少运行时间,如图 7所示。
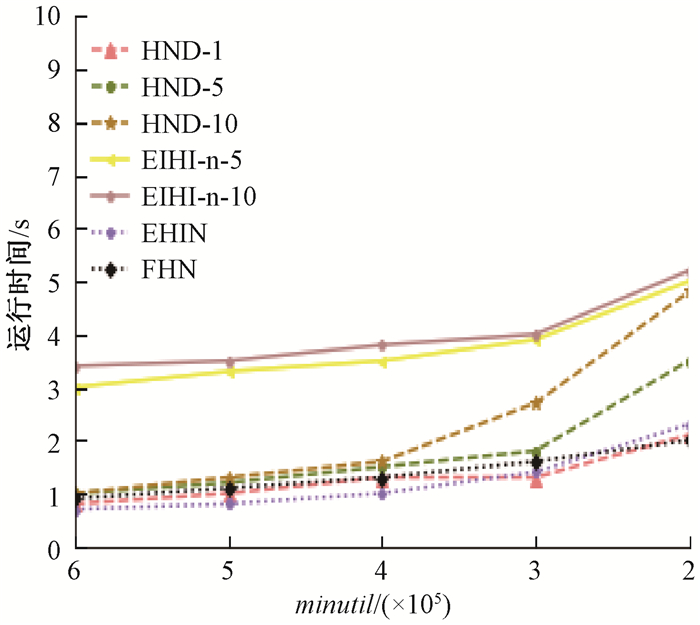
图 8为算法在稀疏数据集retail上的运行时间,三种静态算法运行时间几乎相同,而在增量处理数据集时,HND则比EIHI表现出了更好的性能,minutil越大,效果则越明显。
|
图 8 算法在retail上的运行时间 Fig. 8 The running time of the algorithm on retail |
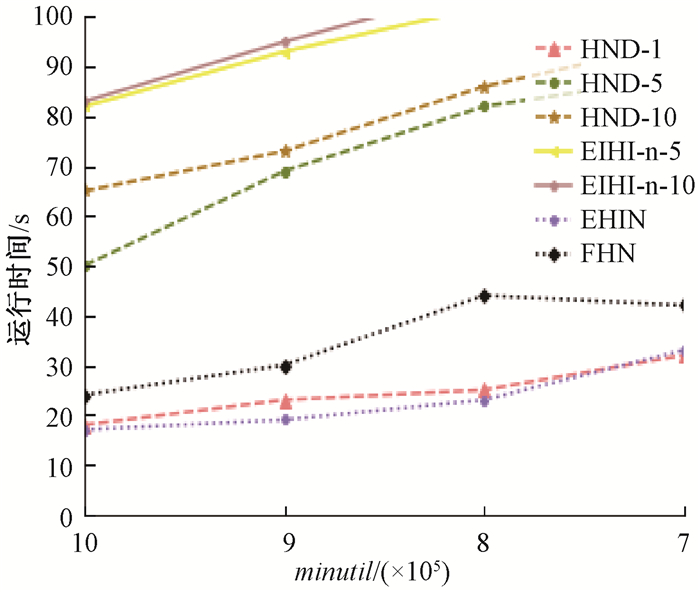
在kosarak数据集中,算法的运行时间如图 9所示。EHIN和HND使用几乎相同的运行时间,EHIN采用了数据库投影策略,可以大大减少扫描的范围,而HND则单独使用索引结构来加快挖掘速度,从一定程度上也说明HND所提出的LIS结构是有效的。在增量挖掘HUIs的算法中,HND算法的运行时间始终要优于EIHI算法,也说明了在增量挖掘的过程中,LIS结构显示出了优异的性能。
|
图 9 算法在kosarak上的运行时间 Fig. 9 The running time of the algorithm on kosarak |
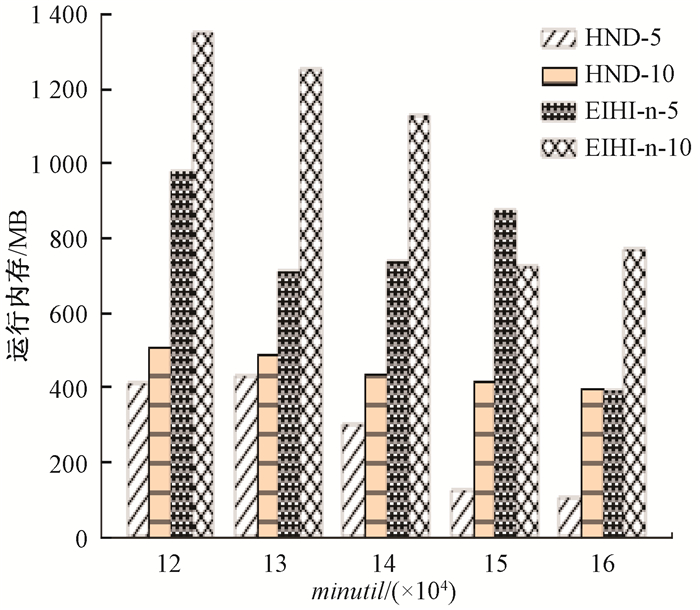
由于分批次处理数据集会在一定程度上占用比静态算法更多的内存,因此,本节比较了增量算法EIHI与HND在各种数据集上的内存占用。图 10~13展示了HND算法和对比算法在所有数据集的运行内存情况。
|
图 10 算法在chess上的内存消耗 Fig. 10 The memory consumption of the algorithm on chess |
|
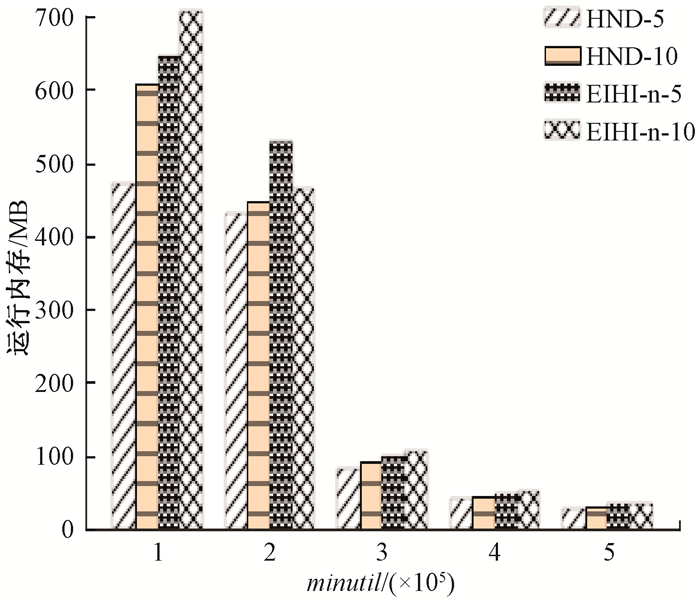
图 11 算法在mushroom上的内存消耗 Fig. 11 The memory consumption of the algorithm on mushroom |
|
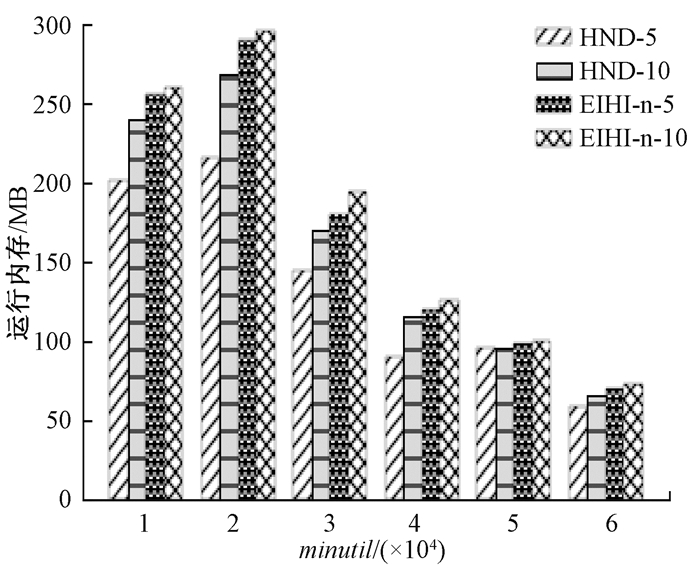
图 12 算法在retail上的内存消耗 Fig. 12 The memory consumption of the algorithm on retail |
|
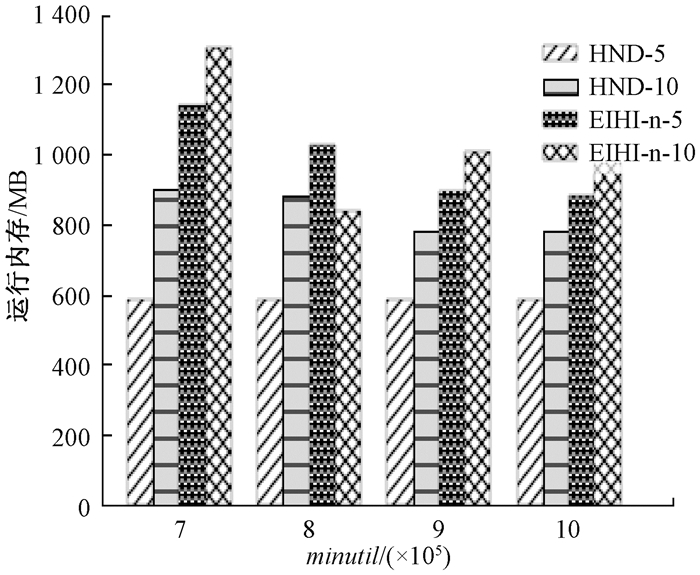
图 13 算法在kosarak上的内存消耗 Fig. 13 The memory consumption of the algorithm on kosarak |
图 10为算法在chess数据集中的内存消耗,随着批次数的增加,算法消耗的内存也逐步增加,但HND的算法依旧比EIHI算法要表现出更好的性能。
算法在mushroom中的内存消耗如图 11所示,当minutil足够大时,EIHI和HND在挖掘过程中的内存占用相差不大,但是当minutil逐渐减少时,EIHI和HND的内存占用差异逐步增大,且HND要占用更少的内存。原因是当minutil减少时,候选项集数量增多,而这个时候则更能体现出列表索引结构的优点。
在retail数据集上,算法都随着批次数的增加而消耗更多的内存,同样,随着minutil的减少,算法也会占用更多的内存。而在所有条件下,HND算法表现最优,证明在稀疏数据集中,HND也可以很好地减少内存占用,如图 12所示。
在kosarak数据集中,算法的内存占用与retail数据集上的结果类似,不同的是,HND的优势体现得更加明显,因为在kosarak数据集中,项的个数要更多,因此HND的性能会更好,如图 13所示。
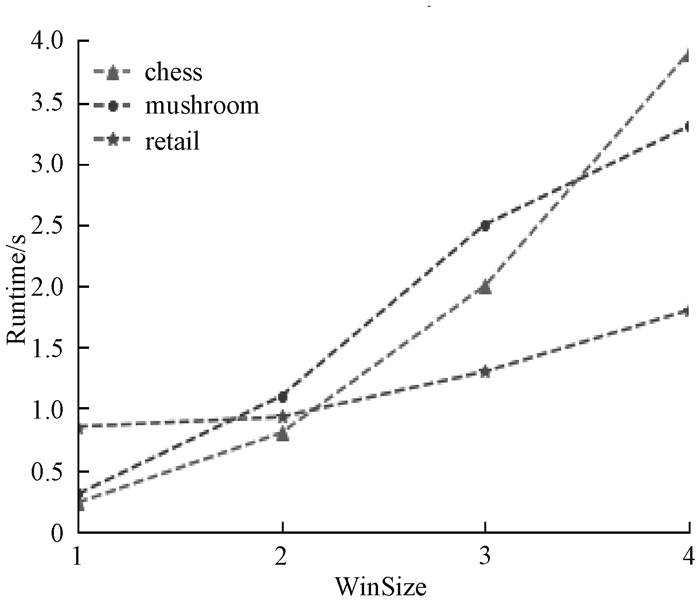
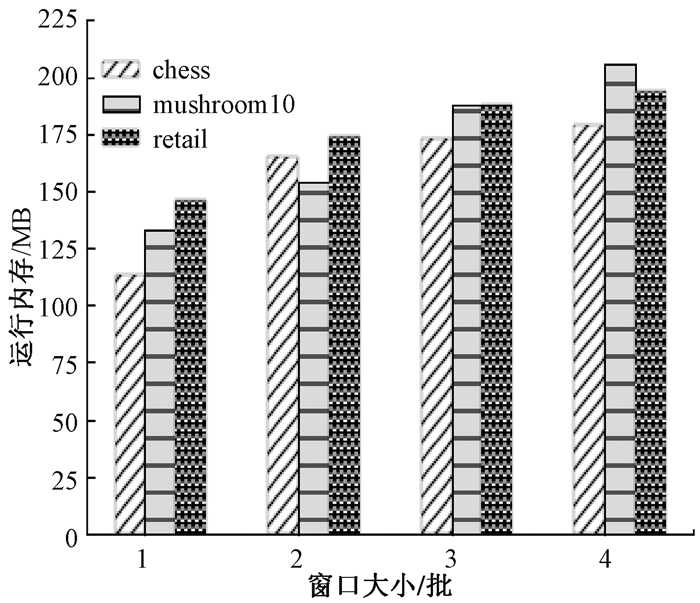
3.4 滑动窗口的影响在基于滑动窗口的模式挖掘算法中,窗口大小是一个非常重要的参数,本节比较了在不同窗口大小下HND算法的运行性能。图 14和图 15分别显示了窗口大小对运行时间和内存的影响。图中只展示了算法在chess、mushroom以及retail数据集中的运行性能,因在kosarak中需要更多的时间及空间。随着窗口逐渐变大,即一个窗口中包含的批次数增多,运行时间和内存消耗都逐渐升高。整体来说算法在chess数据集中使用最小的时间和空间。
|
图 14 窗口大小对运行时间的影响 Fig. 14 The effect of window size on runtime |
|
图 15 窗口大小对运行内存的影响 Fig. 15 The effect of window size on running memory |
对于运行时间来说,EHIN和HND-1的性能不相上下,但本文所提出算法旨在动态数据库数据流中挖掘HUIs,所提出列表索引结构在有事务增删时会表现出更好的性能,而EHIN则不能处理事务的增删。就数据结构的有效性来说,HND只使用了列表索引结构来加快挖掘速度,而EHIN使用的投影数据库策略和事务合并技术,从一定程度上也证明了本文所提出结构可以在挖掘过程中大大减少运行时间。算法增量处理数据集时,所表现出的性能也大大优于EIHI算法,证明所提出结构在处理动态数据集时也表现出优异的性能。
对于内存消耗来说,与EIHI算法对比,HND算法表现出了更好的性能,在所有数据集中,HND都比EIHI算法占用更少的内存,同时也证明了所提出算法可以明显地减少内存占用。
4 总结首先,针对现有的基于效用列表的算法在合并列表时成本较高的问题,提出了列表索引结构LIS,依据LIS中的索引值可以快速访问并更新存储在数据段中的项目信息,从而达到加快挖掘速度并减少内存消耗的目的。其次,基于LIS提出了第一种在数据流中挖掘含负项的HUPM算法,在滑动窗口时利用LIS所存储的项集的正负效用值信息挖掘含负项的HUIs,解决了之前在数据流中只能处理正项的问题。进行了广泛的实验评估,结果表明所提出算法无论是在运行时间还是内存消耗上,在密集和稀疏数据集上都表现良好。但是就算法研究来说,仅使用LIS结构来提高效率是不足的,还需要加入新颖的剪枝策略或技术来进一步优化算法。
| [1] |
ALMOQBILY R S, RAUF A, QURADAA F H. A survey of correlated high utility pattern mining[J]. IEEE access, 2021, 9: 42786-42800. DOI:10.1109/ACCESS.2021.3065393 (  0) 0) |
| [2] |
LIU J Q, JU X Y, ZHANG X X, et al. Incremental mining of high utility patterns in one phase by absence and legacy-based pruning[J]. IEEE access, 2019, 7: 74168-74180. DOI:10.1109/ACCESS.2019.2919524 (  0) 0) |
| [3] |
YUN U, NAM H, LEE G, et al. Efficient approach for incremental high utility pattern mining with indexed list structure[J]. Future generation computer systems, 2019, 95: 221-239. DOI:10.1016/j.future.2018.12.029 (  0) 0) |
| [4] |
LEE J, YUN U, LEE G, et al. Efficient incremental high utility pattern mining based on pre-large concept[J]. Engineering applications of artificial intelligence, 2018, 72: 111-123. DOI:10.1016/j.engappai.2018.03.020 (  0) 0) |
| [5] |
LAN G C, HONG T P, HUANG J P, et al. On-shelf utility mining with negative item values[J]. Expert systems with applications, 2014, 41(7): 3450-3459. DOI:10.1016/j.eswa.2013.10.049 (  0) 0) |
| [6] |
LAN G C, HONG T P, TSENG V S. Discovery of high utility itemsets from on-shelf time periods of products[J]. Expert systems with applications, 2011, 38(5): 5851-5857. DOI:10.1016/j.eswa.2010.11.040 (  0) 0) |
| [7] |
DAM T L, LI K L, FOURNIER-VIGER P, et al. An efficient algorithm for mining top-k on-shelf high utility itemsets[J]. Knowledge and information systems, 2017, 52(3): 621-655. DOI:10.1007/s10115-016-1020-2 (  0) 0) |
| [8] |
KIM H, YUN U, BAEK Y, et al. Efficient list based mining of high average utility patterns with maximum average pruning strategies[J]. Information sciences, 2021, 543: 85-105. DOI:10.1016/j.ins.2020.07.043 (  0) 0) |
| [9] |
SETHI K K, RAMESH D. High average-utility itemset mining with multiple minimum utility threshold: a generalized approach[J]. Engineering applications of artificial intelligence, 2020, 96: 103933. DOI:10.1016/j.engappai.2020.103933 (  0) 0) |
| [10] |
KIM J, YUN U, YOON E, et al. One scan based high average-utility pattern mining in static and dynamic databases[J]. Future generation computer systems, 2020, 111: 143-158. DOI:10.1016/j.future.2020.04.027 (  0) 0) |
| [11] |
HAN X X, LIU X M, LI J Z, et al. Efficient top-k high utility itemset mining on massive data[J]. Information sciences, 2021, 557: 382-406. DOI:10.1016/j.ins.2020.08.028 (  0) 0) |
| [12] |
SINGH K, SINGH S S, KUMAR A, et al. TKEH: an efficient algorithm for mining top-k high utility itemsets[J]. Applied intelligence, 2019, 49(3): 1078-1097. DOI:10.1007/s10489-018-1316-x (  0) 0) |
| [13] |
KRISHNAMOORTHY S. Mining top-k high utility itemsets with effective threshold raising strategies[J]. Expert systems with applications, 2019, 117: 148-165. DOI:10.1016/j.eswa.2018.09.051 (  0) 0) |
| [14] |
SUN R, HAN M, ZHANG C Y, et al. Mining of top-k high utility itemsets with negative utility[J]. Journal of intelligent & fuzzy systems, 2021, 40(3): 5637-5652. (  0) 0) |
| [15] |
YILDIRIM I, CELIK M. Mining high-average utility itemsets with positive and negative external utilities[J]. New generation computing, 2020, 38(1): 153-186. DOI:10.1007/s00354-019-00078-8 (  0) 0) |
| [16] |
DUONG Q H, FOURNIER-VIGER P, RAMAMPIARO H, et al. Efficient high utility itemset mining using buffered utility-lists[J]. Applied intelligence, 2018, 48(7): 1859-1877. DOI:10.1007/s10489-017-1057-2 (  0) 0) |
| [17] |
程浩东, 韩萌, 张妮, 等. 基于滑动窗口模型的数据流闭合高效用项集挖掘[J]. 计算机研究与发展, 2021, 58(11): 2500-2514. CHENG H D, HAN M, ZHANG N, et al. Closed high utility itemsets mining over data stream based on sliding window model[J]. Journal of computer research and development, 2021, 58(11): 2500-2514. DOI:10.7544/issn1000-1239.2021.20200554 (  0) 0) |
| [18] |
FOURNIER-VIGER P, GOMARIZ A, GUENICHE T, et al. SPMF: A Java open-source pattern mining library[J]. Journal of machine learning research, 2014, 15(1): 3389-3393. (  0) 0) |
| [19] |
LI H F, HUANG H Y, LEE S Y. Fast and memory efficient mining of high-utility itemsets from data streams: with and without negative item profits[J]. Knowledge and information systems, 2011, 28(3): 495-522. DOI:10.1007/s10115-010-0330-z (  0) 0) |
| [20] |
LIN J C W, FOURNIER-VIGER P, GAN W S. FHN: an efficient algorithm for mining high-utility itemsets with negative unit profits[J]. Knowledge-based systems, 2016, 111: 283-298. DOI:10.1016/j.knosys.2016.08.022 (  0) 0) |
| [21] |
FOURNIER-VIGER P, LIN C W, GUENICHE T, et al. Efficient incremental high utility itemset mining[EB/OL]. [2021-01-10]. https://dl.acm.org/doi/pdf/10.1145/2818869.2818887.
(  0) 0) |
 2022, Vol. 54
2022, Vol. 54


