0 引言

模型检测(model checking)^[1]作为一种高效的形式化验证方法，由于其自动验证的优点，广泛应用于计算机软硬件的正确性与安全性验证^[2-5]。模型检测技术的基本思想是将现实中的系统抽象为状态迁移系统模型，通过特定的时序逻辑^[6-7]描述系统的性质，例如计算树逻辑(computation tree logic, CTL)^[8-10]，并采用对应的模型检测算法验证系统模型是否满足相应的性质。若满足，验证通过；若不满足，则给出反例。传统的模型检测方法起初是为了验证系统中定性属性而设计的，例如安全性与活性。然而，许多复杂的系统具有随机性、非可加性等定量特征^[11-12]，无法通过经典模型检测方法验证。因此，定量的模型检测方法引起了学术界与工业界的重视。

在模糊理论基础上，将可能性测度理论^[13]与模型检测方法结合，文献[14-18]提出了可能性计算树逻辑模型检测方法。该方法以可能性Kripke结构或广义可能性Kripke结构作为系统模型，两种模型的主要区别是可能性Kripke结构要求状态转移关系中必须存在可能性为1的转移，而广义可能性Kripke结构则不要求。在此基础上，我们提出了基于决策过程的广义可能性计算树逻辑模型检测方法^[15]，主要用于具有非确定性与信息不完备性系统的验证。该方法的主要特点是引入了决策过程，以广义可能性决策过程作为模型(generalized possibilistic decision processes, GPDP)^[16]，广义可能性计算树逻辑(generalized possibilistic CTL, GPoCTL)^[17-18]描述系统的性质，最终通过算法将模型检测问题^[19-21]转换为复杂度较低的模糊矩阵合成运算。

在实际的系统设计中，系统产生的成本开销、能耗^[22]等也是我们需要重视的问题。例如，在医疗专家系统中，除治疗效果外，我们还关心每种治疗方案所产生的费用，从而能够选取性价比最高的诊疗方案。在工程管理中，要考虑到花费的人力资源、财力、时间成本等诸多因素，并综合分析出最优方案^[23]。广义可能性决策过程模型虽然能够对具有不完备信息的非确定性系统进行建模，但无法刻画这类系统所产生的成本开销、能耗等量化特征。为解决此类问题，我们在广义可能性决策过程模型的基础上增加了成本约束，在进行动作的非确定选择时会产生相应的成本开销，从而能够对系统的实际成本进行分析，丰富了GPoCTL模型检测的应用场景。

针对需要考虑成本开销的非确定系统，本文首先引入带成本的广义可能性决策过程模型，接着给出此模型下GPoCTL的语法及语义，最后研究带成本的GPoCTL模型检测算法。此外，我们还将给出此模型在病人诊疗专家系统中的应用。

1 预备知识

本文用到了一些模糊数学的运算符号，下面给出其定义。

定义1^[21]  设X为普通集合，集合X上模糊集合满足映射A: X→[0, 1], A也称为模糊集合A的隶属度函数，对x∈X, A(x)称为x属于模糊集A的隶属度。

用F(X)表示X上模糊集合的全体，即F(X)={A|A: X→[0, 1]}。

定义2^[21]  设A, B∈F(X)，A与B的并A∪B、交A∩B、补A^c的隶属函数定义为

$ (A \cup B)(x)=A(x) \vee B(x)=\max \{A(x), B(x)\}, $

$ (A \cap B)(x)=A(x) \wedge B(x)=\min \{A(x), B(x)\}, $

$ A^{c}(x)=1-A(x) 。$

本文是对广义可能性决策过程进行扩展得到带成本的广义可能性决策过程，下面给出广义可能性决策过程的定义。

定义3^[15]  广义可能性决策过程(generalized possibilistic decision processes, GPDPs)由六元组M=(S, Act, p, I, AP, L)定义，其中：

1) S是可数非空状态集合;

2) Act是动作集;

3) p: S×Act×S→[0, 1]是可能性转移分布，对于任意s∈S, α∈Act，存在状态t∈S，使P(s, α, t)>0;

4) I: S→[0, 1]是可能性初始分布函数;

5) AP是原子命题集合;

6) L: S×AP→[0, 1]是标签函数，L(s, a)表示原子命题a在状态s上成立的真值。

2 带成本的广义可能性决策过程

对GPDP六元组进行扩展，增加成本函数，从而得到带成本的广义可能性决策过程，其形式化定义如下。

定义4  带成本的广义可能性决策过程(generalized possibilistic decision processes with costs, CGPDP)是一个七元组M_c=(S, Act, p, I, AP, L, C)，其中：

1) S是可数非空状态集合;

2) Act是动作集;

3) p: S×Act×S→[0, 1]是可能性转移分布，对于任意s∈S, α∈Act，存在状态t∈S，使P(s, α, t)>0;

4) I: S→[0, 1]是可能性初始分布函数;

5) AP是原子命题集合;

6) L: S×AP→[0, 1]是标签函数，L(s, a)表示原子命题a在状态s上成立的真值。

7) C: S×Act→N(N为自然数集)是成本函数，对于任意s∈S, α∈Act，产生成本C(s, α)。

若动作集与原子命题集均有穷，则称M_c为有穷CGPDP。若存在一状态t∈S，使得p(s, α, t)>0，则称α在状态s上是可激活的，Act(s)表示s所有可激活的动作集合。

用$\hat{\pi}$=s₀α₀s₁α₁s₂…s_n-1α_n-1s_n表示M_c中一条有穷路径，π=s₀α₀s₁α₁s₂…∈(S×Act)^ω表示M_c中的一条无穷路径。从状态s出发的路径集合用Paths(s)表示。Paths^fin(M_c)表示M_c中所有状态出发的有穷路径集合，Paths(M_c)表示M_c中所有状态出发的无穷路径集合。

对于π=s₀α₀s₁α₁s₂…∈(S×Act)^ω，通过有穷路径$\hat{\pi}$↓_n=s₀α₀s₁α₁s₂…s_n-1α_n-1s_n表示以s_n结尾的有穷前缀，以无穷路径π↑ⁿ=s_nα_ns_n+1α_n+1s_n+2α_n+2…∈(S×Act)^ω表示从s_n开始的路径π的无穷后缀。

对于π=s₀α₀s₁α₁s₂…∈(S×Act)^ω，第k步的瞬时成本为cost[=k](π)=C(s_k-1, α_k-1)，前k步累积成本为cost[≤k](π)=$\sum\limits_{i=1}^{k}$cost[=i](π)。

对于π=s₀α₀s₁α₁s₂…∈(S×Act)^ω，集合F⊆S，当π能够最终访问F中所包含的任意状态时，该路径到达F的累积成本为

$ {cost}[\diamond F](\pi)={cost}[\leqslant n](\pi), $

其中：s_n∈F且s₀, …, s_n-1∉F。

注1  给定集合A、B，A×B表示集合A与B的笛卡尔积。

注2  对任意α∈Act，可通过模糊矩阵表示其可能性转移p：S×α×S→[0, 1]，记为P_α。该矩阵的闭包记为P_α⁺，自反闭包记为P_α^*。

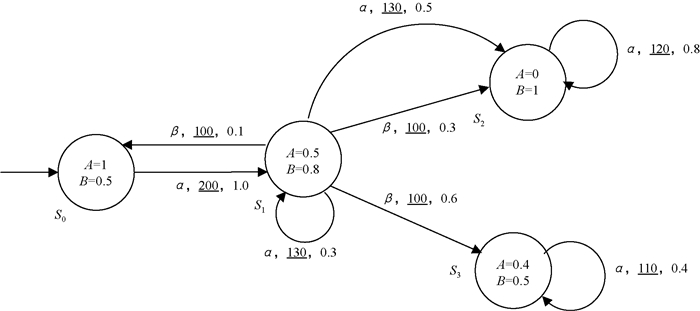
例1  图 1给出了一个4状态的有穷CGPDP模型M_c=(S, Act, p, I, AP, L, C)，圆圈表示状态，带箭头的连接线表示转移，连接线上无下划线的数字表示转移的可能性，带下划线的数字表示转移的成本。如转移${{\mathit{{s}}}_{1}}\xrightarrow{\underline{\alpha, 130, 0.5}}{{\mathit{{s}}}_{2}}$表示状态s₁在动作α作用下，到达状态s₂的成本为130，可能性为0.5，即p(s₁, α, s₂)=0.5，C(s₁, α)=130。而S={s₀, s₁, s₂, s₃}，Act={α, β}，初始分布I与α、β对应的转移矩阵分别为

$ \boldsymbol{P}_{I}=\left(\begin{array}{l} 1 \\ 0 \\ 0 \\ 0 \end{array}\right), \boldsymbol{P}_{\alpha}=\left(\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0.3 & 0.5 & 0 \\ 0 & 0 & 0.8 & 0 \\ 0 & 0 & 0 & 0.4 \end{array}\right), $

$ \boldsymbol{P}_{\beta}=\left(\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0.1 & 0 & 0.3 & 0.6 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right)。$

对于路径π=s₀αs₁βs₂αs₂…，第3步的瞬时成本C(s₂, α)=120，前3步累积成本为

$ \begin{aligned} &{cost}[\leqslant 3](\pi)=C\left(s_{0}, \alpha\right)+C\left(s_{1}, \beta\right)+ \\ &C\left(s_{2}, \alpha\right)=420。\end{aligned} $

对于集合F={s₂, s₃}，π到达F的累积成本为cost[◇F](π)=C(s₀, α)+C(s₁, β)=300。

由例1可以看出，CGPDP中的状态可以选择多个动作。如s₁在转移时可选择动作α或β，这种选择是非确定的。为消除CGPDP中状态对动作的非确定性选择，我们引入调度。

定义5  给定一个有穷的CGPDP M_c=(S, Act, p, I, AP, L, C)，定义函数Adv: S→Act为M_c的调度。对任意s∈S，有Adv(s)∈Act(s)。

在调度Adv下，从状态s出发的路径集合用Paths_Adv(s)表示，Paths_Adv^fin(M_c)表示M_c中所有状态出发的有穷路径集合，Paths_Adv(M_c)表示M_c中所有状态出发的无穷路径集合。

定义6  设M_c=(S, Act, p, I, AP, L, C)是有穷的CGPDP，定义函数r_Adv: S→[0, 1]为

$ \begin{aligned} &r_{A d v}(s)=\bigvee\left\{\bigwedge_{i \geqslant 0} p_{A d v}\left(s_{i}, \alpha_{i+1}, s_{i+1}\right) \mid s_{0}=s,\right. \\ &\left.s_{i} \in S, \alpha_{i} \in A c t\right\}, \end{aligned} $

r_Adv(s)是在调度Adv下，从状态s出发的最大可能性。文献[15]的定理1已经给出了r_Adv(s)的计算过程，此处直接引用。

定理1^[15]  给定有穷的CGPDP M_c，对任意s∈S，有r_Adv(s)=$\bigvee\limits_{t \in S}$(p_Adv⁺(s, t)∧p_Adv⁺(t, t))。

定义7  设M_c=(S, Act, p, I, AP, L, C)是一个有穷的CGPDP，给定一条有穷路径$\hat{\pi}$=s₀α₀s₁α₁s₂…s_n-1α_n-1s_n∈Paths_Adv^fin(M_c)，对应柱集定义为

Cyl($\hat{\pi}$)={π∈Paths_Adv(M_c)$\hat{\pi}$是π的有穷前缀}。

定义8  给定有穷的CGPDPM_c，则函数GPo: Paths_Adv(M_c)→[0, 1]定义为

$ G P o(\pi)=I\left(s_{0}\right) \bigwedge \bigwedge_{i \geqslant 0} p_{A d v}\left(s_{i}, \alpha_{i}, s_{i+1}\right)。$

对于任意集合F⊆Paths_Adv(M_c)，有GPo(F)=∨{GPo(π)|π∈F}，即可扩展为函数GPo: 2^{Paths_Adv(M_c)}→[0, 1]，称为集合2^{Paths_Adv(M_c)}上的广义可能性测度。

3 期望成本

引入调度Adv后，CGPDP中任意状态s在Adv下的转移动作α得以确定。由s出发不断通过Adv确定的动作发生转移，从而产生路径集合Paths_Adv(s)。为定量刻画这些路径所产生的成本，结合广义可能性模型检测中的理论，我们引入了期望成本这一概念。CGPDP中的期望成本主要包括瞬时期望成本、累积期望成本与可达期望成本。

定义9  给定有穷CGPDP M_c，在调度Adv下，Paths_Adv(s)中所有路径在第k步瞬时成本cost[=k]的期望值，称为从s出发第k步的期望成本，递归定义为

若k=1，则

$ E x_{s}^{A d v}({cost}[=1])=\left(\bigvee_{t \in S} p_{A d v}(s, \alpha, t)\right) \cdot C_{A d v}(s, \alpha) ; $

若k>1，则

$ \begin{aligned} &E x_{s}^{A d v}({cost}[=k])=\left(\bigvee_{t \in S} p_{A d v}(s, \alpha, t)\right)\cdot \\ &E x_{t}^{A d v}(cost [=k-1])。\end{aligned} $

对于集合F⊆S，从s出发第k步到达F的期望成本，是Ex_s^Adv(cost[=k])的扩展，

若k=1，则

$ \begin{aligned} &E x_{s}^{A d v}({cost}[=1(\diamond F)])= \\ &\left(\bigvee_{u \in F} p_{A d v}(s, \alpha, u)\right) \cdot C_{A d v}(s, \alpha); \end{aligned} $

若k>1，则

$ \begin{aligned} &E x_{s}^{A d v}({cost}[=k](\diamond F))= \\ &\left(\bigvee_{t \in S^{\prime}} p_{A d v}(s, \alpha, t)\right) \cdot E x_{t}^{A d v}({cost}[=k-1(\diamond F)]), \end{aligned} $

其中：S′={s∈S|GPo(s|=◇F)>0且s∉F}。

定义10  给定有穷CGPDP M_c，在调度Adv下，Paths_Adv(s)中所有路径前k步累积成本cost[≤k]的期望值，称为从s出发前k步的期望累积成本，定义为Ex_s^Adv(cost[≤k])=$\sum\limits_{i=1}^{k}$Ex_s^Adv(cost[=i])。

对于集合F⊆S，从s出发前k步到达F的期望累积成本，是Ex_s^Adv(cost[≤k])的扩展，定义为

$ \begin{aligned} &E x_{s}^{A d v}({cost}[\leqslant k(\diamond F)])= \\ &\sum\limits_{i=1}^{k} E x_{s}^{A d v}({cost}[=i(\diamond F)])。\end{aligned} $

定义11  给定有穷CGPDP M_c，在调度Adv下，从s出发到达F的所有路径的期望累积成本Ex_s^Adv(cost[◇F])定义为

若GPo(s|=◇F)=0，则Ex_s^Adv(cost[◇F])=∞；

若s∈F，则Ex_s^Adv(cost[◇F])=0；

若GPo(s|=◇F)>0且s∉F，则

$ E x_{s}^{A d v}({cost}[\diamond F])=E x_{s}^{A d v}({cost}[\leqslant n(\diamond F)])。$

n是到达F的所有路径长度的最大值。带成本的广义可能性决策过程计算树逻辑模型检测问题首先考虑的是满足公式的可能性，然后再计算期望成本。在计算可能性时，本文使用有穷路径的可能性来计算无穷路径的可能性，故考虑成本时，也只考虑有穷路径的期望成本，即只考虑一次或有限次的自环。

4 带成本广义可能性计算树逻辑

在文献[15]中提出的GPoCTL基础上，增加了公式(=k)、(≤k)、(Φ)。下面给出带成本GPoCTL的语法和语义解释。

定义12(GPoCTL语法)  GPoCTL状态公式定义为

$ \varPhi::= { true }|a| \varPhi_{1} \wedge \varPhi_{2} \mid \neg \varPhi $

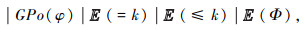
其中：φ是路径公式；a∈AP。(=k)、(≤k)、(Φ)分别表示第k步瞬时期望成本公式、前k步累积期望成本公式和可达期望成本公式。

GPoCTL路径公式

$ \varphi::=O \varPhi\left|\varPhi_{1} \cup \varPhi_{2}\right| \diamond \varPhi \mid \square \varPhi, $

其中：Φ、Φ₁、Φ₂是状态公式；O、∪、◇、□分别表示“下一个”、“直到”、“最终”、“总是”。

定义13(GPoCTL语义)

设M_c=(S, Act, p, I, AP, L, C)是一个有穷的CGPDP，||Φ||: S→[0, 1]是S的模糊子集，对于带成本的GPoCTL，其状态公式Φ的语义定义为

$ \| { true } \|(s)=1, $

$ \|a\|(s)=L(s, a), $

$ \left\|\varPhi_{1} \wedge \varPhi_{2}\right\|(s)=\left\|\varPhi_{1}\right\|(s) \wedge\left\|\varPhi_{2}\right\|(s), $

$ \|\neg \varPhi\|(s)=1-\|\varPhi\|(s), $

$ \|G P o(\varphi)\|(s)=G P o(s \mid=\varphi), $

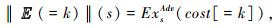
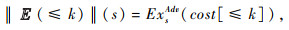
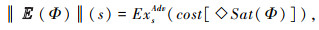
其中：Sat(Φ)={s∈S| ||Φ||(s)>0}。

对于路径公式φ，对应于M_c上语义为||φ||: Paths_Adv(M_c)→[0, 1]，归纳定义为

$ \begin{aligned} &\|\mathrm{O} \varPhi\|(\pi)=p_{A d v}\left(\pi[0], \alpha_{0}, \pi[1]\right) \wedge \\ &\|\varPhi\|(\pi[1]), \end{aligned} $

$ \begin{aligned} &\left\|\varPhi_{1} \cup \varPhi_{2}\right\|(\pi)=\left\|\varPhi_{2}\right\|(\pi[0]) \vee \\ &\bigvee_{j>0}\left(\left\|\varPhi_{1}\right\|(\pi[0]) \wedge\right. \\ &\bigwedge_{k<j} p_{A d v}\left(\pi[k-1], \alpha_{k-1}, \pi[k]\right) \wedge\left\|\varPhi_{1}\right\|(\pi[k]) \wedge \\ &\left.p_{A d v}\left(\pi[j-1], \alpha_{j-1}, \pi[j]\right) \wedge\left\|\varPhi_{2}\right\|(\pi[j])\right), \end{aligned} $

$ \begin{aligned} &\|\diamond \varPhi\|(\pi)=\bigvee_{i=0}^{\infty} \bigwedge_{j=0}^{i-1} p_{A d v}\left(\pi[j], \alpha_{j}, \pi[j+1]\right) \wedge \\ &\|\varPhi\|(\pi[i]), \end{aligned} $

$ \begin{aligned} &\|\square \varPhi\|(\pi)=\bigwedge_{i=0}^{\infty} \bigwedge_{j=0}^{i-1} p_{A d v}\left(\pi[j], \alpha_{j}, \pi[j+1]\right) \wedge \\ &\|\varPhi\|(\pi[i]) 。\end{aligned} $

5 带成本GPoCTL模型检测算法

带成本的GPoCTL模型检测问题描述为：给定CGPDP M_c、M_c中的状态s及GPoCTL状态公式Φ，计算||Φ||(s)的值。对于状态公式Φ=true, Φ=a, Φ=Φ₁∧Φ₂, Φ=┐Φ，可直接由语义给出相应的模型检测算法。对于GPo(φ)算子，引入文献[15]中的算法，包括算法1和算法2。对于第k步瞬时期望成本公式(=k)，前k步累积期望成本公式(≤k)，可达期望成本公式(Φ)，将分别给出它们对应的模型检测算法。

算法1  不动点算法

Require: 不动点函数f

Ensure: 不动点x

procedure FixPoint(x, f)

        x′=f(x)

        while x≠x′ do

        x=x′

x′=f(x)

        end while

        return x

end procedure

算法2主要采用模糊矩阵合成运算方式来计算路径公式的广义可能性。

算法2  计算GPo(φ)的算法

Require: 路径公式φ和CGPDP M_c

Ensure: GPo(φ)的值

procedure GPoCTl(φ)

        case φ

        OΦ return P_Adv°D_Φ°R_Adv

    Φ₁∪Φ₂ return (D_Φ1°P_Adv)^*D_Φ2°R_Adv

    ◇Φ return P_Adv^*°D_Φ2°R_Adv

    □Φ return FixPoint((1)_s∈S, f_Φ)

    end case

end procedure

定义6给出了瞬时期望成本的迭代计算形式，依此可得到瞬时期望成本算子(=k)的递归求解算法，具体步骤详见算法3。

算法3  计算(=k)的算法

Require: CGPDP M_c和步数k

Ensure: M_c中任意状态s，(=k)的值

procedure ExKstep(s, k)

    if k=0 then

      return 0

    end if

    if k=1 then

        return ($\bigvee\limits_{t \in S}$p_Adv(s, α, t))·C_Adv(s, α)

    end if

    return ($\bigvee\limits_{t \in S}$p_Adv(s, α, t))·ExKstep(t, k-1)

end procedure

下面我们给出公式(≤k)满足迭代计算形式的证明。

定理2  给定M_c=(S, Act, p, I, AP, L, C)是一个有穷的CGPDP，对任意s∈S，有

$ \begin{aligned} &E x_{s}^{A d v}({cost}[\leqslant k])=\left(\bigvee_{t \in S} p_{A d v}(s, \alpha, t)\right) \cdot\\ &\left(C_{A d v}(s, \alpha)+E x_{t}^{A d v}({cost}[\leqslant k-1])\right)。\end{aligned} $

证明

$ \begin{aligned} &{Ex}_{s}^{A d v}({cost}[\leqslant k])=\sum\limits_{i=1}^{k} E x_{s}^{A d v}(cost[=i])= \\ &\left(\bigvee_{t \in S} p_{A d v}(s, \alpha, t)\right) \cdot C_{A d v}(s, \alpha)+ \\ &\sum\limits_{i=2}^{k}\left(\bigvee_{t \in S} p_{A d v}(s, \alpha, t)\right) \cdot E x_{t}^{A d v}(cost [=i-1])= \\ &\left(\bigvee_{t \in S} p_{A d v}(s, \alpha, t)\right) \cdot\left(C_{A d v}(s, \alpha)+\right.\\ &\left.\sum\limits_{i=2}^{k} E x_{t}^{A d v}({cost}[=i-1])\right)=\left(\bigvee_{t \in S} p_{A d v}(s, \alpha, t)\right) \cdot\\ &\left(C_{A d v}(s, \alpha)+\sum\limits_{i=1}^{k-1} E x_{t}^{A d v}(cos t[=i])\right)= \\ &\left(\bigvee_{t \in S} p_{A d v}(s, \alpha, t)\right) \cdot\left(C_{A d v}(s, \alpha)+\right. \\ &\left.{Ex}_{t}^{A d v}({cost}[\leqslant k-1])\right)。\end{aligned} $

依据定理2，算法4给出累积期望成本算法。

算法4  计算(≤k)的算法

Require: CGPDP M_c和步数k

Ensure: M_c中任意状态s，(≤k)的值

procedure ExKsteps(s, k)

        if k=0 then

          return 0

        end if

        return ($\bigvee\limits_{t \in S}$p_Adv(s, α, t))·(C_Adv(s, α)+ExKsteps(t, k-1))

end procedure

接下来，我们证明(Φ)满足迭代计算形式。

定理3  给定有穷的CGPDP M_c，对任意s∈S，若GPo(s|=◇Sat(Φ))>0且s∉Sat(Φ)，则有：

$ \begin{aligned} &E x_{s}^{A d v}({cost}[\diamond S a t(\varPhi)])= \\ &\left(\bigvee_{u \in S a t(\varPhi)} p_{A d v}(s, \alpha, u)\right) \cdot C_{A d v}(s, \alpha)+ \\ &\left(\bigvee_{t \in S^{\prime}} p_{A d v}(s, \alpha, t)\right) \cdot E x_{t}^{A d v}({cost}[\diamond {Sat}(\varPhi)])。\end{aligned} $

证明

$ \begin{aligned} &{Ex}_{s}^{A d v}({cost}[\diamond {Sat}(\varPhi)])= \\ &{Ex}_{s}^{A d v}({cost}[\leqslant n(\diamond S a t(\varPhi))])= \\ &\sum\limits_{k=1}^{n} E x_{s}^{A d v}({cost}[=k(\diamond {Sat}(\varPhi))])= \\ &\left(\bigvee_{u \in S a t(\varPhi)} p_{A d v}(s, \alpha, u)\right) \cdot C_{A d v}(s, \alpha)+ \\ &\sum\limits_{k=2}^{n}\left(\bigvee_{t \in S^{\prime}} p_{A d v}(s, \alpha, t)\right) \cdot\\ &E x_{t}^{A d v}({cost}[=k-1(\diamond {Sat}(\varPhi))])= \\ &\left(\bigvee_{u \in S a t(\varPhi)} p_{A d v}(s, \alpha, u)\right) \cdot C_{A d v}(s, \alpha)+\left(\bigvee_{t \in S^{\prime}} p_{A d v}(s, \alpha, t)\right) \cdot \\ &\sum\limits_{i=1}^{n-1} E x_{t}^{A d v}({cost}[=k(\diamond {Sat}(\varPhi))])= \\ &\left(\bigvee_{u \in {Sat}(\varPhi)} p_{A d v}(s, \alpha, u)\right) \cdot C_{A d v}(s, \alpha)+ \\ &\left(\bigvee_{t \in S^{\prime}} p_{A d v}(s, \alpha, t)\right) \cdot\\ &E x_{t}^{A d v}({cost}[\leqslant n-1(\diamond S a t(\varPhi))])= \\ &\left(\bigvee_{u \in S a t(\varPhi)} p_{A d v}(s, \alpha, u)\right) \cdot C_{A d v}(s, \alpha)+ \\ &\left(\bigvee_{t \in S^{\prime}} p_{A d v}(s, \alpha, t)\right) \cdot E x_{t}^{A d v}({cost}[\diamond {Sat}(\varPhi)]) 。\end{aligned} $

其中：S′={s∉Sat(Φ)|GPo(s|=◇Sat(Φ))>0}。

依据定理3，算法5给出可达期望成本算法。

算法5  计算(Φ)的算法

Require: CPDP M_c和状态公式Φ

Ensure: M_c中任意状态s，(Φ)的值

procedure ExPhi(s)

        return ($\bigvee\limits_{u \in {Sat}({\mathit{\Phi}})}$p_Adv(s, α, u))·C_Adv(s, α)+($\bigvee\limits_{t \in S'}$p_Adv(s, α, t))·ExPhi(t)

end procedure

依据算法1~5，算法6给出了带成本的GPoCTL模型检测算法。

算法6  带成本的GPoCTL模型检测算法

Require: CGPDP M_c和状态公式Φ

Ensure: M_c中任意状态s，||Φ||(s)的值

procedure GPoCTLCheck(Φ)

        case Φ

        true return (1)_s∈S

        a∈AP return (||a||(s))_s∈S

        Φ₁∧Φ₂ return (||Φ₁||(s)∧||Φ₂||(s))_s∈S

        ┐Φ return (1-||Φ||(s))_s∈S

        GPo(φ)return GPoCal(φ)

        (=k) return (ExKstep(s, k))_s∈S

        (≤k) return (ExKsteps(s, k))_s∈S

        (Φ) return (ExPhi(s))_s∈S

    end case

end procedure

上述算法的时间复杂度与文献[15]中的计算方法相同，下面进行算法的时间复杂度分析。

在所有调度Adv下，可以在|Φ|步递归计算出||Φ||(s)的值，这里|Φ|表示公式Φ的子公式数，其递归定义如下。

若Φ=a或Φ=true，则|Φ|=1。

$ \left|\varPhi_{1} \wedge \varPhi_{2}\right|=\left|\varPhi_{1}\right|+\left|\varPhi_{2}\right|+1, $

$ |\neg \varPhi|=|\varPhi|+1,|G {Po}(\mathrm{O} \varPhi)|=|\varPhi|+1, $

$ |{GPo}(\diamond \varPhi)|=|\varPhi|+1,|{GPo}(\square \varPhi)|=|\varPhi|+1, $

$ \left|\operatorname{GPo}\left(\varPhi_{1} \cup \varPhi_{2}\right)\right|=\left|\varPhi_{1}\right|+\left|\varPhi_{2}\right|+1, $

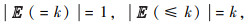
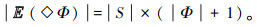
在GPoCTL模型检测算法中，公式Φ=a|Φ₁∧Φ₂|┐Φ|GPo(OΦ)计算||Φ||(s)的时间只与CPDP M_c的大小和公式Φ的长度有关，公式Φ=(=k)(≤k)计算||Φ||(s)的时间只与CPDP M_c的大小、公式Φ的长度和k的大小有关。而计算公式Φ=GPo(Φ₁∪Φ₂)|GPo(◇Φ)的时间主要取决于计算P_Adv的转移闭包P_Adv^*的时间。采用文献[24]的算法来计算P_Adv^*，其时间复杂度为O(n²logn)，其中n=|S|。公式Φ=GPo(□Φ)|(◇Φ)的时间主要取决于迭代时间和矩阵合成运算时间，参照文献[15]的迭代分析，可知迭代计算时间是O(|S|³)。综上所述，通过定理4给定GPoCTL模型检测算法的时间复杂度。

定理4(带成本的GPoCTL模型检测算法的时间复杂度) 给定有穷的CGPDP M_c和带成本的GPoCTL公式Φ、步数k、M_c|=Φ的时间复杂度为O(size(M_f)·poly(S)·|Φ|·k)，其中：size(M_f)是模型的大小；poly(S)是n的多项式函数；|Φ|是公式的长度；k是步数。

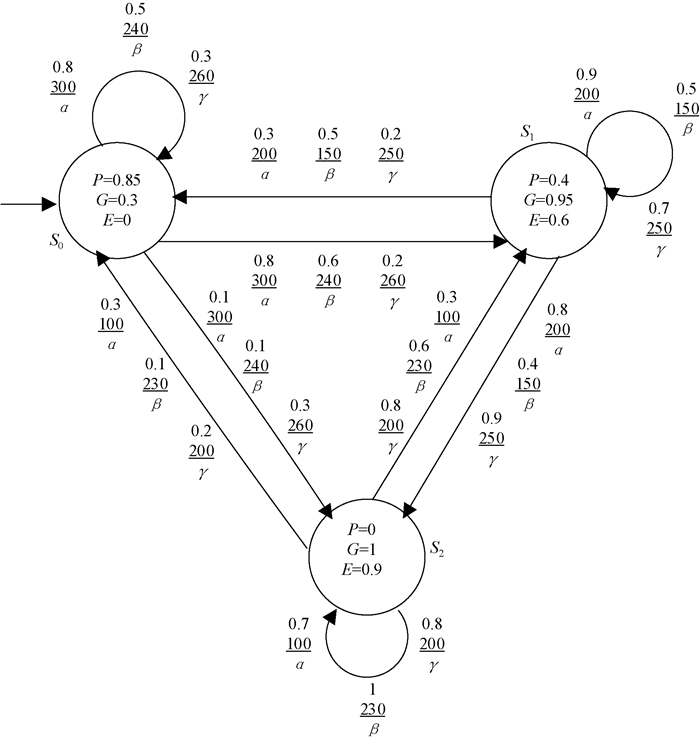
6 实例应用

本文在文献[15]患者诊疗的专家系统的基础上增加了成本回馈，用以说明带成本GPoCTL模型检测算法的实际应用。通过CGPDP M_c=(S, Act, p, I, AP, L, C)来对整个诊疗过程进行建模。s₀、s₁、s₂表示患者的健康状态，原子命题集合AP={P, G, E}表示患者的健康状况为P(差)、G(一般)、E(好)。专家对于患者健康状况的判断是主观的，因此通过给三者赋予模糊值，表示患者的健康程度。三位专家的专业背景与经验存在差异，他们针对患者状况采取的诊疗方案也不尽相同，分别用动作α、β、γ表示。当状态s_i激活某个动作α_i时，会产生成本回馈C(s_i, α_i)，表示该方案的治疗费用。M_c可通过图 2描述。初始分布I及α、β、γ的可能性转移矩阵为

$ \boldsymbol{P}_{I}=\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right), \boldsymbol{P}_{\alpha}=\left(\begin{array}{lll} 0.8 & 0.8 & 0.1 \\ 0.3 & 0.9 & 0.8 \\ 0.3 & 0.7 & 0.3 \end{array}\right), $

$ \boldsymbol{P}_{\beta}=\left(\begin{array}{ccc} 0.5 & 0.6 & 0.1 \\ 0.5 & 0.5 & 0.4 \\ 0.1 & 0.8 & 1 \end{array}\right), \boldsymbol{P}_{\gamma}=\left(\begin{array}{lll} 0.3 & 0.2 & 0.3 \\ 0.2 & 0.7 & 0.9 \\ 0.2 & 0.8 & 0.8 \end{array}\right) 。$

根据算法6，调度Adv取最大值，其过程是优先考虑治愈病人的最大可能性，在此基础上计算期望成本。同理，Adv取最小值则是考虑在治愈的最小可能性基础上计算期望成本。

1) Adv取最大值，调用ExKstep(s₂, 6)迭代计算6次，最终计算得到从s₂出发第6步的最大可能性瞬时期望成本||(=6)||_max(s₂)=230。再令Adv取最小值，调用ExKstep(s₂, 6)迭代计算6次，最终计算得到最小可能性瞬时期望成本||(=6)||_min(s₂)=11.76。说明在状态Adv，医生采用3种治疗方案治疗6次后，第6次治疗的最大可能性期望费用为230，最小可能性期望费用为11.76。

2) Adv取最大值，调用ExKsteps(s₀, 6)迭代计算6次，最终得到从s₀出发前6步的最大可能性累积期望成本||(≤6)||_max(s₀)=1 082.4。再令Adv取最小值，调用ExKsteps(s₀, 6)迭代计算6次，最终计算得到从s₀出发前6步的最小可能性累积期望成本||(≤6)||_min(s₀)=111.3。说明在状态||E||(s₀)=0，医生采用3种治疗方案治疗6次后，6次治疗的累积最大可能性期望费用为1 082.4，最小可能性期望费用为111.3。

3) 由||E||(s₀)=0，||E||(s₁)=0.6，||E||(s₂)=0.9，得Sat(E)={s₁, s₂}。Adv取最大值，迭代调用ExPhi(s₀)，得到从s₀出发，最终到达Sat(E)的最大可能性可达期望成本||(E)||_max(s₀)=432。再令Adv取最小值，迭代调用ExPhi(s₀)，计算得到从状态s₀出发，最终到达Sat(E)的最小可能性可达期望成本||(E)||_min(s₀)=101.4。说明在状态s₀，医生采用3种治疗方案治疗多次后，病人最终健康状况为“好”的最大可能性期望费用为432，最小可能性期望费用为101.4。

7 结束语

为解决GPoCTL模型检测中的成本问题，本文提出了带成本的GPoCTL模型检测方法。引入了带成本的广义可能性决策过程模型并在此基础上给出了期望成本，进而扩展得到带成本GPoCTL，增强了原有逻辑的表达能力。接着通过证明期望算子满足迭代计算形式，从而扩展了带成本的GPoCTL模型检测算法，最后通过实例说明其实际应用。