三支概念分析(three-way concept analysis,3WCA)[1]理论是结合形式概念分析[2]和三支决策理论[3]提出的,它是一种新的知识表示与知识发现的理论方法.目前已有一些基于三支概念分析理论的研究成果.文献[4]研究了TWCA以及三支概念格和经典概念格之间的联系;文献[5]研究了基于三支概念分析的属性约简问题;文献[6-7]针对决策形式背景的规则提取方法进行了研究;文献[8-9]分别提出了三支概念的构建算法CbO3C和PCbO3C,其中CbO3C借鉴CbO算法[10]的思想,PCbO3C是利用多线程技术并行计算核心三支概念.
蕴含规则的挖掘算法不断得到优化[11],在形式概念分析中获取蕴含规则是一项重要的研究内容.文献[12]提出构建概念格线图的增量式算法CLearner,并在此基础上获取关联规则,文献[13]基于属性约简和近似属性约简的概念提出属性蕴含和关联规则的获取方法.以上主要研究属性子集之间的“具有”关系,即正属性蕴含.忽视形式背景中负属性蕴含的信息可能会得到不完整的结论,比如仅考虑正属性无法表示蕴含规则:“鸵鸟是鸟,但不会飞”.在形式概念分析理论的基础上属性子集之间的“不具有”关系也已经被研究.文献[14]结合NextClosure算法提出混合属性蕴含的获取方法,文献[15-16]基于原形式背景与其补形式背景的并置提出混合属性蕴含的获取方法.三支概念分析中三支算子可以同时表示数据集中“共同具有”和“共同不具有”这两种语义,当针对属性集进行考虑时,“共同具有”和“共同不具有”的属性子集分别对应正属性蕴含和负属性蕴含的前件或后件,利用三支算子可直接基于原形式背景获取混合属性蕴含,在一定程度上减少了计算量和存储空间.因此,本文基于三支概念分析理论研究混合蕴含规则,结合三支概念的构建算法给出三支概念格线图的构建方法,最后,基于三支概念格线图给出混合蕴含规则成立的条件.
1 基础知识本节给出所需要用到的三支概念分析理论的相关定义.
定义1[17] 形式背景(U, V, R)包括两个集合U和V,以及二者之间的关系R.U中的每个元素称为对象,V中的每个元素称为属性.对象u与属性v有关系R,记为uRv,读作“对象u具有属性v”.
定义2[17] 设(U, V, R)是一个形式背景,对于任意的对象子集X⊆U和属性子集A⊆V, 一对算子*:P(U)→P(V)和*:P(V)→P(U)定义为X*={v∈V|∀u∈X(uRv)},A*={u∈U|∀v∈A(uRv)},其中P(·)表示幂集.
如果X*=A与A*=X同时成立,则称(X, A)为(U, V, R)的一个形式概念(简称概念),X称为概念(X, A)的外延,A称为内涵.特别地,对于对象u∈U,相应的对象概念[18]为:γu=({u}**, {u}*).对于属性v∈V,相应的属性概念[18]为:μv=({v}*, {v}**).
形式背景(U, V, R)中所有的形式概念组成了一个完备格,称为(U, V, R)的概念格,并记为CL(U, V, R).
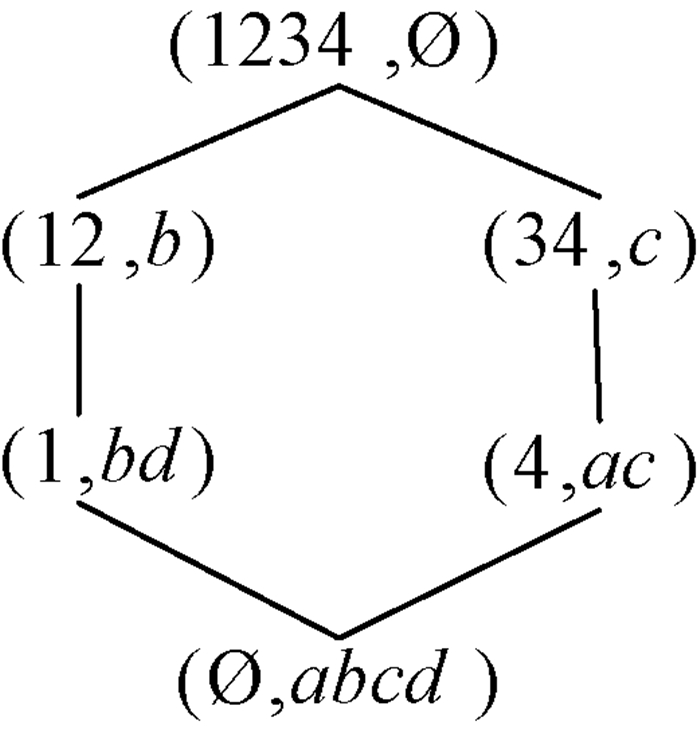
例1 表 1是形式背景(U, V, R),其中U={1, 2, 3, 4},V={a, b, c, d}.图 1为(U, V, R)对应的概念格CL(U, V, R).并且(U, V, R)中所有的对象概念为
| $ \begin{align} & \gamma \left( 1 \right)=\left( \left\{ 1 \right\},\{b,d\} \right),\gamma \left( 2 \right)=\left( \left\{ 1,2 \right\},\{b\} \right), \\ & \gamma \left( 3 \right)=\left( \left\{ 3,4 \right\},\{c\} \right),\gamma \left( 4 \right)=\left( \left\{ 4 \right\},\{a,c\} \right). \\ \end{align} $ |
|
|
表 1 形式背景(U,V,R) Table 1 A formal context (U,V,R) |
|
图 1 CL(U,V,R) Figure 1 CL(U,V,R) |
所有的属性概念为
| $ \begin{align} & \mu \left( a \right)=\left( \left\{ 4 \right\},\{a,c\} \right),\mu \left( b \right)=\left( \left\{ 1,2 \right\},\{b\} \right), \\ & \mu \left( c \right)=\left( \left\{ 3,4 \right\},\{c\} \right),\mu \left( d \right)=\left( \left\{ 1 \right\},\{b,d\} \right). \\ \end{align} $ |
在三支概念分析中文献[1]将定义2给出的算子称为正算子,并给出相应负算子的定义.
定义3[1] 设(U, V, R)是一个形式背景,对于任意的对象子集X⊆U和属性子集A⊆V, 一对算子
| $ {{X}^{{\bar{*}}}}=\left\{ v\in V\text{ }\!\!|\!\!\text{ }\forall u\in X\left( \neg \left( uRv \right) \right) \right\},{{A}^{{\bar{*}}}}=\left\{ u\in U\text{ }\!\!|\!\!\text{ }\forall v\in A\left( \neg \left( uRv \right) \right) \right\}. $ |
文献[1]把正算子和负算子结合起来形成两对三支算子,分别称为OE算子和AE算子.
定义4[1] 设(U, V, R)是一个形式背景,对于任意的对象子集X, Y⊆U和属性子集A, B⊆V,一对OE算子<·: P(U)→DP(V)和·>: DP(V)→P(U)定义为X<·=(X*, X
如果X<·=(A, B)与(A, B)·>=X同时成立,则称(X, (A, B))为(U, V, R)的一个对象导出三支概念,简称OE概念.X称为(X, (A, B))的外延,(A, B)称为(X, (A, B))的内涵,由所有OE概念组成的集合记作OEL(U, V, R),叫作对象导出三支概念格,简称OE概念格.
如果(X,Y)·>=A与A<·=(X,Y)同时成立,则称((X, Y), A)为(U, V, R)的一个属性导出三支概念,简称AE概念.(X, Y)称为((X, Y), A)的外延,A称为((X, Y), A)的内涵.由所有AE概念组成的集合记作AEL(U, V, R),叫作属性导出三支概念格,简称AE概念格.
∀u∈U,v∈V,根据OE概念的性质,容易确定({u}**∩{u}
对于对象子集X⊆U,属性子集A⊆V,有
| $ \begin{align} &{{\gamma }_{OE}}\left( X \right)=\left\{ {{\gamma }_{OE}}\left( u \right)|\forall u\in X \right\}, {{\beta }_{OE}}\left( A \right)=\left\{ {{\beta }_{OE}}\left( v \right)|\forall v\in A \right\}, {{{\bar{\beta }}}_{OE}}\left( A \right)=\left\{ {{{\bar{\beta }}}_{OE}}\left( v \right)|\forall v\in A \right\}; \\ &{{\beta }_{AE}}\left( A \right)=\{{{\beta }_{AE}}\left( v \right)|\forall v\in A\}, {{\gamma }_{AE}}\left( X \right)=\{{{\gamma }_{AE}}\left( u \right)|\forall u\in X\}, {{{\bar{\gamma }}}_{AE}}\left( X \right)=\{{{{\bar{\gamma }}}_{AE}}\left( u \right)|\forall u\in X\}. \\ \end{align} $ |
对于OE概念(X, (A, B))和(Y, (C, D)),若满足偏序关系:(X, (A, B))≤(Y, (C, D))
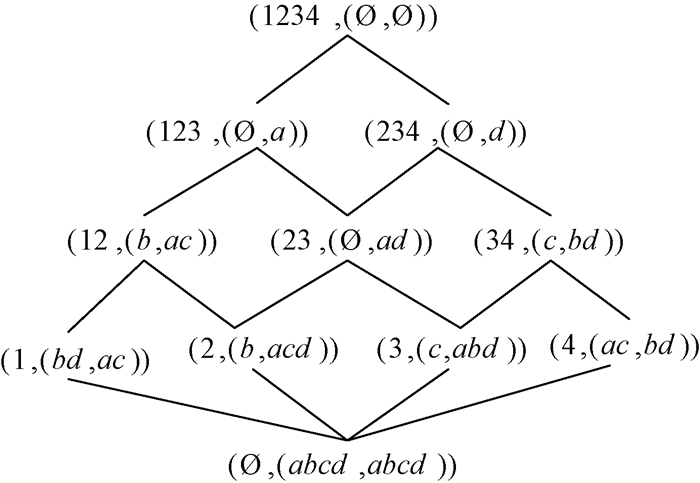
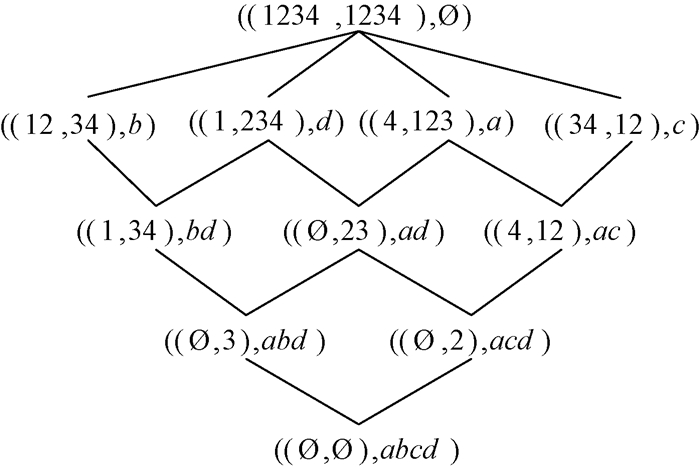
例2 形式背景(U, V, R)(表 1)对应的OEL(U, V, R)和AEL(U, V, R)分别如图 2和图 3所示.
|
图 2 OEL(U,V,R) Figure 2 OEL(U,V,R) |
|
图 3 AEL(U,V,R) Figure 3 AEL(U,V,R) |
下面给出属性蕴含定义以及相关性质.
定义5[18] 设(U, V, R)为形式背景,A, B⊆V,若满足“具有A中所有属性的对象也具有B中所有属性”,则称属性蕴含A→B在(U, V, R)中成立.属性蕴含A→B在(U, V, R)中成立,当且仅当A*⊆B*.
形式背景(U, V, R)中对象之间的蕴含规则也可被类似地讨论.
设(U, V, R)为形式背景,X, Y⊆U,如果满足“对象集X共同具有的属性,对象集Y也共同具有”,则称对象蕴含X→Y在(U, V, R)中成立.对象蕴含X→Y在(U, V, R)中成立,当且仅当X*⊆Y*.
2 三支概念格线图概念格线图以一种简洁的形式表示对象集和属性集之间的“具有”关系,为了能以同样的形式表示对象集和属性集之间“具有”和“不具有”的关系,本节针对三支概念格线图进行研究.
2.1 对象导出三支概念格线图对象导出三支概念格线图可基于对象导出三支概念格获得,具体步骤如下:
(1) 根据三支概念的构建算法[8-9]构建OEL(U, V, R),并用小圆圈代表每一个OE概念;
(2) 计算所有的对象OE概念γOE(U),正属性OE概念βOE(V)和负属性OE概念
(3) ∀u∈U,用“u”标记对象OE概念({u}**∩{u}
(4) ∀v∈V,用“v+”标记正属性OE概念({v}*, ({v}**, {v}
构建属性导出三支概念格线图的具体步骤如下:
(1) 根据三支概念的构建算法[8-9]构建AEL(U, V, R),并用小圆圈代表每一个AE概念;
(2) 计算属性AE概念βAE(V),正对象AE概念γAE(U)和负对象AE概念
(3) ∀v∈V,用“v”标记属性AE概念(({v}*, {v}
(4) ∀u∈U,用“u+”标记正对象AE概念(({u}**, {u}
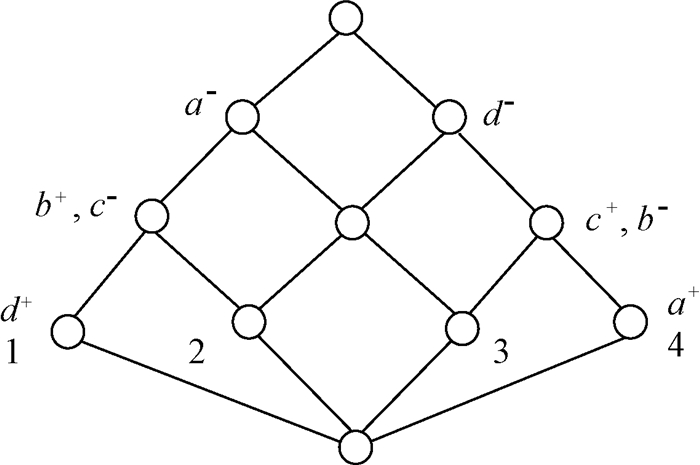
例3 对于形式背景(U, V, R)(表 1),对象导出三支概念格线图和属性导出三支概念格线图分别如图 4和图 5所示.此处仅以对象导出三支概念格线图为例,给出如下具体构建过程:
|
图 4 三支概念格线图OEL(U,V,R) Figure 4 The line diagram of OEL(U,V,R) |
|
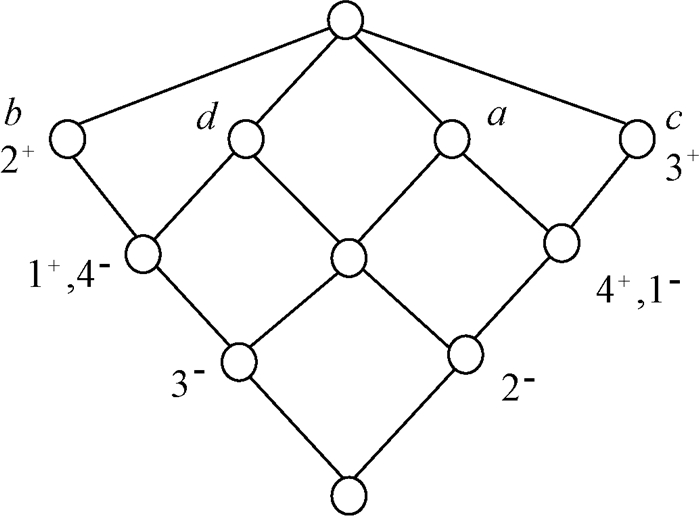
图 5 三支概念格线图AEL(U,V,R) Figure 5 The line diagram of AEL(U,V,R) |
(1) 构建OEL(U, V, R).不同于图 2,这里仅用小圆圈代表每一个OE概念;
(2) 计算所有的对象OE概念:γOE(1)=({1}, ({b, d}, {a, c})),γOE(2)=({2}, ({b}, {a, c, d})),γOE(3)=({3}, ({c}, {a, b, d})),γOE(4)=({4}, ({a, c}, {b, d}));正属性OE概念:βOE(a)=({4}, ({a, c}, {b, d})),βOE(b)=({1, 2}, ({b}, {a, c})),βOE(c)=({3, 4}, ({c}, {b, d})),βOE(d)=({1}, ({b, d}, {a, c}));负属性OE概念:
(3) 标记对象OE概念.比如,用“1”标记对象1的对象OE概念({1}, ({b, d}, {a, c}));
(4) 标记正属性OE概念和负属性OE概念.比如,用“a+”标记a的正属性OE概念({4}, ({a, c}, {b, d})),用“a-”标记a的负属性OE概念({1, 2, 3}, (
首先基于三支概念分析理论提出混合属性蕴含的定义,然后讨论如何基于对象导出三支概念格线图获取混合属性蕴含,利用类似的方法对混合对象蕴含展开研究.混合属性蕴含的获取是基于对象导出三支概念格线图,而混合对象蕴含的获取是基于属性导出三支概念格线图.
3.1 混合属性蕴含三支概念分析下混合属性蕴含的定义如下.
定义6 设(U, V, R)是一个形式背景,A, B, C, D⊆V,如果满足“拥有A中所有属性并且不拥有B中任意属性的对象拥有C中所有属性且不拥有D中任意属性”,则称混合属性蕴含(A, B)→(C, D)在(U, V, R)中成立.其中二元组(A, B)称为(A, B)→(C, D)的前件,二元组(C, D)称为后件.
根据混合属性蕴含的定义和OE算子的性质,可得以下结论.
定理1 设(U, V, R)是一个形式背景,A, B, C, D⊆V,混合属性蕴含(A, B)→(C, D)在(U, V, R)中成立的充分必要条件为:(A, B)·>⊆(C, D)·>.
例4 混合属性蕴含({d},
| $ \left\{ 1 \right\}={{\left\{ d \right\}}^{*}}\cap {{\varnothing }^{{\bar{*}}}}=\left( \left\{ d \right\}, \varnothing \right)\subseteq \left( \left\{ b \right\}, \{c\} \right)={{\left\{ b \right\}}^{*}}\cap {{\left\{ c \right\}}^{{\bar{*}}}}=\left\{ 1, 2 \right\}, $ |
然而,混合属性蕴含({c},
| $ \left\{ 3, 4 \right\}={{\left\{ c \right\}}^{*}}\cap {{\varnothing }^{{\bar{*}}}}=\left( \left\{ c \right\}, \varnothing \right)\nsubseteq \left( \left\{ a \right\}, \{b\} \right)={{\left\{ a \right\}}^{*}}\cap {{\left\{ b \right\}}^{{\bar{*}}}}=\left\{ 4 \right\}. $ |
根据混合属性蕴含的定义和对象导出三支概念格线图的性质,可得以下定理.
定理2 设(U, V, R)是一个形式背景,A, B, C, D⊆V,混合属性蕴含(A, B)→(C, D)在(U, V, R)中成立,当且仅当∧(βOE(A)∪
证明 由OE概念之间偏序关系的性质以及OE概念之间下确界的定义可知,
| $ \begin{align} &\wedge ({{\beta }_{OE}}\left( A \right)\cup {{{\bar{\beta }}}_{OE}}\left( B \right))\le \wedge ({{\beta }_{OE}}\left( C \right)\cup {{{\bar{\beta }}}_{OE}}\left( D \right))\Leftrightarrow \underset{a\in A}{\mathop{\cap }}\, {{a}^{*}}\cap \underset{b\in B}{\mathop{\cap }}\, {{b}^{{\bar{*}}}}\subseteq \underset{c\in C}{\mathop{\cap }}\, {{c}^{*}}\cap \underset{d\in D}{\mathop{\cap }}\, {{d}^{{\bar{*}}}}\Leftrightarrow \\ &{{\left( A, B \right)}^{\cdot >}}\subseteq {{\left( C, D \right)}^{\cdot >}}. \\ \end{align} $ |
又由定理1可知定理2成立.
由定理2可知,根据对象导出三支概念格线图可以判断任意给定的混合属性蕴含是否成立.
例5 混合属性蕴含({a, c},
当具有相同属性的对象被要求划分为同一类时,对象蕴含可以给出表示.然而,如果同时需要考虑不拥有某些属性的对象,混合对象蕴含将是更好的表达方式.接下来在三支概念分析理论的基础上针对混合对象蕴含进行研究,混合对象蕴含的定义如下.
定义7 设(U, V, R)是一个形式背景,X, Y, Z, W⊆U,如果满足“被X中所有对象拥有并且不被Y中任意对象所拥有的属性,被Z中所有对象拥有且不被W中任意对象所拥有”,则称混合对象蕴含(X, Y)→(Z, W)在(U, V, R)中成立.其中二元组(X, Y)称为(X, Y)→(Z, W)的前件,二元组(Z, W)称为后件.
根据混合对象蕴含和AE算子的定义,可得以下定理.
定理3 设(U, V, R)是一个形式背景,X, Y, Z, W⊆U,混合对象蕴含(X, Y)→(Z, W)在(U, V, R)中成立,当且仅当(X, Y)·>⊆(Z, W)·>.
根据混合对象蕴含的定义和属性导出三支概念格线图的性质,可得以下定理.
定理4 设(U, V, R)是一个形式背景,X, Y, Z, W⊆U,混合对象蕴含(X, Y)→(Z, W)在(U, V, R)中成立,如果∨(γAE(Z)∪
证明 证明方法同定理2.
由定理4可知,根据属性导出三支概念格线图可以判断任意给定的混合对象蕴含是否成立.
4 结论基于三支概念分析理论对混合蕴含规则进行研究,首先提出混合属性蕴含和混合对象蕴含的定义,结合三支算子的性质给出其成立的充分必要条件,然后提出三支概念格线图的构建方法并在此基础上获取混合蕴含规则.三支概念格线图为数据可视化提供了工具,其相对概念格提供了更多的信息,而混合属性蕴含可用于数据挖掘、机器学习等领域,比如利用正、负关联规则用于分类[19]以及文本聚类[20]等.混合蕴含规则的获取以及生成混合蕴含规则的基是至关重要的,未来将针对此问题进行深入的研究.
| [1] |
QI J J, WEI L, YAO Y Y. Three-way formal concept analysis [C]//Proceedings of International Conference on Rough Sets and Knowledge Technology. Shanghai, 2014:732-741.
(  0) 0) |
| [2] |
WILLE R.Restructuring lattices theory: an approach based on hierarchies of concepts [C]//Proceedings of the 7th International Conference on Formal Concept Analysis. Darmstadt, 2009:314-339.
(  0) 0) |
| [3] |
YAO Y Y. An outline of a theory of three-way decisions [C]// Proceedings of the 8th International Conference on Rough Sets and Current Trends in Computing. Chengdu, 2012: 1-17.
(  0) 0) |
| [4] |
QI J J, QIAN T, WEI L. The connections between three-way and classical concept lattices[J]. Knowledge-based systems, 2016, 91: 143-151. DOI:10.1016/j.knosys.2015.08.006 (  0) 0) |
| [5] |
REN R S, WEI L. The attribute reductions of three-way concept lattices[J]. Knowledge-based systems, 2016, 99: 92-102. DOI:10.1016/j.knosys.2016.01.045 (  0) 0) |
| [6] |
刘琳, 钱婷, 魏玲. 基于属性导出三支概念格的决策背景规则提取[J]. 西北大学学报(自然科学版), 2016, 46(4): 481-487. (  0) 0) |
| [7] |
刘琳, 魏玲, 钱婷. 决策形式背景中具有置信度的三支规则提取[J]. 山东大学学报(理学版), 2017, 52(2): 101-110. (  0) 0) |
| [8] |
汪文威, 祁建军. 三支概念的构建算法[J]. 西安电子科技大学学报(自然科学版), 2017, 44(1): 77-82. (  0) 0) |
| [9] |
祁建军, 汪文威. 多线程并行构建三支概念[J]. 西安交通大学学报(自然科学版), 2017, 51(3): 116-121. (  0) 0) |
| [10] |
ANDREWS S. A 'Best-of-Breed'approach for designing a fast algorithm for computing fixpoints of Galois connections[J]. Information sciences, 2015, 295: 633-649. DOI:10.1016/j.ins.2014.10.011 (  0) 0) |
| [11] |
王青, 谭良, 杨显华. 基于Spark的Apriori并行算法优化实现[J]. 郑州大学学报(理学版), 2016, 48(4): 60-64. (  0) 0) |
| [12] |
GALLO A, MEO R. Using a reinforced concept lattice to incrementally mine association rules from closed itemsets[M]// Knowledge Discovery in Inductive Databases. Berlin: Springer, 2007:97-115.
(  0) 0) |
| [13] |
XIE Z, LIU Z. From intent reducts for attribute implications to approximate intent reducts for association rules[C]//Proceedings of the 5th International Conference on Computer and Information Technology. Gazirpur, 2005: 162-169.
(  0) 0) |
| [14] |
RODRÍGUEZ-JIMÉNEZ J M, CORDERO P, ENCISO M, et al. Negative attributes and implications in formal concept analysis[J]. Procedia computer science, 2014, 31: 758-765. DOI:10.1016/j.procs.2014.05.325 (  0) 0) |
| [15] |
MISSAOUI R, NOURINE L, RENAUD Y. An inference system for exhaustive generation of mixed and purely negative implications from purely positive ones[C]//Proceedings of the 7th International Conference on Concept Lattices and Their Applications. Sevilla, 2010:271-282.
(  0) 0) |
| [16] |
MISSAOUI R, NOURINE L, RENAUD Y. Computing implications with negation from a formal context[J]. Fundamenta informaticae, 2012, 115(4): 357-375. (  0) 0) |
| [17] |
GANTER B, WILLE R. Formal concept analysis, mathematical foundations[M]. Berlin: Springer-Verla, 1999.
(  0) 0) |
| [18] |
GANTER B, OBIEDKOV S. Conceptual exploration[M]. Berlin: Springer-Verla, 2016.
(  0) 0) |
| [19] |
ANTONIE M L. An associative classifier based on positive and negative rules[C]//The 9th Workshop on Research Issues in Data Mining and Knowledge Discovery. Paris, 2004:64-69.
(  0) 0) |
| [20] |
曲守宁, 王钦, 邹燕, 等. 基于关联规则的文本聚类算法的研究[J]. 计算机应用研究, 2008, 25(4): 986-988. (  0) 0) |
 2017, Vol. 49
2017, Vol. 49


