2. 江苏省大数据分析技术重点实验室 江苏 南京210044
2. Jiangsu Key Laboratory of Big Data Analysis Technology /B-DAT, Nanjing 210044, China
粗糙集理论[1]是一种处理不确定性问题的有效工具,主要利用知识约简直接从给定的数据集中挖掘出有效的确定性和不确定性决策规则.由于没有考虑到容错性,并且缺乏一定的语义,Yao通过引入贝叶斯风险分析,提出了具有容错能力的决策粗糙集模型,可以生成三支决策[2].该模型在聚类分析、推荐系统、图像处理、认知学习等方面取得了成功应用[3-8].
传统决策粗糙集模型主要基于单个粒度,文献[9]结合多粒度思想提出了乐观和悲观的多粒度决策粗糙集模型,将决策粗糙集模型研究从单粒度推广到多粒度环境,为解决多个粒度的问题提供了一种新的有效方法.一些学者将多粒度决策粗糙集模型中等价关系推广为优势关系、相容关系、模糊关系等,得到了许多新型的多粒度决策粗糙集模型[10-21].传统多粒度决策粗糙集模型中下近似和上近似都采用同一乐观或悲观的策略,如果上下近似采用不同策略,将产生另外两种新模型.为此,本文提出了乐观-悲观和悲观-乐观的多粒度决策粗糙集模型,探讨了这两种模型的正确性和合理性,分析了不同多粒度决策粗糙集模型之间的相互关系,这将为多粒度决策分析提供一个新的视角.
1 决策粗糙集概念下面简要介绍本文主要用到的DTRS模型一些基本概念,详细的介绍请参考有关文献[1-2, 9].
定义1[1] 设决策表S=(U,At=C∪D,{Va|a∈At}, {Ia|a∈At}),其中U={x1,x2,…, xn}表示对象的非空有限集合,称为论域; At为全体属性集,C为条件属性集,D为决策属性集; Va是属性a∈At的值域; Ia:U→Va是一个信息函数.每一个属性子集A⊆At决定了一个二元不可区分关系IND(A):
| $ IND\left( A \right) = \left\{ {\left( {x,y} \right) \in U \times U\left| {\forall a \in A,{I_a}\left( x \right) = {I_a}\left( y \right)} \right.} \right\}. $ |
关系IND(A)构成了U的一个划分,用U/IND(A)表示,简记为U/A或πA.条件属性集C导出的U上划分为πC={C1,C2,…,Cp},决策属性D导出的U上划分记为πD={D1,D2,…,Dk}.
在Pawlak近似空间中,通常用等价类[x]来表示对象x.由于实际应用中经常出现不一致数据,通常将一个对象x尽可能正确地划分到正区域POS(X),边界域BND(X)或负区域NEG(X)中.根据贝叶斯理论和最小风险准则,存在一种特殊情况下损失函数应满足λPP≤λBP < λNP和λNN≤λBN < λPN.于是,可计算出α和β两个阈值(0≤β < α≤1),即
| $ \alpha = \frac{{\left( {{\lambda _{PN}} - {\lambda _{BN}}} \right)}}{{\left( {{\lambda _{PN}} - {\lambda _{BN}}} \right) + \left( {{\lambda _{BP}} - {\lambda _{PP}}} \right)}},\beta = \frac{{\left( {{\lambda _{BN}} - {\lambda _{NN}}} \right)}}{{\left( {{\lambda _{BN}} - {\lambda _{NN}}} \right) + \left( {{\lambda _{NP}} - {\lambda _{BP}}} \right)}}. $ |
定义2[2] 在决策表S中, 对于一个决策类Dj∈πD,相对于πA的(α, β)-概率下近似集与概率上近似集定义如下:
| $ \underline {{A^{\left( {\alpha ,\beta } \right)}}\left( {{D_j}} \right)} = \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_A}} \right.} \right) \ge \alpha } \right.} \right\} = \bigcup\limits_{p\left( {{D_j}\left| {{{\left[ x \right]}_A}} \right.} \right) \ge \alpha } {{{\left[ x \right]}_A}} ; $ |
| $ \overline {{A^{\left( {\alpha ,\beta } \right)}}\left( {{D_j}} \right)} = \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_A}} \right.} \right) > \beta } \right.} \right\} = \bigcup\limits_{p\left( {{D_j}\left| {{{\left[ x \right]}_A}} \right.} \right) > \beta } {{{\left[ x \right]}_A}} . $ |
其中:
根据定义2,利用决策类Dj可将U划分为3个概率区域,分别为:
| $ PO{S^{\left( {\alpha ,\beta } \right)}}\left( {{D_j}\left| {{\pi _A}} \right.} \right) = \underline {{A^{\left( {\alpha ,\beta } \right)}}\left( {{D_j}} \right)} ; $ |
| $ BN{D^{\left( {\alpha ,\beta } \right)}}\left( {{D_j}\left| {{\pi _A}} \right.} \right) = \overline {{A^{\left( {\alpha ,\beta } \right)}}\left( {{D_j}} \right)} - \underline {{A^{\left( {\alpha ,\beta } \right)}}\left( {{D_j}} \right)} ; $ |
| $ NE{G^{\left( {\alpha ,\beta } \right)}}\left( {{D_j}\left| {{\pi _A}} \right.} \right) = U - \overline {{A^{\left( {\alpha ,\beta } \right)}}\left( {{D_j}} \right)} . $ |
因此,决策粗糙集模型中πD的3个概率区域可表示为:
| $ PO{S^{\left( {\alpha ,\beta } \right)}}\left( {{\pi _D}\left| {{\pi _A}} \right.} \right) = \left\{ {x \in U\left| {p\left( {{D_{\max }}\left( {{{\left[ x \right]}_A}} \right)\left| {{{\left[ x \right]}_A}} \right.} \right) \ge \alpha } \right.} \right\}; $ |
| $ BN{D^{\left( {\alpha ,\beta } \right)}}\left( {{\pi _D}\left| {{\pi _A}} \right.} \right) = \left\{ {x \in U\left| {\beta < p\left( {{D_{\max }}\left( {{{\left[ x \right]}_A}} \right)\left| {{{\left[ x \right]}_A}} \right.} \right) < \alpha } \right.} \right\}; $ |
| $ NE{G^{\left( {\alpha ,\beta } \right)}}\left( {{\pi _D}\left| {{\pi _A}} \right.} \right) = \left\{ {x \in U\left| {p\left( {{D_{\max }}\left( {{{\left[ x \right]}_A}} \right)\left| {{{\left[ x \right]}_A}} \right.} \right) \le \beta } \right.} \right\}. $ |
其中:
定义3[9] 在决策表S中,A={A1,A2,…, Am}是At的m个属性子集族,则定义Dj的关于属性子集A1,A2,…, Am的乐观多粒度决策粗糙集模型的下近似和上近似为:
| $ \underline {\sum\limits_{i = 1}^m {A_i^{O,\left( {\alpha ,\beta } \right)}\left( {{D_j}} \right)} } = \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) \ge \alpha } \right. \vee p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right)\\ \ge \alpha \vee \cdots \vee p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) \ge \alpha } \right\}; $ |
| $ \begin{array}{l} \overline {\sum\limits_{i = 1}^m {A_i^{O,\left( {\alpha ,\beta } \right)}\left( {{D_j}} \right)} } = U - \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) \ge \beta } \right. \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right)\\ \ge \beta \wedge \cdots \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) \ge \beta } \right\} = \\ \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) > \beta } \right. \vee p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right) > \beta \vee \cdots \vee p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) > \beta } \right\}. \end{array} $ |
性质1 在决策表S中,A={A1,A2,…, Am}是At的m个属性子集族,乐观多粒度粗糙集模型有下列性质:
| $ 1)\underline{\sum\limits_{i=1}^{m}{{{A}_{i}}^{O, (\alpha, \beta )}({{D}_{j}})}}=\underset{i=1}{\overset{m}{\mathop{\cup }}}\, \underline{{{A}_{i}}^{(\alpha, \beta )}({{D}_{j}})};2)\overline{\sum\limits_{i=1}^{m}{{{A}_{i}}^{O, (\alpha, \beta )}({{D}_{j}})}}=\underset{i=1}{\overset{m}{\mathop{\cup }}}\, \overline{{{A}_{i}}^{(\alpha, \beta )}({{D}_{j}})}. $ |
定义4[9] 在决策表S中,A={A1,A2,…, Am}是At的m个属性子集族,则定义Dj的关于属性子集A1,A2,…, Am的悲观多粒度决策粗糙集模型的下近似和上近似为:
| $ \underline {\sum\limits_{i = 1}^m {A_i^{P,\left( {\alpha ,\beta } \right)}\left( {{D_j}} \right)} } = \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) \ge \alpha } \right. \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right)\\ \ge \alpha \wedge \cdots \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) \ge \alpha } \right\}; $ |
| $ \begin{array}{l} \overline {\sum\limits_{i = 1}^m {A_i^{P,\left( {\alpha ,\beta } \right)}\left( {{D_j}} \right)} } = U - \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) \le \beta } \right. \vee p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right)\\ \le \beta \vee \cdots \vee p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) \le \beta } \right\} = \\ \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) > \beta } \right. \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right) > \beta \wedge \cdots \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) > \beta } \right\}. \end{array} $ |
性质2 在决策表S中,A={A1,A2,…, Am}是At的m个属性子集族,悲观多粒度粗糙集模型有下列性质:
| $ 1)\underline{\sum\limits_{i=1}^{m}{{{A}_{i}}^{P, (\alpha, \beta )}({{D}_{j}})}}=\underline{\underset{i=1}{\overset{m}{\mathop{\cap }}}\, {{A}_{i}}^{(\alpha, \beta )}({{D}_{j}})};2)\overline{\sum\limits_{i=1}^{m}{{{A}_{i}}^{P, (\alpha, \beta )}({{D}_{j}})}}=\overline{\underset{i=1}{\overset{m}{\mathop{\cap }}}\, {{A}_{i}}^{(\alpha, \beta )}({{D}_{j}})}. $ |
为统一表示和区别,定义3、4的乐观和悲观多粒度决策粗糙集模型中下近似和上近似可以分别记为
在传统的乐观和悲观多粒度决策粗糙集模型中,上下近似要么都采用乐观策略,要么都采用悲观策略.在现实情形下,可能还存在两种情况:1)下近似采用乐观策略,上近似采用悲观策略; 2)下近似采用悲观策略,上近似采用乐观策略.下面先给出这两种多粒度决策粗糙集模型的定义,然后探讨这两种模型的正确性和合理性以及不同多粒度决策粗糙集模型之间的关系.
2.1 两种新型的多粒度决策粗糙集模型定义5 在决策表S中,A={A1,A2,…, Am}是At的m个属性子集族,则定义Dj的关于属性子集A1,A2,…, Am的乐观-悲观多粒度决策粗糙集模型的下近似和上近似分别为:
| $ \underline {\sum\limits_{i = 1}^m {A_i^{OP,\left( {\alpha ,\beta } \right)}\left( {{D_j}} \right)} } = \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) \ge \alpha } \right. \vee p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right)\\ \ge \alpha \vee \cdots \vee p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) \ge \alpha } \right\}; $ |
| $ \begin{array}{l} \overline {\sum\limits_{i = 1}^m {A_i^{OP,\left( {\alpha ,\beta } \right)}\left( {{D_j}} \right)} } = U - \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) \le \beta } \right. \vee p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right) \le \beta \vee \cdots \vee p\\\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) \le \beta } \right\} = \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) > \beta } \right. \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right)\\ > \beta \wedge \cdots \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) > \beta } \right\}. \end{array} $ |
性质3 在决策表S中,A={A1,A2,…, Am}是At的m个属性子集族,乐观-悲观多粒度粗糙集模型有下列性质:
| $ 1)\underline{\sum\limits_{i=1}^{m}{{{A}_{i}}^{OP, (\alpha, \beta )}({{D}_{j}})}}=\underset{i=1}{\overset{m}{\mathop{\cup }}}\, \underline{{{A}_{i}}^{(\alpha, \beta )}({{D}_{j}})};2)\overline{\sum\limits_{i=1}^{m}{{{A}_{i}}^{OP, (\alpha, \beta )}({{D}_{j}})}}=\underset{i=1}{\overset{m}{\mathop{\cup }}}\, \overline{{{A}_{i}}^{(\alpha, \beta )}({{D}_{j}})}. $ |
定义6 在决策表S中,A={A1,A2,…, Am}是At的m个属性子集族,则定义Dj的关于属性子集A1,A2,…, Am的悲观-乐观多粒度决策粗糙集模型的下近似和上近似为:
| $ \underline {\sum\limits_{i = 1}^m {A_i^{PO,\left( {\alpha ,\beta } \right)}\left( {{D_j}} \right)} } = \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) \ge \alpha } \right. \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right)\\ \ge \alpha \wedge \cdots \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) \ge \alpha } \right\}; $ |
| $ \begin{array}{l} \overline {\sum\limits_{i = 1}^m {A_i^{PO,\left( {\alpha ,\beta } \right)}\left( {{D_j}} \right)} } = U - \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) \le \beta } \right. \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right)\\ \le \beta \wedge \cdots \wedge p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) \le \beta } \right\} = \\ \left\{ {x \in U\left| {p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_1}}}} \right.} \right) > \beta } \right. \vee p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_2}}}} \right.} \right) > \beta \vee \cdots \vee p\left( {{D_j}\left| {{{\left[ x \right]}_{{A_m}}}} \right.} \right) > \beta } \right\}. \end{array} $ |
性质4 在决策表S中,A={A1,A2,…, Am}是At的m个属性子集族,悲观-乐观多粒度粗糙集模型有下列性质:
| $ 1)\underline{\sum\limits_{i=1}^{m}{{{A}_{i}}^{PO, (\alpha, \beta )}({{D}_{j}})}}=\underset{i=1}{\overset{m}{\mathop{\cap }}}\, \underline{{{A}_{i}}^{(\alpha, \beta )}({{D}_{j}})};2)\overline{\sum\limits_{i=1}^{m}{{{A}_{i}}^{PO, (\alpha, \beta )}({{D}_{j}})}}=\underset{i=1}{\overset{m}{\mathop{\cup }}}\, \overline{{{A}_{i}}^{(\alpha, \beta )}({{D}_{j}})}. $ |
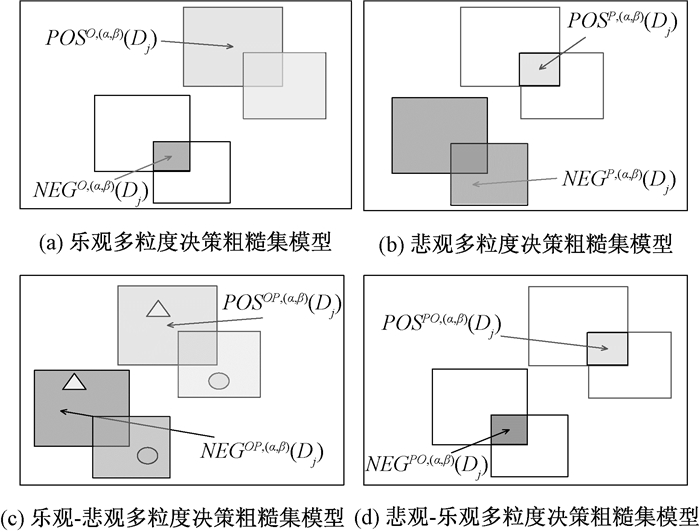
下面主要探讨不同多粒度决策粗糙集模型之间的关系.图 1给出了A={A1, A2}下不同多粒度决策粗糙集模型中Dj-三个概率区域情况.从图 1(c)可以发现,对象1和对象2分别属于粒度A1和A2下正区域.然而,对象1也可能属于粒度A2下负区域,对象2也可能属于A1下负区域.这说明在某些情况下,定义5可能不成立,一些对象可能属于下近似,但不在上近似中.下面通过例1进行说明.
|
图 1 不同多粒度决策粗糙集模型下Dj-三支概率区域 Figure 1 Dj-three probabilistic regions under different multigranulation decision-theoretic rough set models |
例1 假设U={x1, x2, …, x10}是10个评职称的候选人, A={A1, A2}分别表示教学和科研的2个属性子集族,U/A1={{x1, x6}, {x2, x3, x4, x7}, {x5, x9, x10}, {x8}}, U/A2={{x1, x9}, {x2, x3, x4, x10}, {x5, x6, x7}, {x8}}, D1={x1, x2, x3, x7, x10}表示评上职称的候选人.假设α=0.75, β=0.45, D1={x1, x2, x3, x7, x10}, 计算各对象的条件概率如下:
1) 对于属性子集A1,则有
| $ \begin{array}{l} p\left( {{D_1}\left| {{{\left[ {{x_1}} \right]}_{{A_1}}}} \right.} \right) = p\left( {{D_1}\left| {{{\left[ {{x_6}} \right]}_{{A_1}}}} \right.} \right) = 0.5;p\left( {{D_1}\left| {{{\left[ {{x_2}} \right]}_{{A_1}}}} \right.} \right) = p\left( {{D_1}\left| {{{\left[ {{x_3}} \right]}_{{A_1}}}} \right.} \right) \\= p\left( {{D_1}\left| {{{\left[ {{x_4}} \right]}_{{A_1}}}} \right.} \right) = \\ p\left( {{D_1}\left| {{{\left[ {{x_7}} \right]}_{{A_1}}}} \right.} \right) = 0.75;p\left( {{D_1}\left| {{{\left[ {{x_5}} \right]}_{{A_1}}}} \right.} \right) = p\left( {{D_1}\left| {{{\left[ {{x_9}} \right]}_{{A_1}}}} \right.} \right) = p\left( {{D_1}\left| {{{\left[ {{x_{10}}} \right]}_{{A_1}}}} \right.} \right) \\= 0.33;p\left( {{D_1}\left| {{{\left[ {{x_8}} \right]}_{{A_1}}}} \right.} \right) = 0. \end{array} $ |
2) 对于属性子集A2,则有
| $ \begin{array}{l} p\left( {{D_1}\left| {{{\left[ {{x_1}} \right]}_{{A_2}}}} \right.} \right) = p\left( {{D_1}\left| {{{\left[ {{x_9}} \right]}_{{A_2}}}} \right.} \right) = 0.5;p\left( {{D_1}\left| {{{\left[ {{x_2}} \right]}_{{A_2}}}} \right.} \right) \\= p\left( {{D_1}\left| {{{\left[ {{x_3}} \right]}_{{A_2}}}} \right.} \right) = p\left( {{D_1}\left| {{{\left[ {{x_4}} \right]}_{{A_2}}}} \right.} \right) = \\ p\left( {{D_1}\left| {{{\left[ {{x_{10}}} \right]}_{{A_2}}}} \right.} \right) = 0.75;p\left( {{D_1}\left| {{{\left[ {{x_5}} \right]}_{{A_2}}}} \right.} \right) = p\left( {{D_1}\left| {{{\left[ {{x_6}} \right]}_{{A_2}}}} \right.} \right) = p\left( {{D_1}\left| {{{\left[ {{x_7}} \right]}_{{A_2}}}} \right.} \right)\\ = 0.33;p\left( {{D_1}\left| {{{\left[ {{x_8}} \right]}_{{A_2}}}} \right.} \right) = 0. \end{array} $ |
因此,对于D1,4种多粒度决策粗糙集模型的上下近似如表 1所示.表 1和表 2中的OO、PP、OP、PO分别代表乐观-乐观、悲观-悲观、乐观-悲观和悲观-乐观多粒度决策粗糙集模型.
|
|
表 1 4种多粒度决策粗糙集模型的D1-概率区域比较 Table 1 Comparison of D1-probabilistic regions for four multigranulation decision-theoretic rough set models |
从表 1可以看出,乐观-悲观多粒度决策粗糙集模型下近似没有完全包含在上近似中,即对象{x7, x10}既属于正区域,也属于负区域,显然与传统粗糙集模型“上近似一定包含下近似”相矛盾.
例2 (续例1)假设α=0.75, β=0.45, 计算πD-概率区域如表 2所示.
|
|
表 2 4种多粒度决策粗糙集模型的πD-概率区域比较 Table 2 Comparison of πD-probabilistic regions for four multigranulation decision-theoretic rough set models |
从表 2可以发现,乐观多粒度决策粗糙集模型和悲观-乐观多粒度决策粗糙集模型的负区域最小,而悲观多粒度决策粗糙集模型的负区域最大,传统的多粒度决策粗糙集模型的边界域较小.尽管悲观-乐观多粒度决策粗糙集模型的边界域最大,但可以调整α和β进行序贯三支决策.此外,在多粒度决策粗糙集模型中,{x7, x10}是争议对象,仅仅在某个粒度上满足了决策.
性质5 在决策表S中,A={A1, A2, …, Am}是At的m个属性子集族,则下列性质成立:
1)
2)
3)
4)
说明:乐观-悲观多粒度决策粗糙集模型和悲观-乐观多粒度决策粗糙集模型是传统多粒度决策粗糙集模型的补充,为多粒度问题求解提供了另一种视角.例如,在职称评审过程中,可以采用悲观-乐观多粒度决策粗糙集模型,首先选出各方面都优秀的候选人(概率正区域),排除各方面都差的候选人(概率负区域),剩下的候选人(概率边界域)则通过放宽限制条件选出.尽管乐观-悲观多粒度决策粗糙集模型在粗糙集理论中看似不正确,在现实生活中可能是合理的.例如,项目评审可以采用乐观-悲观多粒度决策粗糙集模型,包含在下近似中却没有包含在上近似中的争议项目可能某些方面特别优秀,但存在某个方面不符合要求,这时可以通过协商或专家投票解决.再比如,在研究生招生中,采用乐观-悲观多粒度决策粗糙集模型,可以把有争议的学生进行破格录取.
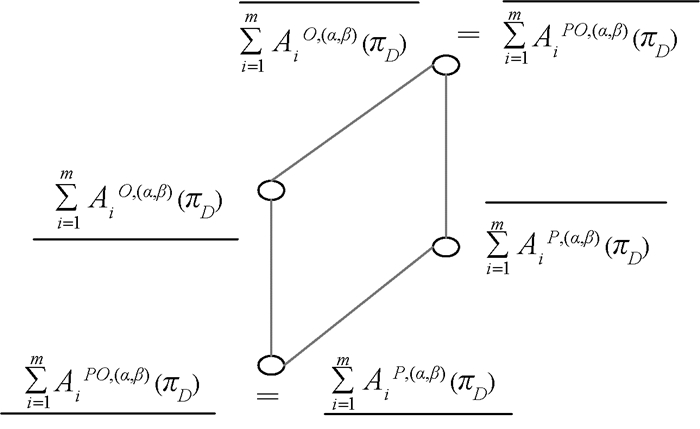
图 2展示了乐观多粒度决策粗糙集模型、悲观多粒度决策粗糙集模型以及悲观-乐观多粒度决策粗糙集模型3者之间的关系.
|
图 2 3种多粒度决策粗糙集模型之间关系 Figure 2 Relationships among three multigranulation decision-theoretic rough set models |
通过剖析传统多粒度决策粗糙集模型,提出了乐观-悲观和悲观-乐观两种多粒度决策粗糙集模型,分析了这两种模型的正确性和合理性,比较了不同多粒度决策粗糙集模型之间的关系,使得决策粗糙集模型适合更多的多粒度环境.目前,多粒度决策粗糙集模型中不同粒度都采用单一阈值,不太适合处理多源异构数据集.作者下一步工作主要研究多阈值的多粒度决策粗糙集模型.
| [1] |
PAWLAK Z. Rough sets[J]. International journal of computer and information sciences, 1982, 11(2): 341-356. (  0) 0) |
| [2] |
YAO Y Y. A decision theoretic framework for approximating concepts[J]. International journal of man-machine studies, 1992, 37(6): 793-809. DOI:10.1016/0020-7373(92)90069-W (  0) 0) |
| [3] |
CHEN H M, LI T R, LUO C, et al. A decision-theoretic rough set approach for dynamic data mining[J]. IEEE transactions on fuzzy systems, 2015, 23(6): 1958-1970. DOI:10.1109/TFUZZ.2014.2387877 (  0) 0) |
| [4] |
YU H, JIAO P, YAO Y Y, et al. Detecting and refining overlapping regions in complex networks with three-way decisions[J]. Information sciences, 2016, 373: 21-41. DOI:10.1016/j.ins.2016.08.087 (  0) 0) |
| [5] |
ZHANG H R, MIN F. Three-way recommender systems based on random forests[J]. Knowledge-based systems, 2016, 91: 275-286. DOI:10.1016/j.knosys.2015.06.019 (  0) 0) |
| [6] |
LI H X, ZHANG L B, HUANG B, et al. Sequential three-way decision and granulation for cost-sensitive face recognition[J]. Knowledge-based systems, 2016, 91: 241-251. DOI:10.1016/j.knosys.2015.07.040 (  0) 0) |
| [7] |
CHEN J, ZHANG Y P, ZHAO S. Multi-granular mining for boundary regions in three-way decision theory[J]. Knowledge-based systems, 2016, 91: 287-292. DOI:10.1016/j.knosys.2015.10.020 (  0) 0) |
| [8] |
LI J H, HUANG C C, QI J J, et al. Three-way cognitive concept learning via multi-granularity[J]. Information sciences, 2017, 378: 244-263. DOI:10.1016/j.ins.2016.04.051 (  0) 0) |
| [9] |
QIAN Y H, ZHANG H, SANG Y L, et al. Multigranulation decision-theoretic rough sets[J]. International journal of approximate reasoning, 2014, 55(1): 225-237. DOI:10.1016/j.ijar.2013.03.004 (  0) 0) |
| [10] |
LI W T, XU W H. Multi-granulation decision-theoretic rough set in ordered information system[J]. Fundamenta informaticae, 2015, 139(1): 67-89. DOI:10.3233/FI-2015-1226 (  0) 0) |
| [11] |
YANG H L, GUO Z L. Multi-granulation decision-theoretic rough sets in incomplete information systems[J]. International journal of machine learning and cybernetics, 2015, 6(6): 1005-1018. DOI:10.1007/s13042-015-0407-9 (  0) 0) |
| [12] |
LIU C H, PEDRYCZ W, WANG M Z. Covering-based multigranulation decision-theoretic rough sets[J]. Journal of intelligent and fuzzy systems, 2017, 32(1): 749-765. (  0) 0) |
| [13] |
FENG T, MI J S. Variable precision multigranulation decision-theoretic fuzzy rough sets[J]. Knowledge-based systems, 2016, 91: 93-101. DOI:10.1016/j.knosys.2015.10.007 (  0) 0) |
| [14] |
SUN B Z, MA W M, XIAO X. Three-way group decision making based on multigranulation fuzzy decision-theoretic rough set over two universes[J]. International journal of approximate reasoning, 2017, 81: 87-102. DOI:10.1016/j.ijar.2016.11.001 (  0) 0) |
| [15] |
LIN G P, LIANG J Y, QIAN Y H, et al. A fuzzy multigranulation decision-theoretic approach to multi-source fuzzy information systems[J]. Knowledge-based systems, 2016, 91: 102-113. DOI:10.1016/j.knosys.2015.09.022 (  0) 0) |
| [16] |
薛占熬, 袁艺林, 辛现伟, 等. 多粒度广义L-模糊可变精度粗糙集[J]. 郑州大学学报(理学版), 2016, 48(3): 82-89. (  0) 0) |
| [17] |
XU W H, GUO Y T. Generalized multigranulation double-quantitative decision-theoretic rough set[J]. Knowledge-based systems, 2016, 105: 190-205. DOI:10.1016/j.knosys.2016.05.021 (  0) 0) |
| [18] |
YANG X B, QI Y S, SONG X N, et al. Test cost sensitive multigranulation rough set: model and minimal cost selection[J]. Information sciences, 2013, 250: 184-199. DOI:10.1016/j.ins.2013.06.057 (  0) 0) |
| [19] |
HU B Q. Three-way decision space and three-way decisions[J]. Information sciences, 2014, 281: 21-52. DOI:10.1016/j.ins.2014.05.015 (  0) 0) |
| [20] |
YANG X P, YAO J T. Modelling multi-agent three-way decisions with decision-theoretic rough sets[J]. Fundamenta informaticae, 2012, 115(2/3): 157-171. (  0) 0) |
| [21] |
ZHANG X H, MIAO D Q, LIU C H, et al. Constructive methods of rough approximation operators and multigranulation rough sets[J]. Knowledge-based systems, 2016, 91: 114-125. DOI:10.1016/j.knosys.2015.09.036 (  0) 0) |
 2018, Vol. 50
2018, Vol. 50

