实际生活中很多情形都可以归结为钝体绕流问题, 如河流绕过桥墩的流动以及建筑物的风载等.流体流经钝体时, 由于过流界面减小, 会产生一系列复杂的物理现象, 特别是边界层的分离进而在钝体后产生周期脱落的涡.目前钝体绕流研究主要以圆柱绕流为主, 对于一般形状柱体的研究还更多的处于实验阶段.
对于复杂流体绕流, 传统的CFD方法是从宏观Navier-Stokes方程出发, 利用各种数值方法进行模拟.文献[1]分别使用有限差分法和离散涡方法计算了低雷诺数和高雷诺数下的方柱绕流;文献[2]通过有限元法求解了2个圆柱左右并排时和前后排列时的绕流.格子Boltzmann方法作为一种介观模拟方法, 将宏观运动和微观运动的统计平均联系起来, 在流体力学问题的数值模拟方面具有广阔的前景.格子Boltzmann方法不但可以方便地模拟复杂几何形状边界的流体流动, 还可以模拟系统的时间演化, 并且只需要简单的算法就可以在计算机上实现并行计算, 具有更高的计算效率.本文利用格子Boltzmann方法对不同雷诺数下固定单方柱绕流流场进行分析, 并对并列双方柱不同分布间距的流场进行了模拟, 验证了格子Boltzmann方法边界处理和数值模拟的正确性和便捷性.
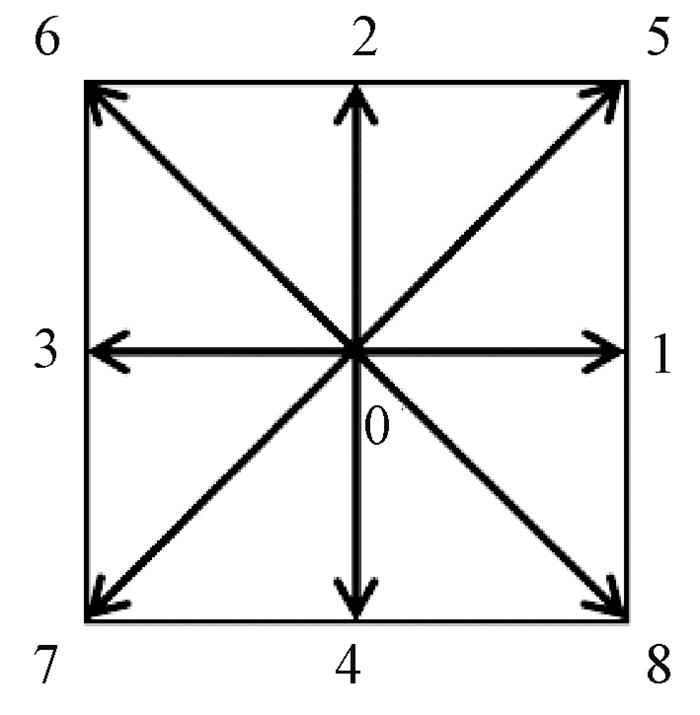
1 格子Boltzmann方法格子Boltzmann方法中的基本变量是格点的分布函数fi, fi为沿i方向的粒子分布函数.本文采用D2Q9模型, 9个离散速度分布如图 1所示.其演化方程(不含外力项)为
|
图 1 D2Q9模型离散速度 Figure 1 Discrete velocities of D2Q9 model |
| $ {f_i}(x + {c_i}\Delta t, t + \Delta t) - {f_i}\left( {x, t} \right) = - \frac{{\Delta t}}{\tau }[{f_i}\left( {x, t} \right) - f_i^{{\rm{eq}}}\left( {x, t} \right)], $ |
式中:Δt为时间步长;τ为无量纲松弛时间, τ=τ0/Δt;离散速度ci表示粒子的运动方向, 可以表示为
| $ {c_0} = \left( {0, 0} \right), {c_{1, 3}}, {c_{2, 4}} = \left( { \pm c, 0} \right), \left( {0, \pm c} \right), {c_{5, 6}}, {c_{7, 8}} = \left( { \pm c, c} \right), \left( {c, \pm c} \right), $ |
其中:c为当地声速.局部平衡态分布函数fieq(x, t)仅与当地的密度和动量有关, 由熵增加原理推出, 可以表示为
| $ f_i^{{\rm{eq}}} = \rho {\omega _i}[1 + \frac{{{c_i} \cdot u}}{{{R_g}T}} + \frac{{{{({c_i} \cdot u)}^2}}}{{2R_g^2{T^2}}} + \frac{{{u^2}}}{{2{R_g}T}}] + o({u^3}). $ |
由平衡态分布函数通过Chapman Enskog展开, 可以导出模型的宏观密度和宏观速度分别为
| $ \rho = \sum\limits_i {{f_i}, u} = \frac{1}{\rho }\sum\limits_i {{f_i}{c_i}} . $ |
格子Boltzmann方法在物理空间上将系统粒子运动分为迁移和碰撞两个相对独立的过程, 使其具备很好的并行特性以及较强的复杂边界处理能力.
2 格子Boltzmann方法的初始条件和边界格式处理流体的运动总是在一定的初始条件和边界条件下进行的, 因此必须设置相应的初始条件和边界条件.格子Boltzmann方法中的基本变量是分布函数.对于稳态或者准稳态流动, 初始条件对最终计算结果影响不大, 可以直接将初始分布函数设为其平衡态分布函数.实际问题中, 边界条件往往基于宏观物理量, 如何根据宏观量合理地确定分布函数是格子Boltzmann方法中的重要问题.常用的边界主要分为启发格式边界、动力学格式边界、外推格式边界以及复杂格式边界;根据实际问题又可分为速度边界和压力边界等.
2.1 非平衡态外推格式边界借鉴了传统计算流体力学方法(如有限差分法)中的边界处理方法, 文献[3]在此基础上提出了非平衡态外推格式, 将边界节点xb上的分布函数分解为平衡态和非平衡态两部分, 即fi, xb=fi, xbeq+fi, xbne, i=2, 5, 6.平衡态函数中用临近流体点xf的密度ρf代替壁面密度ρw, 而非平衡态部分则使用临近流体点xf的非平衡态部分进行近似, 即fi, xbne=fi, xfne=fi, xf-fi, xfne, i=2, 5, 6.理论研究结果表明, 非平衡态外推格式具有二阶精度.
2.2 非平衡态反弹格式边界实际应用中, 边界处的速度分量或者压力分布往往是已知的, 如管道流动等.文献[4]在1997年提出的非平衡态反弹格式则可以很好地应用于上述两种边界条件.对于速度边界条件, 有
| $ \left\{ \begin{array}{l} {\rho _w} = \frac{1}{{1 - {u_w}}}[{f_0} + {f_2} + {f_4} + ({f_3} + {f_6} + {f_7})], \\ {\rm{ }}{f_1} = {f_3} + \frac{2}{3}{\rho _w}{u_w}, \\ {\rm{ }}{f_5} = {f_7} - \frac{1}{2}({f_2} - {f_4}) + \frac{1}{6}{\rho _w}{u_w} + \frac{1}{2}{\rho _w}{v_w}, \\ {\rm{ }}{f_8} = {f_6} + \frac{1}{2}({f_2} - {f_4}) + \frac{1}{6}{\rho _w}{u_w} - \frac{1}{2}{\rho _w}{v_w}. \end{array} \right. $ |
通过非平衡态反弹格式可以直接计算垂直于速度边界上的3个未知平衡态分布函数, 相似的方法也可以用于压力边界和其他边界条件.
3 固定方柱绕流的数值模拟与分析 3.1 单方柱绕流模拟柱体绕流是一类经典的非定常流体力学问题, 数值模拟是这类问题最有力的研究工具.大量理论研究结果表明, 柱体绕流中对流场起决定性作用的参数是雷诺数(Re). Re不同, 黏性不可压缩流体会呈现不同的流体状态.本文采用单松弛(LBGK)模型, 利用C++语言对单方柱绕流问题进行计算机模拟, 研究不同Re对方柱绕流状态的影响.图 2为单方柱绕流模型示意图.可以看出, 模型长宽比为3:1, 入口采用非平衡态反弹格式速度边界, 入口速度为均匀来流U=0.1;出口采用非平衡态反弹格式压力边界(设出口密度为1.0), 方柱表面和管道上下壁面则采用非平衡态外推格式.此处, 雷诺数

|
图 2 单方柱绕流模型示意图 Figure 2 Schematic diagram of channel flow past a single square cylinder |
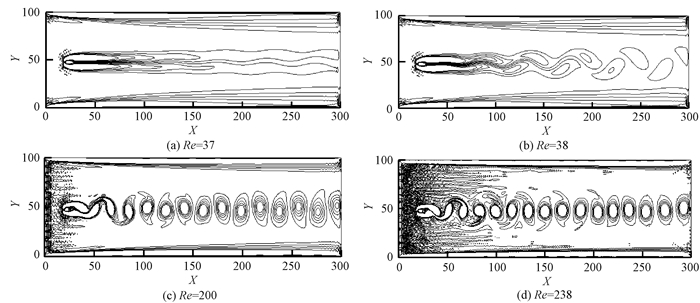
图 3为不同雷诺数下流场涡量云图.可以看出, 当Re较小时, 流场是定常的, 方柱后面出现一对上下对称的尾涡.随着Re的增加, 当Re=38时, 流场逐渐转变为非定常, 尾涡也逐渐脱落, 尾流区中形成周期性摆动和交错的漩涡, 即出现卡门涡街.随着Re的进一步增加, 当Re=238时, 尾涡有紊乱的趋势.进一步的模拟显示, 当Re大于238时, 尾流区由层流状态过渡到紊流状态.
|
图 3 不同雷诺数下流场涡量云图 Figure 3 Vorticity contours at different Reynolds numbers |
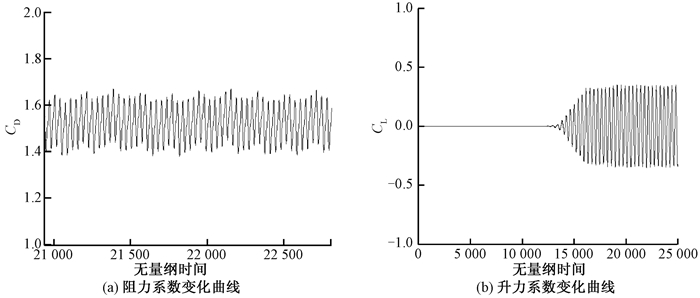
图 4显示了Re=200时阻力系数和升力系数随时间的变化曲线, 当前平均阻力系数和最大升力系数分别为1.51和0.31, 与文献[5]中实验研究的数据相比具有一致性, 可见利用格子Boltzmann方法模拟是可行的.
|
图 4 Re=200时阻力系数和升力系数随时间的变化曲线 Figure 4 Time history of drag coefficient and lift coefficient at Re=200 |
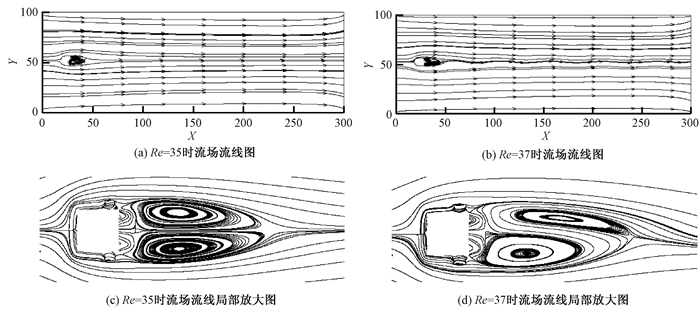
Re=35及Re=37时的流场流线分析如图 5所示, 可以看出, 上下对称的尾涡逐渐扩大, 上涡有分离的趋势.因此, 定常流失稳的临界Re在37左右, 这与文献[6]中的结论是相符合的.
|
图 5 不同雷诺数下流场流线图 Figure 5 Streamline patterns at different Reynolds numbers |
与理论研究及文献中圆柱绕流的结果对比后发现, 方柱绕流整体上符合一般的钝体绕流趋势, 并且由于方柱的特殊性, 临界Re又与圆柱绕流不同.由以上分析可知, 方柱绕流中卡门涡街现象在Re为40~238时较为明显.本文将采用Re=200进行下一步的模拟研究.
3.2 双方柱绕流模拟实际生活中更多的是流体绕过多个柱体流动的情形, 柱体的个数、形状、排列方式等均会影响流场的结构.本文研究双方柱并列模型下不同分布间距对流场的影响, 控制的变量为柱间距M与方柱特征尺寸H的比值(M/H), 并列双方柱绕流模型示意图如图 6所示.

|
图 6 并列双方柱绕流模型示意图 Figure 6 Schematic diagram of channel flow past parallel square cylinders |
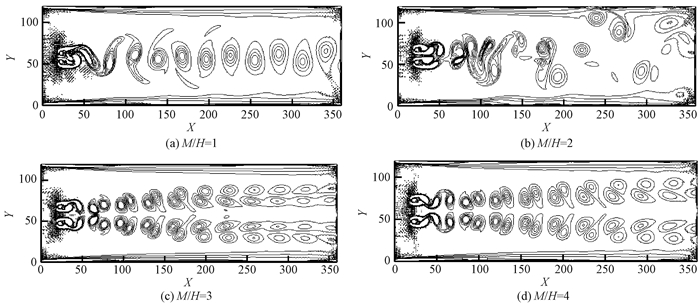
采用相同的边界条件, X、Y方向格子数分别为360和120, 在Re=200的条件下分别对并列方柱M/H=1、M/H=2、M/H=3、M/H=4四种条件进行模拟, 其涡量云图如图 7所示.
|
图 7 不同分布间距下流场涡量云图 Figure 7 Vorticity contours at different distribution distances |
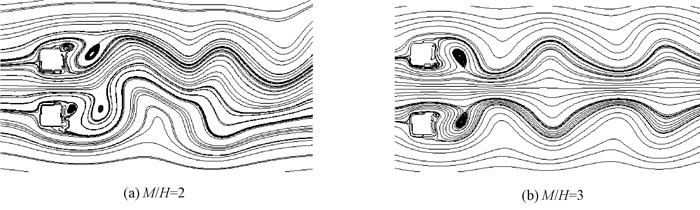
图 8显示了并列方柱在M/H=2和M/H=3时的流场流线图.从图 7和图 8中可以看出, 当分布间距较小(M/H=1)时, 两柱形成的漩涡彼此影响较小, 还保留着部分单柱绕流的流场特征;随着分布间距的增加, 流场逐渐变得复杂, 漩涡分布呈现不规则状态, 当M/H=2时, 流体绕流方柱的涡流彼此影响最为明显;分布间距继续增加, 当M/H大于3时, 两个涡的相互影响越来越小, 方柱下游形成两个反向同步脱落的涡街, 各自涡形逐渐接近单方柱卡门涡街状态.
|
图 8 不同分布间距下流场流线图 Figure 8 Streamline patterns at different distribution distances |
通过对单方柱和并列双方柱的模拟研究, 验证了格子Boltzmann方法边界处理和数值模拟的正确性和便捷性.通过对不同Re下单方柱流场的模拟分析, 探究了方柱产生卡门涡街的临界雷诺数(Re=37), 并得到了产生明显卡门涡街的雷诺数范围(Re=40~238).此外, 雷诺数Re=200下并列双方柱不同分布间距(M/H=1、M/H=2、M/H=3、M/H=4)的流场模拟结果表明, 当柱间距为2倍方柱边长时, 流体绕流方柱的涡流彼此影响最为明显.
| [1] |
OKAJIMA A. Numerical simulation of flow around rectangular cylinders[J]. Journal of wind engineering and industrial aerodynamics, 1990, 33(1): 171-180. (  0) 0) |
| [2] |
MENEGHINI J R, SALTARA F, SIQUEIRA C L R, et al. Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements[J]. Journal of fluids and structures, 2001, 15(2): 327-350. DOI:10.1006/jfls.2000.0343 (  0) 0) |
| [3] |
GUO Z L, ZHENG C G, SHI B C. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method[J]. Chinese physics B, 2002, 11(4): 366-374. DOI:10.1088/1009-1963/11/4/310 (  0) 0) |
| [4] |
ZOU Q S, HE X Y. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model[J]. Physics of fluids, 1997, 9(6): 1591-1598. DOI:10.1063/1.869307 (  0) 0) |
| [5] |
SAHA A K, BISWAS G, MURALIDHAR K. Three-dimensional study of flow past a square cylinder at low Reynolds numbers[J]. International journal of heat and fluid flow, 2003, 24(1): 54-66. DOI:10.1016/S0142-727X(02)00208-4 (  0) 0) |
| [6] |
周云龙, 邓冬, 刁成东, 等. 方柱绕流和圆柱绕流旋涡脱落的数值模拟[C]//中国工程热物理学会多相流学术会议. 青岛, 2008: 1-6. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=6846247
(  0) 0) |
 2018, Vol. 50
2018, Vol. 50


