2. 山西大学 计算智能与中文信息处理教育部重点实验室 山西 太原 030006
2. Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education, Shanxi University, Taiyuan 030006, China
以微博为代表的社交网络的兴起使得每一个网民都能自由地表达自身的观点、态度、情感等主观性信息.截至2015年12月,我国微博用户规模为2.04亿.分析和监测微博所包含的情感信息,能够了解广大网民对某产品、人物或者事件的关注程度和情感变化,为决策者提供实时科学的理论依据,具有巨大的商业价值和社会价值,也给自然语言处理(NLP)带来了新的机遇和挑战.
微博观点句情感分析的主要目的就是从用户发布的微博中识别含有观点的句子,并判断其情感极性.目前研究主要集中于基于人工特征工程和基于机器学习的方法.基于人工特征工程的方法通常采用情感词典和规则相结合,通过在已有的词典或知识库资源进行一定的扩展生成情感倾向词典,或是预先建立一个倾向性语义规则集,进而实现对文本的情感识别.例如,文献[1]提出一种整合语言学现象、常识推理的概念层的情感分析方法.基于机器学习的方法通常是将情感分析问题看作是一个分类问题,标注好的训练集通过机器学习算法,以情感词、主题相关特征等作为分类特征训练得到分类模型,用于以后的情感分类.例如,文献[2]在Twitter数据集上实现了基于朴素贝叶斯、支持向量机和条件随机场的情感分类器,取得了良好的效果.
近年来,深度学习成为NLP领域最热门的研究之一.对于句子的表示学习,主要有使用词表示的组合和直接学习句子的分布两种方法.卷积神经网络(CNN)[3-4]是一种有效的对句子进行建模的方法,其核心就是对语言片段中出现的词进行窗口平滑,利用平滑后句子向量进行后续的NLP相关研究.文献[5]使用递归循环神经网络(RNN)训练句子表示,RNN剔除了窗口限制,可以充分利用所有上文信息来预测下一个词.文献[6]通过将句子ID号作为一个输入单元训练,以学习到的向量作为该句子的表示.文献[7]使用深度置信网,从自动标注的语料集中学习句向量作为独立的补充特征,可用于微博情绪分类.针对传统以词为基本单元的方法在对语言表达建模上存在精度刻画不足的问题,文献[8-9]在英文字符级粒度上进行语言建模,这类工作使用字符级的n-gram,并使用CNN学习其特征表示,提高了在语音识别和文本分类上的效果.文献[10]在词向量的基础上,联合学习了汉字向量,并设计了基于位置和基于聚类的字向量学习方法,将字向量作为词向量的额外补充信息.这类方法仍是以词作为主要建模对象,字符表示仅仅作为词的补充信息.
本文提出了基于增强字向量的微博观点句情感极性分类方法,使用单字作为句子表示的基本单元,同时在单字中嵌入了该字所在的词信息以及该词的词性信息,以此训练得到字向量替代传统的词向量融合的句子表示方法.利用给定的样例集信息,使用K-means聚类对向量化的句子进行情感判定.该方法仅需要对文本进行分词和词性标注,无需额外的语言学资源.
1 基于增强字向量的观点句分类使用合适的句子表示方法是句子级情感分析的核心.传统基于词袋模型或词向量的方法以词为基本单元进行建模,忽略了更细粒度的字之间含有的语言信息.本文提出了基于增强字向量(enhanced-character vector, ECV)的微博观点句情感极性分类方法.
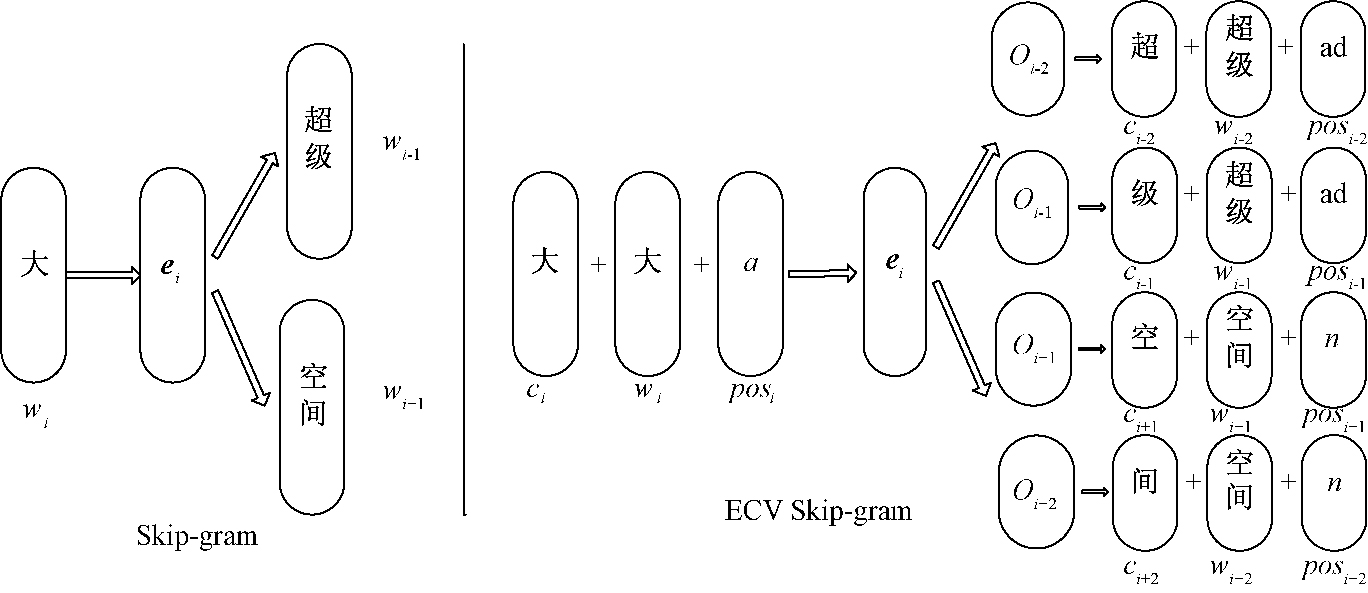
1.1 增强字向量训练借助Google的Word2vec开源词向量工具,选用基于霍夫曼编码的Skip-gram神经网络模型[11-12]为基础进行改造,提出了基于ECV的训练框架,该框架与Skip-gram模型的关系如图 1所示.
|
图 1 Skip-gram 与ECV Skip-gram的关系 Figure 1 Relationship between Skip-gram and ECV Skip-gram |
给定一个词wi,Skip-gram模型首先将其映射成一个连续向量ei,使用该映射来预测词wi的上下文窗口内的词语wi-n, …,wi-1, wi+1, …, wi+n,2n为窗口大小.优化目标是最大化如下的对数似然:
| $ L = \sum\limits_{{w_i} \in C} {\log p\left( {Context\left( {{w_i}} \right)\left| {{w_i}} \right.} \right)} = \sum\limits_{{w_i} \in C} {\sum\limits_{u \in Context\left( {{w_i}} \right)} {\log p\left( {u\left| {{w_i}} \right.} \right)} } , $ | (1) |
其中:
| $ \log p\left( {u\left| {{w_i}} \right.} \right) = \sum\limits_{j = 2}^{{l^u}} {\log p\left( {d_j^u\left| {{\mathit{\boldsymbol{e}}_{{w_i}}},\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right.} \right)} , $ | (2) |
式中:dju表示该词u在其路径上第j个节点的编码;θj-1u表示路径上非叶子节点对应的参数向量;lu表示从霍夫曼树的根节点到词u的路径长.在霍夫曼树中,将一个节点分到左侧为负类,分到右侧为正类.即有
| $ p\left( {d_j^u\left| {{\mathit{\boldsymbol{e}}_w},\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right.} \right) = \left\{ \begin{array}{l} \sigma \left( {\mathit{\boldsymbol{e}}_w^{\rm{T}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right),d_j^u = 0,\\ 1 - \sigma \left( {\mathit{\boldsymbol{e}}_w^{\rm{T}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right),d_j^u = 1, \end{array} \right. $ | (3) |
式中:σ为Sigmoid函数.在Word2vec的代码实现中,由输入向量v(wi)→e(wi)的映射采用的是恒等映射,即v(wi)=e(wi),因此(2)式可以等价为
| $ \log p\left( {u\left| {{w_i}} \right.} \right) = \sum\limits_{j = 2}^{{l^u}} {\log p\left( {d_j^u\left| {\mathit{\boldsymbol{v}}\left( {{w_i}} \right),\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right.} \right)} , $ | (4) |
为使该模型适应以字向量为基本单元的需要,文本的输入为三元组ti=〈ci,wi,posi〉, 映射函数设置为
| $ \mathit{\boldsymbol{e}}\left( {{t_i}} \right) = concatenate\left( {{\mathit{\boldsymbol{V}}_{{c_i}}},{\mathit{\boldsymbol{V}}_{{w_i}}},{\mathit{\boldsymbol{V}}_{po{s_i}}}} \right). $ | (5) |
将式(3)、(5)代入式(2)并展开,得
| $ \begin{array}{l} \log p\left( {u\left| {{t_i}} \right.} \right) = \sum\limits_{j = 2}^{{l^u}} {\log p\left( {d_j^u\left| {\mathit{\boldsymbol{e}}\left( {{t_i}} \right),\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right.} \right)} = \\ \sum\limits_{j = 2}^{{l^u}} {\log \left\{ {{{\left[ {\sigma \left( {\mathit{\boldsymbol{e}}{{\left( {{t_i}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right)} \right]}^{1 - d_j^u}} \cdot {{\left[ {1 - \sigma \left( {\mathit{\boldsymbol{e}}{{\left( {{t_i}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right)} \right]}^{d_j^u}}} \right\}} = \\ \sum\limits_{j = 2}^{{l^u}} {\left\{ {\left( {1 - d_j^u} \right)\log \left[ {\sigma \left( {\mathit{\boldsymbol{e}}{{\left( {{t_i}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right)} \right] + d_j^u\log \left[ {1 - \sigma \left( {\mathit{\boldsymbol{e}}{{\left( {{t_i}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right)} \right]} \right\}} . \end{array} $ | (6) |
整个模型的对数似然函数为
| $ L = \sum\limits_{{w_i} \in C} {\sum\limits_{u \in Context\left( w \right)} {\sum\limits_{j = 2}^{{l^u}} {\left\{ {\left( {1 - d_j^u} \right)\log \left[ {\sigma \left( {\mathit{\boldsymbol{e}}{{\left( {{t_i}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right)} \right] + d_j^u\log \left[ {1 - \sigma \left( {\mathit{\boldsymbol{e}}{{\left( {{t_i}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right)} \right]} \right\}} } } . $ | (7) |
使用梯度上升法计算该对数似然的优化,有
| $ \begin{array}{l} \frac{{\partial L}}{{\partial \mathit{\boldsymbol{\theta }}_{j - 1}^u}} = \left[ {1 - d_j^u - \sigma \left( {\mathit{\boldsymbol{e}}{{\left( {{t_i}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right)} \right]\mathit{\boldsymbol{e}}\left( {{t_i}} \right);\\ \frac{{\partial L}}{{\partial \mathit{\boldsymbol{e}}\left( {{t_i}} \right)}} = \sum\limits_{u \in Context\left( {{t_i}} \right)} {\sum\limits_{j = 2}^{{l^u}} {\left[ {1 - d_j^u - \sigma \left( {\mathit{\boldsymbol{e}}{{\left( {{t_i}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right)} \right]\mathit{\boldsymbol{\theta }}_{j - 1}^u} } . \end{array} $ | (8) |
因此,参数更新公式为
| $ \mathit{\boldsymbol{\theta }}_{j - 1}^u: = \mathit{\boldsymbol{\theta }}_{j - 1}^u + \eta \left[ {1 - d_j^u - \sigma \left( {\mathit{\boldsymbol{e}}{{\left( {{t_i}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right)} \right]\mathit{\boldsymbol{e}}\left( {{t_i}} \right), $ | (9) |
| $ \mathit{\boldsymbol{e}}\left( {{t_i}} \right): = \mathit{\boldsymbol{e}}\left( {{t_i}} \right) + \eta \sum\limits_{u \in Context\left( {{t_i}} \right)} {\sum\limits_{j = 2}^{{l^u}} {\left[ {1 - d_j^u - \sigma \left( {\mathit{\boldsymbol{e}}{{\left( {{t_i}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\theta }}_{j - 1}^u} \right)} \right]\mathit{\boldsymbol{\theta }}_{j - 1}^u} } . $ | (10) |
因为输入向量三元组ti分别由字向量、词向量和词性向量拼接而成,每次迭代完成后,对于得到的上下文向量V(u)也是ti的上下文三元组向量.可以通过将V(u)分别与一个对应位置为1,其余为0的0-1向量作内积截取得到ti中的字、词、词性向量表示.而在实际实验中,因为只需使用三元组ti拼接后的向量表示信息,同时也为了加快模型的训练速度,在初始对每个三元组单元ti随机赋值后,在模型迭代过程中将直接使用三元组ti的向量作为下一次迭代的输入,不再进行拼接与截取操作.
1.2 基于boostrapping的主题词扩展算法由于微博文本具有开放性,利用给定小规模样例中的对象词作为种子集,使用bootstrapping算法扩展主题词集合,以滤除主题无关的句子.扩展算法(算法1)如下:
Input: 初始种子主题词集Sseed,全语料词集Sall;
Output: 扩展主题词集Swt.
1: Initialize Swt=Sseed
2: for each word wi in Sall
3: for each word wtj in Swt
4: if wi∈k-NN(wtj) and sim(wtj,wi)≥α
5: Swt=Swt∪{wi}
6: Sall =Sall/{wi}
7: end if
8: end for
9: end for
10: repeat steps 2~9 until Swt no longer change
算法1中k-NN(wtj) 为与种子词wtj最相似的k词集合,sim(wtj,wi)表示候选词wi与种子词wtj之间的相似度,α为给定阈值参数.经过扩展的主题词词典可以有效过滤掉部分主题无关句子,同时可以为观点句表示提供额外的主题信息.
1.3 观点句表示经过1.1训练得到的字向量,需要对其进行组合以表示句子向量.同时,为了加强主题词的权重,将主题词的词向量拼接到句向量中,句子的向量表示为
| $ {\mathit{\boldsymbol{V}}_{sk}} = concatenate\left( {\frac{1}{n}\sum\limits_{i = 1}^n {{\mathit{\boldsymbol{V}}_{{c_{ki}}}}} ,\frac{1}{m}\sum\limits_{j = 1}^n {{\mathit{\boldsymbol{V}}_{w{t_{kj}}}}} } \right),{c_{ki}} \in \left\{ {{c_k}} \right\},w{t_{kj}} \in \left\{ {w{t_k}} \right\}, $ | (11) |
式中:{ck}、{wtk}分别为句子Sk中包含的字集和主题词集.
1.4 基于K-means的观点句极性判别算法使用K-means聚类方法判定观点句的情感极性,用给定小规模样例中的句子情感标签提供初始的情感信息,分别以各情感标签下句子向量的均值作为初始聚类中心.基于K-means的观点句极性判别算法(算法2)如下:
Input: 初始样例句子向量集 Ssample, 待分类句子向量集S;
Output: 分类句子集
1: Initialize cluster center
2: for each sentence Si in S
3: if max(sim(VSj, VCi))≥β
4: Label(Sj)=argmaxi(sim(VSj, VCi))
5: {LLabel(Sj)}={LLabel(Sj)}∪{Sj}
6: S=S/{Sj}
7: end if
8: end for
9: update cluster center {VCi}i=1K={AVG(VLi)}i=1K
10: repeat steps 2~9 until {Li}i=1K no longer change
算法2中Ssample-i表示样例句子集中类别标签为i的句子,AVG(·)为取向量均值函数,K为类别标签个数,β为待测阈值参数.
2 数据与实验 2.1 数据集使用COAE2015任务2提供的微博句子语料[13]进行实验.该任务是给定较大规模的微博句子集,要求参赛系统识别其中的观点句并判定观点极性.语料规模共计文本50 000篇,133 202条句子,涉及手机、美食、汽车、新闻、娱乐等领域.
2.2 实验与结果分析根据算法1和算法2可知,α和β取值越大,则识别出的观点句精确率越高,反之召回率越高.经过多次实验综合考虑,将参数设为α=0.5,β=0.4.具体过程如下:
1) 使用ICTCLAS对所有句子进行基础分词.
2) 以给定样例中的对象词为种子集,使用Word2vec学习得到种子集和待测数据中词语的词向量.为使训练的词向量更加精确,在COAE2015任务2数据集的基础上,额外加入了COAE2014任务3的1 000万条无标签微博数据,合并进行学习.得到词语的词向量后,根据1.2节扩展主题词集Swt.
3) 利用Swt对任务数据集进行筛选,得到63 716句.
4) 利用1.1节在全部任务数据上使用Word2vec学习增强字向量.
5) 利用1.3节得到3)中句子的向量表示.
6) 使用1.4节的算法对句子进行情感极性判定.
本文方法参与了COAE2015任务2评测,实验结果如表 1所示.可以看出,本文方法在限定资源使用的提交答案中处于中上水平,其中宏平均F1值在全部18个run中排名第4.分析结果发现:① 本文结果中召回率与最好值差距较大.原因是本次评测不限制各单位提交的结果数,提交结果共计6万余条,相对其他单位提交结果较少,一定程度上使得本文召回率相对较低.② 对于混合情感极性的结果相对较差.一方面说明基于字向量方法对于混合情感类的句子相对欠缺,另一方面由于给定样例中混合句子比例过少(占全部样例的14%),使得初始聚类中心并不准确.③ 准确率与最好值相比还有一些不足.主要是因为本文是以单字为基础单元,相比词汇级粒度其多义性问题更加严重.在后续的实验中尝试加入了单字所属词的情感极性特征,然而其分类效果不升反降,是由于在单字组词过程中,其有较高概率同时出现在褒义词和贬义词中,使得加入的情感特征对于单字表示产生了负面影响,特别是对混合情感的判定尤为明显.此外,在实验中发现,在全部句子中显示含有限定情感词典中的情感词的句子只有约1万句,大部分句子无法通过情感词典获得有效的情感信息.
|
|
表 1 实验结果 Table 1 The experimental result |
提出了基于增强字向量的微博观点句情感极性分类方法,使用单字作为句子表示的基本单元,同时在单字中嵌入了该字所在的词信息以及该词的词性信息,以此训练得到字向量替代传统的词向量融合的句子表示方法.利用给定的样例集信息,使用K-means聚类对向量化的句子进行情感判定.在COAE2015任务2数据集上的实验结果表明,基于字向量的观点句情感极性分类具有一定的可行性.
在未来的工作中,针对性地解决单字的多义性问题,将归属于不同语义、情感的单字分别学习其表示,而不仅仅以所属词汇进行区分,以达到更精准的表示效果.同时,任务数据为开放领域,而本文方法利用了给定的小规模样例数据集提供初始主题种子和情感信息,样例信息的不完备对最终结果有一定影响.此外,本次评测数据是以篇章-句子二级粒度的形式,在今后的工作中还需要充分考虑篇章内的上下文信息,进一步完善对于混合情感句的识别方法.
| [1] |
PORIA S, CAMBRIA E, WINTERSTEIN G, et al. Sentic patterns:dependency-based rules for concept-level sentiment analysis[J]. Knowledge-based systems, 2014, 69(1): 45-63. (  0) 0) |
| [2] |
PAK A, PAROUBEK P. Twitter as a corpus for sentiment analysis and opinion mining[C]//Proceedings of the International Conference on Language Resources and Evaluation. Stroudsburg,2010:1320-1326.
(  0) 0) |
| [3] |
BLUNSOM P, GREFENSTETTE E, KALCHBRENNER N. A convolutional neural network for modelling sentences[C]//Proceedings of 52nd Annual Meeting of the Association for Computational Linguistics. Stroudsburg,2014:655-665.
(  0) 0) |
| [4] |
KIM Y. Convolutional neural networks for sentence classification[C]//Proceedings of the Conference on Empirical Methods in Natural Language Processing. Stroudsburg, 2014:1746-1751.
(  0) 0) |
| [5] |
MIKOLOV T, KARAFIÁT M, BURGET L, et al. Recurrent neural network based language model[C]//Proceedings of 11th Annual Conference of the International Speech Communication Association.Chiba, 2010:1045-1048.
(  0) 0) |
| [6] |
LE Q V, MIKOLOV T. Distributed representations of sentences and documents[C]//Proceedings of the 31st International Conference on Machine Learning. New York, 2014:1188-1196.
(  0) 0) |
| [7] |
TANG D, QIN B, LIU T, et al. Learning sentence representation for emotion classification on microblogs[C]//Proceedings of Natural Language Processing and Chinese Computing. Berlin, 2013:212-223.
(  0) 0) |
| [8] |
SANTOS C N D, ZADROZNY B. Learning character-level representations for part-of-speech tagging[C]//Proceedings of the 31st International Conference on Machine Learning. New York, 2014:1818-1826.
(  0) 0) |
| [9] |
ZHANG X, ZHAO J, LECUN Y. Character-level convolutional networks for text classification[C]//Proceedings of the Advances in Neural Information Processing Systems. Montreal,2015:649-657.
(  0) 0) |
| [10] |
CHEN X X, XU L, LIU Z Y,et al. Joint learning of character and word embeddings[C]//Proceedings of International Joint Conference on Artificial Intelligence. San Francisco, 2015:1236-1242.
(  0) 0) |
| [11] |
MIKOLOV T, CHEN K, CORRADO G, et al. Efficient estimation of word representations in vector space[J]. Computer science, 2013, 1-12. (  0) 0) |
| [12] |
MIKOLOV T, SUTSKEVER I, CHEN K, et al. Distributed representations of words and phrases and their compositionality[C]//Proceedings of the Advances in Neural Information Processing Systems. South Lake Tahoe,2013:3111-3119.
(  0) 0) |
| [13] |
JIAN L, YANG L, SUGE W. The constitution of a fine-grained opinion annotated corpus on Weibo[C]//15th China National Conference on Computational Linguistics.Yantai, 2016:227-240.
(  0) 0) |
 2017, Vol. 49
2017, Vol. 49


