0 引言

经典的基于区域的主动轮廓模型是Chan等^[1]提出的C-V模型，应用于目标与背景灰度之间差别比较大的图像分割中.但对目标与背景灰度差别较小或存在灰度重叠的图像，通常会造成错分割.针对如何更灵活地运用区域信息来区分目标与背景，文献[2-4]提出了一系列改进的C-V模型.改进的C-V模型系列算法虽然充分考虑了全局信息，其初始曲线位置可以任意放置，但该模型对每个被分割区域内的灰度分布均匀性有严格要求.然而，在现实生活中，不同形式的图片灰度通常是不均匀的.特别是对于医学图像，其背景复杂，不同组织结构间的重叠以及成像时不可避免的噪声等，都会使图像存在灰度不均的问题.文献[5]提出了一种基于可伸缩区域拟合能量(region-scalable fitting，RSF)模型，该模型引入了一个以高斯函数^[6]为核函数的局部二值拟合能量，通过两个拟合函数分别逼近局部边界内部和外部的灰度，有效解决了灰度不均的问题.但是此类主动轮廓曲线演化到物体的某些弱边缘部分或者边缘间隙处，且灰度值又相近时，常常会发生泄露或者过分割.出现这个问题的原因，是由于模型并没有提供任何信息把这些断开的边缘间隙连接起来，而且模型分割速度相对较慢.文献[7]将基于全局信息的C-V模型与RSF模型结合，提出了LGIF(local and global intensity fitting)模型.相比传统RSF模型，LGIF模型虽然分割精度得到了提升，但是它的能量泛函比传统RSF模型复杂得多，所以分割速度较慢.文献[8]提出全局和局部拟合的活动轮廓模型，在C-V模型的水平集演化偏微分方程中加入RSF模型，使得最终的演化方程比LGIF模型简单，但是它依然比传统RSF模型的演化方程复杂，而且模型并没有采取任何措施提高分割速度，所以其分割速度仍然不容乐观.

为了提高模型的分割速度，有学者从能量泛函的最小化方式入手或通过选择不同的罚函数项来实现，文献[9]从核函数入手，通过改变核函数的几何特性实现分割性能的提升.因此，综合考虑模型的分割精度和速度两方面，本文提出了一种改进的RSF(modified region-scalable fitting，MRSF)模型.在使用RSF模型分割之前先对图像进行全局的K均值处理^[10]，实现在不改变能量泛函复杂度的情况下分割精度的提高；在传统RSF模型中用一个新的核函数代替高斯函数，实现了分割速度的提升；将一个内部能量项作为罚函数项引入到水平集模型中.将该方法应用在脑部医学方面，有效提高了图像分割的精度和速度.

1 RSF模型

基于自适应局部区域灰度拟合的主动轮廓模型，即RSF模型，该拟合模型的能量泛函定义为

$ \varepsilon _x^{{\rm{Fit}}}\left( {C,{f_1}\left( x \right),{f_2}\left( x \right)} \right) = \sum\limits_{i = 1}^2 {{\lambda _i}\int_{{\mathit{\Omega }_i}} {{K_\delta }\left( {x - y} \right){{\left| {I\left( y \right) - {f_i}\left( x \right)} \right|}^2}{\rm{d}}y} } , $

(1)

式中：λ₁, λ₂>0；f₁(x)和f₂(x)分别为逼近以x为中心的区域Ω₁和Ω₂的平均灰度值；I(y)是区域内任意一点y的灰度；Ω₁和Ω₂的范围由核函数K_δ控制，参数δ的值越大，区域范围就越大.核函数定义为高斯函数,

$ {K_\delta }\left( u \right) = \left[ {\frac{1}{{{{\left( {2{\rm{ \mathsf{ π} }}} \right)}^{\frac{n}{2}}}}}{\delta ^n}} \right]{{\rm{e}}^{ - \frac{{{{\left| u \right|}^2}}}{{2{\delta ^2}}}}}. $

(2)

可以看出，K满足局部性质：非负单减，而且$\mathop {\lim }\limits_{\left| u \right| \to \infty } K(u) = 0$.正是因为核函数具有局部性质，所以才使得f₁(x)和f₂(x)主要由x附近的灰度值决定.在RSF模型中，选取合适的核函数是至关重要的.

为了平滑边界曲线C，将边界的弧长|C|加入拟合函数中，总的能量泛函表示为水平集能量泛函,

$ \begin{array}{l} E\left( {\varphi ,{f_1}\left( x \right),{f_2}\left( x \right)} \right) = \sum\limits_{i = 1}^2 {{\lambda _i}\int {\left( {\int {{K_\delta }\left( {x - y} \right){{\left| {I\left( y \right) - {f_i}\left( x \right)} \right|}^2}{M_i}\left( {\varphi \left( y \right)} \right){\rm{d}}y} } \right){\rm{d}}x} } + \\ \nu \int {\left| {\nabla H\left( {\varphi \left( x \right)} \right)} \right|{\rm{d}}x} . \end{array} $

(3)

在f₁(x)和f₂(x)固定的条件下，相对于$\varphi $最小化式(3)，可得

$ \frac{{\partial \varphi }}{{\partial t}} = - \delta \left( \varphi \right)\left( {{\lambda _1}{e_1} - {\lambda _2}{e_2}} \right) + \nu \delta \left( \varphi \right){\rm{div}}\frac{{\nabla \varphi }}{{\left| {\nabla \varphi } \right|}}, $

(4)

其中:${e_i}(x) = {\int {{K_\delta }(y - x)\left| {I(x) - {f_i}(y)} \right|} ^2}{\rm{d}}y;{M_1}(\varphi (y)) = H(\varphi );{M_2}(\varphi (y)) = 1 - H(\varphi )$; H是Heaviside函数; ${H_\varepsilon }(z) = 0.5[1 + (\frac{2}{{\rm{ \mathsf{ π} }}}\arctan (\frac{z}{\varepsilon }))];\delta (x) = H(x);{\delta _\varepsilon }(z) = \frac{2}{{\rm{ \mathsf{ π} }}}(\frac{\varepsilon }{{{\varepsilon ^2} + {z^2}}})$.

在水平集演化方程(4) 中，e₁(x)、e₂(x)显然是水平集演化速度${\varphi _i}$极其重要的组成部分，是由核函数K(u)确定的.因此，选择合适的核函数K(u)是减少演化时间的有效措施.此外，RSF模型是基于梯度信息的主动轮廓模型，外力是基于图像的梯度信息，没有利用全局信息，所以对于某些医学图像的分割有时会出现欠分割、误分割等问题.

2 改进的RSF模型

针对RSF模型在分割精度与分割速度两方面存在的不足，提出了改进的RSF算法(MRSF).MRSF算法的思想为：① 利用K均值算法对原始图像做全局处理.② 选择合适的核函数替代高斯函数.③ 在新的核函数基础上，重新建立能量泛函，并将一个内部能量项作为罚函数项引入到水平集模型中.④ 在新的能量泛函的作用下对图像进行处理，得到最终的分割结果.

K均值聚类是最著名的划分聚类算法，同时也是一种最简单的聚类算法.在利用RSF模型对医学图像分割之前，先用K均值算法进行处理，相当于在算法一开始就先考虑了全局信息，这就在一定程度上解决了RSF模型没有利用全局信息的缺陷，从而提高了分割精度.由于K均值算法的本质是一个迭代过程，所以在RSF模型之前加入K均值预处理必然会存在时间方面的额外开销.但是，选择合适的核函数可以减少演化时间.

2.1 核函数

在选择不同于高斯函数的核函数之前，首先了解高斯函数的一些特征.由高斯函数的表达式(式(2))，可以得知其具有以下几个比较显著的几何特征：

1) 单调减少并且$\mathop {\lim }\limits_{\left| u \right| \to \infty } K(u) = 0$.

2) 存在拐点u=δ，因为高斯函数的二阶导数在u=δ处变号.

3) 随着|u|的增加，K_δ(u)迅速下降，并且$\mathop {\lim }\limits_{\left| {u \ge 3\delta } \right|} K(u) = 0$.

第1个特征是核函数必须满足的，但是后两个特征是不必要的, 第2个特征(存在拐点)导致了与中心点相距为δ的点与其他点处理的方式不同，第3个特征导致把与中心点相距超过3δ的点全部被忽略，这些特征对于核函数来说是不需要的.高斯函数的后两个特征使函数表达式、计算过程以及演化过程都过于复杂，影响了计算速度和曲线的收敛速度，导致演化速度变慢.为了简化核函数表达式以及避免高斯函数后两个特征的出现，选择如下函数作为核函数：

$ {K_q}\left( u \right) = \frac{1}{{1 + {u^q}}},q \in \left( {0,1} \right],u \ge 0. $

(5)

对于二维的情况，式(5) 中u的表达式为

$ u = x * q + y * q. $

(6)

在该核函数中之所以要求q∈(0, 1]，是因为q>1时，K_q(u)存在拐点，这就使得其与高斯函数的特征相似，影响了演化速度.

2.2 新的水平集能量泛函

将新的核函数(5) 带入式(3)，得到新的水平集能量泛函为

$ \begin{array}{l} E\left( {\varphi ,{f_1}\left( x \right),{f_2}\left( x \right)} \right) = \sum\limits_{i = 1}^2 {{\lambda _i}\int {\left( {\int {{K_q}\left( {x - y} \right){{\left| {I\left( y \right) - {f_i}\left( x \right)} \right|}^2}{M_i}\left( {\varphi \left( y \right)} \right){\rm{d}}y} } \right){\rm{d}}x} } + \\ \nu \int {\left| {\nabla H\left( {\varphi \left( x \right)} \right)} \right|{\rm{d}}x} . \end{array} $

(7)

为了使曲线在演化过程中始终保持零水平集函数，避免在演化的过程中重复初始化，定义一个内部能量项，并将它作为罚函数项引入到水平集模型中.罚函数的具体表达式为

$ p\left( \varphi \right) = \iint_{{\mathit{\Omega }_i}} {\frac{1}{2}{{\left( {\nabla \varphi - 1} \right)}^2}{\rm{d}}x{\rm{d}}y}. $

(8)

对t求偏导得

$ \frac{{\partial p}}{{\partial t}} = \nabla \varphi - {\rm{div}}\frac{{\nabla \varphi }}{{\left| {\nabla \varphi } \right|}} = {\rm{div}}\left[ {\left( {1 - \frac{1}{{\left| {\nabla \varphi } \right|}}} \right)\left| {\nabla \varphi } \right|} \right]. $

(9)

加入罚函数之后，总的能量泛函可以表示为

$ \begin{gathered} {E_{{\rm{MRSF}}}}\left( {\varphi ,{f_1}\left( x \right),{f_2}\left( x \right)} \right) =\\ \sum\limits_{i = 1}^2 {{\lambda _i}\int {\left( {\int {{K_q}\left( {x - y} \right){{\left| {I\left( y \right) - {f_i}\left( x \right)} \right|}^2}{M_i}\left( {\varphi \left( y \right)} \right){\rm{d}}y} } \right){\rm{d}}x} } + \hfill \\ \nu \int {\left| {\nabla H\left( {\varphi \left( x \right)} \right)} \right|{\rm{d}}x} + \gamma \iint_{{\mathit{\Omega }_i}} {\frac{1}{2}{{\left( {\nabla \varphi - 1} \right)}^2}{\rm{d}}x{\rm{d}}y}. \hfill \\ \end{gathered} $

(10)

在函数$\varphi $固定的条件下，相对f₁(x)和f₂(x)最小化式(10)，可得

$ {f_i}\left( x \right) = \frac{{{K_q}\left( x \right) * \left[ {{M_i}\left( {\varphi \left( x \right)} \right)I\left( x \right)} \right]}}{{{K_q}\left( x \right) * {M_i}\left( {\varphi \left( x \right)} \right)}},i = 1,2. $

(11)

在f₁(x)和f₂(x)固定的条件下，相对于$\varphi $最小化式(10)，可得

$ \frac{{\partial \varphi }}{{\partial t}} = - H\left( \varphi \right)\left( {{\lambda _1}{e_1} - {\lambda _2}{e_2}} \right) + \nu H\left( \varphi \right){\rm{div}}\frac{{\nabla \varphi }}{{\left| {\nabla \varphi } \right|}} + \gamma \left( {\nabla \varphi - {\rm{div}}\frac{{\nabla \varphi }}{{\left| {\nabla \varphi } \right|}}} \right). $

(12)

其中:${e_i}(x) = \int {{K_q}} (y - x){\left| {I(x) - {f_i}(y)} \right|^2}{\rm{d}}y;{M_1}(\varphi (y)) = H(\varphi );{M_2}(\varphi (y)) = 1 - H(\varphi )$; H是Heaviside函数; ${H_\varepsilon }(z) = 0.5[1 + (\frac{2}{{\rm{ \mathsf{ π} }}}\arctan (\frac{z}{\varepsilon }))]$.

在水平集演化方程(12) 中，e₁(x)、e₂(x)是水平集演化速度${\varphi _i}$最重要的组成部分，由式(2) 和(5) 可知，高斯函数无论在函数表达式还是在计算过程上都过于复杂；再加上高斯函数后两个几何特性，抑制了曲线收敛，这些因素最终导致了曲线演化速度变慢.

3 实验结果与分析

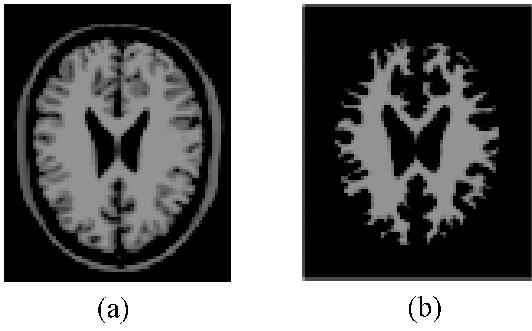
实验数据来源于全球著名医学资源网站BrainWeb中的脑部仿真MRI图像.实验环境为：联想台式计算机，64位MatlabR2012b.选取典型的脑部仿真MRI图像(图 1(a))，包括白质、灰质和脑脊液.把白质作为目标图像，其他部分都作为背景图像进行处理，图 1(b)是黄金分割标准下的白质部分.

3.1 图像全局处理对RSF模型的影响

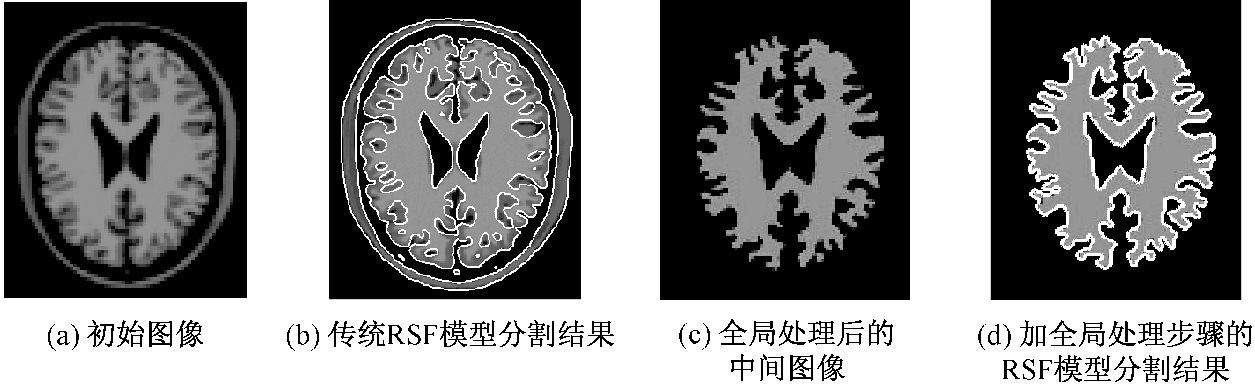
这部分实验主要验证加全局处理步骤的RSF模型，相比于传统RSF模型在分割精度方面的优越性.选取参数λ₁=λ₂=1.0，ν=0.001*255*255，Δt=0.1，μ=1，ε=1.0，δ=7.0，分割结果如图 2所示.可以看出，传统RSF模型在分割类似图 2(a)的MRI图像时，对于白质的分割精度是远远不够的(图 2(b))，这是因为在利用RSF模型分割之前没有提供关于图像的任何信息，而RSF模型本身又是基于图像的梯度信息；加全局处理步骤的RSF模型是先对MRI图像做K均值处理得到中间图像(图 2(c))，然后再对中间图像利用RSF模型进行分割，这就在分割之前一定程度上加入了人工干预和图像的全局信息，所以从图 2(d)可以看出，相比于传统RSF模型，其分割精度大大提升.

3.2 改进核函数对RSF模型的影响

这部分实验主要验证改进核函数的RSF模型，相比于传统RSF模型在分割速度方面的优越性.传统RSF模型的参数选取同3.1部分；改进核函数的RSF模型参数选取与传统RSF模型共有的参数(λ₁, λ₂, ν, μ等)保持一致，q=0.5.

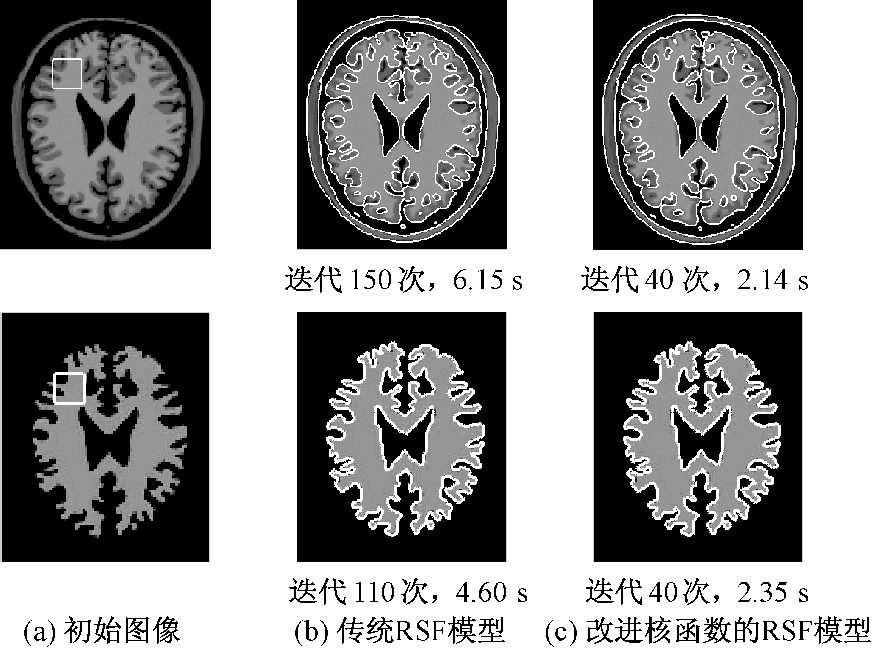
取得相似分割结果的分割时间对比如图 3所示.可以看出，在分割相同的图像并且取得相似分割结果时，改进核函数的RSF模型所用的分割时间远远小于传统RSF模型.但是MRSF模型在使用改进核函数的RSF模型之前进行了K均值全局处理，这个过程也必然会有时间的损耗.因此，将对MRSF模型与传统RSF模型在分割精度和分割速度方面进行比较.

3.3 综合比较实验

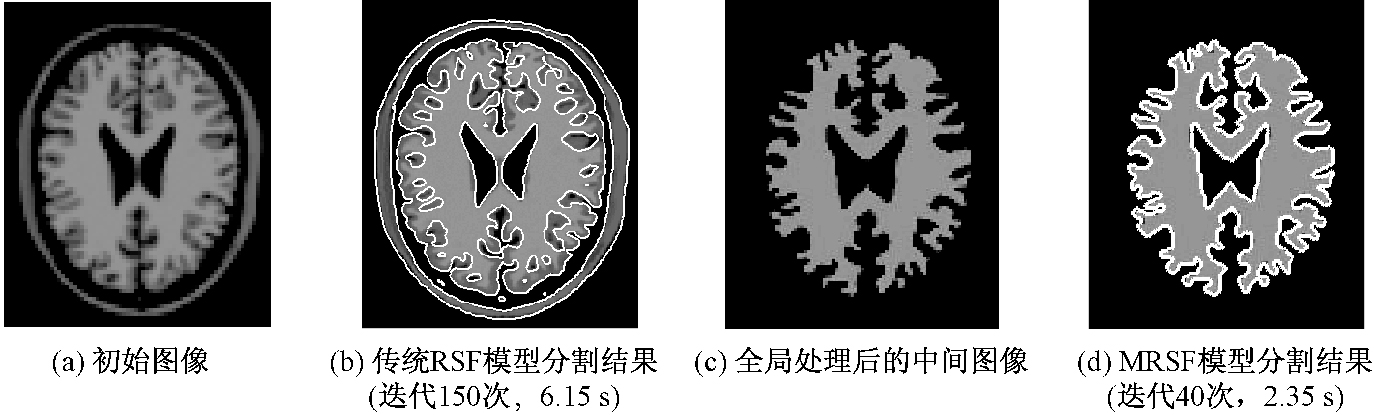
传统RSF模型的参数选取同3.1部分；MRSF模型的参数选取与传统RSF模型共有的参数(λ₁, λ₂, ν, μ等)保持一致，q=0.5，分割结果对比如图 4所示.

从图 4可以看出，本文模型无论在分割精度还是分割速度上都优于原模型.为了进一步定量评价MRSF模型的优越性，采用Jaccard系数和Dice系数两个相似性度量^[11]对图像分割结果进行评估.这两个指标越接近1，说明图像分割的结果越接近分割的黄金标准，算法的分割性能就越好.表 1和表 2分别为算法分割质量和分割时间评估结果.

由表 1可以清晰地看出，MRSF算法Jaccard系数和Dice系数都比传统RSF算法大，因此，本文算法分割精度更高，比传统RSF模型分割精度提升了近40%；由表 2可知，本文算法分割时间由原来的6.15 s减少到4.35 s，分割速度提升了近30%.

4 小结

本文提出的MRSF模型主要对传统RSF模型在分割精度和分割速度两方面进行了改进.在进行图像分割之前加入K均值步骤作全局处理，这就在分割之前一定程度上加入了人工干预和图像的全局信息，从而使得分割精度提升近40%.通过选择合适的核函数，使得分割速度提升近30%.实验结果表明，MRSF算法能够很好地分割灰度不均匀图像，并且分割速度也十分可观.但是由于K均值算法人工设定聚类数目的限制，该模型不具有普遍性，不能分割所有的图像.未来的研究就是要对模型进行优化，使其具有更广泛的适用范围，且更加智能化.