0 引言

股票市场受到多种因素的影响^[1]，特别是各种突发信息，使得股市波动具有高频性和多变性^[2]，这也使股市态势预测成为机器学习和数据挖掘领域的一个公开挑战.

一些研究者利用股市已出现的特征预测股市未来的态势^[3].郑献卫等提出了一种金融时序预测的特征预测模型^[4].马军海等讨论了一种非线性自相关混沌模型^[5]，选取了开盘价、收盘价、最高价、最低价等价格特征组合，但是仅提取股票一种或者一类指标，指标过于单一，无法充分获取当前股票信息.蔡红等将主成分分析方法与神经网络相结合研究股票较长波段^[6]，预测效果得到了提升, 但由于预测模型仅选取价格与成交量等简单指标，难以体现特征影响在时间上的传递性.

同时，一些学者从股票波动的角度进行研究.通过融合特征与时序参数，能够较有效地预测股市未来的态势，其中艾略特波浪理论是一种基于周期性思想的股市形态波动理论.李卫华将量价关系引入到艾略特波浪理论中，给出一种结合股市形态与成交量的相对关系的态势预测算法^[7].陈东峰等将波浪理论与时序自回归的ARMA模型(ARIMA)相结合进行态势预测^[8].这些波动算法较好地体现了特征演化性，但特征之间结构性不强，波段整体信息的融合度不高.

股票的波动存在滞后性特点^[9]，但是由于股票本身技术指标计算的周期不同，以及股票指标对波动性的敏感性不同，导致指标之间也存在着不一致的现象^[10].张润梅等在基于能量计算模型的贝叶斯网络股市态势预测算法^[11]中通过引入不一致特性的滞后性因素，提升了股票态势预测的效果.

从股市波动性的角度出发，通过对均线滞后性的融合，提出均线滞后的时序自回归股市态势预测算法(DSMA).首先，根据波浪理论定义股市中的W形态，根据Morse提出的信息不对称假说^[12]以及Stickel等关于量价关系的研究^[13]，结合形态相关指标，实现形态结点的量化.根据均线与形态指标的关系，计算均线滞后程度，并且构建均线滞后程度到结点的贝叶斯网络^[14-15]，根据网络中结点的结构关系，完成结点对均线滞后程度的融合; 进而，将W形态结点结构关系以及股票收盘价引入到AR模型中，构建预测模型.最后在实际数据上做了分析比较.

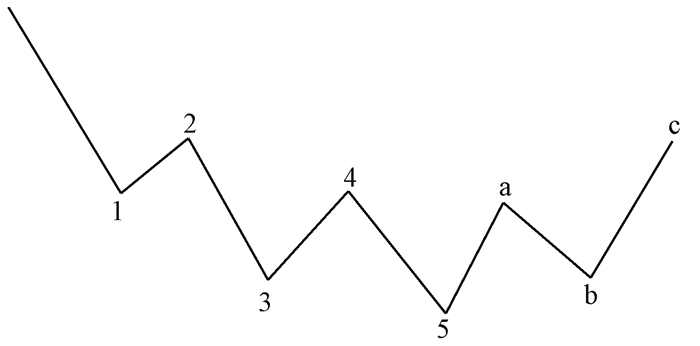
1 W形态结构建模 1.1 波浪理论

艾略特波浪理论是研究股市波动特性的一种重要模型.艾略特波浪理论从股市价格波动出发，将股市波动按照形态的上升、下降、调整分成8浪，如图 1所示，由5个下跌浪(1、2、3、4、5)和3个上升浪(a、b、c)组成.

1.2 股市中的W形态

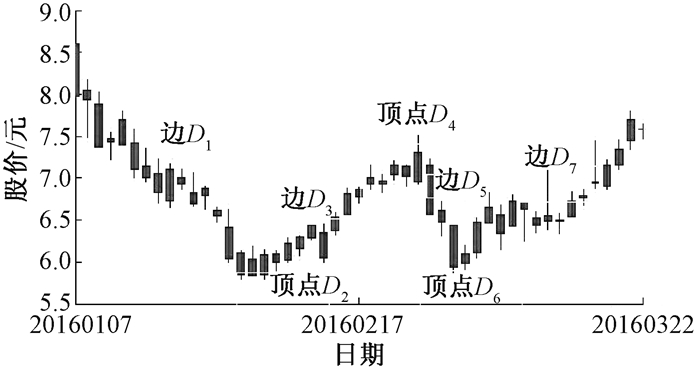
艾略特波浪理论是股市波动性的一种直观体现，而W形态是波浪理论中最复杂的部分，即图 1中的浪5到浪c.图 2的W形态由边D₁、D₃、D₅、D₇和顶点D₂、D₄、D₆组成.

W形态的确立是根据形态上涨边、下跌边以及底部特征确立的.针对下跌边D₁的下降幅度要求大于20%，上涨边D₃的上升幅度应该大于10%，下跌边D₅的下降幅度大于10%，边D₇作为预测结点不计算，仅取上涨幅度作为预测目标结点.当W形态由下跌阶段中开始出现股价最低价两个交易日连续上涨，即为底部的确立.当W形态由连续的上涨过程开始出现股票最高价连续两个交易日下跌，即为顶部特征的确立.

1.3 W形态结点的描述

W形态是量价关系和股票现阶段趋势的一种表现形式.从量价关系以及形态趋势入手对W形态各结点进行量化表示.

根据图 2，可知W形态结点集合为D={D₁, D₂, …, D₆}，对应状态值序列可以表示为d={d₁, d₂, …, d₆}，其中D₇是需要预测的结点, 其状态值用d₇表示.W形态成交量序列为A={a₁, a₂, …, a_n}，边结点D_i的跌幅用Df_i表示，涨幅用Zf_i表示.W形态中结点的具体描述如下.

1) 下跌边结点D_i.下跌缩量的程度和持续下跌的天数体现下跌的充分性，量化表示d_i=Df_i/T_i+ω(D_i)，其中：ω(D_i)表示边持续缩量情况，$\omega ({D_i}) = \sum\limits_{j = 1}^{{T_i}} {({a_{j + 1}}/{a_j});{T_i}} $表示边持续的天数.

2) 上升边结点D_k.上涨放量的程度和持续上涨的天数体现上涨的充分性，量化表示d_k=Zf/T_k+σ(D_k)，其中：σ(D_k)表示边的持续放量情况，$\sigma ({D_k}) = \sum\limits_{j = 1}^{{T_k}} {_i} ({a_j}/{a_{j + 1}});{T_k} $表示边持续的天数.

3) 底部结点D₂.第1个底部结点D₂与第2个底部结点的位置关系体现了股价的趋势，D₂成交量的变化体现底部趋势风险的释放，那么D₂的量化表示d₂=V(D₄)/V(D₂)+Avg(D₂)/V(D₂)，其中：Avg(D₂)表示结点D₂局部平均成交量; V(D_s)表示第s个结点的成交量.

4) 顶部结点D₄.根据结点D₂的描述，结点D₄的量化表示d₄=V(D₄)/Avg(D₄)+V(D₆)/V(D₄)，其中：Avg(d₄)表示点d₄局部平均成交量.

5) 底部结点D₆.底部顶点D₆受到成交量及均线影响，D₆的量化表示$ {d_6} = Avg({D_6})/V({D_6}) + 1/\sum\limits_{j = 1}^7 {|M{a_{{\rm{avg}}}} - M{a_i}|} $，其中：Ma_i表示连续i天的收盘价均值，Ma_avg表示Ma₁₀、Ma₂₀、Ma₃₀的平均值.

2 W形态均线滞后性

W形态结点的描述是通过成交量、股价相关指标，以及移动平均线计算获得的，但是股市指标与形态趋势之间是存在滞后关系的.对于存在滞后关系的W形态，根据W形态结点描述的结果实现预测的效果较差.均线作为股市中趋势性比较强的技术指标，对于股票后期的发展趋势具有较大的参考价值，也是持股人容易关注的技术指标.即使W形态构建完成，但是若均线趋势没有表现出成功收复的现象，那么也是一种风险释放不充分的表现.

2.1 均线滞后性

在W形态由快速下跌逐渐触底开始在底部产生波动，并且随着波动时间的增长，形态逐渐开始转势向上.在整个过程中波动的股价对目标均线不断产生影响，修正均线趋势，使均线下跌的趋势减缓，最终走平倒转向上.

因为股市的波动性非常大，在W形态形成的过程中，均线趋势发展并不一定能成功转势，往往滞后于W形态的发展，即滞后于W形态各结点.

定义1  均线滞后.移动平均线能够量化股市趋势，在W形态出现第2个底部时，形态趋势即移动平均线斜率依然向下，称之为均线滞后.

定理1  在W形态处于第2个底部时，均线滞后现象出现(均线斜率小于一个负数)，股价后期涨幅为S_z，对应的均线斜率为K_z，无均线滞后现象时股价后期的涨幅为S_w, 对应的均线斜率为K_w.则有S_w>S_z (K_w>K_z).

证明  W形态在第2个底部时上涨动能为E，当前成交量为M，均线值为L, 股价为P; 最后一个上涨波段结束时均线值为L′, 股价为P′.则股价涨幅可表示为S=(P′-P)/P，均线斜率表示为K=(L′-L)/L.

1) 当P>L时，均线作为股价的支撑线存在，股价以均线作为参考系向上增长, 与参考系距离变大，直至W形态动能转化殆尽为止，此时股价相对于均线上升幅度为(P′-L′)-(P-L)，有

$ \begin{array}{l} \left( {\left( {P\prime - L\prime } \right) - \left( {P - L} \right)} \right)\cdot M = E \Rightarrow \left( {P\prime - P} \right) - \left( {L\prime - L} \right) = E/M \Rightarrow \\ P\prime - P = \left( {L\prime - L} \right) + E/M \Rightarrow P\prime = \left( {L\prime - L} \right) + E/M + P. \end{array} $

因为$S = \left( {P\prime - P} \right)/P, K = \left( {L\prime - L} \right)/L $，可知$S = \left( {K\cdot L + E/M} \right)/P $.因股价P>0, 所以当K_w>K_z时，有S_w>S_z.

2) 当P < L时，均线作为股价的压力线存在，股价以均线作为参考系向上增长, 与参考系距离变小，直至W形态动能转化殆尽为止，此时股价相对于均线上升幅度为$\left( {L - P} \right) - \left( {L\prime - P\prime } \right) $，有

$ \begin{array}{l} \left( {\left( {L - P} \right) - \left( {L' - P'} \right)} \right)\cdot M = E \Rightarrow \left( {P\prime - P} \right) - \left( {L\prime - L} \right) = E/M \Rightarrow \\ P\prime - P = \left( {L\prime - L} \right) + E/M \Rightarrow P\prime = \left( {L\prime - L} \right) + E/M + P. \end{array} $

因为$ S = \left( {P\prime - P} \right)/P, K = \left( {L\prime - L} \right)/L$，可知$S = \left( {K\cdot L + E/M} \right)/P $.因为股价P>0, 所以当K_w>K_z时，有S_w>S_z.

证毕.

2.2 均线滞后程度

从W形态的边以及顶点的角度对W形态做描述，W形态均线的滞后程度也需要从结点的角度进行计算.由均线滞后的定义可知，均线滞后是指W形态中的结点无法完成使均线方向走平或者转向向上的效果，所以均线滞后是在W形态特定的结点处均线斜率没有变小的趋势.因为W形态是按照边及顶点描述的，所以需要分别从边及顶点的角度对滞后性做计算，结点序列(d₁, d₂, d₃, d₄, d₅, d₆)对应的均线滞后表示为(h₁, h₂, h₃, h₄, h₅, h₆).

1) 均线相对于边的滞后程度

边结点对应的时间段内均线的方向下降的趋势减缓，均线斜率逐渐减小，时间段内均线斜率累积的值相对于结点描述之间的差值的绝对值为均线的滞后程度，$ {h_i} = |{d_i} - \sum\limits_{k = j}^{k = j + m} {({P_k} - {P_{k - 1}})/{P_{k - 1}}} |$，其中：d_i表示边的描述; j表示边的起始时间; j+m表示边的结束时间; P_k表示时间为k时的收盘价.

2) 均线相对于顶点的滞后程度

出现顶点的时候，选取顶点处均线的斜率与顶点描述差值的绝对值作为均线的滞后程度，

$ {h_i} = |{d_i} - ({P_k} - {P_{k - 1}})/{P_{k - 1}}|. $

3 DSMA股市态势预测算法

均线滞后性是对W形态趋势相较于移动平均线的量化，通过融合均线滞后性的结点构建预测模型，能够提交预测模型稳定性，提高预测精度.作为波动连续的W形态各均线滞后程度与结点描述之间是存在相互关系的，通过进一步对结构关系的考虑使预测精度得到提升.

3.1 融合均线滞后的W形态结构关系

均线滞后特征是针对W形态边以及顶点结点进行计算的，但是作为一个连续的波段形态，每一个结点受到的影响不仅限于其对应的均线滞后程度.W形态所有滞后性都有可能对当前结点产生影响.

鉴于网络结构简单，本文使用K2算法学习滞后程度序列(h₁, h₂, h₃, h₄, h₅, h₆)同相关结点d_i的贝叶斯网络，来确定各要素之间的关联程度.为了屏蔽不直接相关滞后特征的影响，从贝叶斯网络中提取结点d_i马尔可夫毯(马尔可夫毯是关于目标结点的一种局部结构).

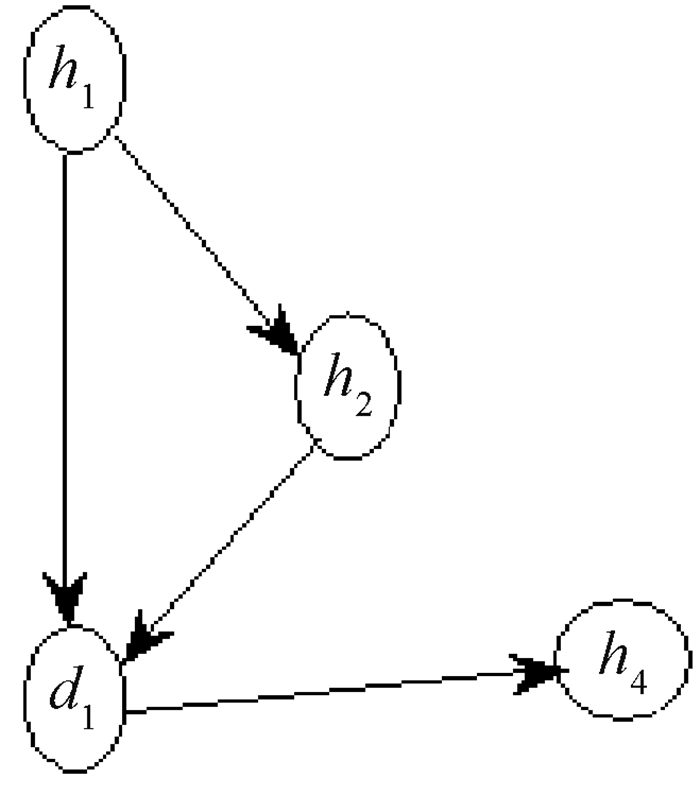
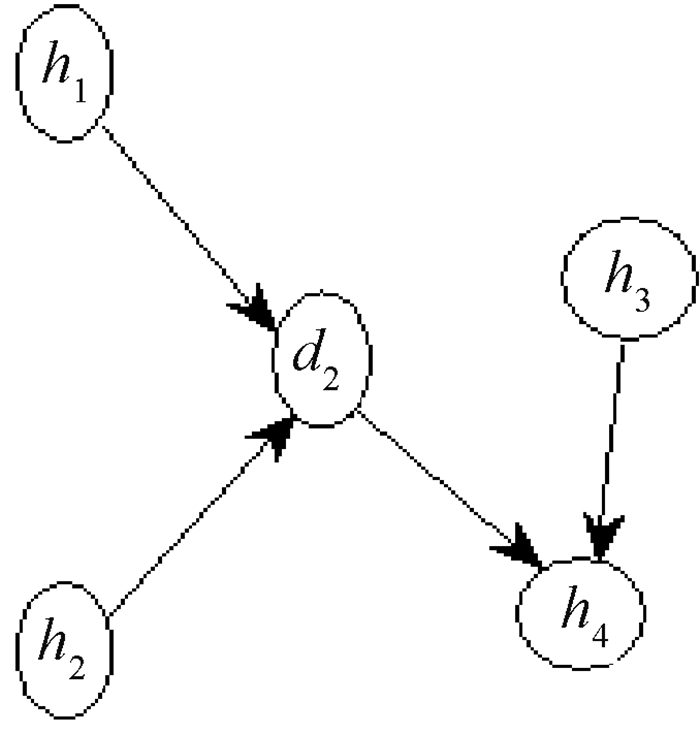
1) 结点的局部结构.图 3、图 4给出了结点d₁、d₂的马尔可夫毯，其他结点可以用同样方法进行计算.

使用非对称信息熵衡量均线滞后程度对结点的影响，其值的大小反映两个结点之间的影响程度.其计算方式^[16]为

$ {F_{xy}} = \sum\limits_Y ( - P({D_x} \to {D_y})*{\rm{log}}(P({D_x} \to {D_y})) - (1 - P({D_x} \to {D_y})) \\ *{\rm{log}}(1 - P({D_x} \to {D_y}))), $

(1)

其中：公式中的下标x、y为网络中的任意结点.

根据d₁、d₂的马尔可夫毯可以计算结点d₁、d₂融合均线滞后特征后的值r₁、r₂.

$ \begin{array}{l} {r_1} = {h_1}\cdot{F_{{h_1}}}_{{d_1}} + {h_2}\cdot{F_{{h_2}}}_{{d_1}} + {h_4}\cdot{F_{{h_4}}}_{{d_1}} + {d_1} = \left( {{h_1} \ldots {h_6}} \right)\cdot\left( {{F_{{h_1}}}_{{d_1}} \ldots {F_{{h_6}}}_{{d_1}}} \right) + {d_1}, \\ {r_2} = {h_1}\cdot{F_{{h_1}}}_{{d_2}} + {h_2}\cdot{F_{{h_2}}}_{{d_2}} + {h_3}\cdot{F_{{h_3}}}_{{d_2}} + {h_4}\cdot{F_{{h_4}}}_{{d_2}} + {d_2} = ({h_1} \ldots {h_6})\cdot({F_{{h_1}}}_{{d_2}} \ldots {F_{{h_6}}}_{{d_2}}) + {d_2}. \end{array} $

F_h1d1表示结点d₁马尔可夫毯中h₁到d₁的关系强度，如果结点的马尔可夫毯中h_i到d_i的边不存在，则F_hidi=0.其他结点(d₃, d₄, d₅, d₆)融合滞后特征的值(r₃, r₄, r₅, r₆)以同样方式计算.

2) 结点序列融合均线滞后. W形态结点序列(d₁，…，d₆)在融合均线滞后特征后用(r₁，…，r₆)表示，有

$ ({r_1}, {r_2}, {r_3}, {r_4}, {r_5}, {r_6}) = ({h_1} \ldots {h_6})\cdot\left( {\begin{array}{*{20}{c}} {{F_{{h_1}}}_{{d_1}}}& \ldots &{{F_{{h_1}}}_{{d_6}}}\\ \vdots &{}& \vdots \\ {{F_{{h_6}}}_{{d_1}}}& \ldots &{{F_{{h_6}}}_{{d_6}}} \end{array}} \right) + ({d_1} \ldots {d_6}) = \mathit{\boldsymbol{h\cdot F + d}}. $

(2)

3.2 目标结点预测模型

W形态最终结点D₇的上涨幅度受到融合滞后特征结点(r₁，…，r₆)的影响，利用AR模型对融合均线滞后特征的结点值(r₁，…，r₆)与目标结点d₇的关系进行建模.

1) AR模型.设{x_t}为零均值的平稳过程，则关于x_t的模型可表示为$ {x_t} = {\varphi _1}{x_{t - 1}} + {\varphi _2}{x_{t - 2}} + \ldots + {\varphi _p}{x_{t - p}} + {a_t}$，其中：a_t是白噪声序列; x_t遵循一个p阶自回归随机过程.

模型可表示为$ \mathit{\boldsymbol{Y = X \phi}} \mathit{\boldsymbol{ + a}}$，其中：

$ \mathit{\boldsymbol{Y}} = \left[ \begin{array}{l} {x_{n + 1}}\\ {x_{n + 2}}\\ \vdots \\ {x_N} \end{array} \right], \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{x_n}, }&{{x_{n - 1}}, }&{ \ldots , }&{{x_1}}\\ {{x_{n + 1}}, }&{{x_n}, }&{ \ldots , }&{{x_2}}\\ \vdots&\vdots &{}& \vdots \\ {{x_{N + n - 1}}, }&{{x_{N + n - 2}}, }&{ \ldots , }&{{x_N}} \end{array}} \right], \mathit{\boldsymbol{\phi}} = \left[ \begin{array}{l} {\varphi _1}\\ {\varphi _2}\\ \vdots \\ {\varphi _n} \end{array} \right]. $

2) W形态目标结点预测模型.利用AR模型对W形态融合滞后特征的结点序列(r₁，…，r₆)进行融合，得到W形态目标结点D₇的预测建模.由公式(2)得到h·F+d，作为AR模型的X，将结点D₇的涨幅d₇作为Y，则目标结点涨幅d₇的预测模型为

$ {\mathit{\boldsymbol{d}}_7} = \mathit{\boldsymbol{\phi}} \cdot\left( {\mathit{\boldsymbol{h\cdot F + d}}} \right) + \mathit{\boldsymbol{a}}, $

(3)

其中: $\mathit{\boldsymbol{Y}} = {\mathit{\boldsymbol{d}}_7};\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{h\cdot F}} + \mathit{\boldsymbol{d}} = ({h_1} \ldots {h_6})\cdot\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{{h_1}}}_{{d_1}}}& \ldots &{{\mathit{\boldsymbol{F}}_{{h_1}}}_{{d_6}}}\\ \vdots &{}& \vdots \\ {{\mathit{\boldsymbol{F}}_{{h_6}}}_{{d_1}}}& \ldots &{{\mathit{\boldsymbol{F}}_{{h_6}}}_{{d_6}}} \end{array}} \right) $ $+ ({d_1} \ldots {d_6});\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{{h_1}}}_{{d_1}}}& \ldots &{{\mathit{\boldsymbol{F}}_{{h_1}}}_{{d_6}}}\\ \vdots &{}& \vdots \\ {{\mathit{\boldsymbol{F}}_{{h_6}}}_{{d_1}}}& \ldots &{{\mathit{\boldsymbol{F}}_{{h_6}}}_{{d_6}}} \end{array}} \right) $ 表示W形态中均线滞后程度与结点之间的关系强度矩阵，即W形态的结构关系，由公式(1)可以获取.公式(3)的参数$ \mathit{\boldsymbol{\phi}} = {[{\varphi _1}, {\varphi _2}, \ldots , {\varphi _6}]^{\rm{T}}}$使用多维最小二乘法进行无偏参数估计，计算方式为

$ \mathit{\boldsymbol{\phi}} = {({\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}})^{ - 1}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{Y}} = {({\left( {\mathit{\boldsymbol{h\cdot F + d}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{h\cdot F + d}}} \right))^{ - 1}}{\left( {\mathit{\boldsymbol{h\cdot F + d}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{d}}_7}. $

(4)

3.3 DSMA预测算法

W形态均线滞后的时序预测算法(DSMA)具体描述如下.

输入：股市W形态前6个结点D₁、D₂、D₃、D₄、D₅、D₆阶段对应的开盘价、收盘价、最高价、最低价及5、10、20、30、60、120、250日移动平均线、成交量;

输出：W形态最后一个波段结束时的收盘价.

Step1：选取W形态案例，根据W形态各结点的计算方式，计算所有案例W形态各结点的描述值d_i.

Step2：根据均线滞后特征的计算公式计算各结点的均线滞后程度值h_i.

Step3：利用公式(1)计算均线滞后程度{h₁, h₂，…，h₆}与结点关系强度矩阵F.

Step4：将F、d_i、h_i代入到公式(3)中构建W形态结点D₇的预测模型.

Step5：通过公式(4)得到模型参数$\mathit{\boldsymbol{\phi}} $，完成预测模型的构建.

Step6：输入待预测案例成交量及股价序列，可以得到目标结点D₇的涨幅d₇的预测值，实现对股市的预测.

4 实验比对与分析 4.1 实验过程

针对日线级别的W形态和60分钟级别的W形态，取步长为3、5、10，分别在牛市、熊市以及震荡市展开实验，实验以PCA-BP^[5]算法作为对比实验，因为PCA-BP预测算法与本文预测算法都是以个股作为预测对象，两算法都是为了解决股市非线性问题.

以收盘价误差作为对算法预测精度的衡量标准，收盘价误差er的计算方式为

$ er = \left( {y - y\prime } \right)/y\prime $

(5)

其中：y表示收盘价的预测值; y′表示收盘价的真实值.其中的日线级别在牛市、震荡市、熊市阶段选取的训练集以及测试集如表 1所示.其中60分钟线级别在牛市、震荡市、熊市阶段选取的训练集以及测试集如表 2所示.均线滞后的时序预测算法DSMA和PCA-BP算法对于收盘价预测的平均误差如表 3所示.

均线滞后的时序预测算法DSMA和PCA-BP算法对于收盘价预测的平均误差如表 4所示，其中收盘价的预测误差的计算方式为公式(5).

由表 2与表 4可以看到，对于相同数据集，通过将各算法预测的收盘价与真实收盘价的对比发现，算法DSMA相对于算法PCA-BP的预测精度在熊市中效果最佳，震荡市次之，牛市预测效果相差不大，仅在60分钟级别步长为3的情况下效果略差于算法PCA-BP.实验结果表明均线滞后性的引入，提高了对熊市风险性的规避，提高了预测精度.结果进一步验证了均线滞后性是对股市风险的一种体现.

4.2 综合误差度量标准

用相对误差的平均值MAE评测算法精度，$ MAE = (\sum\limits_{i = 1}^n {|({y_i} - y\prime )/{y_i})|)/n} $，其中：y表示收盘价的预测值; y′表示收盘价的真实值; n表示选取的案例数目.相对误差的平均值MAE表示预测的总体效果，MAE值越小表示预测准确度越高.

4.3 综合误差

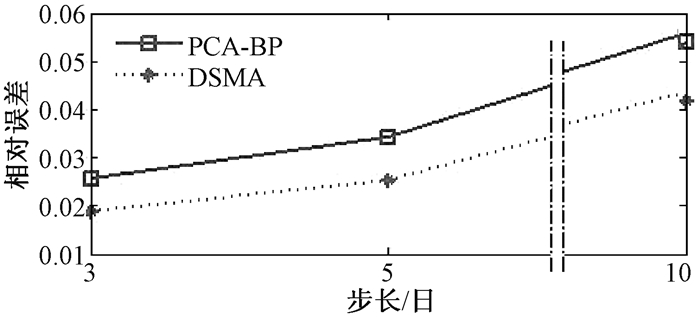
图 5给出了日线级别针对步长分别为3、5、10时平均误差MAE的折线图.

由图 5可知，在日线级别上算法DSMA针对不同步长的预测误差小于算法PCA-BP，随着预测步长的增加，算法DSMA预测精度变化的速度小于PCA-BP，结果显示出DSMA算法的优势.

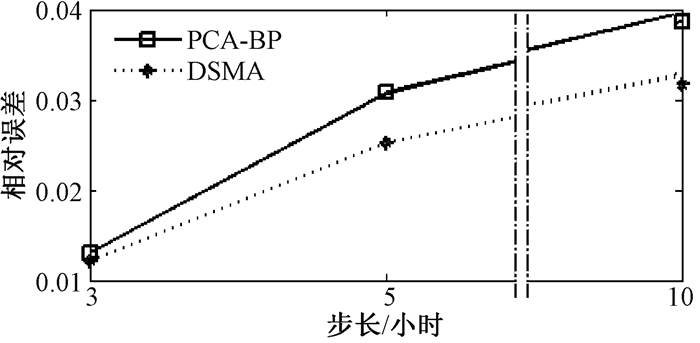
图 6给出了60分钟线级别，针对步长分别为3、5、10时平均误差MAE的折线图.

图 6可知，在60分钟线级别上，算法DSMA针对不同的步长的预测误差小于算法PCA-BP，随着预测步长的增加，算法DSMA预测精度变化的速度小于算法PCA-BP，这显示了算法DSMA的有效性.

5 结束语

针对波浪理论的局部结构提取W形态，从量价波动关系角度提取影响W形态走势的指标，对形态相关结点进行计算，根据结点均线滞后性特点对均线滞后性进行计算，利用贝叶斯网络生成W形态中均线滞后程度同结点的结构关系，根据结构关系、均线滞后程度、结点描述，对结点修正，进而通过AR模型对结合了滞后性的结点进行融合，从而完成均线滞后的股市态势预测算法DSMA.算法在不同周期以及不同市场环境下均取得比较好的效果，说明预测模型提出的必要性.为了进一步提升预测效果，后期还可以考虑市场情绪相关因素.