2. 西安石油大学 理学院 陕西 西安 710065
2. Department of Science, Xi′an Shiyou University Xi′an 710065, China
不确定性在现实世界中几乎无处不在,而模糊性是人们对一些概念无法给出清晰明确的界限而产生的不确定性[1]。由于无法对这些概念给出清晰的边界,它们的定量计算就会变得复杂。Zadeh[2]和Atanassov[3]最早提出了模糊集理论,将定性的信息定量化,来表达人们的定性决策信息,为模糊概念和模糊推理奠定了数学基础。由于数据信息模糊的原因,最终决策并不是完全精确的,但也加强了决策的可行性和可信性,为不同领域提供了一种新的思路。
模糊决策树具备传统决策树所有的优点,是数据挖掘中一种高效实用的方法。模糊决策树算法结构清晰,能从具有模糊条件属性和模糊决策属性的模糊决策表中归纳模糊决策树[4],适用于大规模数据学习问题,能够较好地处理数据中存在的不确定信息,并能生成可理解的模糊决策规则,以良好的计算速度运行。然而,在目前现实世界的诸多复杂场景中,数据的标签具有层次结构。如:在图书馆应用中,需要把图书文档信息组织成层次的主题;在网站页面管理中,海量的网页需要组织为层次目录的类别,方便用户快速检索。传统模糊决策树在处理标签具有层次结构的数据时有一定的不足。针对这类问题,本文提出一种可以从标签具有层次结构的数据中获取知识的层次模糊决策树。在此类数据中,底层的标签代表更加具体的概念,分类难度较大, 随着层次的提高,标签类别更加抽象,但是分类难度降低[5]。此时,如果单独使用层次结构的某一层标签分类,可能会导致分类准确率降低或损失相当一部分精度。这表明在构造算法过程中不能只考虑分类是否准确,还要在标签具体程度和分类准确率之间进行权衡。为了便于理解,预先定义标签的具体程度为标签的精度。本文提出的层次模糊决策树算法,在计算最优划分属性时,充分考虑了标签本身具有的层次结构,并在确定叶结点类别标签时,通过选择不同层次的分类标签来权衡分类的准确率和标签的精度。通过实验发现,与传统模糊决策树进行对比,本文提出的算法能做到在分类准确率尽可能高的情况下,同时层次标签尽可能具体。
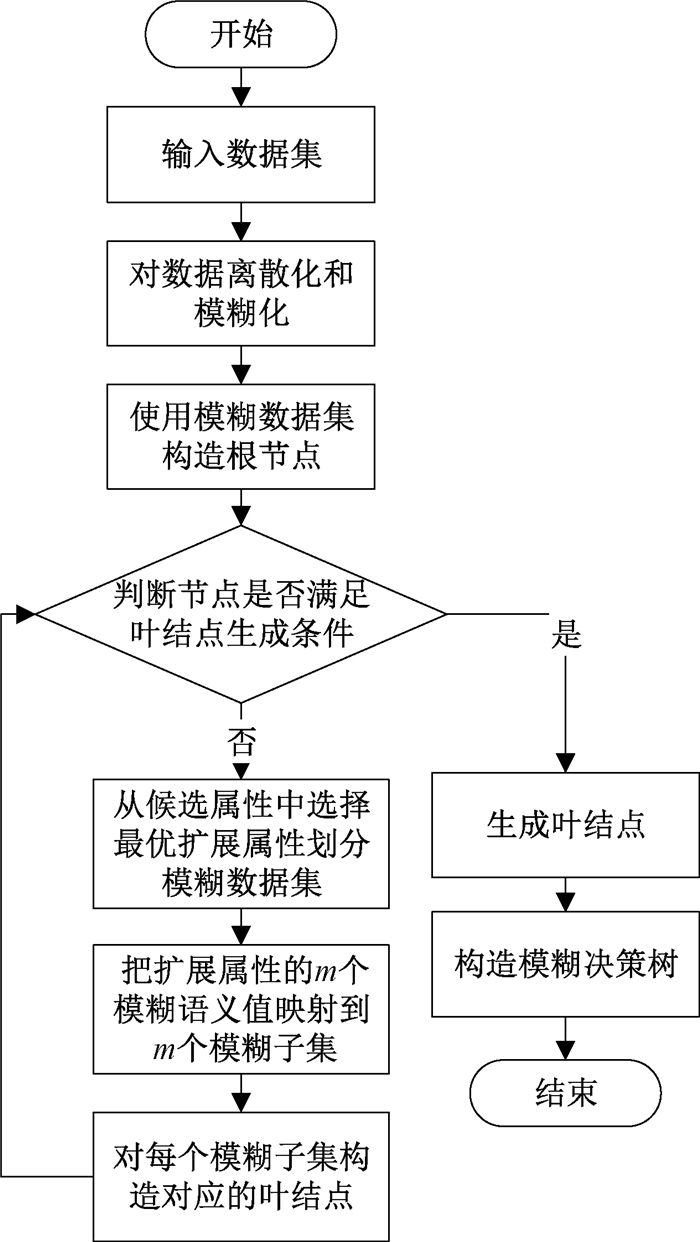
1 定义与问题描述 1.1 模糊决策树模糊决策树是对传统决策树的推广,同时具备决策树的算法思想和模糊集理论对处理不确定信息的优势。通常模糊决策树在处理属性是连续值的分类时,需要使用分割点对属性进行离散化和模糊化。模糊决策树可以按图 1流程构建。
|
图 1 模糊决策树构建流程 Fig. 1 Construction process of fuzzy decision tree |
定义1 模糊集[6]。设A是论域U到[0, 1]的一个映射,即A: U→[0, 1], u↦A(u) 称A为U上的模糊集,A(u)为模糊集A的隶属函数。
通常模糊集合可以使用Zadeh表示法:
| $ A=\{(u, A(u)) \mid u \in U\}。$ |
定义2 三角隶属函数[7]。三角隶属函数是一种分段函数,用于对数据进行模糊化处理,各个模糊语义值的隶属度函数如下:
| $ \mu_{T_{1}}(x)=\left\{\begin{array}{c} 1, & x \leqslant m_{1}, \\ \frac{m_{2}-x}{m_{2}-m_{1}}, & m_{1}<x<m_{2}, \\ 0, & x \geqslant m_{2}, \end{array}\right. $ |
| $ \mu_{T_{i}}(x)=\left\{\begin{array}{c} 0, & x \leqslant m_{i-1}, \\ \frac{x-m_{i-1}}{m_{i}-m_{i-1}}, & m_{i-1}<x \leqslant m_{i}, \\ \frac{m_{i+1}-x}{m_{i+1}-m_{i}}, & m_{i}<x \leqslant m_{i+1}, \\ 0, & x>m_{i+1}, \end{array} \ \ 1<i<k ,\right. $ |
| $ \mu_{T_{k}}(x)=\left\{\begin{array}{cc} 0, & x \leqslant m_{k-1}, \\ \frac{x-m_{k-1}}{m_{k}-m_{k-1}}, & m_{k-1}<x<m_{k}, \\ 1, & x \geqslant m_{k} 。\end{array}\right. $ |
定义3 对于一个模糊数据集D,dq为模糊类别,定义Ddq为D中类别为dq的模糊子集,1≤q≤Q,Q为模糊类别的数量。则模糊数据集D关于所有模糊类别的模糊熵定义为[8]
| $ { FEntr }^{D}=-\sum\limits_{q=1}^{Q} p_{q}^{D} \log _{2} p_{q}^{D}, $ | (1) |
其中:
定义4 假设模糊数据集D有n个条件属性,记A1, A2, …, An,1≤k≤n,其中条件属性Ak有Gk个模糊属性值,记为Tgk,1≤g≤Gk,故条件属性Ak能把D划分为Gk个模糊子集,记为DTgk。条件属性Ak相对于D的模糊熵定义为
| $ { FEntr }^{A^{k}, D}=\sum\limits_{g=1}^{G_{k}} \eta_{g}^{k} \cdot { FEntr }^{D^{T_{g}^{k}}}, $ | (2) |
其中:
定义5 条件属性Ak相对于D的模糊信息增益定义为
| $ G^{A^{k}, D}=F E n t r^{D}-F E n t r^{A^{k}, D}。$ | (3) |
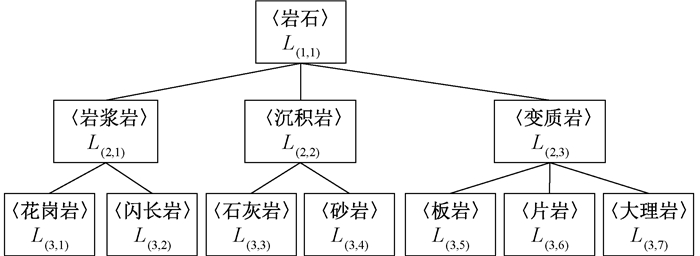
定义6 类别层次树(class hierarchical tree,CHT)是一种父标签节点的概念能覆盖其子标签节点概念的树状结构[9]。令CHT={L1, L2, …, Lh}, 其中: Li为CHT的第i层;h为CHT层数。L1是最抽象的一层,L2, L3,…, Lh所指代的标签逐渐具体,Li={Li, j |i=1, 2, …, h且j=1, 2, …, mi},Li,j指第i层的第j个类标签,mi表示第i层的类标签总数。
例如岩石分类,父标签〈岩石〉的概念将覆盖其子标签〈岩浆岩〉、〈沉积岩〉、〈变质岩〉,而〈沉积岩〉标签也会覆盖〈石灰岩〉、〈砂岩〉子标签,三层标签从上至下指代信息逐渐具体。岩石类层次树如图 2所示。
|
图 2 岩石类别层次树 Fig. 2 A class hierarchical tree of rock |
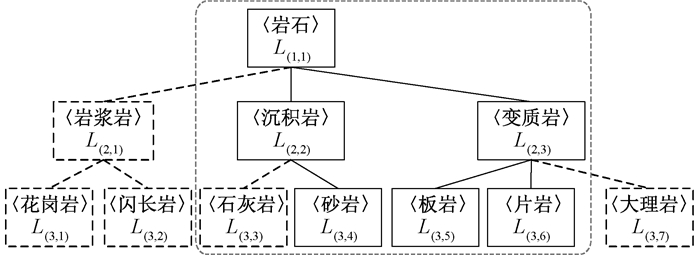
定义7 部分层次树(partial hierarchical tree,PHT)是CHT的最小子树,包含了某一个节点所有数据的标签[9]。
当某一节点数据不包含类别层次树全部标签时,就可使用PHT来代替CHT,用来减少计算复杂度。如某一节点v中只包含〈砂岩〉、〈板岩〉、〈片岩〉时,可以构建图 3的部分层次树。
|
图 3 岩石的部分类层次树 Fig. 3 A partial hierarchical tree of rock |
在模糊决策树算法中,模糊熵被用来判断当前节点在构建决策树时是否恰当,但是模糊熵并不能很好地在构建模糊决策树过程中处理标签具有层次结构的数据,下面用一个例子来说明。假设表 1和表 2分别为两个节点a和b的数据。表 1属性A包含a1、a2两个属性值;属性B包含b1、b2两个属性值,表中的数值是隶属度,代表属性取某一属性值的隶属程度。表 2同理,d1、d2、d3、d4代表决策属性,如d1代表〈石灰岩〉、d2代表〈砂岩〉、d3代表〈花岗岩〉、d4代表〈板岩〉。
|
|
表 1 节点a样例集 Tab. 1 A sample set of node a |
|
|
表 2 节点b样例集 Tab. 2 A sample set of node b |
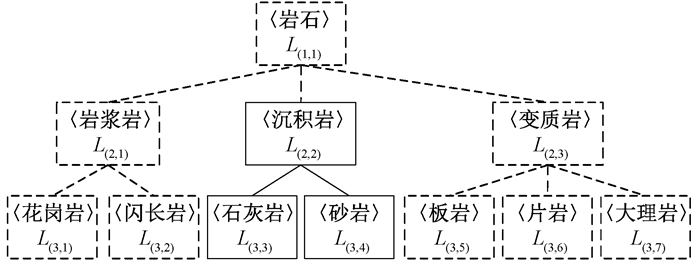
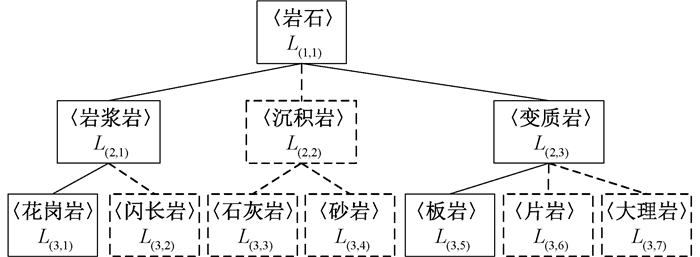
通过计算模糊熵发现,节点a和b的模糊熵都为1,而且无论给当前表中的数据分配哪个标签,节点a和b的分类准确率最高只能达到50%。这表明模糊熵度量方式无法判断两个节点谁更恰当。但如果把表中标签组织为标签树时,部分层次树见图 4、5,表 1决策属性d1、d2属于第二层标签〈沉积岩〉。表 2决策属性d3属于第二层标签〈岩浆岩〉,d4属于第二层标签〈变质岩〉,同时〈岩浆岩〉和〈变质岩〉属于第一层标签〈岩石〉。假设给节点a分配〈沉积岩〉标签,节点b分配〈岩石〉标签,此时两个节点准确率都达到100%,但节点a比节点b分配的标签更加具体。故在准确率相同的情况下,节点a的标签树的分布优于节点b,节点a更加适合节点划分。
|
图 4 节点a的部分类层次树 Fig. 4 A partial hierarchical tree of node a |
|
图 5 节点b的部分类层次树 Fig. 5 A partial hierarchical tree of node b |
上述例子说明,当标签分布是层次结构时,传统模糊熵不能很好地衡量节点适当性。
2 层次模糊决策树算法在模糊决策树算法设计中,属性选择有很多启发式方法,通过不同的启发式能计算出最能区分当前节点的属性。常用的启发式有三种:1) 模糊熵。模糊ID3算法使用模糊熵作为启发式。2) 最小分类不可指代性。Yuan等[10]提出的启发式使用最小分类不可指代性来选择扩展属性。3) 属性对于分类贡献重要度。Wang等[11]基于属性对于分类贡献重要度给出一种新的启发式来选择扩展属性。其中模糊ID3算法的计算复杂性最低,实际应用比较广泛,是学习精度较高的启发式。
标签具有层次结构时可知,属于某一个类别的样本,也自动的归属于它在CHT中的所有超类[12]。根据层次熵的思想[9],在选择最优扩展属性时,不仅要计算数据集关于底层标签的熵,还要计算数据集关于底层标签的所有超类的熵,最后根据权重求和得出数据集关于整个标签树的层次熵。
在构建模糊决策树模型之前,先要对数据表进行离散化和模糊化的预处理。对于数据表中的连续属性,采用Kohonen聚类算法[7]对其进行离散化,生成k个中心点,把属性划分为对应数量的模糊语义值,然后使用三角隶属函数,利用生成的模糊语义值完成对数据的模糊化,得到模糊数据集。
使用模糊ID3算法构建模糊决策树首先要计算模糊数据集关于所有模糊类别的模糊熵,其次计算属性Ak相对于数据集的模糊熵,最后可求得属性Ak的模糊信息增益。因此在计算具有层次标签的模糊数据集D关于所有模糊类别的模糊熵时,依据层次熵的思想,不仅要计算D关于底层模糊类别的模糊熵,还要计算D关于底层模糊类别的所有超类的模糊熵,然后通过CHT不同层次的权重ωi,得到D关于整个类层次树的模糊熵,称为层次模糊熵HFEntrD。按同样的思路可计算出属性Ak相对于D的层次模糊熵HFEntrAk, D,进而求得属性Ak相对于D的模糊信息增益,称为层次模糊信息增益HGAk, D。最终根节点选择max{HGAk, D},1≤k≤n。按上述思想构造的算法称为层次模糊决策树算法,用以解决具有层次标签数据的模糊决策树分类问题。算法遵循决策树归纳的标准框架[13],在层次模糊决策树构建好之后,可以把决策树抽象为多组模糊规则,从树的根节点到任意一个叶结点所形成的路径就构成一组模糊规则,模糊规则可定义为if条件then结论的形式[14]。上述算法所提概念计算步骤如下。
1) 模糊数据集D的层次模糊熵HFEntrD定义为
| $ H F E n t r^{D}=-\sum\limits_{i=1}^{h} \sum\limits_{j=1}^{m_{i}} \omega_{i}\left(p_{i, j}^{D} \log _{2} p_{i, j}^{D}\right), $ | (4) |
其中:ωi为CHT每一层的权重[9],
2) 属性Ak相对于D的层次模糊信息熵HFEntrAk, D定义为
| $ { HFEntr }{ }^{A^{k}, D}=\sum\limits_{g=1}^{G_{k}} \eta_{g}^{k} H F E n t r^{D^{T_{g}^{k}}}, $ | (5) |
其中:
3) 由步骤1)~2)计算出属性Ak的层次模糊信息增益HGAk,
| $ H G^{A^{k}}=H F E n t r^{D}-H F E n t r^{A^{k}, D} 。$ | (6) |
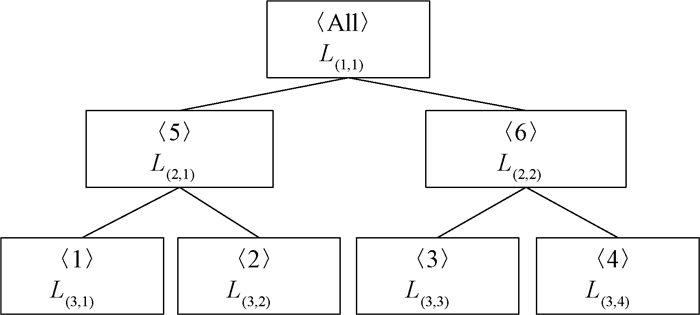
假设模糊数据集D,如表 3所示,给定类别层次树(CHT)如图 6所示。
|
|
表 3 模糊数据集D Tab. 3 A fuzzy data set D |
|
图 6 模糊数据集D的类别层次树 Fig. 6 The CHT of fuzzy data set D |
第一步:计算模糊数据集D的层次模糊熵。先要计算D关于CHT每一层标签的模糊熵,使用公式(1)计算可得如下结果。
第三层:
| $ \begin{aligned} &\ \ \ \ F E n t r_{h=3}^{D}=-\frac{2}{6} \log _{2} \frac{2}{6}-\frac{1}{6} \log _{2} \frac{1}{6}-\frac{2}{6} \log _{2} \frac{2}{6}-\\ &\frac{1}{6} \log _{2} \frac{1}{6}=1.918\ 3。\end{aligned} $ |
第二层:标签〈1〉、〈2〉属于第二层标签〈5〉;〈3〉、〈4〉属于标签〈6〉。
| $ F E n t r_{h=2}^{D}=-\frac{3}{6} \log _{2} \frac{3}{6}-\frac{3}{6} \log _{2} \frac{3}{6}=1.0 , $ |
| $ \omega_{1}=0, \omega_{2}=\frac{2(h-i+1)}{h(h-1)}=\frac{2(3-2+1)}{3(3-1)}=\frac{2}{3}, \omega_{3}=\frac{1}{3} 。$ |
由公式(4)可知模糊数据集D的层次模糊熵HFEntrD为
| $ 1.0 \times \frac{2}{3}+1.918\ 3 \times \frac{1}{3}+0=1.306\ 1 \text { 。} $ |
第二步:计算属性A相对于D的层次模糊信息熵HFEntrA, D。先用属性A的第一个属性值去划分D,得到一个模糊子集DT1A,在此模糊子集上,由公式(2)计算出DT1A在CHT每一层的模糊熵。
第三层:
| $ \begin{aligned} &{ FEntre }_{h=3}^{D{^{T_{1}^{A}}}}=-\frac{0.7+0.8}{0.7+0.6+0.4+0.8+0.3} \times \\ &\log _{2} \frac{0.7+0.8}{0.7+0.6+0.4+0.8+0.3}- \\ &\frac{0.6}{0.7+0.6+0.4+0.8+0.3} \times \\ &\log _{2} \frac{0.6}{0.7+0.6+0.4+0.8+0.3}- \\ &\frac{0.4+0.3}{0.7+0.6+0.4+0.8+0.3} \times \\ &\log _{2} \frac{0.4+0.3}{0.7+0.6+0.4+0.8+0.3}-0=1.458\ 6。\end{aligned} $ |
第二层:
| $ \begin{aligned} & { FEntro }_{h=2}^{D^{T_{1}^{A}}}=-\frac{0.7+0.8+0.6}{0.7+0.6+0.4+0.8+0.3} \times \\ &\log _{2} \frac{0.7+0.8+0.6}{0.7+0.6+0.4+0.8+0.3}- \\ &\frac{0.4+0.3}{0.7+0.6+0.4+0.8+0.3} \times \\ &\log _{2} \frac{0.4+0.3}{0.7+0.6+0.4+0.8+0.3}=0.811\ 3 。\end{aligned} $ |
按照权重计算:
| $ \begin{gathered} \eta_{1}^{A} { HFEntr }^{D^{T_{1}^{A}}}=\frac{0.7+0.6+0.4+0.8+0.3}{6} \times \\ \left(1.458\ 6 \times \frac{1}{3}+0.811\ 3 \times \frac{2}{3}\right)=0.479\ 3 。\end{gathered} $ |
同理可计算属性A的第二个属性值A2划分D时的模糊熵η2AHFEntrDT2A=0.632 9。按公式(5),属性A相对于D的层次模糊信息熵
| $ { HFEntr }^{A, D}=0.479\ 3+0.632\ 9=1.112\ 2。$ |
按公式(6)可计算属性A的层次模糊信息增益为
| $ \begin{aligned} &H G^{A}=H F E n t r^{D}-H F E n t r^{A, D}=1.306\ 1- \\ &1.112\ 2=0.193\ 9 。\end{aligned} $ |
使用以上公式便可求得HGB、HGC,选择层次模糊信息增益最大的属性作为根节点。
算法伪代码见算法1。
输入:模糊数据集。
① 初始化决策树T。
② 按照公式(4)~(6)确定根节点。
③ 按节点停止分配标准判断当前节点是否为叶结点。
if当前节点为叶结点
then给当前叶节点分配标签,标签分配要考虑CHT的层次结构。通过计算当前节点能分配给底层所有的模糊类别和这些类别所有超类的准确率为
else
选择层次模糊信息增益最大的节点作为扩展属性,并划分模糊数据集,产生子节点。
end if
④ 递归执行步骤③,得到一颗完整的层次模糊决策树。
输出:层次模糊决策树T。
其中|D(v, Li,j)|表示在节点v中标签是Li,j的样本数量。pre(Li,j)可表示为标签的精度,用于衡量标签的抽象程度。越接近底层,标签的精度越高,标签越具体。
节点停止分配标准为:1) 没有可用扩展属性。2) 当前节点某个分类的相对频率pi,j大于等于给定阈值β0。3) 节点样本数量为0或所有样本都属于同一类。
3 实验分析与评价 3.1 实验数据及预处理论文实验数据来源于UCI公开数据集Glass。此数据集包含214个样本,数据集有Mg、Ba、Ai、Fe、Ri、Na等9个属性,样本标签可以组织成一个4层的类别标签树; 第四层标签有〈1〉、〈2〉、〈3〉、〈4〉、〈5〉、〈6〉、〈7〉;第三层标签有〈FP〉(包括子标签〈1〉,〈3〉)、〈NFP〉(包括子标签〈2〉,〈4〉);第二层标签分布〈WG〉(包括子标签〈FP〉, 〈NFP〉)、NWG(包括子标签〈5〉,〈6〉,〈7〉);顶层为〈ALL〉。实验选取70%的数据作为训练集来构造层次模糊决策树,剩余30%的数据作为测试集用于验证结果。
对于数据集中的连续值属性,首先需要对数据离散化。实验使用Kohonen算法确定k个中心点,把属性划分为对应数量的模糊语义值。本实验将中心点k设置2,学习率设置为0.5。所求中心点部分计算结果如表 4所示。
|
|
表 4 数据中心点 Tab. 4 Center point of data |
由于中心点参数k设置2,每个属性会离散化为两个模糊语义值,为了表述方便,这里把每个属性的模糊语义值统一抽象为more和less。用这两个模糊语义值就能描述连续值属性。然后使用定义2的三角模糊隶属函数对数据集进行模糊化处理。模糊化后的部分数据如表 5。
|
|
表 5 部分模糊数据集 Tab. 5 Part of fuzzy data set |
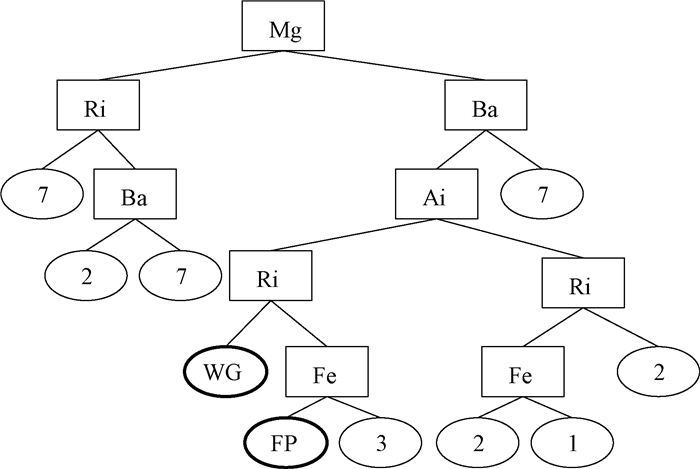
得到模糊数据集后,使用第三节提出的层次模糊决策树算法构建出决策树,并分配好类别标签,由于分配标签时,考虑了CHT的不同层次,所以生成的决策树中可以分配到除CHT底层标签外其他层次的标签。
如图 7所示,边框加粗的叶子标签即为CHT的上层标签,决策树左分支属性值为more,右分支属性值为less。
|
图 7 层次模糊决策树 Fig. 7 Hierarchical fuzzy decision tree |
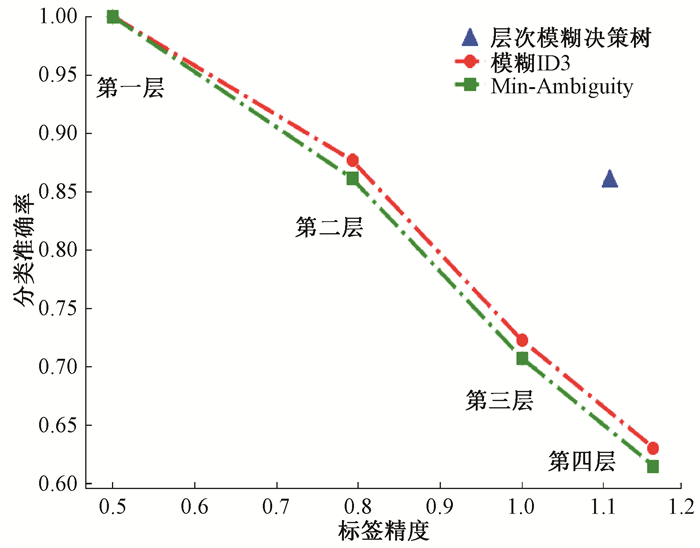
实验使用两个评价标准对模型性能进行评价:分类准确率和标签精度。标签精度数值越大说明样本所分配的层次标签越具体。为了更好地说明实验结果,使用模糊决策树中模糊ID3算法和基于最小分类不可指定性(Min-Ambiguity)算法为参照。由于传统模糊决策树(FDT)不能直接处理层次标签,需要分别把CHT每一层的标签当成模糊决策树的分类标签,然后去计算模糊决策树的标签精度和分类准确率,由于数据集的标签树有4层,使用模糊决策树算法就会有4个分类准确率数值和4个标签精度数值。而层次模糊决策树(HFDT)算法在构建决策树过程中就考虑了标签的层次结构,所以算法的标签精度和分类准确率是一个固定数值[5]。计算结果见表 6。
|
|
表 6 FDT和HFDT的分类准确率和标签精度 Tab. 6 Accuracy and label precision of FDT and HFDT |
从表 6和图 8可以看出,当所有数据都归于CHT第一层的单个标签时,传统模糊决策树的两个分类算法准确率最高,但是,标签精度最低,这样的分类并没有意义。当所有数据分别归于CHT的二、三、四层的标签时,标签精度逐渐提高,相应地,模糊ID3算法和Min-Ambiguity算法分类准确率也随之降低。其中模糊ID3算法在CHT除第一层外所有层次的分类准确率均优于Min-Ambiguity算法。这充分说明传统的模糊决策树分类器不擅长处理标签具有层次结构的数据,导致平衡标签精度和分类准确率的能力不佳, 也说明选取CHT其中一个层次的标签去分类数据并不合适,而层次模糊决策树模型在选择最优扩展属性时就考虑到了标签的层次结构, 从图 8折线图可以清晰看出,本文所提算法的标签精度和分类准确率与其他两个算法相比较,都保持在一个较高的数值,能做到在分类准确率尽可能高的情况下,同时层次标签尽可能具体。因此可以说明,本文提出的算法优于传统的模糊决策树算法。
|
图 8 FDT和HFDT折线对比图 Fig. 8 Line chart between FDT and HFDT |
模糊决策树是对传统清晰决策树在模糊理论上的扩展,具有决策树本身的优点,而且融合了模糊理论的优势。然而在处理标签具有层次结构的数据时,模糊决策树存在一定不足,本文提出的算法在构造过程中充分考虑到了标签的层次结构,使得分类准确率和标签精度都达到一个较高的水准,能有效处理这类问题,为决策者提供更加可信的信息。
| [1] |
廖虎昌, 缑迅杰, 徐泽水. 基于犹豫模糊语言集的决策理论与方法综述[J]. 系统工程理论与实践, 2017, 37(1): 35-48. LIAO H C, GOU X J, XU Z S. A survey of decision making theory and methodologies of hesitant fuzzy linguistic term set[J]. Systems engineering-theory & practice, 2017, 37(1): 35-48. (  0) 0) |
| [2] |
ZADEH L A. Fuzzy sets[M]. Singapore: World Scientific Press, 1996: 394-432.
(  0) 0) |
| [3] |
ATANOSSOV K. Intuitionistic fuzzy sets[J]. International journal bioautomation, 2016, 20(2): 107-115. (  0) 0) |
| [4] |
翟俊海, 侯少星, 王熙照. 粗糙模糊决策树归纳算法[J]. 南京大学学报(自然科学), 2016, 52(2): 306-312. ZHAI J H, HOU S X, WANG X Z. Induction of rough fuzzy decision tree[J]. Journal of Nanjing university (natural sciences), 2016, 52(2): 306-312. (  0) 0) |
| [5] |
HU H W, CHEN Y L, TANG K. A novel decision-tree method for structured continuous-label classification[J]. IEEE transactions on cybernetics, 2013, 43(6): 1734-1746. DOI:10.1109/TSMCB.2012.2229269 (  0) 0) |
| [6] |
李永明, 李平. 模糊计算理论[M]. 北京: 科学出版社, 2016. LI Y M, LI P. Fuzzy computing theory[M]. Beijing: Science Press, 2016. (  0) 0) |
| [7] |
王熙照, 谢凯. 基于聚类的数据预处理对模糊决策树产生的影响[J]. 计算机工程与应用, 2006, 42(1): 156-158, 186. WANG X Z, XIE K. Clustering-based data preprocessing's impact on fuzzy decision tree generation[J]. Computer engineering and applications, 2006, 42(1): 156-158, 186. (  0) 0) |
| [8] |
KHAZALI N, SHARIFI M, AHMADI M A. Application of fuzzy decision tree in EOR screening assessment[J]. Journal of petroleum science and engineering, 2019, 177: 167-180. DOI:10.1016/j.petrol.2019.02.001 (  0) 0) |
| [9] |
CHEN Y L, HU H W, TANG K. Constructing a decision tree from data with hierarchical class labels[J]. Expert systems with applications, 2009, 36(3): 4838-4847. DOI:10.1016/j.eswa.2008.05.044 (  0) 0) |
| [10] |
YUAN Y F, SHAW M J. Induction of fuzzy decision trees[J]. Fuzzy sets and systems, 1995, 69(2): 125-139. DOI:10.1016/0165-0114(94)00229-Z (  0) 0) |
| [11] |
WANG X Z, YEUNG D S, TSANG E C C. A comparative study on heuristic algorithms for generating fuzzy decision trees[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 2001, 31(2): 215-226. DOI:10.1109/3477.915344 (  0) 0) |
| [12] |
王进, 晏世凯, 高延雨, 等. 基于MPI的ML-kNN算法并行[J]. 郑州大学学报(理学版), 2018, 50(3): 34-38. WANG J, YAN S K, GAO Y Y, et al. Parallelization of ML-kNN Based on MPI[J]. Journal of Zhengzhou university (natural science edition), 2018, 50(3): 34-38. (  0) 0) |
| [13] |
RABCAN J, RUSNAK P, KOSTOLNY J, et al. Comparison of algorithms for fuzzy decision tree induction[C]//2020 18th International Conference on Emerging eLearning Technologies and Applications. Slovenia: IEEE Press, 2020: 544-551.
(  0) 0) |
| [14] |
杨蓓, 缑西梅, 艾艳. 专家系统中的模糊知识表示及推理研究[J]. 郑州大学学报(理学版), 2004, 36(2): 31-33. YANG B, GOU X M, AI Y. Study on the fuzzy knowledge representation and reasoning in expert system[J]. Journal of Zhengzhou university (natural science edition), 2004, 36(2): 31-33. (  0) 0) |
 2022, Vol. 54
2022, Vol. 54


