0 引言

随着微纳米制造技术的蓬勃发展, 晶体材料已广泛应用于集成电路、微机电系统(MEMS)以及其他微小电子器件等微/纳米系统中.实验研究^[1-2]发现, 微尺度金属单晶在塑性变形过程中应变会发生突变, 并且随着外部几何尺寸的减小, 应变突变现象会愈加明显^[3].从实际加工角度来看, 应变突变的发生使得亚微米尺度下的塑性变形难以控制^[4], 同时也给微机电技术当中的高精度金属切割和整体性能控制带来新的问题和挑战^[5], 成为事关微小器件高性能设计制备与安全使用的关键性问题.

目前, 微尺度晶体塑性的实验研究还处于发展阶段, 对于应变突变物理机制的解释和行为规律的揭示还存有争议^[6].另一方面, 针对微尺度晶体塑性特异性变形行为, 其理论描述也面临着新的挑战.一般情况下, 晶体塑性变形行为是用基于连续介质力学的晶体塑性滑移理论来描述, 但这种理论无法解释由于尺寸变小而出现的应变突变现象.因此, 揭示该尺度下晶体塑性变形的物理本质, 并预测其材料力学行为^[7]的理论分析模型将成为该研究的一个重点.

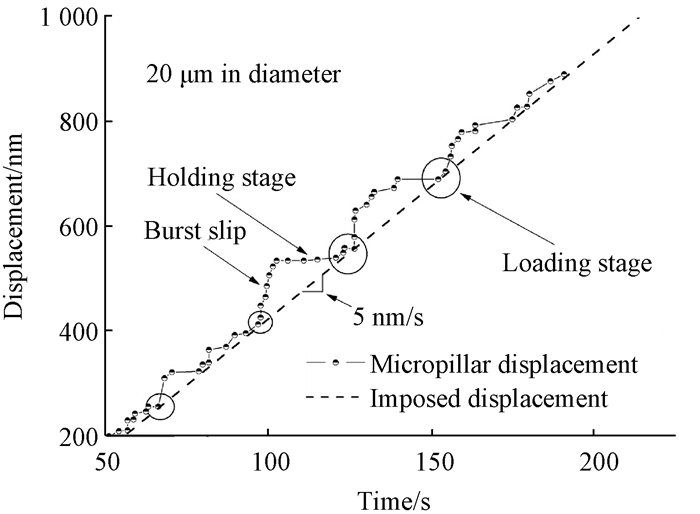
1 应变突变的实验现象

应变突变使得轴向压缩下的微柱体位移与压痕系统施加的位移并不完全同步^[8](如力加载、位移加载以及包含力加载与位移加载的混合加载模式), 图 1所示为混合加载模式下的情况.当微柱体位移与系统施加位移始终同步时, 即为一个恒应变率的加载过程.当某个时刻的微柱体位移开始超前于系统预设位移时, 塑性变形发生了一次突变滑移事件.之后, 位移-时间曲线往往存在一段水平或者斜率较小的位移线段, 这表明微柱体位移几乎没有发生变化, 因此处于一种变形停滞阶段.这种状态将一直持续到系统预设位移等于微柱体位移后结束, 因而使得塑性流动呈现出间歇性变化^[9].

一般来说, 应变突变的引发可能是由多种机制(如位错形核^[10]、位错拥塞结构崩塌^[11]等)共同作用或者轮流交替引发的, 并不完全受控于某一种机制而贯穿于整个塑性变形过程.一般情况下, 实验测试材料(微柱体)尺寸较大时, 应变突变受控于位错拥塞结构的崩塌, 其发生需要较低的应力水平；而在实验测试材料尺寸较小时, 应变突变受控于位错形核, 其发生则需要较高的应力水平^[12].

实验研究表明, 应变突变在时间上(如突变速度^[13])和空间上(如应变突变幅值^[14])都具有幂律分布特征.基于应变突变较为显著的有限尺寸效应^[15], 其幅值A的统计学分布^{[11, 14]}为P(A)~A^-τ·exp[-(A/A₀)²], 式中：P(A)为概率密度函数；τ为标度指数, 约等于1.35；A₀为突变幅值截断项, 是一个拟合参数^[15].

2 应变突变的理论模型 2.1 位错匮乏模型

位错匮乏理论模型^[10]假设晶体材料内的位错均为可移动位错.通过引入位错增殖率参数, 并设运动过程中的位错逃逸率为50%, 可得到总体位错密度的演化方程为

$ \rho = {\rho _0} + \frac{{\delta - 1/D}}{b} \cdot \frac{{{\varepsilon _{\rm{p}}}}}{M}, $

式中：D为微柱直径；b为伯格斯矢量；M为Schmid因子, 在模型建立时已知；ρ₀为初始位错密度^[3], 取值为1.0×10¹²~5.0×10¹³ m^-2；δ为位错增殖系数^[16], 取7×10⁵ m^-1；ε_p为塑性应变, 下标p表示塑性变形, ${\dot \varepsilon _{\rm{p}}} = \rho bv/M $, 其中v为位错运动速度, 大小可由文献[16]建立的理论方法确定.根据应变率方程$ {{\dot \varepsilon }_{\rm{p}}} = \frac{1}{E}\frac{{{\rm{d}}\sigma }}{{{\rm{d}}t}} + {{\dot \varepsilon }_{\rm{p}}}$(E为弹性模型；t为变形持续时间), 可建立应变ε与塑性流动应力σ的关系.

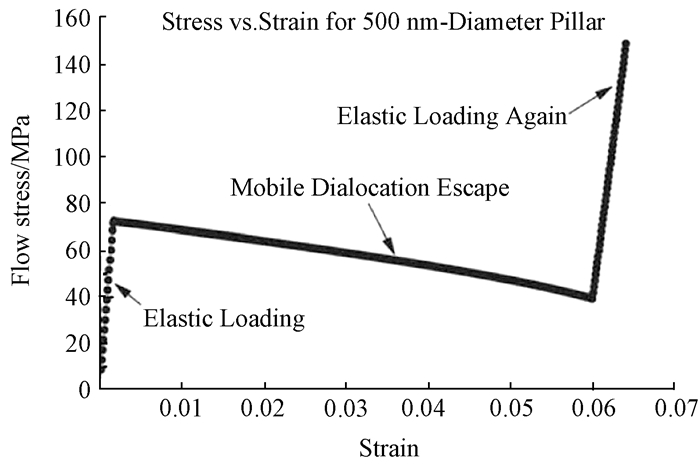
上述模型计算结果不仅能够表征块体材料稳定、光滑的塑性变形行为, 而且也能捕捉塑性流动过程中的应变突变事件, 具体表现在应力-应变曲线的应力下降现象, 如图 2所示.然而, 该模型在分析整个塑性流动过程中仅能捕捉到一次应变突变事件.此后, 塑性变形一直处于近似弹性的加载阶段.由于仅能获得一个应变突变幅值, 因而无法反映幅值的统计学变化规律, 这与实验观察到的离散的随机应变突变现象是不相符的.

2.2 位错源控制模型

位错源控制模型^[17]仍然假定可移动位错在运动过程的逃逸率为50%, 在位错增殖方面重新考虑了单臂位错源激活的影响.基于描述块体材料位错密度的演化方程, 获得了描述亚微米尺度微柱体塑性变形过程中的位错密度演化方程,

$ \frac{{{\rm{d}}\rho }}{{{\rm{d}}\gamma }} = \frac{1}{{2b\bar \lambda }} - \frac{{2{{\cos }^2}\left( {\beta /2} \right)}}{{bD}}, $

式中：γ为滑移系剪切应变；λ为单臂位错源有效长度, 其值可由文献[18]建立的理论关系式确定；β为滑移面法向与轴向的夹角, 在模型建立时已知; D为微纳米柱直径; b为伯格斯矢量, 为材料常数.等式右边第一项考虑了单臂位错源激活引起的位错密度变化; 第二项考虑了位错逃逸的影响.通过位错源截断硬化机制可将位错密度变化与微柱体塑性流动应力联系起来^[17], $ \sigma = ({\tau _{\rm{f}}} + 0.5Gb\sqrt \rho + \frac{{Gb}}{{\bar \lambda }})/M$, 其中:τ_f表示晶格摩擦力, 为材料常数; G为晶体材料的剪切模量, M为Schmid因子, 在模型建立时已知.

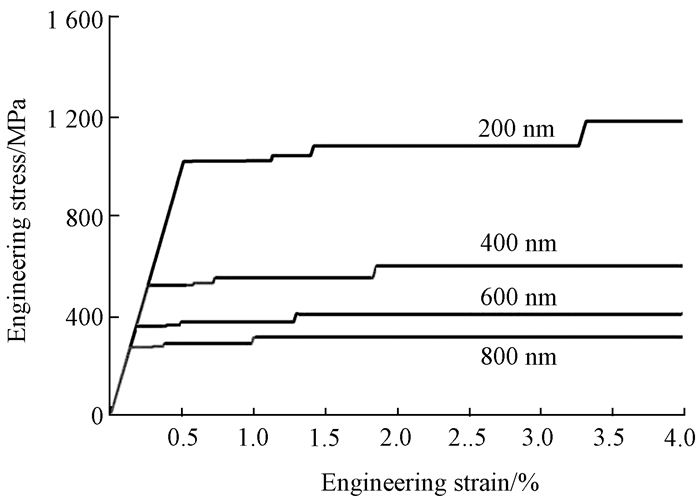
上述模型预测结果能够很好地再现亚微米尺度柱体间歇性塑性流动现象, 能够刻画实验中经常观察到的离散应变突变现象(如图 3).研究结果表明, 单臂位错源的激活与关闭会导致亚微米尺度晶体材料塑性变形呈现出间歇性变化.需要说明的是, 模型初始设定的位错密度与微纳米柱直径共同限制了该模型能够捕捉的应变突变事件个数, 因而无法较为完整地体现应变突变随机性分布规律.

2.3 蒙特卡洛模型

蒙特卡洛模型(Monte Carlo, MC)^[19]将微柱体的塑性流动分为应变突变和弹性加载两个部分.在某一应力水平下, 应变突变可能发生的概率为

$ {p_{m,{\rm{ }}n}} = [{S_n}({\sigma _{m - 1}}) - {S^n}({\sigma _m})]/{S^n}({\sigma _{m - 1}}), $

式中：p_{m, n}表示在第m增量步内, 发生第n次应变突变的概率; σ_m表示第m增量步内的当前应力水平; S_n(σ_m)表示在当前应力水平σ_m下未发生第n次应变突变的累计概率分布, 它可以通过微压缩实验测试获得.该模型认为, 应变突变发生时需要满足条件p_{m, n}≥c₁, 式中：c₁为系统生成的随机数, 0≤c₁≤1.否则, 弹性加载段发生, 应变增量为当前弹性应变增量.因此, 在某一应力增量步Δσ=σ_m-σ_m-1内, 应变增量Δε为

$ \Delta \varepsilon = \left\{ {\begin{array}{*{20}{l}} {A,}&{{\rm{ }}{p_{m,{\rm{ }}n}} \ge {c_1}}\\ {\frac{{{\sigma _m} - {\sigma _{m - 1}}}}{E},}&{{p_{m,{\rm{ }}n}} < {c_1}} \end{array}} \right.{\rm{ }}, $

式中A为应变突变幅值, 大小与当前应力水平σ_m有关, A=3.8×10^-5×exp(0.17×c₂×σ_m), c₂为系统生成的随机数, 0≤c₂≤1.

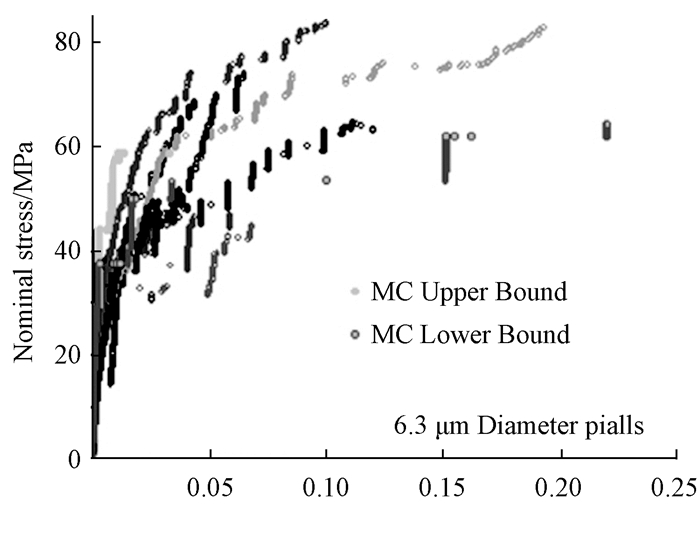
这一方法能够较为真实地表征实验过程中观察到的塑性流动间歇性, 突变幅值应力相关性以及突变幅值的幂律分布等实验现象(如图 4所示).需要说明的是, 该模型将应变突变在某个应力水平的发生概率(决定应变突变发生频率)以及突变幅值的应力相关性关系式(决定应变突变幅值), 作为初始输入参数(同样可以应用于其他加载方式的MC模拟当中^[19]).由于这些参数一般通过实验测试获得, 因而模拟结果能够反映应变突变随机性分布规律.

2.4 应变梯度模型

从目前已发表的参考文献来看, 描述应变突变现象的应变梯度模型主要包括两种.

一种观点认为微柱体的内应力场与二阶应变梯度相关, 并且呈现随机性挠动^[20].应变突变发生时, 往往涉及群体位错的运动, 其内部单根位错的应力场控制方程为

$ {\tau _{{\rm{ext}}}} + {\tau _{{\mathop{\rm int}} }}\left( {r,{\rm{ }}\gamma } \right) + {\tau _{{\rm{cor}}}}\left( \gamma \right) + \delta \tau \left( r \right) > 0, $

(1)

式中：r为空间坐标；τ_ext表示外部载荷施加的驱动力；τ_int表示因材料内部应变不协调引起的长程作用力；τ_cor表示群体位错之间施加的相互作用力；δτ为脉动应力, 表示位错自身运动引起的应力场变化, 大小服从高斯分布.上述控制方程中, τ_int与τ_cor的计算表达式中^[20]引入了二阶应变梯度, 大小均由局部应变γ确定.

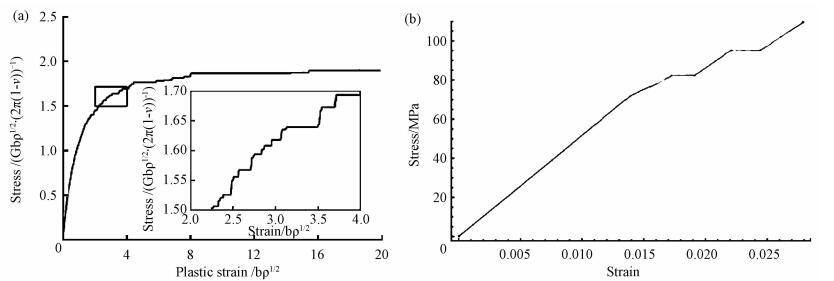
尽管该模型没有考虑应力与应变之间的关系, 也未考虑位错的演化特征, 但其预测的应力-应变曲线出现了明显的应变突变现象(如图 5(a)所示).此外, 由于应力场控制方程中的δτ幅值变化近似服从高斯分布, 导致基于该分布预测的应变突变幅值同样具有随机性, 呈现出实验观察到的应变突变幂律分布行为.

另一种观点认为^[21], 应变突变的发生与微柱体变形过程中所形成的剪切带有关, 这种剪切带的形成和扩展会导致微柱压缩应力-应变曲线的波动.基于这种物理变形机制, 该模型将微柱体划分为若干个滑移薄层, 构建了考虑不同滑移层的应变梯度塑性本构模型,

$ {\sigma _i} = \left\{ {\begin{array}{*{20}{l}} {E\varepsilon ,}&{{\rm{ }}\varepsilon \le \sigma _i^{\rm{s}}/E}\\ {\sigma _i^{\rm{s}} + \theta {\varepsilon _{\rm{p}}} - \theta {l^2}\frac{{{\partial ^2}{\varepsilon _{\rm{p}}}}}{{{\partial ^2}x}},{\rm{ }}}&{\varepsilon > \sigma _i^{\rm{s}}/E} \end{array}} \right., $

(2)

式中：E为晶体材料的弹性模量；σ_i^s表示第i个滑移层的屈服应力, 为材料常数, s表示屈服应力；θ为硬化系数, 是个拟合参数；ε_p为塑性应变；l为内禀材料长度, 等于滑移薄层的厚度, 在模型建立时已知.

通过模拟不同滑移层在不同应力水平下的表现, 该模型能够较为准确地表征应力-应变曲线上出现的应变突变现象(如图 5(b)所示).然而, 应用该模型需要事先设定滑移层的开动次序, 并且假设微柱体内部各个滑移层的微结构特征不同(屈服应力σ_i^s).当两个滑移层先后屈服时, 可认为发生了一个应变突变事件.通过增加滑移层的数目, 则可捕捉到更多数目的应变突变事件.此外, 通过考虑不同滑移层σ_i^s变化的随机性, 一些研究者建立了随机性应变梯度塑性模型^[22], 较为真实地描绘了应变突变的随机性变化行为, 而且能够反映硬化模量演化以及应变突变等材料微结构演化的基本特征.

2.5 晶体塑性滑移理论模型

晶体塑性滑移理论模型^[23-24]认为, 微柱体间歇性塑性流动过程可分为3个部分, 即加载段(下标l表示)、突变滑移段(下标b表示)和变形停滞段(下标h表示), 如图 1所示.该模型考虑了5个要素：

1) 边界条件.在加载段, 柱体位移与压痕系统施加位移保持一致, 则位移边界条件为$v = {{\dot \varepsilon }_0} \cdot L $, 式中：v表示柱体顶部的边界速度；L为柱体长度；${{\dot \varepsilon }_0} $为压痕测试系统所施加的恒应变率.在突变滑移段, 压痕系统施加的外载荷几乎不变, 同时位移发生了幅值为A的位移突变, 因此出现了混合边界条件f=0, u=A, 式中：f为柱体顶部所受的边界力；u为边界位移.根据式(1), 采用类似于文献[19]所使用的蒙特卡洛方法, 可以近似预测A的大小.在变形停滞段, 位移u和受力f均保持不变, 相应的边界条件为f=0, u=0.

2) 加载段和突变滑移段的区分.由于突变滑移段与力加载段的应变率特征不同, 需要将它们区分开来, 这可以通过引入一个平均剪切率来实现两者的分离.定义各段的平均剪切滑移率${\mathop {\bar \gamma }\limits^ \cdot } _\alpha \left( \xi \right)$^[23]为

$ {\mathop {\bar \gamma }\limits^ \cdot } _\alpha \left( \xi \right)=\left( {1 - \xi } \right)\dot \gamma _\alpha ^ + \left( t \right) + \xi \dot \gamma _\alpha ^ + \left( {t + \Delta t} \right), $

(3)

式中：上标“+”表示力加载段或者应变突变段的初始剪切应变率.ξ为无量纲常数, 当ξ取值较小时(通常ξ=0.2), 突变滑移段出现高应变率, 而加载段出现低应变率, 进而实现两个过程的分离.在应力-应变曲线中, 一个应变突变包含两个变形部分, 即突变滑移变形和变形停滞段.因此在方程(3)中, 当加载段发生时, Δt=Δt_l；当应变发生突变时, Δt=Δt_b+Δt_h.

3) 流动法则.晶体滑移变形可采用黏塑性描述,

$ {{\dot \gamma }_\alpha } = {{\dot \gamma }_0}{\mathop{\rm sgn}} ({\tau _{\rm{ \mathsf{ α} }}}/{g_{\rm{ \mathsf{ α} }}}){({\tau _{\rm{ \mathsf{ α} }}}/{g_{\rm{ \mathsf{ α} }}})^{m - 1}}, $

(4)

式中: ${{\dot \gamma }_0} $为参考应变率, 研究者通常取1.0×10^-3 s^-1；m表示率敏感指数, 是一个拟合参数；τ_α是α滑移系的分解剪应力；g_α为α滑移系的滑移硬化函数.式(4)可分别表述突变滑移段和力加载段的晶体滑移变形, 但所表述的物理意义并不相同^[23].此外, 变形停滞阶段的变形几乎为零, 可以忽略.

4) 应变突变判据.试样在加载段内承受压痕系统持续的加载, 产生的工程应力S₁满足$ {{\dot S}_1} \cdot {S_1}\left( t \right) > 0$, 而在突变滑移阶段, S₁满足$ {{\dot S}_1} \cdot {S_1}\left( t \right) \le 0$, 式中S₁可以通过轴向应力的体积平均计算.

5) 应变突变段的应力-应变关系.采用经典塑性理论框架^[25]来刻画应变突变段的塑性变形行为.当$ {{\dot S}_1} \cdot {S_1}\left( t \right) \le 0$时, 描述微柱体塑性变形行为的应力-应变关系式^[23-24]为$\Delta \sigma (\Delta t, \Delta {t_{\rm{b}}}) = \mathit{\Lambda }:\Delta \varepsilon \left( {\Delta t} \right) - \sum\limits_{\alpha = 1}^n {{\mathit{\Gamma }_\alpha }\Delta {\gamma _\alpha }(\Delta {t_{\rm{b}}})} $, 式中：Λ_ijmn=C_ijmn-σ_ijδ_mn, i、j、m、n代表四阶张量；Γ_α=C:p_α+w_α·σ-σ·w_α, 其中, C表示弹性模量张量, p_α和w_α分别为Schmid张量的对称部分和反对称部分；Δt_b可由关系式$\vec n \cdot \left\langle {\Delta \sigma \left( {\Delta t;\Delta {t_{\rm{b}}}} \right)} \right\rangle \cdot \vec n = 0 $确定.

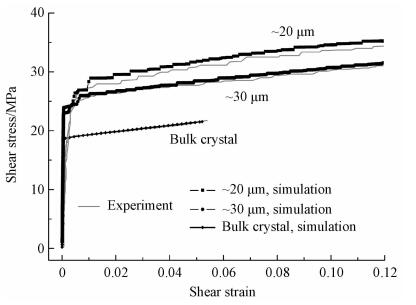
借助于有限元分析, 晶体塑性滑移理论模型预测的各个微米尺寸单晶柱体的应力-应变曲线结果如图 6所示.该模型能够描述从块体材料到微观柱体在轴向压缩下塑性变形方式的转变, 即从宏观金属材料稳定的塑性变形行为到微尺度间歇性塑性流动现象的变化.由于应变突变幅值变化的随机性, 因此该模型预测的塑性流动行为和实验结果保持完全一致是比较困难的.但是, 从模拟结果和实验测试曲线的高度相似性来看, 可以认为计算结果是合理的.

3 结论

本文重点关注亚微米尺度金属单晶的应变突变现象, 简要介绍了应变突变实验现象的一些研究成果, 讨论了近期基于特定物理变形机理相继发展的一些应变突变理论模型.从已发表的文献来看, 针对单晶微柱体的塑性变形的间歇性行为分析, 理论研究主要集中在直径10 μm以下, 所以本文最后重点介绍了适用于数微米尺寸以上的连续化晶体塑性理论模型, 并且阐述了当前理论模型的研究成果.

目前来看, 相对于实验测试和数值模拟在微尺度晶体塑性领域取得的进展, 理论研究的发展相对滞后.尽管目前已有的理论模型在捕捉应变突变方面取得了丰硕成果, 但还有待进一步探索和深入研究, 比如, 与应变突变密切关联的物理现象的理论描述(应变突变的应变率效应、应变突变的局部化变形方式等), 以及晶体塑性滑移理论的适用性范围的进一步扩展.