随着云计算的不断发展,外包数据库[1]为用户和企业提供了灵活的数据管理服务.然而外包数据库服务器是不可信的,数据拥有者将数据存储在外包数据库服务器上无法保证数据的安全性[2],即数据修改和查询结果的安全性.因此支持多用户操作数据的外包数据库可验证问题值得被关注.
目前大多数外包数据库可验证方案[3-6]只针对数据拥有者能够修改数据的场景,而不能满足多个用户操作数据库.原因有两个:第一,现有的方案使用认证数据结构[7-8](ADS)支持可验证计算服务,多用户场景会带来昂贵的计算代价;第二,现有的方案如果被拓展到支持多用户的安全性保证上,会给数据拥有者带来过重的负载.为了支持多用户操作的外包数据库的可验证计算,文献[9-10]提出了基于MHT (Merkle hash tree)的B树,但MHT结构主要的问题在于昂贵的维护代价.文献[11-12]给出了MR树(MR-tree)和XB树(XOR-B tree)的概念,实现了快速查询的完整性验证.文献[13-14]提出利用基于环签名的同态认证方式,当数据很大时成本很高,其扩展性受到了限制.文献[15-16]提出利用第三方审计实现多用户操作数据,但效率不高.文献[17]提出的方案则不能有效地对多用户进行管理.因此,目前仍然没有一个非常有效的方案来解决支持多用户操作的外包数据库可验证问题.
为解决目前外包数据库可验证方案不能满足多用户操作数据的问题,提出了一个支持多用户操作的外包数据库可验证方案.利用代理者集中处理所有用户的请求,实现对多用户的访问控制.利用基于身份标识的数据结构实现对数据进行修改,提高计算效率,解决认证数据结构带来的昂贵开销.利用数字签名算法和挑战应答的方式对查询结果进行验证,保证查询结果的完整性.
1 预备知识 1.1 双线性映射定义双线性映射生成算法[18]BilinearMapGen(1λ)→(e, g, G1, G2, p)生成一个双线性映射[17]e:G1×G1→G2,其中G1和G2是阶为p的乘法循环群,g是群G1的一个生成元,并且e满足3个属性:
1) 双线性.对于任意的P, P1, P2, Q, Q1, Q2∈G1,a, b∈Zp,满足
| $ e\left( aP, bQ \right)=e{{\left( P, Q \right)}^{ab}}, e({{P}_{1}}+{{P}_{2}}, Q)\\=e({{P}_{1}}, Q)\circ e({{P}_{2}}, Q), e(P, {{Q}_{1}}+{{Q}_{2}})\\=e(P, {{Q}_{1}})\circ e(P, {{Q}_{2}}). $ |
2) 非退化性.g1, g2为G1的生成元,即e不会将G1×G1中的所有元素都映射到G2的单位元上.
3) 可计算性.存在有效算法计算任意的e(P, Q).
双线性映射可根据超奇异椭圆曲线上的Weil和Tate配对来进行构造.
1.2 离散对数问题假设λ为安全参数,g是群G1的一个生成元,α∈Zp*,对于任意的敌手ADL, 满足Pr[ADL(g, gα)=α]≤negl(λ).
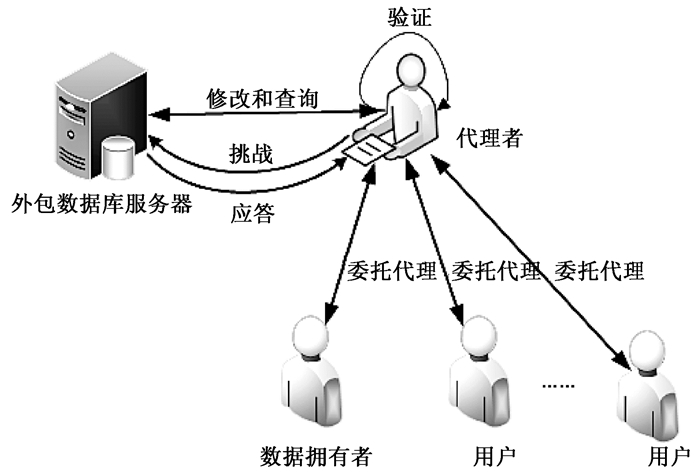
2 问题描述方案场景模型如图 1所示,系统包括四方实体:数据拥有者、普通合法用户、代理者和外包数据库服务器.
|
图 1 方案场景模型 Figure 1 Model of scheme |
1) 数据拥有者拥有原始数据,将数据上传至外包数据库服务器.
2) 普通合法用户通过代理进行数据的查询和修改.
3) 代理者对用户的权限进行验证,保证为合法的用户返回正确的查询结果.同时与外包数据库服务器进行交互,发送查询和修改请求,对数据进行数字签名,并利用数字签名对服务器返回的查询结果进行挑战应答,从而验证查询结果的正确性和完整性.
4) 外包数据库服务器为代理者返回查询数据并执行数据修改操作.
3 方案构造 3.1 模型定义本方案的模型由一个六元组算法{Setup, VerifyUser, Sign, GenChal, GenProof, VerifyProof}组成,各算法的具体描述为:
1) Setup(1λ)→(AK, u, q, H)初始化算法,由代理者执行.输入一个安全参数λ,输出算法所需要的全局参数(AK, u, q, H).
2) VerifyUser(name, SKname)→{0, 1}验证用户算法,代理者执行.将用户名name和私钥SKname作为输入,输出为0或1,0代表用户不合法,1代表用户合法.
3) Sign(v, tid, SK)→σv签名算法,由代理者执行.将数据v、数据的唯一标识tid和私钥SKname作为输入,输出为签名σv.
4) GenChal(I)→chal挑战算法,由代理者执行.将查询结果I作为输入,输出为挑战信息chal.
5) GenProof(chal, I)→φ生成证据算法,由服务器执行.将挑战信息chal和查询结果I作为输入,输出为证据φ.
6) VerifyProof(φ, δv, I)→{0, 1}验证算法,由代理者执行.将证据φ、签名σv和查询结果I作为输入,输出为0或1,0代表验证未通过,1代表验证通过.
3.2 安全性定义在这一节中,给出了方案的正确性和安全性定义.
3.2.1 正确性设λ为初始化选定的安全参数,D为数据库,定义checkUser算法为多项式时间算法,以用户名name、私钥SKname为输入,当用户合法时返回accept,否则返回reject,即checkUser(name, SKname)→{accept, reject};定义checkProof算法为多项式时间算法,以查询结果I、数据的签名δv、证据φ为输入,当查询结果确实为I时,返回accept,否则返回reject.定义支持多用户操作的外包数据库可验证方案是正确的,则要求各算法正确执行后,算法结果满足
| $ \begin{array}{l} Pr\left[ \begin{array}{l} VerifyUser(AK,name,S{K_{name}}) \to 0;\\ checkUser(name,S{K_{name}}) \to accept \end{array} \right] \le neg\left( \lambda \right),{\rm{ }}\\ Pr\left[ \begin{array}{l} VerifyUser(\varphi ,{\delta _v},I) \to 0;\\ checkProof(\varphi ,{\delta _v},I) \to accept \end{array} \right] \le neg\left( \lambda \right), \end{array} $ |
其中neg(λ)为可忽略函数.
3.2.2 安全性通过敌手A和挑战者β的挑战实验给出安全性定义.
挑战实验:定义敌手A试图通过以下步骤来伪造一个结果通过验证.
1) 挑战者β执行算法Setup,将密钥AK发送给A.
2) A向β进行查询,β向A返回查询结果I.
3) A对于特定的查询输出一个伪造的查询结果I*以及伪造的证据φ*.
4) 若VerifyProof(φ*, δv, I*)输出为1,且有I*≠I,则A伪造成功,否则伪造失败.
支持多用户操作的外包数据库可验证方案如果使得任意敌手A不能以不可忽略的概率赢得安全性实验:
| $ Pr\left[\begin{align} &Setup({{1}^{\lambda }})\to \left( AK, u, q, H \right);Sign\left( v, tid, SK \right)\to {{\sigma }_{v}} \\ &GenChal({{I}^{*}})\to chal;Adv(chal, {{I}^{*}})\to {{\varphi }^{*}} \\ &VerifyProof({{\varphi }^{*}}, {{\delta }_{v}}, {{I}^{*}})\to 1 \\ &checkProof({{\varphi }^{*}}, {{\delta }_{v}}, {{I}^{*}})\to reject \\ \end{align} \right]\le neg\left( \lambda \right), $ |
则称方案满足安全性.
3.3 方案详细描述 3.3.1 算法详细描述在多用户操作外包数据库场景下,考虑多个用户通过代理与外包数据库服务器交互的方式.方案具体算法描述如下.
1) Setup(1λ)→(AK, u, q, H)初始化算法.代理者首先调用BilinearMapGen算法生成安全参数AK=(e, g, G1, G2, p),随机选取G1中的两元素u和q,定义单向哈希函数H:{0, 1}*→Zp.
2) VerifyUser(name, SKname)→{0, 1}验证用户算法.代理者计算mk=gSKname,验证式(1)是否成立,
| $ mk=p{{k}_{name}}. $ | (1) |
表 1存储了合法用户的用户名及公钥,若式(1)成立,则代理者接受用户请求并输出1,反之,代理者拒绝用户请求并输出0.
|
|
表 1 用户名和公钥密码 Table 1 User name and public key |
3) Sign(v, tid, SK)→σv签名算法.代理者计算插入或更新的数据v的签名σv=(H(tid)·uv)SK.
4) GenChal(I)→chal挑战算法.设服务器返回查询结果为I={S1, …, Sc},代理者为每一个查询结果生成随机数mi,并输出挑战信息chal={(i, mi)}i∈I.
5) GenProof(chal, I)→φ生成证据算法.服务器首先计算R=e(u, pk)q.让μ′结合chal中的数据,计算
6) VerifyProof(φ, δv, I)→{0, 1}验证算法.代理者利用证据φ={R, μ, l}、生成的签名σv、查询结果I以及双线性映射e来验证式(2)是否成立,
| $ R\cdot e({{l}^{\gamma }}, g)=e({{(\prod\limits_{i={{S}_{1}}}^{{{s}_{c}}}{H}{{\left( tid \right)}^{{{m}_{i}}}})}^{\gamma }}\cdot {{u}^{\mu }}, pk), $ | (2) |
若式(2)成立,则该算法接受查询结果I,输出1;反之拒绝查询结果I,并且输出0.
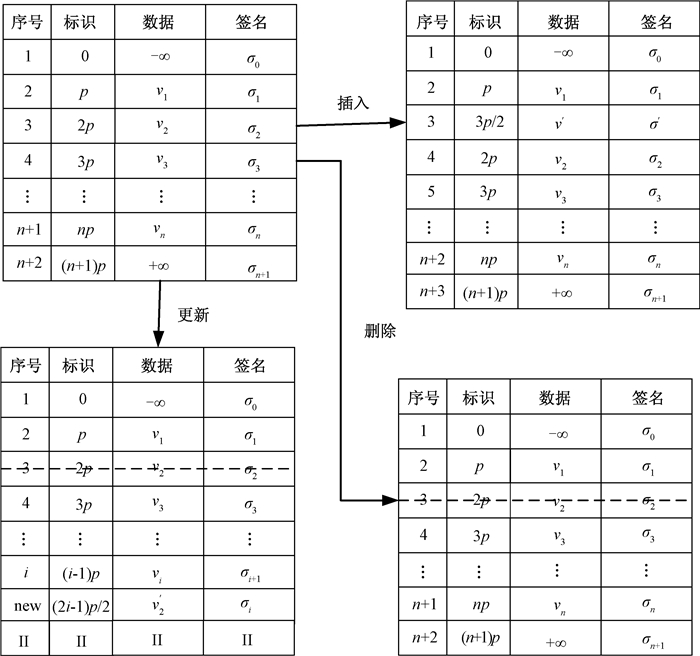
3.3.2 外包数据操作现存的外包数据库可验证方案中大多采用认证数据结构,在多用户场景会带来昂贵的计算代价,尤其是插入或删除数据时需要重新生成所有数据的签名,带来昂贵的维护代价,因此本方案构建了基于身份标识的数据结构机制(如图 2所示).使用此机制的好处在于插入一个新的数据时,不需要重新计算其他数据的标识,而且数据是有序存储的,如果vi>vj,则tidi>tidj.代理者被允许修改元组但无须改变其他元组的标识.这样就能够提高多用户场景下的计算效率,解决认证数据结构带来的昂贵开销.
|
图 2 数据修改操作 Figure 2 Operation of data update |
下面给出数据修改的几种形式.
1) 插入操作
如图 2所示,当代理者在v1和v2之间插入v′时,代理者向服务器发送插入请求,服务器插入数据并返回插入数据的前一个元组和后一个元组的唯一标识tid1=p和tid2=2p,代理者计算tid′=(tid1+tid2)/2作为v′的tid并通过Sign(v, tid, SK)→σv算法生成v′的签名,代理者将签名发送给服务器,服务器完成更新签名操作即完成了插入操作.
2) 删除操作
当代理者删除v2时,服务器删除数据v2,代理者将v2的签名值σv2设置成null,即完成了删除操作.若敌手试图进行重放攻击,服务器在生成证据计算认证信息l=σv2m2后不能通过验证.
3) 更新操作
在本方案中,更新操作等于一个删除操作和一个插入操作.代理者想要将v2变成v′2,即先删除v2,再在vi和vi+1中插入数据v′2.
4 安全性证明 4.1 正确性证明本方案是正确的,表示如果方案步骤都是正确执行,产生的结果都是按步骤执行得到的,没有被恶意篡改的,则代理者以极大概率接受结果,即代理者执行验证算法VerifyProof(φ, δ, I)→1.验证过程如下.
| $ \begin{align} &R\cdot e({{l}^{\gamma }}, g)=e{{\left( up, pk \right)}^{q}}\cdot e({{l}^{\gamma }}, g)=e({{u}^{q}}, pk)\cdot e({{(\prod\limits_{i\in I}{{{\sigma }_{{{v}_{i}}}}})}^{\gamma }}, g)= \\ &\text{ }e({{u}^{q}}, pk)\cdot e{{({{(\prod\limits_{i\in I}({H}(ti{{d}_{i}})\cdot {{u}^{v}})}^{SK}}^{^{{{m}_{i}}}})}^{\gamma }}, g)=~ \\ &e({{u}^{q}}, pk)\cdot e({{(\prod\limits_{i\in I}{H}{{(ti{{d}_{i}})}^{{{m}_{i}}}})}^{\gamma }}\cdot {{u}^{\sum\limits_{i\in I}{{{v}_{i}}{{m}_{i}}}}}, {{g}^{SK}})=~ \\ &e({{(\prod\limits_{i={{s}_{i}}}^{{{s}_{c}}}{H}{{\left( tid \right)}^{{{m}_{i}}}})}^{\gamma }}\cdot {{u}^{q+\sum\limits_{i\in I}{{{v}_{i}}{{m}_{i}}}}}, pk)=e({{(\prod\limits_{i={{s}_{i}}}^{{{s}_{c}}}{H}{{\left( tid \right)}^{{{m}_{i}}}})}^{\gamma }}\cdot {{u}^{\mu }}, pk). \\ \end{align} $ |
最后验证结果R·e(lγ, g)=e((
本方案满足不可伪造性,即敌手试图伪造正确信息,使得代理者通过验证是不可行的.
在认证授权即验证公钥阶段,假设敌手能够伪造私钥SK*,且使得代理者通过验证,即gSK*≠gSK 且VerifyUser(name, SK)→1,说明敌手通过公钥pk=gSK能够计算出私钥SK,与离散对数问题矛盾,说明敌手伪造私钥不成立.
在查询结果完整性验证阶段,假设敌手掌握了谕言机,可以伪造γ*=H(R),进而伪造证据φ*=(μ*, l, R),且能够使代理者通过验证,R·e(lγ*, g)=e((
| $ \begin{align} &R\cdot e({{l}^{\gamma-{{\gamma }^{*}}}}, g)=e({{(\prod\limits_{i={{s}_{i}}}^{{{s}_{c}}}{H}{{\left( tid \right)}^{{{m}_{i}}}})}^{\gamma-{{\gamma }^{*}}}}\cdot {{u}^{\mu-{{\mu }^{*}}}}, pk); \\ &{{l}^{\gamma -{{\gamma }^{*}}}}={{(\prod\limits_{i={{s}_{i}}}^{{{s}_{c}}}{H}{{\left( tid \right)}^{{{m}_{i}}}})}^{SK(\gamma -{{\gamma }^{*}})}}\cdot {{u}^{\alpha (\mu -{{\mu }^{*}})}}; \\ &{{({{\prod\limits_{i\in I}{{{\zeta }_{i}}}}^{{{m}_{i}}}})}^{\gamma -{{\gamma }^{*}}}}={{(\prod\limits_{i={{s}_{i}}}^{{{s}_{c}}}{H}{{\left( tid \right)}^{{{m}_{i}}}})}^{SK(\gamma -{{\gamma }^{*}})}}\cdot {{u}^{SK(\mu -{{\mu }^{*}})}};\text{ } \\ &{{u}^{SK(\mu -{{\mu }^{*}})}}={{(\prod\limits_{i\in I}{{}}({{\zeta }_{i}}^{{{m}_{i}}}/H\left( tid \right){{m}_{i}}SK))}^{\gamma -{{\gamma }^{*}}}}; \\ &{{u}^{SK(\mu -{{\mu }^{*}})}}=\prod\limits_{i\in I}{{}}{{({{u}^{SK{{v}_{i}}{{m}_{i}}}})}^{\gamma -{{\gamma }^{*}}}}; \\ &\mu -{{\mu }^{*}}=(\sum\limits_{i\in I}{{{v}_{i}}{{m}_{i}}})\cdot \gamma -{{\gamma }^{*}}; \\ &\sum\limits_{i\in I}{{{v}_{i}}{{m}_{i}}}=(\mu -{{\mu }^{*}})/(\gamma -{{\gamma }^{*}}). \\ \end{align} $ |
由于
保证授权阶段和查询完整性验证阶段的数据无法被伪造证明了本方案具有良好的安全性.
5 效率分析 5.1 理论分析以密码学操作(表 2)的方式估计计算成本.假设在查询的结果中包含c个随机块,在此基础上,以服务器计算和代理者计算的形式量化验证效率.在服务器端,生成的应答信息主要包括认证信息
| $ \begin{align} &cos{{t}_{\text{server}}}=c-MultEx{{p}_{{{G}_{1}}}}^{1}(\left| {{m}_{i}} \right|)+Pair_{{{G}_{1}}, {{G}_{2}}}^{1} \\ &+Ex{{p}_{{{G}_{1}}}}^{1}\left( \left| p \right| \right)+Has{{h}_{{{Z}_{p}}}}^{1}+Ad{{d}_{{{Z}_{p}}}}^{c}+Mul{{t}_{{{Z}_{p}}}}^{1}. \\ \end{align} $ | (3) |
|
|
表 2 密码学操作定义 Table 2 Notation of cryptography operation |
另一方面,代理者接收到证据φ=(μ, l, R)之后,对应的计算代价为
| $ \begin{align} &cos{{t}_{\text{client}}}=Has{{h}_{{{Z}_{p}}}}^{c+1}+Pair_{{{G}_{1}}, {{G}_{2}}}^{1}+Ex{{p}_{G}}^{3}\left( \left| p \right| \right) \\ &+Mult{{i}_{G}}^{2}+c-MultEx{{p}_{G}}^{1}(\left| {{m}_{i}} \right|). \\ \end{align} $ | (4) |
对比分析表明,在代理者方面需要比服务器计算出额外的ExpG12(|p|)+MultZp1+HashZpc,这些成本相比于双线性配对计算复杂性很小,因此可以忽略.
5.2 实验分析基于理论分析对本方案进行实验,运行实验程序的计算机配有3.40 GHz主频的处理器和8 GB内存,利用了Java pairing-based cryptography library实现双线性配对.将安全参数设置为160 Bit,查询数据块数量从c=0逐渐增加到c=800.
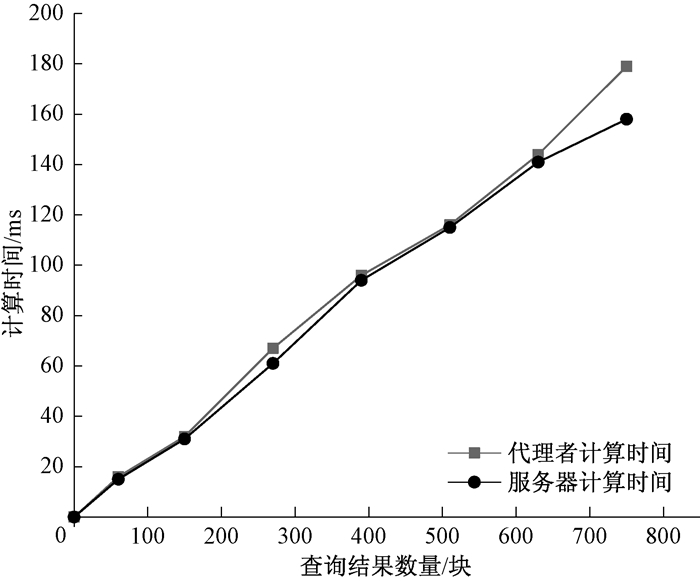
实验结果(如图 3所示)表明,代理者和服务器计算的成本基本相同,代理者执行验证算法,服务器执行计算算法,因此代理者的计算成本应该小于等于服务器的计算成本,因此实验数据表明该算法适合应用于多用户操作的外包数据库可验证方案中.
|
图 3 代理者和服务器的计算时间 Figure 3 Computation time of delegator and server |
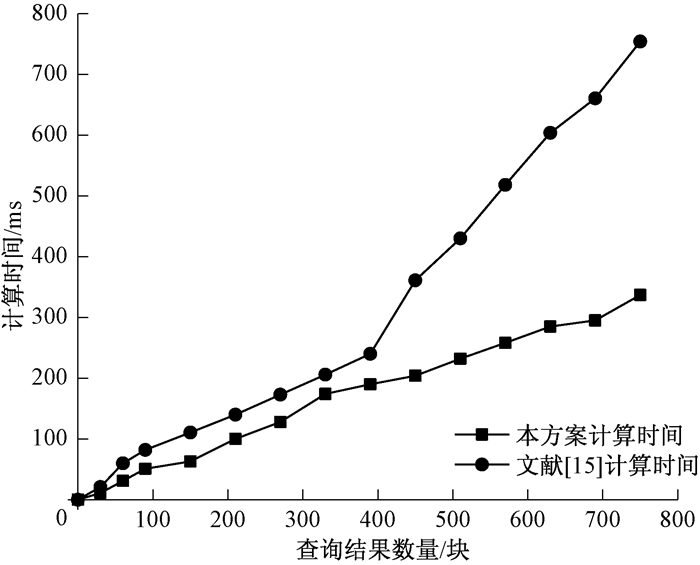
通过将本方案与文献[15]进行对比(如图 4所示),结果表明,随着查询结果数量的增加,本方案具有较高的效率.
6 结束语本文针对外包数据库的可验证方案中只能满足数据拥有者能够操作数据的问题,提出了支持多用户操作的外包数据库可验证方案,利用代理支持多用户管理,基于身份标识的数据结构动态修改数据,并利用数字签名保证了能够验证查询结果的完整性.效率分析和实验结果表明该方案能有效地满足需求,且具有很高的效率.
| [1] |
HACIGUMUS H, IVER B, MEHROTRA S. Providing database as a service[C]//International Conference on Data Engineering. Heidelberg, 2002: 29-38.
(  0) 0) |
| [2] |
KELLARIS G, KOLLIOS G, NISSIM K, et al. Generic attacks on secure outsourced databases[C]//ACM Sigsac Conference on Computer and Communications Security. Vienna, 2016: 1329-1340.
(  0) 0) |
| [3] |
JUELS A, KALISKI B S. Pors: proofs of retrievability for large files[C]//ACM Conference on Computer and Communications Security. Alexandria, 2007: 584-597.
(  0) 0) |
| [4] |
ATENIESE G, BURNS R, CURTMOLA R, et al. Provable data possession at untrusted stores[C]//ACM Conference on Computer and Communications Security. Alexandria, 2007: 598-609.
(  0) 0) |
| [5] |
SHACHEAM H, WATERS B. Compact proofs of retrievability[J]. Journal of cryptology, 2013, 26(3): 442-483. DOI:10.1007/s00145-012-9129-2 (  0) 0) |
| [6] |
BOWERS K D, JUELS A, OPERA A. Proofs of retrievability: theory and implementation[C]//ACM Cloud Computing Security Workshop. Toronto, 2009: 43-54.
(  0) 0) |
| [7] |
MILLER A, HICKS M, KATZ J, et al. Authenticated data structures, generically[C]//ACM Sigplan-Sigact Symposium on Principles of Programming Languages. San Diego, 2014: 411-423.
(  0) 0) |
| [8] |
汤鹏志, 张庆兰, 杨俊芳, 等. 一种新的无证书多代理签密方案[J]. 郑州大学学报(理学版), 2016, 48(2): 40-46. (  0) 0) |
| [9] |
LI F, HADJIELEFTHERIOU M, KOLLIOS G, et al. Dynamic authenticated index structures for outsourced databases[C]//ACM International Conference on Management of Data. Houston, 2008: 121-132.
(  0) 0) |
| [10] |
SINGH S, PRABHAKAR S. Ensuring correctness over untrusted private database[C]//International Conference on Extending Database Technology. Vienna, 2008: 476-486.
(  0) 0) |
| [11] |
YANG Y, PAPADIAS D, PAPADOPOULOS S, et al. Authenticated join processing in outsourced databases[C]//ACM SIGMOD International Conference on Management of Data. Providence, 2009: 5-18.
(  0) 0) |
| [12] |
YANG Y, PAPADIAS D, PAPADOPOULOS S, et al. Authenticated indexing for outsourced spatial databases[J]. The VLDB journal, 2009, 18(3): 631-648. DOI:10.1007/s00778-008-0113-2 (  0) 0) |
| [13] |
WANG B, LI B, LI H. Public auditing for shared data with efficient user revocation in the cloud[C]//IEEE International Conference on Computer Communications. Turin, 2013: 2904-2912.
(  0) 0) |
| [14] |
WANG B, LI B, LI H. Oruta: privacy-preserving public auditing for shared data in the cloud[C]//International Conference on Cloud Computing. Dubai, 2012: 295-302.
(  0) 0) |
| [15] |
YUAN J, YU S. Efficient public integrity checking for cloud data sharing with multi-user modification[C]//International Conference on Computer Communications. Toronto, 2014: 2121-2129.
(  0) 0) |
| [16] |
WANG C, WANG Q, REN K, et al. Privacy-preserving public auditing for data storage security in cloud computing[C]//International Conference on Computer Communications. San Diego, 2010: 525-533.
(  0) 0) |
| [17] |
SONG W, WANG B, WANG Q, et al. Tell me the truth: practically public authentication for outsourced databases with multi-user modification[J]. Information sciences, 2017, 387: 221-237. DOI:10.1016/j.ins.2016.07.031 (  0) 0) |
| [18] |
GALBRAITH S D, PATERSON K G, SMART N P. Pairings for cryptographers[J]. Discrete applied mathematics, 2008, 156(16): 3113-3121. DOI:10.1016/j.dam.2007.12.010 (  0) 0) |
 2018, Vol. 50
2018, Vol. 50