2. 复旦大学 计算机科学技术学院 上海 201203;
3. 哈尔滨工业大学(威海) 计算机学院 山东 威海 264209
2. School of Computer Science, Fudan University, Shanghai 201203, China;
3. College of Computer Science and Technology, Harbin Institute of Technology, Weihai 264209, China
E-Leaning(On-line Learning)是一种基于互联网的在线学习平台, 当前E-Learning站点有很多,比如edX、MOOC、coursegraph等,这类平台为学习者提供了大量有价值的教学资源.但是教学资源的多样化和复杂化使学生面临着信息选择的困难.因此,有必要设计和开发一种有效的数据管理算法和应用,用于分析数据之间存在的潜在联系,并从大规模数据中发现有价值的信息.
当前围绕数据管理方面的研究有很多,比如聚类分析、链路预测及相似性搜索等.文献[1]在2002年提出SimRank模型,将实体之间相似性定义为随机游走的期望相遇概率,以迭代形式计算实体之间的相似性.文献[2]考虑指入链接和指出链接计算实体之间的相似性,解决了相似性计算的“limited information”问题.文献[3]整合实体之间的任意相遇情况,解决了相似性计算的“zero similarity”问题.文献[4]通过忽略链接方向来发现实体之间任意方向的相遇情况,使相似性计算更加全面.文献[5]采用统一关系矩阵表示异构网络中的链接关系,采用迭代计算方式克服矩阵稀疏情况.文献[6]通过指定不同的元路径实现异构网络中的相似性计算,基于路径数度量实体之间的相似性.文献[7]将实体相似性转换为所关联的属性相似性,适用于X-Star网络的相似性计算.文献[8]能够计算不同类型实体之间的相关性,允许用户提供任意类型的实体进行查询.文献[9]结合维基百科中的文献网络和分类树来计算词语间的语义关联度.上述方法以迭代方式计算相似性,在相似性矩阵维护过程中需要很高的时间和存储开销.文献[10]表明,与基于文本的相似性搜索方法相比,这种基于链接关系的相似性搜索的返回结果更加符合人们的直观判断.
近年来研究者们围绕相似性搜索效率优化方面进行了大量研究[11-16].文献[11]采用关键节点对、局部和过滤阈值相似性三种方法来优化SimRank计算, 文献[12]通过避免局部偏和重复计算进一步优化了计算过程.文献[13]提出P-Rank异步积累更新算法,降低了处理器的等待时间.但这几种方法都需要维护大规模的相似性矩阵.文献[14]通过设计“seed germination”模型来优化“partial sums”的离线计算,依据“partial sums”的离线计算结果来提高在线相似性计算效率.文献[15]将图上的相似性搜索问题转化为在乘积图上寻找权威节点的问题.这两种方法降低了离线计算开销,但是会增加在线计算开销,降低查询处理效率.
本文在SimRank模型基础上提出一种高效的课程相似性搜索方法(CourseSim).主要贡献包括:1) 基于SimRank快速收敛特点,提出二次迭代模型,以降低相似性计算开销;2) 结合选修关系网络特征提出一种学习兴趣度量方法,用于去除弱链接关系,减少非必要的计算开销;3) 采用相似性累加计算的方法优化在线查询处理,以降低在线查询处理的时间开销;4) 在真实数据集上开展大量实验,在效率和效果两个方面进行了对比分析.
1 预备知识 1.1 选修关系网络E-Learning平台中的学生、课程以及两者之间的选修关系就构成了选修关系网络,记为G=(V, E).其中:V=VS∪VC,这里的VS和VC分别表示学生和课程类型的实体集合;E表示选修关系集合,有序对(s, c)∈E表示学生s∈VS和课程c∈VC之间的选修关系.
1.2 SimRank模型SimRank以递归的方式定义相似性,实体a, b∈V之间的相似性可定义为
| $ \mathit{\boldsymbol{S}}\left( {a, b} \right) = \frac{C}{{I\left( a \right)I\left( b \right)}}\sum\limits_{i = 1}^{\left| {I\left( a \right)} \right|} {\sum\limits_{j = 1}^{\left| {I\left( b \right)} \right|} {\mathit{\boldsymbol{S}}\left( {{I_i}\left( a \right), {I_j}\left( b \right)} \right)}, } $ |
其中:C∈(0, 1) 是阻尼因子,通常设置为0.8[1];I(a)表示为a的指入邻居的集合,|I(a)|为集合I(a)的元素数量.为了避免被除数为零,当I(a)或I(b)为空集时,约定S(a, b)为零.
SimRank以迭代方式计算相似性,实体a, b在第t次迭代的相似性记为Rt(a, b).当t=0时,如果a=b,那么R0(a, b)=1,否则R0(a, b)=0.当t=1, 2, …时,如果a=b,那么Rt(a, b)=1,否则
| $ {\mathit{\boldsymbol{R}}_t}\left( {a, b} \right) = \frac{C}{{I\left( a \right)I\left( b \right)}}\sum\limits_{i = 1}^{\left| {I\left( a \right)} \right|} {\sum\limits_{j = 1}^{\left| {I\left( b \right)} \right|} {{\mathit{\boldsymbol{R}}_{t-1}}\left( {{I_i}\left( a \right), {I_j}\left( b \right)} \right)} .} $ |
SimRank计算所有网络实体之间第t次迭代相似性的时间复杂度为O(t d2 n2),空间复杂度为O(n2),这里的n为网络中的实体数量,d为网络节点的平均度.
2 优化算法 2.1 选修关系网络的弱链接删除策略在选修关系网络中,如果某一门课程被很多学生所选,那么这门课程通常难以区分学生的学习兴趣,反之亦然.例如,“高等数学”、“大学英语”的选修学生数量很大,但这类课程属于通识课程,难以区分学生的学习兴趣.选修“数据挖掘”、“近似算法”的学生会相对较少,但这类课程往往属于专业课,更能区分学生的学习兴趣.课程c∈VC对学习兴趣的区分能力被形式化地表示为J(c)=1/N(c),式中N(c)表示选修关系网络中课程c的邻居集合.从学生角度来说,如果一门课程占学生选课的比重越大,则越说明学生对这门课程感兴趣.于是,学生s对于课程c的学习兴趣被形式化地表示为
SimRank在第t次迭代的相似性矩阵记为Rt.当t=0时,R0=In;当t=1, 2, …时,Rt=(CPRt-1P′)offdiag+In,其中:P表示实体之间的反向转移概率矩阵,矩阵元素为游走者沿着指入链接方向进行随机游走时的转移概率;P′表示P的转置;Moffdiag表示将矩阵M中的对角元素全部设置为零之后得到的矩阵;In为n×n的单位对角矩阵.基于矩阵运算,SimRank时间复杂度降低为O(t d n2),空间复杂度不变.
2.3 CourseSim计算模型SimRank具有快速收敛的特点,二次迭代的计算结果和收敛状态差别很小.课程相似性被定义为SimRank的二次迭代相似性.由于课程相似性计算仅需参考学生相似性,而且学生相似性计算也仅需参考课程相似性,这又可以进一步避免不必要的存储开销.课程相似性矩阵记为RC,计算公式为RC=C(PCSRSP′CS)offdiag+In,RS为学生相似性矩阵,计算公式为RS=C(PSCIncP′SC)offdiag+InS,其中:PCS表示课程和学生之间的转移概率矩阵,矩阵元素表示游走者从课程到学生沿着链接关系随机游走的转移概率;P′CS表示PCS的转置;Inc、InS分别表示nC×nC和nS×nS的单位对角矩阵,nC和nS分别表示选修关系网络中的课程和学生数量.
2.4 CourseSim计算算法为了进一步降低计算开销,相似性搜索过程分为离线和在线两个阶段.离线阶段依据选修关系网络计算学生相似性.在线阶段处理查询请求,基于学生相似性计算课程相似性.
2.4.1 离线计算算法算法1表示CourseSim的离线计算过程.采用累加的方式进行相似性计算,消除了零元素相乘操作对于时间开销的影响.学生和课程的平均度分别记为dS和dS′.由于矩阵PSC的行向量平均非零元素数与课程平均度相等,并且P′SC的行向量平均非零元素数与学生平均度也相等.因此,学生相似性计算的时间和空间开销都为O(dS dC nS).
算法1 CourseSim的离线计算算法.
输入:选修关系网络G;
输出:学生相似性矩阵RS.
for eachs∈VS
RS(s, s)←1;
for each c∈{cPSC(s, c)≠0}
for each s′∈{s′P′SC(c, s′)≠0\s}
RS(s, s′)←RS(s, s′)+CPSC(s, c)P′SC(c, s′);
end for
end for
end for
2.4.2 在线查询处理算法算法2表示CourseSim在线查询处理的基本算法.给定查询Q,首先计算Q与所有候选课程之间的相似性,最后返回top-k个最相似的课程.算法中的DCR(Q, *)用于存储C PCS(Q, *)RS的计算结果.算法平均时间开销为O(nC(dC+nD)),其中nD表示向量DCR(Q, *)的平均非零元素数.
算法2 CourseSim-baseline.
输入:选修关系网络G,矩阵RS,查询Q,参数k;
输出:top-k个最相似的课程.
RC(Q, Q)←1;
for each c∈VC\Q
DCR(Q, *)←C PCS(Q, *)RS
RC(Q, c)←DCR(Q, *)P′CS(*, c);
end for
选择top-k个最相似的课程,排序并输出.
2.4.3算法3表示在线查询处理的剪枝算法.该算法采用累加操作将RS中的非零元素累加至相似性计算结果.由于PCS的行向量平均非零元素数与课程平均度相等,P′CS的行向量平均非零元素数与学生平均度相等,所以在线查询的平均时间开销为O(dS dC nR),其中nR表示RS中非零行元素数.由算法1可知,RS的空间开销为O(dS dC nS),所以nR值为dS dC.因此,在线查询的平均时间开销为O(dC2dS2).
算法3 CourseSim-pruning.
输入:选修关系网络G,矩阵RS,查询Q,参数k;
输出:top-k个最相似的课程.
RC(Q, Q)←1;
for each s∈{s|PCS(Q, s)≠0}
for each s′∈{s′|RS(s, s′)≠0}
for each c∈{c|P′CS(s′, c)≠0\Q}
RC(Q, c)←RC(Q, c)+CPCS(Q, s)RS(s, s′)PCS′(s′, c);
end for
end for
end for
选择top-k个最相似的课程,排序并输出.
3 实验与结果 3.1 实验设置在机器配置方面,CPU为Intel(R) Core(TM) i5-4200,频率为2.30 GHz,内存为12.0 GB.开发环境为VS C++2010.实验在MOOC学院(http://mooc.guokr.com/)数据集上进行.采用网络爬虫抓取课程及学生信息,选择12 018位学生、2 195门课程、23 252条选修关系构建选修关系网络.实验对比方法包括SimRank[1]和P-Rank[2],采用文献[12]对两者计算过程进行优化.阻尼系数C设置为0.8,参数h设置为0.6.在效率评估方面,主要对比和分析离线计算和在线查询处理两个方面的计算开销.在效果评估方面,采用NDCG[16]评估相似性计算效果,依据返回结果中课程的排序及其对应相似性来计算第k个位置的NDCG值,效果评估的基准为SimRank相似性的精确值.
3.2 性能测试表 1表示离线计算相似性的时间开销.结果显示,CoureSim的时间开销低于SimRank和P-Rank的0.02%,这是因为CoureSim不需多次迭代,而且计算过程中没有涉及到零元素相乘的操作.表 2表示离线计算相似性的存储开销,这里的符号“M”是指“1 024*1 024”.结果显示,CourseSim相似性矩阵为SimRank和P-Rank在迭代次数为2时的40.42%,为在迭代次数为10时的22.63%.SimRank和P-Rank存储开销相同,这是因为选修关系是双向的,从而使两者的计算结果相同.
|
|
表 1 离线计算相似性的时间开销 Table 1 Time cost of off-line similarity computation |
|
|
表 2 相似性矩阵规模 Table 2 Scales of similarity matrices |
图 1表示CourseSim-baseline和CourseSim-pruning的查询处理时间.结果显示,当k增加时,查询时间的增加趋势并不明显,这是因为排序操作所需的时间开销远低于相似性计算过程.CourseSim-baseline的查询时间约为890 ms,约为CourseSim-baseline查询时间的6.01%.结果表明,本文提出的优化方法是可行的,能够减少在线查询的时间开销.
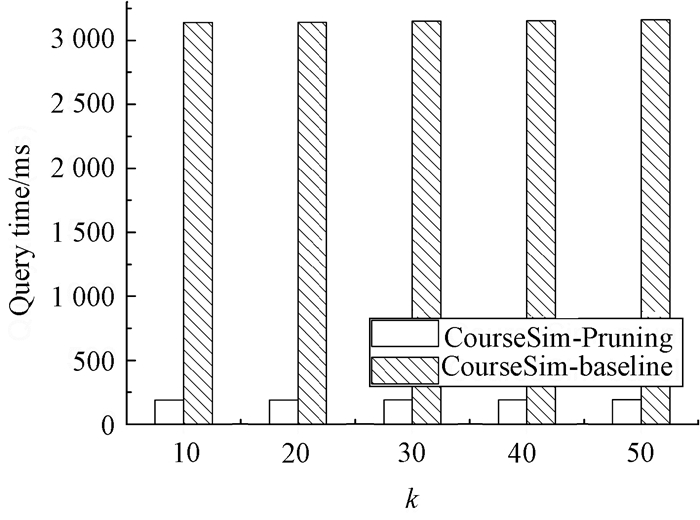
|
图 1 在线查询处理的时间开销 Figure 1 Time cost of on-line query processing |
图 2表示k取不同值时对应的NDCG,其中SimRank和P-Rank的迭代次数t=10.结果显示,SimRank和P-Rank的NDCG相同,表明两者在选修关系网络中具有相同的查询效果.当k发生变化时,SimRank值和P-Rank的NDCG值始终为1,这是因为经过10次迭代计算结果已经趋于收敛状态.CourseSim的NDCG值小于1,但是已经达到超过99.80%的NDCG值.当k从10到30增加时,CourseSim的NDCG值逐渐减小,当k取值从30增加到50时,又出现增加趋势,这是因为返回结果中排序第1的课程是查询本身,对应NDCG值为1,从而影响NDGG值的总体增加的变化趋势.
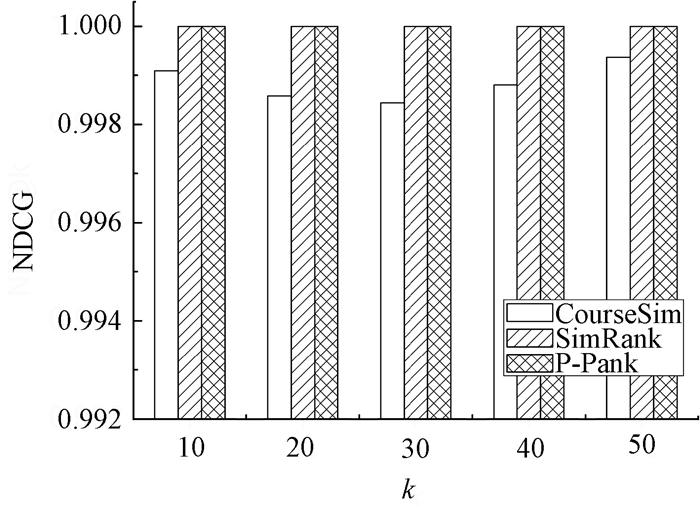
|
图 2 k取不同值时对应的NDCG Figure 2 NDCG value at different k |
表 3表示不同参数h对应的CourseSim的性能.在线查询阶段,仅记录返回top-50个课程时对应的查询时间和NDC值G,而且仅记录CourseSim-pruning的时间开销.分析可知,h值设置越低,离线计算时间及存储开销、在线查询时间也会越低.在效果测试方面,NDCG值随着参数h的降低而减小,这表明相似性计算结果和SimRank理论值之间的误差随着h增加而呈现增加的趋势.
|
|
表 3 参数h不同取值对应的CourseSim性能 Table 3 Performance of CourseSim on different h |
本文提出一种E-Learning平台中的课程相似性搜索算法,用于从大规模的教学资源中查找相似的课程.结合选修关系网络特征和SimRank快速收敛特点,对离线计算和在线查询处理两个阶段进行了优化.与现有方法相比,相似性计算过程不需多次迭代,显著降低了计算开销,返回结果的精确度损失低.未来研究工作将围绕个性化课程推荐展开,通过整合选修关系、用户评论等多方面的信息,结合聚类分析、社群挖掘等方法[17-18]研究课程推荐问题.
| [1] |
JEH G, WIDOM J. Simrank: a measure of structural-context similarity[C]//Proceedings of the Eighth ACM SIGKDD International Conferenceon Knowledge Discovery and Data Mining (SIGKDD2002). Edmonton, Alberta, 2002: 538-543. http://dl.acm.org/citation.cfm?id=775126
(  0) 0) |
| [2] |
ZHAO P, HAN J, SUN Y. P-Rank: a comprehensive structural similarity measure over information networks[C]//Proceedings of the 18th ACM Conference on Information and Knowledge Management(CIKM 2009). Hong Kong, 2009: 553-62. http://dl.acm.org/citation.cfm?id=1646025
(  0) 0) |
| [3] |
YU W, LIN X, ZHANG W, et al. More is simpler: effectively and efficiently assessing node-pair similarities based on hyperlinks[J]. Proceedings of the vldb endowment, 2014, 7(1): 13-24. (  0) 0) |
| [4] |
YOON S, KIM S, PARK S. C-Rank: a link-based similarity measure for scientific literature databases[J]. Information sciences, 2016, 326(1): 25-40. (  0) 0) |
| [5] |
XI W, FOX E A, FAN W, et al. Simfusion: measuring similarity using unified relationship matrix[C]//Proceedings of the 28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR 2005). Salvador, Brazil, 2005: 130-137. http://dl.acm.org/citation.cfm?id=1076034.1076059
(  0) 0) |
| [6] |
SUN Y, HAN J, YAN X, et al. PathSim: meta path-based top-k similarity search in heterogeneous information networks[J]. Proceedings of the vldb endowment, 2011, 4(11): 992-1003. (  0) 0) |
| [7] |
ZHANG M, HU H, HE Z, et al. top-k similarity search in heterogeneous information networks with X-Star network schema[J]. Expert systems with applications, 2015, 42(2): 699-712. DOI:10.1016/j.eswa.2014.08.039 (  0) 0) |
| [8] |
SHI C, KONG X, HUANG Y, et al. HeteSim: a general framework for relevance measure in heterogeneous networks[J]. IEEE transactions on knowledge & data engineering, 2014, 26(10): 2479-2492. (  0) 0) |
| [9] |
孙琛琛, 申德荣, 单菁, 等. WSR:一种基于维基百科结构信息的语义关联度计算算法[J]. 计算机学报, 2012, 35(11): 2362-2370. (  0) 0) |
| [10] |
MAGUITMAN A G, MENCZER F, ERDINC F, et al. Algorithmic computation and approximation of semantic similarity[J]. World wide web, 2006, 9(4): 431-456. DOI:10.1007/s11280-006-8562-2 (  0) 0) |
| [11] |
LIZORKIN D, VELIKHOV P, GRINEV M, et al. Accuracy estimate and optimization techniques for SimRank computation[J]. The VLDB journal, 2010, 19(1): 45-66. DOI:10.1007/s00778-009-0168-8 (  0) 0) |
| [12] |
YU W, LIN X, ZHANG W. Towards efficient SimRank computation on large networks[C]//IEEE 29th International Conference on Data Engineering (ICDE 2013). Brisbane, 2013: 601-612. https://www.computer.org/csdl/proceedings/icde/2013/4909/00/06544859-abs.html
(  0) 0) |
| [13] |
王旭丛, 李翠平, 陈红. 大数据下基于异步累积更新的高效P-Rank计算方法[J]. 软件学报, 2014, 25(9): 2136-2148. (  0) 0) |
| [14] |
KUSUMOTO M, MAEHARA T, KAWARABAYASHI K. Scalable similarity search for Simank[C]// International Conference on Management of Data (SIGMOD 2014), Snowbird, UT, 2014: 325-336. https://dl.acm.org/citation.cfm?id=2588555.2610526
(  0) 0) |
| [15] |
LEE P, LAKSHMANAN V S L, YU J X. On top-k structural similarity search[C]//IEEE 28th International Conference on Data Engineering (ICDE 2012). Washington, 2012: 774-785. http://dl.acm.org/citation.cfm?id=2310407
(  0) 0) |
| [16] |
RVELIN K, K EK, INEN J. Cumulated gain-based evaluation of IR techniques[J]. Acm transactions on information systems, 2002, 20(4): 422-446. DOI:10.1145/582415.582418 (  0) 0) |
| [17] |
李欣雨, 袁方, 刘宇, 等. 面向中文新闻话题检测的多向量文本聚类方法[J]. 郑州大学学报(理学版), 2016, 48(2): 47-52. (  0) 0) |
| [18] |
许长清, 赵华东, 宋晓辉. 基于大数据的电力用户群体识别与分析方法研究[J]. 郑州大学学报(理学版), 2016, 48(3): 113-117. (  0) 0) |
 2017, Vol. 49
2017, Vol. 49

