在深度学习中,大量标记数据对于神经网络的训练是至关重要的。但是对于许多深度学习的任务而言,获取这些标记数据是较为困难的,比如医疗任务中每一个标记都需要从专家的结论中得出。此外,通过网络获取的信息很大一部分是较为私密的,怎样标记这些数据也是一个复杂的问题。半监督学习[1]通过让模型从未标记数据中获取信息来减少对于标记数据的依赖,对于图像搜索、文本分类、文档检索[2]等任务,半监督学习都能取得很好的结果。近年来,半监督学习方法聚焦于在损失函数中增加损失项,这些损失项一般都是通过未标记数据取得的,促使模型更好地利用未标记数据中的信息来对数据进行分类。半监督学习方法可以大致分为熵最小化[3]、一致性正则化[4]与传统正则化[5]三类,但是已有方法往往很容易忽视数据互补信息与多阶段模型共同作用的优势。在上述研究基础上,本文提出一种新的半监督算法Mean Mixup,重新考虑模型生成伪标签的方法,通过多种数据增强方法使得模型能够学习数据的互补信息,并且让不同阶段的模型共同作用,最终让模型产生低熵预测来获取更准确的伪标签。为更好地应用一致性正则化,对标记数据和未标记数据进行混洗之后,根据数据类型传入不同的一致性损失函数,并使用比重系数调节来让模型能更好地从一致性正则化中受益。在常用数据集SVHN和CIFAR10上的实验结果验证了新算法的有效性,其在分类准确率上优于Pseudo-label、Π-model等半监督学习算法。
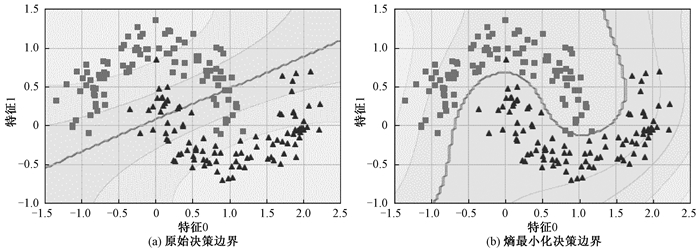
1 熵最小化与一致性正则化 1.1 熵最小化在深度学习中,聚类假设指出,模型的决策边界最好不通过边缘数据分布的高密度区域,也就是使得模型输出分布的熵尽可能小,这样会使模型获得更好的泛化性[6]。体现在学习过程中的熵最小化是让模型对目标数据的分类结果尽量自信,使得模型的决策边界尽量远离边缘数据点,同时让模型的拟合曲线更贴合数据的边缘分布。图 1对比了双月系统中原始决策边界与熵最小化约束下的决策边界。半监督学习算法中经常通过添加损失项来使得模型在未标记数据的概率分布实现熵最小化。Pseudo-label算法[3]对未标记数据进行预测,利用熵最小化获得置信度高的预测分布作为伪标签,并将其用作标准交叉熵损失的训练目标[2]。本文提出的Mean Mixup算法类似于Pseudo-label算法,都对未标记数据构建伪标签,不同之处在于Mean Mixup算法对如何得到伪标签进行了新的设计。
|
图 1 原始决策边界和熵最小化约束下的决策边界对比 Fig. 1 Comparison of original decision boundary and decision boundary under entropy minimization constraint |
一致性是指模型对受到扰动的数据点应输出相同的分布预测,半监督学习算法的很多突破性进展都是在一致性正则化基础上取得的。Π-model算法[4]通过在随机模型fθ(x)对同一样本的预测之间施加约束来实现一致性正则化。VAT算法[7]直接对输入x增加扰动,并且这种扰动能使得预测产生最大偏移,在受扰动样本与未受扰动样本产生的输出分布之间施加一致性约束。Mean teacher算法[8]通过构建教师-学生框架来实现一致性约束,在这个框架中使用了两个结构一致的网络,且教师网络的参数是学生网络参数的指数移动平均值,为更加直观,在本文中分别称为原型网络与指数网络。指数网络输入样本是对原型网络输入样本的加噪值,在两个网络的预测分布之间通过应用KL散度或者交叉熵函数来施加一致性约束。一致性正则化对于深度学习,尤其是半监督学习而言很有帮助,使得模型能够从标记数据的标签信息之外得到更多的高维特征信息。
2 Mean Mixup算法 2.1 算法概述本文在网络结构的选择上使用原型网络与指数网络,并在构建伪标签的方法以及一致性损失函数的计算上进行了创新。给定一个批次数的标记样本X和一个同等批次数的未标记样本U,Mean Mixup算法对未标记数据产生一个伪标签,从而得到带伪标签的U′。标记数据使用数据增强得到X′,X′与U′分别与两者连接而成的数据W使用数据混洗得到
| $ {L_{{\rm{loss}}}}{\rm{ = }}{L_x} + {\lambda _u}{L_u} + {\lambda _c}{L_{{\rm{con}}}}。$ | (1) |
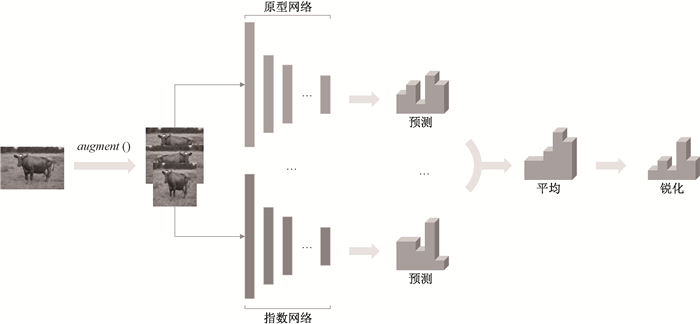
由于确认偏差[9]的原因,直接对未标记数据生成伪标签很容易对错误标签过度自信,从而不会继续从未标记数据中进行学习。Mean Mixup算法使用在同一模型的多个变种的共同作用下生成伪标签的方法,使伪标签的生成能获得多个角度的互补信息,对于未标记数据的判断更加可靠。为了得到未标记数据的软标签[10],使得未标记数据可以随着网络学习不断更新伪标签的生成结果,这种新的伪标签获取方法保证了网络能够从不同的角度和时间段受益,并逐渐提升伪标签的准确度。伪标签猜测流程如图 2所示。
|
图 2 伪标签猜测流程 Fig. 2 Pseudo label guessing process |
数据增强在半监督学习中能缓解标记数据的不足,而在Mean Mixup算法中也是生成伪标签的重要步骤。图 2显示了数据增强的几种变化。对于标记数据,数据增强后得到X′,其中x′=augment(x)。对于未标记数据,应用数据增强K次,得到未标记数据增强后的K个实例,
| $ {\hat q_1} = \frac{1}{{2K}}\sum\limits_{k = 1}^K {\left( {{P_{{\rm{model}}}}\left( {y|{{\hat u}_k};\theta } \right) + {P_{{\rm{ema - model}}}}\left( {y|{{\hat u}_k};\theta } \right)} \right)}。$ | (2) |
为了使网络可以获得更多不同角度的信息[11],使用不同时间段的网络对未标记数据进行预测。为了专注于获取原样本的特征信息,仅将原未标记数据传入其他时间段的网络,并进行如下计算:
| $ \hat q = \frac{1}{2}\left( {{{\hat q}_1} + {P_{n{\rm{ - model}}}}\left( {y|{{\hat u}_k}\theta } \right)} \right) $ | (3) |
其中:Pn-model(y|
| $ q = SharPen{\left( {\hat q, T} \right)_i} = \hat q_i^{\frac{1}{T}}/\sum\limits_{j = 1}^L {\hat q_j^{\frac{1}{T}}} , $ | (4) |
其中:T是超参数,T→0时锐化函数的输出趋近“one-hot”编码。文献[12]中指出,降低“温度(T)”有利于模型产生低熵预测。在运行过程中,算法对每一个批次的未标记数据都执行以上的方法计算伪标签,这种构建伪标签的方法使得伪标签的准确度随着模型学习不断提升。
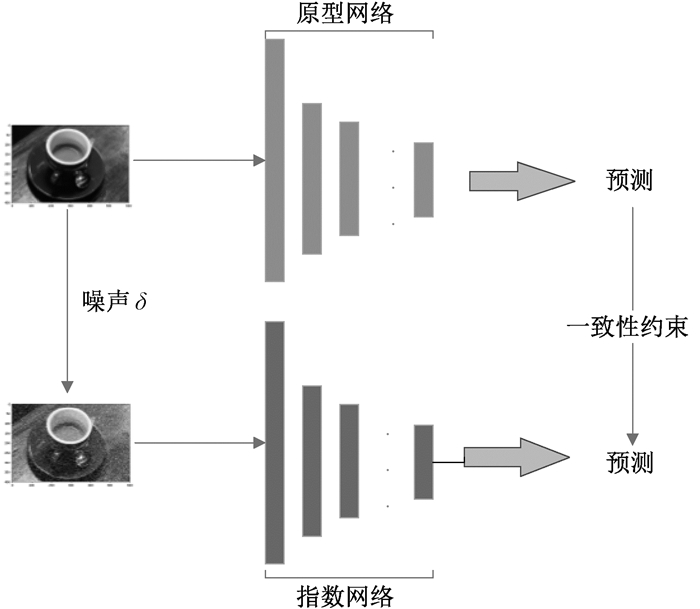
2.3 混洗数据的一致性约束一致性约束会使模型拥有更好的抗干扰能力,以往一致性约束通常是添加在网络的预测分布之间,区别是对输入样本加噪或者是网络参数的变化。但在很多应用中,标记数据与未标记数据经常出现分布不匹配,甚至某一类的标记样本数极少,模型难以获取足够的信息。对数据使用Mixup进行混洗来弥补两类数据之间的差异,使得模型学习的拟合曲线更符合数据分布,同时Mixup还实现了传统正则化对于网络的调节作用[13]。Mixup[12]中对于两个带标签的样本(x1,P1)和(x2,P2),其混合后的目标(x′,P′)为
| $ x' = \lambda '{x_1} + \left( {1 - \lambda '} \right){x_2};P' = \lambda '{P_1} + \left( {1 - \lambda '} \right){P_2}, $ | (5) |
其中:λ′=max(λ,1-λ),λ在Beta(α,α)内取值,α是超参数。W分别对X′和U′进行Mixup混洗,从而得到了新的数据
|
图 3 一致性约束的实现方式 Fig. 3 Implementation of consistency constraint |
未标记数据的一致性损失Lc1和标记数据的一致性损失Lc2可以分别表示为
| $ {L_{{c_1}}}{\rm{ = }}\frac{1}{{\left| {\hat u} \right|}}\sum\limits_{u, q \in \hat u} {\left\| {{P_{{\rm{ema - model}}}}\left( {y|u + \varepsilon ;\theta } \right) - {P_{{\rm{model}}}}\left( {y|u;\theta } \right)} \right\|_2^2} , $ | (6) |
| $ {L_{{c_2}}}{\rm{ = }}\frac{1}{{\left| {\hat x} \right|}}\sum\limits_{x, P \in \hat x} {\left\| {{P_{{\rm{ema - model}}}}\left( {y|x + \varepsilon ;\theta } \right) - {P_{{\rm{model}}}}\left( {y|x;\theta } \right)} \right\|_2^2}。$ | (7) |
模型通过损失函数Lloss来进行梯度计算并更新参数。式(1)中Lx为使用交叉熵函数计算的标记数据
| $ {L_x} = \frac{1}{{\left| {x'} \right|}}\sum\limits_{x, P \in x'} {H\left( {P, {P_{{\rm{model}}}}\left( {y|x;\theta } \right)} \right)}。$ | (8) |
Lu为使用L2损失函数计算的未标记数据
| $ {L_u} = \frac{1}{{L\left| {u'} \right|}}\sum\limits_{u, q \in u'} {\left\| {q - {P_{{\rm{model}}}}\left( {y|u;\theta } \right)} \right\|_2^2} 。$ | (9) |
损失函数中一致性损失项Lcon为Lc1与Lc2之和,即Lcon=Lc1+Lc2。损失函数中的未标记数据分类损失和一致性损失通过L2损失函数计算。L2损失函数与交叉熵不同,它是有界的,而且对完全错误的判断不太敏感,经常用作半监督学习中对未标记数据预测的损失以及预测结果不确定性的度量[14]。
3 实验结果及分析本文将提出的Mean Mixup算法在TensorFlow2.0平台上实现,并与Mean teacher[8]、VAT[7]、Π-model[4]、MixMatch[14]以及Pseudo-label[3]算法进行了比较。所有算法选择的网络均为“Wide ResNet-28-2”结构,但并没有使用学习率周期表而只使用了学习率衰减,选取运行100轮后得到的结果进行对比。Pseudo-label与MixMatch算法的对比结果是在TensorFlow2.0平台上进行复现得到的,其他算法的实验结果来自文献[15],选取的对比指标为错误率。MixMatch算法根据文献[14]选择超参数与学习率,并选取运行100轮后的结果作对比。
3.1 CIFAR10数据集CIFAR10是一个深度学习常用数据集,包含50 000张训练样本以及10 000张测试样本,每个样本都是32*32的RGB图片,并且分属于10个类别,类别各自独立,不会产生重叠。遵循常规半监督学习的设置,实验中使用了4 000个带标记的样本。设定Mean Mixup算法学习率为0.002,对输入图片只进行了归一化处理。结果表明,Pseudo-label、Mean teacher、VAT、Π-model、MixMatch算法的错误率分别为15.54%、15.87%、13.86%、16.37%、7.24%,而Mean Mixup算法的错误率仅为6.37%。从实验结果可知,在CIFAR10数据集中VAT算法比同样使用一致性正则化作为主要指导思想的Mean teacher算法表现要好,这可能是由于噪声的方向选择能够使得模型更好地学习。MixMatch和Mean Mixup算法的错误率比单纯一致性正则化的Mean teacher、VAT以及Π-model算法低,这证明了在半监督学习中使用熵最小化构建伪标签是有效的。为了对Mean Mixup算法进行更详细的实验论证,分别在CIFAR10数据集中选择了250、500、1 000、2 000个标签进行100轮的实验,算法的错误率结果分别为18.70%、14.86%、11.42%、7.64%。更少标签数据下的实验结果表明,在相同网络架构中,Mean Mixup算法在仅使用2 000个标记样本的情况下接近甚至超过经典半监督算法的表现,证明了Mean Mixup算法对于标签样本的利用率更高。
3.2 SVHN数据集SVHN数据集来源于谷歌街景门牌号码,经过裁剪成为32*32的RGB图片,包含73 257个训练样本和26 032个测试样本,被划分为10个类别,设定学习率为0.002。将Mean Mixup算法与经典半监督算法在使用4 000个标签样本运行100轮的实验结果进行了对比。结果表明,Pseudo-label、Mean teacher、VAT、Π-model、MixMatch算法的错误率分别为5.37%、5.65%、6.31%、7.19%、3.89%,而Mean Mixup算法的错误率仅为2.87%。在相同的标签数据下,Mean Mixup算法的分类错误率较其他半监督算法更低,并且相较于使用单一正则化的Pseudo-label等方法优势较为明显。同时,在CIFAR10数据集中比Mean teacher算法表现更好的VAT算法在SVHN数据集中并没有体现出优势,表明了在难以获得足够多的标签信息的半监督学习中,只使用一致性正则化或熵最小化很难获得出众的结果。为验证Mean Mixup算法在更少标签数据下的表现,进行了四组少标签(250、500、1 000、2 000个标签)数据实验,算法的错误率结果分别为9.13%、8.07%、6.58%、5.30%。Mean Mixup算法在只有2 000个标签数据的情况下依然取得了错误率为5.30%的成绩,这与4 000个标签数据下Pseudo-label算法的结果相近,且高于VAT和Π-model算法,再一次验证了Mean Mixup算法对于标签样本的利用率更高。
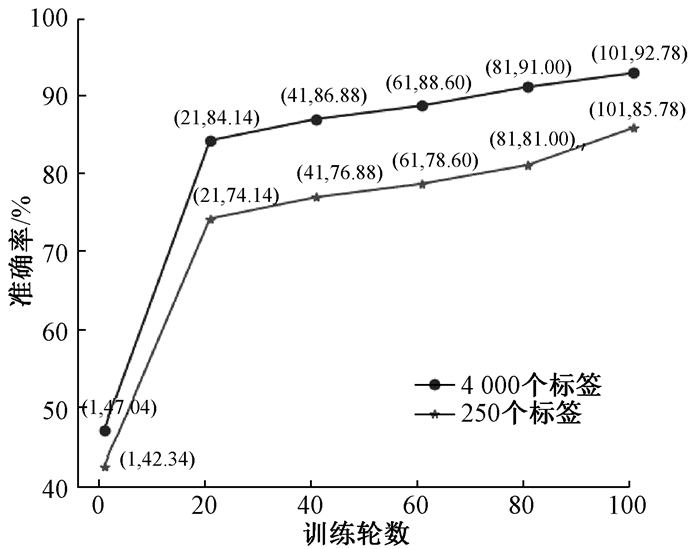
3.3 标签猜测准确度为了验证所得伪标签的准确度,将使用验证集猜测得到的标签与其自带的标签进行对比,每隔20轮记录下准确率,伪标签准确率结果如图 4所示。可以看出,通过集成数据互补信息进而获得低熵伪标签的方法是有效的,且在250个标签数据的情况下所得的伪标签准确率也达到了85.78%,与4 000个标签数据下的准确率差距不大,这表明Mean Mixup算法在标签数据稀少的情况下生成伪标签的准确度依然较高。
|
图 4 伪标签准确率结果 Fig. 4 Pseudo label accuracy results |
在Mean Mixup算法中有四个较为重要的超参数,分别为未标记数据增强次数K、Mixup中取样区间λ以及未标记数据分类损失与一致性损失各自的比重系数λu和λc。为了更直观地展示超参数的选择,同时避免超参数细微变化所带来的不公平的性能比较,仅选择了四组超参数在数据集中进行实验,其中依照MixMatch算法中的设置使得α=0.75,遵循Mean teacher算法使得λc=1。对于每组超参数,均使用4 000个标签,所应用的数据预处理方式与优化器都是一致的,最终选取其运行100轮后的错误率来进行对比。结果表明:K=1, λu=75时错误率为7.37%;K=1, λu=150时错误率为7.86%;K=2, λu=75时错误率为6.37%;K=2, λu=150时错误率为6.65%。从四组不同超参数对比实验结果中可以看出,未标记数据增强次数K对于结果的影响较大,这是由于在生成伪标签的过程中,多个不同增强实例的反馈能增强伪标签的准确度。而一致性损失值在实验过程中一直较小,需要使用较大的比重系数才能使网络从一致性损失中进行学习,所以直接从75增大到150对于实验结果的影响也不明显。因此,对比实验中超参数的选择为K=2,α=0.75,λu=75,λc=1。
4 结论本文针对以往半监督算法往往忽略数据互补信息的不足,提出了一种新的半监督算法Mean Mixup。该方法能够有效利用少量标签带来的信息,并推广到未标记数据上。Mean Mixup算法基于熵最小化与一致性正则化的思想,设计了通过多阶段模型共同作用,集成多角度信息从而生成低熵伪标签的方法,并利用一致性正则化优化了模型的分类性能。在经典数据集CIFAR10和SVHN上与现有的半监督算法进行了比较,实验结果表明,在相同标签数的情况下,Mean Mixup算法的分类准确度较之前的半监督方法表现更好。即使在更少标签数据的情况下,Mean Mixup算法获得的准确度也超过了之前使用单一正则化的半监督方法。本文还验证了生成伪标签的准确度,发现即使在标签数据稀少的情况下,生成伪标签的准确度依然较高,表明Mean Mixup在解决半监督学习问题上是有效的,且集成数据信息生成伪标签的方法是正确的。
| [1] |
ZHU X J, GOLDBERG A B. Introduction to semi-supervised learning[M]. San Rafael: Morgan and Claypool Publishers, 2009.
(  0) 0) |
| [2] |
刘欢, 徐健, 李寿山. 基于变分自编码器的情感回归半监督领域适应方法[J]. 郑州大学学报(理学版), 2019, 51(2): 47-51. LIU H, XU J, LI S S. A semi-supervised domain adaptation method of sentiment regression on variational autoencoder[J]. Journal of Zhengzhou university (natural science edition), 2019, 51(2): 47-51. (  0) 0) |
| [3] |
ISCEN A, TOLIAS G, AVRITHIS Y, et al. Label propagation for deep semi-supervised learning[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2019: 5070-5079.
(  0) 0) |
| [4] |
LAINE S M, AILA T O. Temporal ensembling for semi-supervised learning: US20180101768[P]. 2018-04-12.
(  0) 0) |
| [5] |
ELAD M, DATSENKO D. Example-based regularization deployed to super-resolution reconstruction of a single image[J]. The computer journal, 2009, 52(1): 15-30. (  0) 0) |
| [6] |
WANG F, ZHANG C S. Label propagation through linear neighborhoods[J]. IEEE transactions on knowledge and data engineering, 2008, 20(1): 55-67. DOI:10.1109/TKDE.2007.190672 (  0) 0) |
| [7] |
MIYATO T, MAEDA S I, KOYAMA M, et al. Virtual adversarial training: a regularization method for supervised and semi-supervised learning[J]. IEEE transactions on pattern analysis and machine intelligence, 2019, 41(8): 1979-1993. DOI:10.1109/TPAMI.2018.2858821 (  0) 0) |
| [8] |
TARVAINE A, VALPOLA H. Mean teachers are better role models: weight-averaged consistency targets improvesemi-supervised deep learning results[C]//Proceedings of the Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2017: 1195-1204.
(  0) 0) |
| [9] |
ZHANG Z, RINGEVAL F, DONG B, et al. Enhanced semi-supervised learning for multimodal emotion recognition[C]//Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE Press, 2016: 5185-5189.
(  0) 0) |
| [10] |
TANAKA D, IKAMI D, YAMASAKI T, et al. Joint optimization framework for learning with noisy labels[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE Press, 2018: 5552-5560.
(  0) 0) |
| [11] |
HAO X, ZHANG G G, MA S. Deep learning[J]. International journal of semantic computing, 2016, 10(3): 417-439. DOI:10.1142/S1793351X16500045 (  0) 0) |
| [12] |
GUO H Y, MAO Y Y, ZHANG R C. Mixup as locally linear out-of-manifold regularization[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto: AAAI Press, 2019, 33: 3714-3722.
(  0) 0) |
| [13] |
LAKSHMINARAYANAN B, PRITZEL A, BLUNDELL C. Simple and scalable predictive uncertainty estimation using deep ensembles[C]//Proceedings of the Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2017: 6402-6413.
(  0) 0) |
| [14] |
BERTHELOT D, CARLINI N, GOODFELLOW I, et al. MixMatch: a holistic approach to semi-supervised learning[C]//Proceedings of the Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2019: 5049-5059.
(  0) 0) |
| [15] |
OLIVER A, ODENA A, RAFFEL C A, et al. Realistic evaluation of deep semi-supervised learning algorithms[C]//Proceedings of the Advances in Neural Information Processing Systems. Cambridge: MIT Press, 2018: 3235-3246.
(  0) 0) |
 2021, Vol. 53
2021, Vol. 53


