语音是人类最重要、最有效、最常用的交流方式之一,在生产生活中起着非常重要的作用。语音重建是指从语音信号的变换域或参数域重建时域信号的过程[1],在语音信号处理中占据非常重要的地位。
传统的语音信号处理是基于Nyquist采样定理,该定理指出,对一段语音信号采样时,采样频率至少需要达到信号带宽的两倍,才能保证在接收端完美重建出原始信号。但随着大数据时代的到来,人与人之间的联系更加密切,信息交互也更加频繁,这就意味着需要传输、存储的语音信号的数据量爆炸式增长,使得语音信号处理系统越来越难以承受。
压缩感知(compressed sensing, CS)[2]理论的出现彻底打破了传统的信号采样方式。CS理论指出,如果信号是稀疏的或在某个变换域内是稀疏的,那么就可用一个与变换域不相关的观测矩阵将高维信号投影到一个低维空间上,得到观测向量,然后在重建端通过求解优化问题从观测向量中高概率地重建原始信号[3]。与Nyquist采样定理不同,CS理论对信号实行边采样边压缩处理,降低了采样率,缩减了需要存储的数据量。因此压缩感知理论被广泛应用于语音信号处理[4]、图像信号处理[5]以及无线电信号处理。
CS理论主要包含三部分:信号的稀疏表示、测量矩阵的设计和重建算法。其中重建算法是该理论能否实现的关键[6]。目前,重建算法主要分为贪婪类算法和凸优化类算法[7]。由于贪婪类算法计算复杂度低、时间短,在实际工程运用中较为广泛。阶段性弱选择正交匹配追踪(SWOMP)算法是Blumensath等提出的一种经典贪婪算法[8],该算法不需要将信号的稀疏度作为先验条件,而是利用阈值策略筛选原子,完成信号的重建,适合应用在语音信号这种稀疏度不易求得的信号中。
SWOMP算法重建信号时,采用内积准则从传感矩阵中挑出与残差信号最匹配的原子。内积匹配准则的实质是通过计算两个向量夹角的余弦值表示两个向量的相似程度。但是使用内积准则计算向量相似度时,不会放大数据对象的重要部分,在传感矩阵中存在任意两个相似原子都会影响匹配过程,导致原始信号的部分信息丢失,造成算法重建精度下降[9]。因此本文针对SWOMP算法在原子匹配过程存在原子丢失的缺点,提出用广义Jaccard系数相似性匹配准则代替内积准则,完成原子相似性的度量,优化原子选择,以此提高语音信号重建的质量。
1 压缩感知基本内容压缩感知理论指出,假设x是长度为Ψ的原始信号,若该信号是稀疏的或在某一稀疏基上能够被稀疏表示,那么可以将该稀疏信号投影到满足约束等距(restricted isometry property,RIP)[10]条件的M×N的观测矩阵Φ(M≪N) 上,得到大小为M×1观测值y,即:
| $ y=\boldsymbol{\varPhi} x。$ | (1) |
若原始信号在时域上不稀疏,则可以通过N×N的稀疏基Ψ进行稀疏表示,即:
| $ x=\boldsymbol{\varPsi}{\boldsymbol{\nu}}, $ | (2) |
其中:ν是N×1的经过稀疏表示后的稀疏系数,当ν满足‖ν‖0=K(K≤N) 时,称信号x是K稀疏的,‖ν‖0表示向量ν的零范数,即向量ν中的非零元素个数。此时式(1)可写为
| $ y=\boldsymbol{\varPhi} \boldsymbol{\varPsi}{\boldsymbol{\nu}}=\boldsymbol{A} \theta, $ | (3) |
A=ΦΨ,A为传感矩阵。RIP描述为对于任意严格K稀疏的向量η,若存在常数δK∈(0, 1) 使得
| $ \left(1-\delta_{K}\right)\|\boldsymbol{\eta}\|_{2}^{2} \leqslant\|\boldsymbol{\varPhi} \boldsymbol{\eta}\|_{2}^{2} \leqslant\left(1+\delta_{K}\right)\|\boldsymbol{\eta}\|_{2}^{2} $ | (4) |
成立,则称矩阵Φ满足K阶约束等距特性。
信号重建是压缩感知的最重要的一个环节,压缩感知重建信号实质就是由式(1)求解最小L0范数的优化问题,即
| $ \min \|\boldsymbol{\nu}\|_{0} \text {, s. t. } \boldsymbol{y}=\boldsymbol{\varPhi} \boldsymbol{x}=\boldsymbol{\varPhi} \boldsymbol{\varPsi} \boldsymbol{\nu}=\boldsymbol{A} \boldsymbol{\nu}, $ | (5) |
其中:‖ν‖0是ν的L0范数。
目前以L0范数最小化为基础的经典贪婪类算法有OMP算法[11]、ROMP算法[12]、SWOMP算法等重建算法。
2 基于广义Jaccard系数的SWOMP语音重建 2.1 分段弱正交匹配追踪算法SWOMP算法在每次迭代的过程中,首先要确定残差信号的成分;然后以内积准则为度量手段,在传感矩阵中选出最能逼近这些成分的原子用于更新支撑集,将支撑集内的原子通过求最小二乘法完成信号的逼近,最后求得新的残差值。
假设索引集为Ω,则有
| $ \left|{sim}\left(\boldsymbol{A}_{i}, \boldsymbol{r}\right)\right| \cdots\left|{sim}\left(\boldsymbol{A}_{j}, \boldsymbol{r}\right)\right|, $ | (6) |
式中:sim( )函数代表两个向量之间的相似程度;r表示残差;Ai、Aj 代表传感矩阵的列向量,将筛选的最优原子的位置保存在索引集Ω中。
内积匹配准则
| $ u_{i}=\operatorname{argmax}\left|\left\langle\boldsymbol{A}_{i}^{\mathrm{T}}, \boldsymbol{r}_{s-1}\right\rangle\right| u_{i} $ | (7) |
是用内积准则度量相似性,计算传感矩阵中与残差值最相似的原子,内积模值越大,表示原子与残差值的相似程度也越大。ui代表当前迭代过程中与残差值最相似的原子。从上述分析可知,信号重构实质是通过最优原子构建的支撑集完成重构,因此最优原子的选择对重构算法至关重要。但是以内积准则筛选原子的传统SWOMP算法很难选出最优的原子,造成重构语音信号的质量差。
2.2 基于广义Jaccard系数的分段弱正交匹配追踪算法对任意两个n维向量x、y,内积匹配准则为
| $ {sim}(\boldsymbol{x}, \boldsymbol{y})=\frac{\langle\boldsymbol{x}, \boldsymbol{y}\rangle}{\|\boldsymbol{x}\| \cdot\|\boldsymbol{y}\|}=\frac{\sum\limits_{i=1}^{n} \boldsymbol{x}_{i} \cdot \boldsymbol{y}_{i}}{\sqrt{\sum\limits_{i=1}^{n} \boldsymbol{x}_{i}^{2} \sum\limits_{i=1}^{n} \boldsymbol{y}_{i}^{2}}} \text { 。} $ | (8) |
内积准则实质是通过计算两个向量夹角的余弦值来表示向量的相似性,余弦值越大,夹角越小,向量就越相似。传统SWOMP算法便是使用内积准则度量残差与原子间相似性。但是该匹配准则不容易区分相似向量,存在原始信号部分丢失的问题,导致算法的重建效果不理想。为了解决该问题,本文提出将广义Jaccard系数引入到最佳原子匹配过程中。
对任意两个n维向量x、y,广义Jaccard系数匹配准则为
| $ {Jaccard}(\boldsymbol{x}, \boldsymbol{y})=\frac{\sum\limits_{i=1}^{n} \boldsymbol{x}_{i} \boldsymbol{y}_{i}}{\sum\limits_{i=1}^{n} \boldsymbol{x}_{i}^{2}+\sum\limits_{i=1}^{n} \boldsymbol{y}_{i}^{2}-\sum\limits_{i=1}^{n} \boldsymbol{x}_{i} \boldsymbol{y}_{i}}。$ | (9) |
由式(8)、(9)可知,广义Jaccard系数匹配准则的分母前半部分可以看作是两个向量平方的算数平均,而内积准则的分母是两个向量平方的几何平均,由数学知识可知,算数平均比几何平均能更好地保留每个分量的原始状态,同时广义Jaccard系数匹配准则分母的后半部分可以看作是在向量算数平均的基础上减去两个向量的相同部分,进一步凸显了两个向量之间的差异,使得原子不容易混淆[13]。因此,理论上广义Jaccard系数匹配准则的引入能够选出更优的匹配原子,进而提高算法的重建精度。
将广义Jaccard系数匹配准则引入SWOMP算法,提出基于广义Jaccard系数的SWOMP算法,改进算法的匹配准则为
| $ u={abs}\left[{Jaccard}\left(\boldsymbol{A}^{\mathrm{T}}, \boldsymbol{r}_{s-1}\right)\right],$ | (10) |
式中:Jaccard(AT,rs-1) 为残差和传感矩阵列向量的广义Jaccard匹配系数。
基于广义Jaccard系数的匹配准则能够突出向量的组成元素,更多地保留每个向量的原始特征,解决了内积准则度量相似性时原始信号部分丢失的问题,筛选出与残差向量更匹配的原子,提升了算法的重建性能。
基于广义Jaccard系数的SWOMP算法步骤如下。
输入:
输出:重建信号
1) 初始化:r0=y;Λ0=Ø;A0=Ø;s=1;
2) 计算u=abs[Jaccard(AT,rs-1)];
其中, 选择u中大于门限Th的值,Th=αmax{abs(u)},将这些值对应的A的序列号记为J0;
3) 令Λs=Λs-1∪J0,As=As-1∪aj,若Λs=Λs-1, 则迭代停止, 进入7);
4) 求最小二乘解:
5) 更新残差:rs=y-As
6) 如果s≤m, 则令s=s+1,返回2)继续迭代,如果s > m或rs=0,则停止迭代,进入7);
7) 输出重建信号的近似值
其中:J0表示每次迭代找到的索引;Λs表示s次迭代索引集合;aj表示矩阵A的第j列;As表示由索引集Λs选出的矩阵A的列集合;rs-1表示残差;〈a,b〉表示求a和b的内积;s表示迭代次数。
3 实验结果及分析语音信号是非平稳的时变信号,但在10~30 ms内可近似认为是平稳的,也就是语音信号具有短时平稳性。因此,在对语音信号重建时,首先对输入的语音信号进行分帧处理,得到时长为10~30 ms的多帧信号,然后对每帧语音信号使用离散余弦基进行稀疏表示,再经过观测矩阵进行观测,最后在重建端应用重建算法完成对语音信号的重建。
仿真实验所用语音信号来自于中科院自动化研究所CASIA语音库的男、女声语音信号,时长为1~3 s,频率为16 kHz。实验的帧长取320个采样点(20 ms)。实验均在Intel(i5-4 200 M,4 GB内存)平台上完成,仿真软件为Matlab2017a。
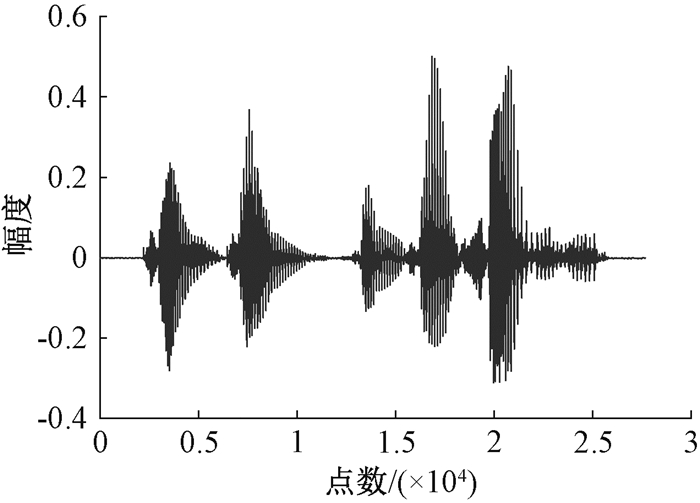
信号具有稀疏性是压缩感知理论应用的前提条件,为了验证语音信号具有稀疏性,实验选取男声语音中一段内容为“竞争增加效益”的信号,将其在DCT域下进行稀疏表示,图 1为原始时域波形图,图 2为DCT域图。
|
图 1 原始语音时域图 Fig. 1 Time domain diagram of original speech |
|
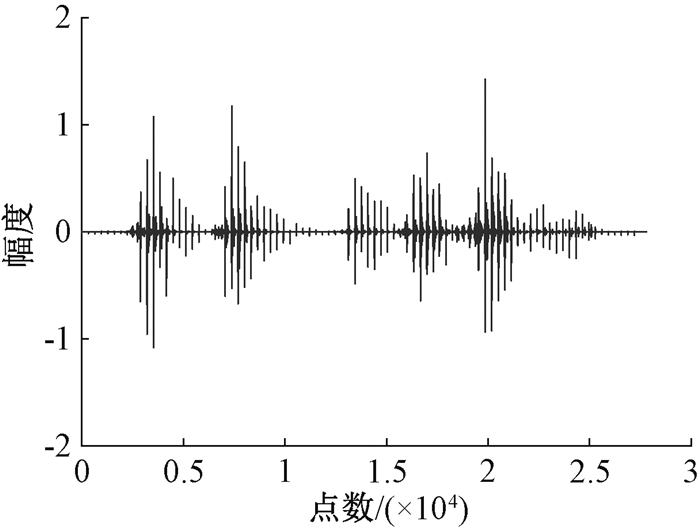
图 2 原始语音DCT域图 Fig. 2 The original voice DCT domain diagram |
通过图 1和图 2对比可知,原始语音信号在DCT域中仅存在少数较大值,其余值都很小,甚至为零,故语音信号在DCT域是稀疏的,满足压缩感知理论应用前提。
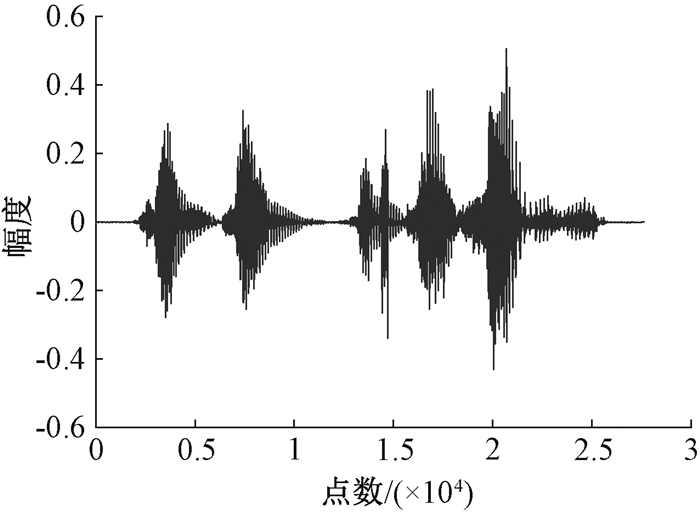
3.1 主观分析稀疏基采用DCT基,观测矩阵采用随机高斯矩阵,压缩比(M/N)为0.5,应用SWOMP算法和基于广义Jaccard系数的SWOMP算法对男声语音中一段内容为“竞争增加效益”的语音进行重建,重建的时域结果如图 3、4所示。
|
图 3 SWOMP算法重建语音信号的时域结果图 Fig. 3 Time domain result of reconstruction of speech signal by SWOMP algorithm |
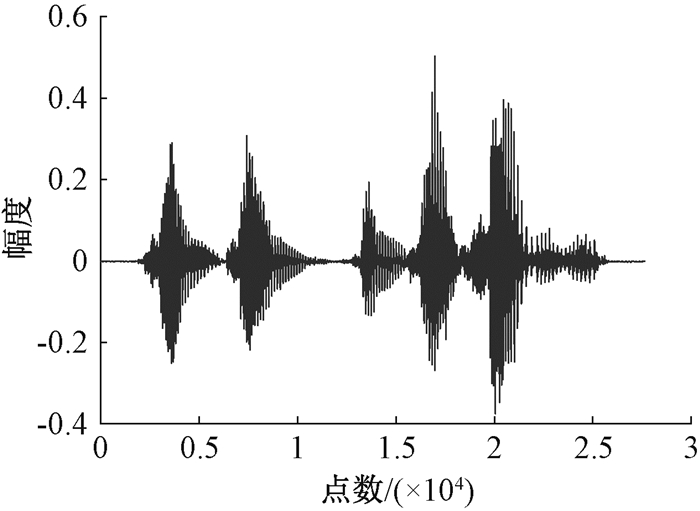
|
图 4 基于广义Jaccard系数的SWOMP算法重建语音信号的时域结果图 Fig. 4 Time domain result of speech signal reconstruction based on SWOMP algorithm based on generalized Jaccard coefficients |
对比图 1、图 3和图 4可知,相较于SWOMP算法,基于广义Jaccard系数的SWOMP算法重建语音信号的时域图更接近原始语音信号的时域图,重建效果更好。
3.2 客观分析为了客观评价基于广义Jaccard系数的SWOMP算法对语音信号的重建性能,本文采用平均帧信噪比(average frame signal noise rate, AFSNR)和客观语音质量评估(perceptual evaluation of speech quality,PESQ)两种客观评价指标比较重建语音信号的质量。单位均帧信噪比rAFSNR计算为
| $ r_{\mathrm{AFSNR}}=\frac{1}{P} \sum\limits_{k=1}^{P} 10 \log 10\left\{\frac{\left\|u_{k}\right\|_{2}^{2}}{\left\|u_{k}-\hat{u}_{k}\right\|_{2}^{2}}\right\},$ | (11) |
其中:uk表示第k帧语音信号;
PESQ得分在2001年被国际电讯联盟(ITU)采纳为一种语音信号评价指标,分值为-0.5~4.5分,分值越高越好。本文实验的PESQ得分是由PESQ程序对比原始语音与重建语音所得出。
以离散DCT基作为稀疏基,观测矩阵采用随机高斯观测矩阵,压缩比为0.1~0.6,对比以内积准则度量原子和残差的相关度的SWOMP算法和基于广义Jaccard系数的SWOMP算法为重建算法,实验分别选取1位男生和1位女生,每人选取50句语音信号进行重建,为简化表格,基于广义Jaccard系数的SWOMP算法以J-SWOMP算法表示,重建信号的AFSNR值如表 1所示,PESQ得分的平均值如表 2所示。
|
|
表 1 不同语音重建的AFSNR值 Tab. 1 AFSNR values of different speech reconstructions |
|
|
表 2 不同语音重建的PESQ得分 Tab. 2 Average PESQ scores of different speech reconstructions |
由表 1可知,随着压缩比的增大,两种算法重建语音信号的AFSNR值也随之增大,在压缩比一定时,J-SWOMP算法重建信号的AFSNR值始终大于SWOMP算法。当压缩比为0.1~0.6时,J-SWOMP算法比SWOMP算法重建男声信号的AFSNR值平均提高了2.869 3 dB;女声信号的AFSNR值平均提高了2.457 8 dB。
由表 2可知,在压缩比为0.1~0.6时,J-SWOMP算法与SWOMP算法相比对男声重建信号的PESQ平均得分提高0.605 4;对女声重建信号则提高了0.550 2。
取上述实验所用的50句短语中,内容为“国家改革企业”的男声和女声语音信号进行重建,实验重复100次,实验得到的AFSNR值如表 3所示,PESQ得分如表 4所示。
|
|
表 3 不同算法的重建语音信号的AFSNR值 Tab. 3 AFSNR values of reconstructed speech signal of different algorithms |
|
|
表 4 不同算法的重建语音信号的PESQ值 Tab. 4 PESQ values of reconstructed speech signal of different algorithms |
由表 3可知,内容为“国家改革企业”的语音信号、压缩比为0.1~0.6时,J-SWOMP算法与SWOMP算法相比,男声信号AFSNR值平均提高了2.329 7 dB;女声信号提高了2.612 1 dB。对于内容为“竞争增加效益”的语音信号,在压缩比为0.1~0.6时,J-SWOMP算法比SWOMP算法的男声的AFSNR值平均提高了2.104 3 dB;女声平均提高了2.415 2 dB。
对内容不同的语音信号进行分析,随着压缩比的增大,两种算法重建语音信号的PESQ得分也随之增大,在压缩比一定时,J-SWOMP算法重建语音信号的PESQ得分大于SWOMP算法。由表 4可知,当压缩比为0.1~0.6时,内容为“国家改革企业”语音信号,J-SWOMP算法比SWOMP算法的男声PESQ平均得分提高了0.457 2,女声平均提高了0.625 6;内容为“竞争增加效益”语音信号,J-SWOMP算法比SWOMP算法的男声PESQ平均得分提高了0.412 3;女声平均提高了0.451 3。
4 结论本文利用广义Jaccard系数匹配准则替代内积匹配准则实现最佳匹配原子的筛选,提出了基于广义Jaccard系数的SWOMP算法,该算法能通过挑选出和语音信号残差更匹配的原子,解决了SWOMP算法中原子丢失的不足,提高了语音信号重建的质量。通过仿真实验可知:在相同条件下,基于广义Jaccard系数的SWOMP算法对语音信号重建的AFSNR值和PESQ得分要明显高于SWOMP算法。
| [1] |
周健, 刘荣敏, 窦云峰, 等. 采用L1/2稀疏约束的梅尔倒谱系数语音重建方法[J]. 声学学报, 2018, 43(6): 991-999. ZHOU J, LIU R M, DOU Y F, et al. Speech reconstruction from Mel-frequency cepstral coefficients via L1/2 sparse constraint[J]. Acta acustica, 2018, 43(6): 991-999. (  0) 0) |
| [2] |
DONOHO D L. Compressed sensing[J]. IEEE transactions on information theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 (  0) 0) |
| [3] |
CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE transactions on information theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 (  0) 0) |
| [4] |
隋昊, 周萍, 沈昊, 等. 基于混沌序列的压缩感知语音增强算法[J]. 微电子学与计算机, 2018, 35(1): 96-99, 105. SUI H, ZHOU P, SHEN H, et al. Compressed sensing speech enhancement algorithm based on chaotic sequences[J]. Microelectronics & computer, 2018, 35(1): 96-99, 105. (  0) 0) |
| [5] |
赵辉, 张静, 张乐, 等. 基于非局部低秩和加权全变分的图像压缩感知重构算法[J]. 电子与信息学报, 2019, 41(8): 2025-2032. ZHAO H, ZHANG J, ZHANG L, et al. Compressed sensing image restoration based on non-local low rank and weighted total variation[J]. Journal of electronics & information technology, 2019, 41(8): 2025-2032. (  0) 0) |
| [6] |
邓垚, 李登峰. 分块筛选自适应压缩感知重构算法[J]. 计算机应用与软件, 2020, 37(5): 233-237, 274. DENG Y, LI D F. Self-adapting compressed sensing reconstruction algorithm based on partitioned filtering[J]. Computer applications and software, 2020, 37(5): 233-237, 274. DOI:10.3969/j.issn.1000-386x.2020.05.040 (  0) 0) |
| [7] |
杨真真, 杨震. 语音压缩感知硬阈值梯度追踪重构算法[J]. 信号处理, 2014, 30(4): 390-398. YANG Z Z, YANG Z. Hard threshold gradient pursuit reconstruction algorithm for speech compressed sensing[J]. Journal of signal processing, 2014, 30(4): 390-398. DOI:10.3969/j.issn.1003-0530.2014.04.004 (  0) 0) |
| [8] |
BLUMENSATH T, DAVIES M E. Stagewise weak gradient pursuits[J]. IEEE transactions on signal processing, 2009, 57(11): 4333-4346. DOI:10.1109/TSP.2009.2025088 (  0) 0) |
| [9] |
张宇, 刘雨东, 计钊. 向量相似度测度方法[J]. 声学技术, 2009, 28(4): 532-536. ZHANG Y, LIU Y D, JI Z. Vector similarity measurement method[J]. Technical acoustics, 2009, 28(4): 532-536. DOI:10.3969/j.issn1000-3630.2009.04.021 (  0) 0) |
| [10] |
王顶, 吴玥瑶, 曹旺辉, 等. 基于Dice匹配的SWOMP压缩感知重构算法[J]. 西北工业大学学报, 2017, 35(5): 774-779. WANG D, WU Y Y, CAO W H, et al. Improved reconstruction algorithm for compressed sensing[J]. Journal of northwestern polytechnical university, 2017, 35(5): 774-779. DOI:10.3969/j.issn.1000-2758.2017.05.005 (  0) 0) |
| [11] |
TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE transactions on information theory, 2007, 53(12): 4655-4666. DOI:10.1109/TIT.2007.909108 (  0) 0) |
| [12] |
NEEDELL D, VERSHYNIN R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J]. IEEE journal of selected topics in signal processing, 2010, 4(2): 310-316. DOI:10.1109/JSTSP.2010.2042412 (  0) 0) |
| [13] |
于春肖, 杨艳芳, 井丁卉. 不完全正交的变参数H-IGMRES(m)算法[J]. 郑州大学学报(理学版), 2020, 52(1): 93-98. YU C X, YANG Y F, JING D H. Incompletely orthogonal variable restart parameter H-IGMRES(m) algorithm[J]. Journal of Zhengzhou university(natural science edition), 2020, 52(1): 93-98. (  0) 0) |
 2022, Vol. 54
2022, Vol. 54

