2. 可信计算北京市重点实验室 北京 100124
2. Beijing Key Laboratory of Trusted Computing, Beijing 100124, China
在区块链中,每个节点都是独立的,具有自治性。不同的节点维护着内容相同的区块链账本,同时也各自独立地将网络中产生的新的交易打包成一个区块,并广播给其他节点。区块链是线性的,所以同一时期只有一个新打包的区块能加入主链,以保证数据的一致性,因此,如何选择区块是区块链共识的重要任务之一。这个过程又称为如何分配记账权[1]。
基于算力的共识算法存在许多弱点,包括弱一致性、低交易吞吐量和一些共识攻击,比如51%攻击(可以导致双重攻击[2-3], 私自挖矿[4-5]),它意味着当算力达到51%这个阈值时,这种攻击几乎可以成功。
现有的基于算力,即工作量证明的区块链系统都依赖于这样的假设:攻击者不能拥有超过33%或者51%的算力,然而随着比特币攻击的复杂性,这个假设有可能不再成立。以SHA256哈希算法为例,产生这个算法的哈希碰撞需要248年,但是随着量子计算机技术的发展,此哈希算法有可能会在有限时间内被破解[6]。基于算力的共识算法在安全性和性能方面已经有了一些改进。有一种利用基于历史行为的信任值来代替算力的共识算法的机制[7-8],此机制可以根据历史行为检测恶意节点,降低恶意节点争夺记账权的成功率。此机制只是对特定的行为(比如身为领导者却没有在规定时间内打包新区块)进行监测,以此来决定每个节点的信任值,但由于简单,不适用于复杂的应用场景。文献[9]提出的Byzcoin共识算法建立在Bitcoin-NG和实用拜占庭容错算法(practical Byzantine fault tolerance, PBFT)的基础上。在Byzcoin算法中,经过挖掘找到密钥块的节点在有限时间内会成为见证人,每次创造一个新的密钥块时,都会通过一组见证人之间的PBFT视图变更协议选出新的领导者。新领导者每隔几秒就会提交一个包含新交易的区块。如果一组见证人已经通过验证并同意微块,则领导者提交微块。协议本质上是一个两阶段的PBFT协议,通过集体签名的方案取代了MAC(media access control)认证。通过这种方式,每次创建新的密钥块时,证人组基于其计算能力动态地形成新的领导者,并且每隔几秒就可以提交一个包含一组事物、并且有足够数量证人集体签字的微块。当领导者是恶意的并且不产生微块,虽然Byzcoin可以检测到它,但是却没有其他惩罚,不能阻止其再次成为领导者。所以,Byzcoin遭受共识攻击的成本是相同的。
本文在现有的基于算力的共识机制的基础上,提出了一种基于可信性评估的区块链共识机制,并提出了一种节点信任值评估算法,经过性能测试和安全性分析,表明本文的共识机制对于基于算力的攻击成本远超过现有的共识算法。
1 基于可信性评估的区块链共识机制共识机制的工作流程为:通过对节点区块链的可信性进行评估得到每个节点的信任值,根据信任值随机动态选出共识组,经过工作证明共识挖掘到的密钥块决定共识组中成为此轮的领导者的成员,领导者发布包含交易的微块,共识组通过改进多重签名共识算法与领导者达成共识。
为了抵御基于算力的攻击,本机制采用信任值代替算力进行记账权的争夺。首先按照信任值排名,当信任值达到一定的阈值,才可能被随机选中进入共识组。用信任值代替算力,这样保证了一个节点的投票能力是取决于它的综合表现,而不是某一瞬间的计算能力,而它的综合表现需要长时间有规律的工作。只有诚实的节点,表现正常并且有规律,才可能成为共识组的一员。所以,即使算力很高的节点,如果进入系统不久也无法攻击系统。共识组中会有一节点被随机选中成为领导者,领导者可以产生微块对交易进行打包,其他节点对微块进行共识,此轮工作结束,开始下一轮领导者的选举。
本机制中区块链由一个个大块串联而成,其中每个大块由两种区块组成,密钥块和微块。其中大块中密钥块的数量和微块数量都是固定和提前预设的。大块即区块链中的区块,它包含了固定个数的密钥块和微块。只是它不包含随机数,任何人都可以产生大块。密钥块用于确定领导人。一个秘钥块由5个域构成:前一个密钥块的散列值;随机数;节点的公钥;产生这个密钥块的节点的信任值;该块的散列值。共识组组员通过检查该块的散列值的有效性验证密钥块。微块是一个简单的块,每隔几秒就会验证一次,包括验证历史交易。为了防止双重支出,每个微块在被接受之前都要被提议给共识组,如果微块被验证成功,则会成为区块链的一部分。微块由5个域构成:当前与其对应的密钥块的散列值;前一个固定在区块链中的微块的哈希值;一组Merkle树的交易;前三者的散列值;来自共识的签名。为了验证微块的有效性,共识组成员检查Msig的有效性,验证密钥块和前面的微块的散列值,并验证交易TXs。
2 信任值评估算法 2.1 信任值设计原则通过信任值计算,想要成为领导者不仅要创建足够的密钥块,还要表明其诚实有规律地工作,每个节点通过区块链维护自己的信任值副本。用R来表示信任值,R∈[0, 1]。信任值在每一轮开始时,即新的密钥块被创建时,都会被更新。信任值的计算要符合社会对系统的3个要求:1)初期的增长要缓慢;2)进入一段时间后,通过快速增长信任值,鼓励它参与共识;3)后期要缓慢增加防止垄断现象。
信任值通过节点对系统的工作量和工作的规律性进行计算。通过信任值机制,除了创建足够的近期密钥块之外,节点还必须表明它已经诚实地工作一段时间了。本文中的信任评估算法包括内部评估和外部评估;内部评估表示对节点的历史行为表现进行评估,主要从贡献率和工作规律性进行评估;外部评估则从与其进行历史交易的节点进行评估。
2.2 内部信任值计算内部信任值主要表现为节点对区块链的贡献率和工作的规律性。贡献率可以用其生产的密钥块的个数决定,规律性可用其作为领导者所产生的微块数量决定。信任值的算法如下。
输入:L, 本轮生产的所有密钥块k, 微块m, c, a, λ
输出:节点的信任值R,R∈[0, 1]。
1)
2)
3)
4)
5) y1=meank/(1+sm)。
6) if Nl≥1 then y2=meanm/(1+sk)。
7) else y2=1。
8) end if。
9) x=y1y2 L。
10)
上述算法中符号L代表当前区块链的长度;c代表大块的大小,大块中包含系统预先定义数量的密钥块;t代表区块链中包含的大块数量;Ki代表在第i个大块中节点创造的密钥块数量;Nl代表节点被选为领导者的次数;mj代表在第j轮节点所生产的微块被验证成功的数量;m代表一个领导者被预定的生成的微块数;meani代表由一个节点或一个领导者在区块链中创建的密钥块(如果i为k)或微块(如果i为m)的平均值;Si对应平均值的标准差;(a,λ)为系统参数。
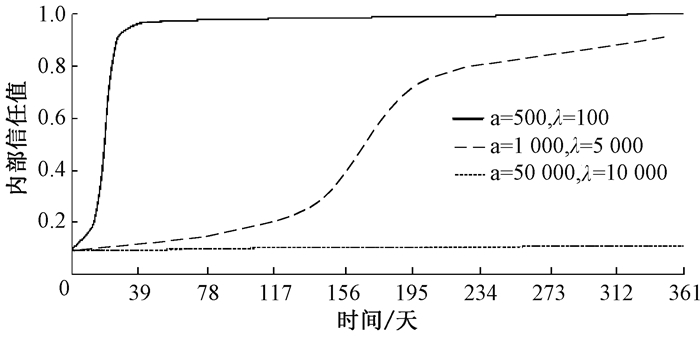
f(x)是一个sigmoid函数。它确保节点一开始只能慢慢增加信任值,即使拥有强大的计算能力,一个节点需要经过一段时间的工作,逐步将其信任值提升到转折点,到达转折点的节点可以证明它足以被信任,信任值增长变快。最后,随着信任值增加,信任曲线趋于稳定,有利于促进节点之间的权力平衡。信任值函数也有一些参数,参数(a,λ)可以用来调节信任值变化的快慢。f(x)的斜率与λ的值直接相关。
因此,节点的综合能力是由节点在其活动期间完成的有效工作总量, 以及整个区块链中该工作的规律性给出的,而不是节点在给定时间的采矿能力。所以,当系统运行一段时间后,即使是具有强大计算能力的节点也无法迅速建立其信任值,它需要诚实而有规律地为系统做出贡献,以获得信任值。
2.3 外部信任值计算本文从信任的主观性与不确定性入手提出了外部信任值的计算方法,引入b、d、u 3个变量来描述节点的信任关系,这些变量由交易产生的评价计算所得:b表示对目标节点的信任度;d表示对目标节点不信任度;u表示不确定目标节点的信任程度。3个变量满足公式b+d+u=1, {b, d, u}∈[0, 1]。
在现在研究中不确定因子wc被设置为常数,忽略了网络环境中的不确定因素。本文中设置不确定因子wc与实体间的交互事件相关,计算方法为wc=E-(r+s);b、d、u的计算公式为b=r/(r+ps+wc);d=ps/(r+ps+wc);u=wc/(r+ps+wc), 其中p表示对节点否定事件的惩罚因子,取值大于1。实体的否定行为能够增大信任观念空间中的不信任程度,从而实现了对实体否定行为的惩罚机制。基于上述表示信任关系的三元组,共识组对节点的外部信任计算公式为
| $ Ext = b + u/2 = \left( {r + E - s} \right)/2\left( {ps + E - s} \right), $ | (1) |
其中:Ext为外部信任值,由与其进行历史交互的节点对其进行信任评价。在本文中,我们定义外部信任值落在[0, 1]区间。信任值为1表示目标节点完全信任;为0.5则表示无法判断目标节点的可信度;为0则表示目标节点不可信。我们把默认外部信任值设为0.5。r表示关于目标节点的肯定事件数;s表示否定事件数;E为节点的交易数。
从式(1)可以看出,外部信任值随着肯定事件r的增大而增大,随着否定事件s的减小而减小。而且如果p的取值增大,则外部信任值会减小。因此,最终的信任值R的表达式为R=min(1, f(x)+γ(Ext-0.5)),如果R值为负数,则直接取0,其中γ为内部和外部信任值所占的比例。
3 评估 3.1 性能评估共识延迟表示交易在构建完成到上链的时间。上链意味着交易被各个节点接受、确认。因为本算法每轮只有一位领导者产生,并且每轮发布的微块数量固定,所以本共识算法不会产生分叉,每笔交易达到共识要求即被认为可以上链。该时间是衡量共识算法的重要性能指标,用TTXreach表示,TTXreach=TTXBroadcast+TConsensus,其中:TTXBroadcast表示共识从创建到被共识组的成员接收的时间;TConsensus表示共识组的成员与领导者达成共识的时间。
为了达成共识,要求至少一半成员就价值达成一致。我们使用大小为1 KB的密钥块和大小为512 KB、1 MB、2 MB和4 MB的微块进行实验。与微块不同,密钥块通常很小,因为它们不包含任何交易。图 1表明共识延迟随着块大小而显著增加。这种趋势背后的原因有两点:领导者向共识组提出微块需要更长的时间;计算较大块的哈希值并验证其包含的交易会消耗更多时间。此外,本共识机制中,当组大小从4增加到16时,共识延迟增加超过50%。虽然延迟增加,但即使在考虑大小为4 MB的块时,也可以在约0.5~1.2秒内达到共识。而以太坊需要15秒的出块时间,比特币需要10分钟出块时间。基于分叉考虑,它们还需要后续多个区块上链之后才能确认区块真正被上链,因此以太坊和区块链的交易时间远远高于本共识机制。
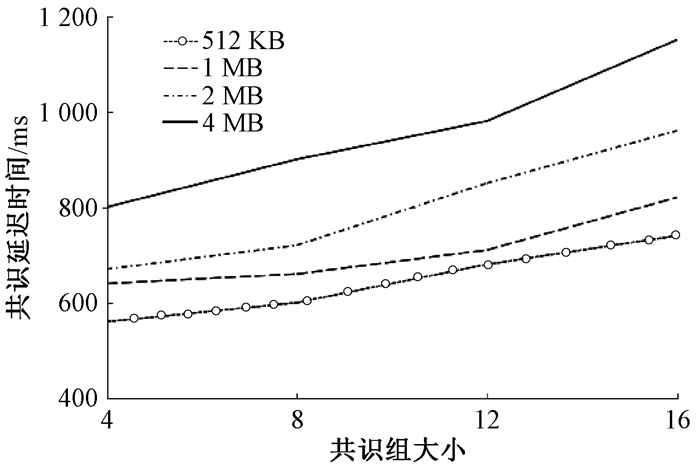
|
图 1 共识延迟时间 Fig. 1 Delay time of consensus |
吞吐量是衡量共识算法处理交易效率的重要指标。吞吐量表示每秒处理的交易数量,是交易被创建到确认上链的区块链的交易数量与此轮时间的比,计算公式为TPSΔt=(TtotalTXΔt)/Δt,其中:Δt表示一轮共识所用时间,即从一位领导者到下一位领导者选举所耗费的时间;TotalTXΔt表示该时间上链的微块包含的交易数量。由图 2可见,微块和共识组的大小直接影响吞吐量。共识组越小,吞吐量越高,达成共识的难度和时间都会减少,上链的区块越多,吞吐量越高。
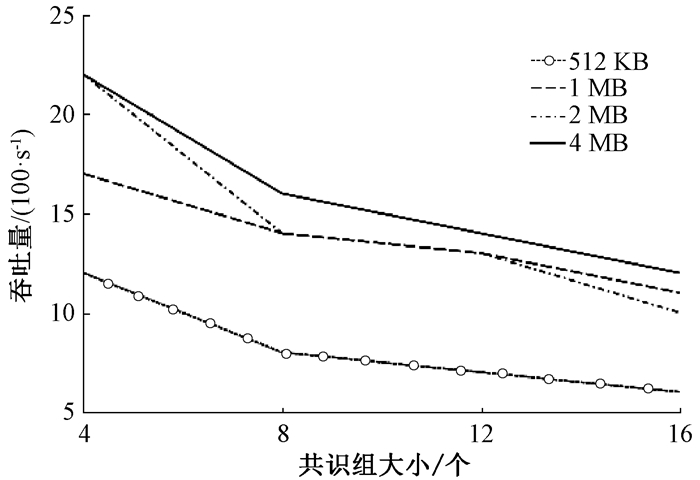
|
图 2 吞吐量 Fig. 2 Throughput |
1) 外部信任值分析。首先可以固定外部信任值计算方法中wc和E,即确认肯定事件r与否定事件s的和,然后依次随机增加肯定事件r和否定事件s到指定数量,并且使不信任程度d增大。图 3为所选的节点随着不信任程度d的增加,信任值的变化情况。由3.1节的吞吐量测试可知,当微块大小为4 MB、共识组成员为4时,本共识机制吞吐量可以到达2 000 TPS, 我们可以设E=20 000,wc=5 000,随着r与s的增长,重复试验次数100次,信任值变化如图 3所示。
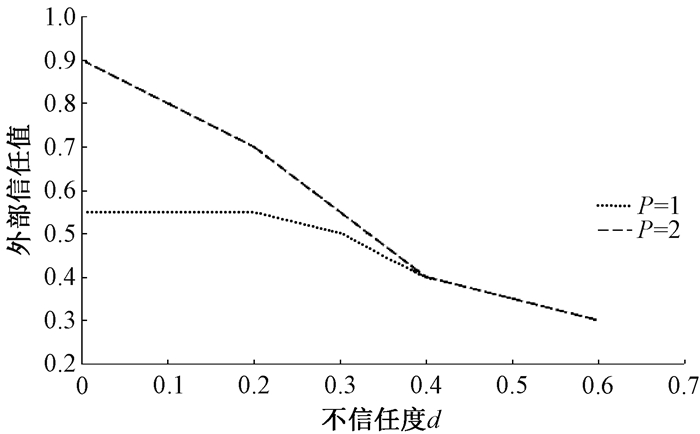
|
图 3 惩罚因子分析 Fig. 3 Penalty factor analysis |
外部信任值通过控制惩罚因子P来调节对恶意行为的惩罚程度。在相同的网络环境中,设置P分别为1、2,观察不同参数对信任值的影响。由图 3可知,P值越大,惩罚程度越大,信任值下降越快。随着否定事件r的增加,不信任程度d也会增加,P=2时,外部信任值由0.9降到0.3,而P=1时,惩罚力度较小,外部信任值由0.5降到0.4。
2) 内部信任值分析。本实验使用比特币采矿网络中的前11个采矿池来模拟本系统中的节点算力分布,前11个采矿池的总计算能力约为85.74%。如图 4所示为最近一年内算力值最大的矿池BTC的内部信任值变化曲线。内部信任值可由公式(1+(x-a)/λ+|x-a|)/2计算得到,其中:x表示算力在内的综合能力;a、λ可以控制信任值变化快慢。由图 5可知,随着参数a、λ的增大,信任值变化也会变快。
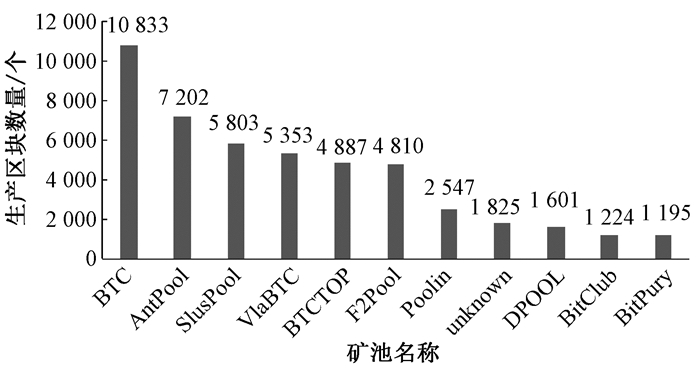
|
图 4 比特币算力分布 Fig. 4 Bitcoin power distribution |
|
图 5 内部信任值变化 Fig. 5 Change of interior trust value |
3) 综合信任值分析。信任值由内部值和外部值计算得到,内部信任值和外部信任值的变化快慢不一样,需要权值进行平衡,权值为γ。
内、外部信任值在不同时间的增长速度不一样,设Rnew为目前为止所有节点中最大的信任值,Tsecond表示系统运行的时间,c为信任值变化调节因子。则权值为γ=c·Rnew/Tsecond,这样可以降低外部信任值的变化率,使之趋向于内部变化率。
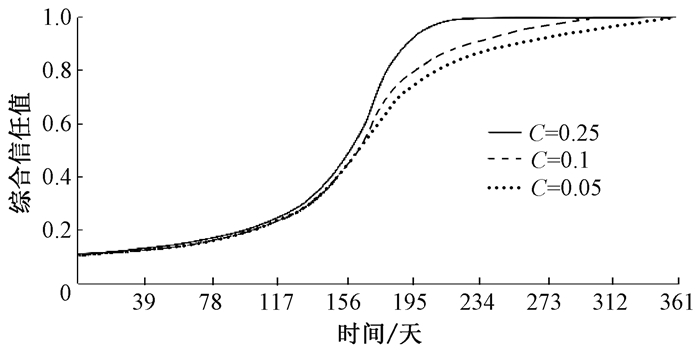
图 6为最近一年内,算力值最大的矿池BTC的综合信任值变化曲线。每个矿池的信任值都会随着时间增加而增加。
|
图 6 综合信任值变化 Fig. 6 Change of comprehensive trust value |
设P=2、c=0.05、a=5 000、λ=1 000进行实验,结果表明前3个月所有节点的信任值在(0, 0.2]的范围内;第5个月时,64.5%的节点的信任值在(0, 0.2]的范围内,35.5%的节点进入到(0.2, 0.4]范围内;第6个月时,20.6%的节点的信任值在(0, 0.2]的范围内,59.2%的节点进入到(0.2, 0.4]范围内,20.2%的节点的信任值进入到(0.4, 0.6]的范围内; 到第7个月的时候,15.2%的节点的信任值进入到(0.6, 0.8]范围内;到1年后,才有16.4%的节点的信任值进入到(0.8, 1]的范围内。
从实验结果可以看出声誉值是在时间的基础上,基于节点的表现动态变化的,就算是算力强大的节点,也需要超过1年才能达到高于0.8的信任值,抵御了贿赂攻击。因此,当在系统刚刚建立阶段,每个节点信任值都不高,是系统比较脆弱的时候,信任值达到共识组的阈值时间较短。如果恶意节点在系统建立初期潜伏到系统中,只需要简单的努力就可使自己的信任值排到前N%;但是当系统达到稳定状态后再加入系统,则需要相当长的时间来建立自己的信任值,攻破系统的难度也会增加。
3.3 攻击成本分析攻击成本为攻击成功所需要的时间、算力的乘积。攻击成功为共识组有半数成员为恶意节点。
在选取共识组成员时,前N%的成员进入候选组,然后从候选组随机挑选成员进入共识组,当共识组成员的分数之和与全体成员的分数之和大于Z%时,完成共识组成员的选取。随着N%和Z%的增长,攻击成本也会越来越大。我们分析当N%取20%、Z%取30%时的情况,攻击成本不仅与算力、还与节点加入系统的时间、系统已经运行的时间相关。我们假设α为整个网络算力的基本单位,g为维持1个算力单位一小时所需要的价钱,所以αg为所需要的攻击成本。
为了成功攻击比特币,在最好的情况下,攻击者需要51%的算力,并且需要6个区块确认时间,大约为1小时来延续自己的私链。那么比特币的攻击成本为0.51 αg。重复此攻击的成本是相同的。对于ByzCoin,在最好的情况下,攻击者需要34%的算力,以及整个窗口(1 008个区块)维持大约一周的时间。因此,攻击成本为168*0.34 αg,约为57.12 αg。在N%=20%时,排名在前20%的节点信任值最低为Rtarget,一个节点只有超过此阈值才有机会入选共识组参与共识,所以,攻击成功的前提是要使恶意节点的值超过Rtarget。在系统运行的不同时刻,Rtarget的值不同。
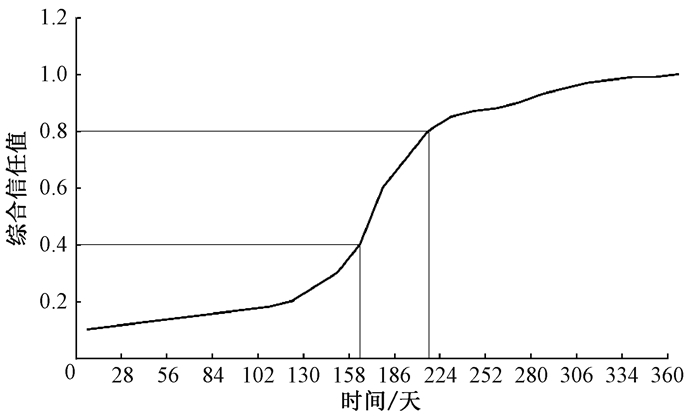
图 7为算力占全网20%的节点的信任值随着时间的变化情况:如果Rtarget=0.4,则节点需要工作158天才有可能进入共识组。攻击成本为0.2 α*(150*24 g)=720 αg;如果Rtarget=0.8,则节点需要工作210天,才有机会进入共识组。攻击成本为0.2 α*(210*24 g)=1 008 αg。
|
图 7 综合信任值变化图 Fig. 7 Change of comprehensive trust value |
本文提出的共识机制明显优于比特币和ByzCoin,由图 7也可以看出,随着时间的增加,攻击者所付出的成本逐渐增大,且一定时间后,攻击成本高于收益,因此保障了系统的安全性。
共识机制的思想:首先,信任值是基于节点的历史表现生成的,只有通过投入大量的算力和时间成本来获得足够的信任值,才有可能拥有决策权。这与以往的系统不同,以往系统只通过一瞬间的算力值来决定其是否拥有决策权,这样避免了51%算力攻击;其次,以往系统没有记忆功能,对攻击者的惩罚太小,本文引入惩罚因子,对攻击者进行惩罚,从而避免了重复攻击。
4 结语本文对现有的基于算力的共识机制的不足进行了分析,提出了一种基于可信性评估的区块链共识机制,并提出了一种节点信任值评估算法。每个节点信任值由内部信任值和外部信任值综合得到,能够更好地表征节点的工作表现。通过对共识机制进行测试,表明本文设计的共识机制的攻击成本是比特币的几百倍,是ByzCoin的几十倍,而且也能防御基于算力的攻击。本文的共识机制在吞吐量和共识延迟方面均有较好的表现。
| [1] |
段希楠, 延志伟, 耿光刚, 等. 区块链共识算法研究与趋势分析[J]. 科研信息化技术与应用, 2017, 8(6): 43-51. DUAN X N, YAN Z W, GENG G G, et al. Research and trend analysis on blockchain consensus algorithm[J]. E-science technology and application, 2017, 8(6): 43-51. (  0) 0) |
| [2] |
APOSTOLAKI M, ZOHAR A, VANBEVER L. Hijacking bitcoin: routing attacks on cryptocurrencies[EB/OL].(2016-03-24)[2019-02-10]. https://arxiv.org/abs/1605.07524.
(  0) 0) |
| [3] |
KARAME G O, ANDROULAKI E, CAPKUN S. Double-spending fast payments in bitcoin[C]//Proceedings of the 2012 ACM Conference on Computer and Communications Security. Raleigh, 2012: 906-917.
(  0) 0) |
| [4] |
EYAL I, SIRER E G. Majority is not enough: bitcoin mining is vulnerable[C]//International Conference on Financial Cryptography and Data Security. Berlin, 2014: 436-454.
(  0) 0) |
| [5] |
NAYAK K, KUMAR S, MILLER A, et al. Stubborn mining: generalizing selfish mining and combining with an eclipse attack[C]//2016 IEEE European Symposium on Security and Privacy (EuroS & P).Saarbrucken, 2016: 305-320.
(  0) 0) |
| [6] |
GILBERT H, HANDSCHUH H. Security analysis of SHA-256 and sisters[M]. Berlin: Springer, 2004: 175-193.
(  0) 0) |
| [7] |
张永, 李晓辉. 一种改进的区块链共识机制的研究与实现[J]. 电子设计工程, 2018, 26(1): 38-42, 47. ZHANG Y, LI X H. The research and implementation of an improved blockchain's consensus mechanism[J]. Electronic design engineering, 2018, 26(1): 38-42, 47. DOI:10.3969/j.issn.1674-6236.2018.01.008 (  0) 0) |
| [8] |
徐治理, 封化民, 刘飚. 一种基于信用的改进PBFT高效共识机制[J]. 计算机应用研究, 2019, 36(9): 2788-2791. XU Z L, FENG H M, LIU B. Improved PBFT efficient consensus mechanism based on credit[J]. Application research of computers, 2019, 36(9): 2788-2791. (  0) 0) |
| [9] |
EYAL I, GENCER A E, SIRER E G, et al. Bitcoin-NG: a scalable blockchain protocol[C]//Proceedings of the 13th Usenix Conference on Networked Systems Design and Implementation.Santa Clara, 2016: 45-59.
(  0) 0) |
 2020, Vol. 52
2020, Vol. 52

