随着世界经济全球化与科学技术的快速发展,第三方支付服务成为人们生活的一部分,比如支付宝和微信支付在中国随处可见,数不胜数的交易发生在世界各地的在线交易平台上,随之而来的欺诈犯罪问题也更加严重,然而数据的不平衡问题是影响欺诈检测的难点。为了解决不均衡数据的分类问题,学者们的研究方法主要可以分为:对原始数据进行数据处理, 对算法模型进行优化改进[1]。
数据处理主要是指根据统计学原理和其他方法对样本集进行扩充或者剔除操作,达到将样本集从类别不均衡分布到均衡分布的转变。这方面最具代表性的方法就是重采样方法,主要可分为上采样方法和下采样方法。其中经典的有SMOTE算法[2]以及基于SMOTE算法衍生的改进型算法。也有学者结合上采样和下采样两种方法的混合采样算法处理样本集[3]。杨毅等设计了一种精化Borderline-SMOTE方法解决数据不平衡问题[4],该方法通过对小类样本的边界样本重复采样从而改善原始样本集的类别分布。石洪波等详细阐述了SMOTE算法的原理以及存在的问题[5], 针对SMOTE存在的问题, 分别介绍了4种扩展方法和3种应用的相关研究。蒋华等在SMOTE算法和ADASYN算法的基础上设计了一种采样方法[6],该方法根据K近邻算法计算小类样本点和大类样本点数目, 对小样本点进行分类后分别采用ADASYN和SMOTE算法进行小类样本点合成。
算法改进角度是指基于传统的分类算法和原始数据集的不平衡分布特点,对分类算法本身进行有针对性的改进优化,常见的方式有加入惩罚因子和将多个弱分类结果进行结合等。改进算法有对集成学习算法的改进[7]、对传统的二分类算法和对数概率回归算法的改进、对基于代价敏感算法的改进[8]等。王忠震等在欠采样和代价敏感的基础上设计了针对不平衡数据的分类算法(USCBoost)[9],该算法首先在AdaBoost迭代前对大类数据权重排序,并根据排序选择大类数据与小类数据合并临时数据训练基分类器。
近些年来生成对抗网络(generative adversarial networks, GAN)[10]非常热门,在图像生成[11]和图像增强[12]等领域应用中获得了巨大的成功,由于GAN设计的原因,梯度的修正需要生成器的输出是一个连续空间,所以GAN很少用于离散空间的数据增强。文献[13]提出了一种基于条件Wasserstein-GAN的过采样方法,该方法能有效地对含有数值和分类变量的表格数据集进行建模,并通过辅助分类损失特别关注下游分类任务。
目前,学者们解决样本类别不均衡问题以重采样技术为主,针对GAN应用与交易欺诈方面的研究较少,而且采样过程过度依赖原始数据集,因此本文提出了一种基于特征优化生成对抗网络的在线交易反欺诈方法。本文主要贡献:1) 设计一种基于特征优化生成对抗网络的在线交易反欺诈方法,解决传统采样方法过度依赖原始数据的问题;2) 提出了KGC-WGAN模型,该模型针对交易数据提取Key特征加入到生成器中优化生成数据质量和提高训练稳定性,将Gumbel-softmax应用到网络中解决类别数据生成过程中梯度消失的问题,解决交易欺诈数据的生成问题;3) 从原始数据规模、重采样方法、分类方法和采样比例等方面进行了对比,实验结果证明了本文方法的有效性。
1 基于KGC-WGAN的在线交易反欺诈方法本文提出了一种基于特征优化生成对抗网络的在线交易反欺诈方法,同时结合CGAN[14]、WGAN[15]和Gumbel-softmax提出了KGC-WGAN(key feature and Gumbel-softmax conditional WGAN)模型用于交易欺诈数据的生成。其核心思想是在不丢失原始信息的前提下,利用KGC-WGAN模型生成足够真实的欺诈数据扩充数据集,同时优化生成数据的质量和提高训练过程的稳定性,解决在线交易数据严重不平衡问题和生成对抗网络处理离散的在线交易数据效果不佳、训练不稳定的问题。基于KGC-WGAN的在线交易反欺诈方法的系统总流程如图 1所示。主要包括三个部分:数据预处理、生成对抗网络模型、模型评估。
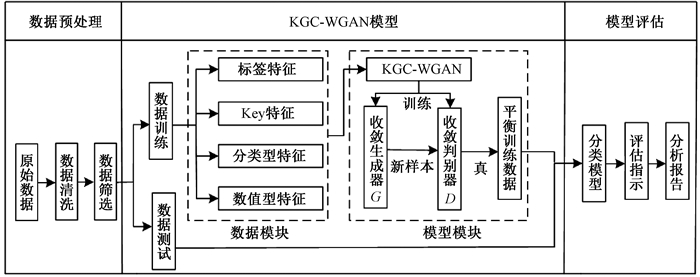
|
图 1 系统流程图 Fig. 1 System flow chart |
1) 数据预处理:对原始的数据通过数据清理和数据集成等方法将数据转换成可参与模型计算的形式。
2) KGC-WGAN模型:KGC-WGAN模型主要有两个部分:第一部分是数据模块,对训练数据进行标签特征、Key特征、分类型特征和数值型特征的分类和提取;第二部分是模型模块,首先将数据模块处理后的数据输入到KGC-WGAN模型中进行模型训练直至收敛,接着利用收敛后的生成模型G生成伪数据,最后将生成的伪数据输入到收敛的判断模型D中进行识别,将被判别为真的生成数据与原始数据融合,对原始数据进行平衡处理。
3) 模型评估:利用经过平衡处理后的数据对分类模型进行训练,对交易数据进行预测评估并生成分析报告。
1.1 KGC-WGAN模型 1.1.1 数据处理针对交易数据的特点,KGC-WGAN模型首先会对交易数据的特征进行分类。根据特征的数据类型和重要程度将特征分为数值型特征、分类型特征、Key特征和标签特征。Key特征的获取是通过基于随机森林对特征进行重要性排序或者根据实际业务中的重要程度进行Key特征选择。针对不同类型的Key特征进行不同的处理:对于类别类型的Key特征进行类别随机采样;对于数值型的Key特征进行分层随机采样。
1.1.2 模型结构KGC-WGAN模型由一个生成器G和一个判别器D构成。生成器G的结构由3个部分构成:首先根据一个正态分布z~N(0, 0.01) 进行随机采样得到噪声Z,然后对Key特征和标签特征进行随机采样得到X_key和Y;接着将Z、X_key输入到n个隐藏层和归一化层,然后对隐藏的一部分输出进行Gumbel-softmax采样,得到分类型特征X_cat,另一部分输出得到数值型特征X_num;最后将X_cat、X_num、X_key和Y进行连接,得到最终的生成样本。判别器D的结构由3个部分构成:首先对输入样本的X_cat特征进行编码,然后将编码后的向量和X_num、X_key、Y输入到n个相连的隐藏层和归一化层,经过一个线性层和一个归一化层得到一个为真实数据和生成数据的概率向量。
1.2 算法实现基于KGC-WGAN的在线交易反欺诈方法的具体实现步骤如算法1所示。
算法1 基于KGC-WGAN的在线交易反欺诈算法。
输入:交易数据X,分类算法C,噪声z。
输出:分类算法C的评估指标M。
Step1 创建KGC-WGAN模型:建立生成网络G和判别网络D。
Step2 对数据进行处理:分类和提取X_key、X_cat、X_num和label特征。
Step3 生成网络G生成数据:生成噪声z,采样得到key特征X_key和标签Y,将z、X_key输入到生成网络G进行数据生成,在G生成数据过程中进行Gumbel-softmax技巧采样输出,得到X_cat和X_num,将X_key、X_cat、X_num和Y连接得到生成数据Xg。
Step4 更新判别网络D参数:将原始数据X和生成数据Xg同时输入判别模型得到损失值Loss,进行模型训练并且更新判别网络D的参数w。
Step5 更新生成网络G参数θ:将判别网络D的损失值Loss反馈给生成网络进行训练,并更新参数。
Step6 重复Step2~4直到生成网络G的θ收敛。
Step7 数据平衡处理:利用Step5得到收敛的生成网络G生成的欺诈数据,对原始数据扩充,并进行处理,得到平衡的交易数据Xn。
Step8 模型评估:将平衡处理后的数据Xn输入到分类算法C中进行训练,并得到评估指标M。
2 实验与分析 2.1 评价指标为了验证使用KGC-WGAN模型平衡数据后对分类效果的影响,实验所选用的评价指标有F1值、AUC_ROC、AUC_PR和Brier值。AUC_ROC和AUC_PR值分别为ROC曲线和PR曲线下的面积,Brier值计算公式为
| $ { Brier }=\frac{1}{N} \sum\limits_{i=1}^{N}\left({ pred }_{i}- { label }_{i}\right)^{2}, $ |
其中:N是样本数;predi是属于正类的预测概率;labeli是真正的类标签。对于Brier评分来说,值越低越好,而对于AUC_ROC和AUC_PR来说,则值越高越好。
2.2 实验环境与实验数据 2.2.1 实验环境实验采用的环境CPU为Intel Core i7,RAM为24 GB,实验所有代码都是基于Python开发实现。
2.2.2 实验数据本文实验的数据(表 1)包括两个大规模数据集和两个小规模数据集。
|
|
表 1 实验数据集 Tab. 1 Experimental datasets |
经过缺失值处理、特征筛选和归一化处理后数据集的情况见表 1。两个大规模数据包括1) ATEC数据集:2018年蚂蚁金服公司举办的ATEC大赛,风险支付识别赛事公开提供的脱敏后的在线交易支付数据;2) Lendingclub数据集:Lendingclub平台的2018年第三季度的数据。两个小规模数据集包括German数据集和HomeEquity数据集。
2.3 实验过程与分析为了验证本文提出的KGC-WGAN模型的有效性,主要对生成数据质量、重采样后分类、不同采样比进行对比分析。
2.3.1 生成数据质量分析生成数据的质量是判断生成模型好坏的一个重要评判指标,但是目前还没有一种公认的测量结构化数据集相似性的方法,因此本文使用了几种不同的度量方法。1) 对于数值型特征,本文对真实数据和生成数据的概率分布进行了比较,比较情况如图 2所示。每一个小图对应的是一个特征的概率分布比较情况,其中横轴为特征经过标准化处理后的值,纵轴为对应的概率密度。从图 2可以看出,对特征如LOAN这类概率分布比较简单的数据,KGC-WGAN模型生成的数据非常接近原始数据集的数据分布,拟合效果比较好。但是对特征如YOJ这类概率分布比较复杂的数据,模型的生成数据拟合效果不是很好。
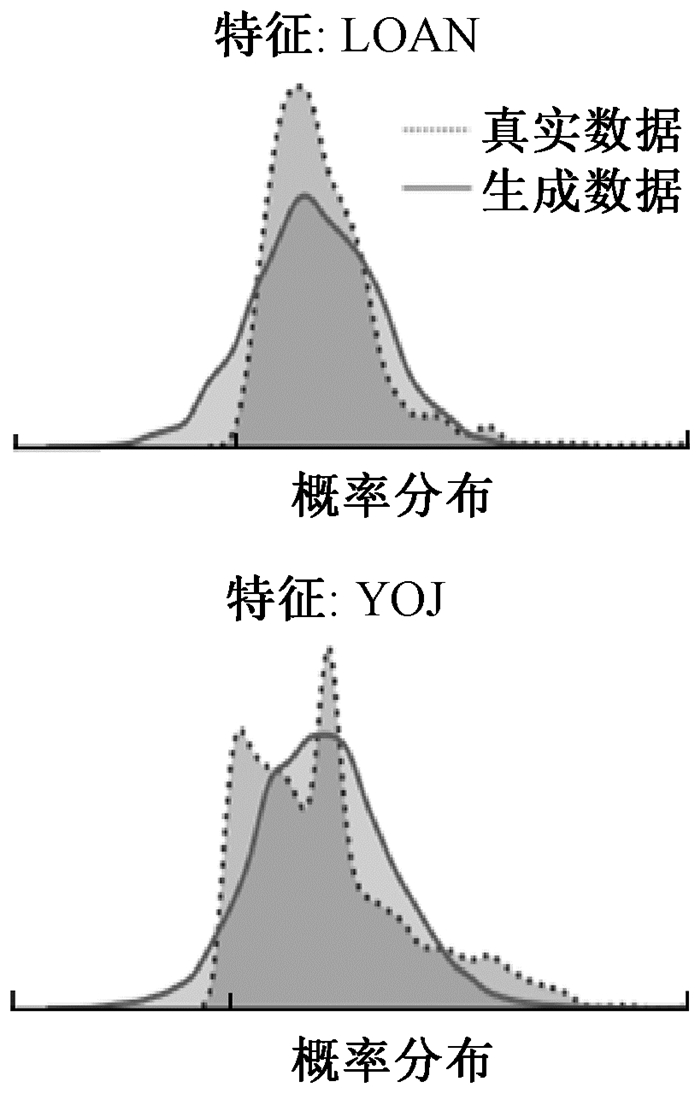
|
图 2 数值型变量分布 Fig. 2 Numerical variable distribution |
2) 对于类别型特征,本文对生成数据和真实数据中每一个类别的样本数进行了比较,如图 3所示。图中横轴为特征值,每一个值对应的就是一个类别。从图 3可以看出,除少数类别样本数量差距较大,如REASON中的类别3样本和JOB中的类别3样本,KGC-WGAN模型的生成数据中类别型特征中每个类别的样本数量和真实数据的样本数量总体上比较接近。
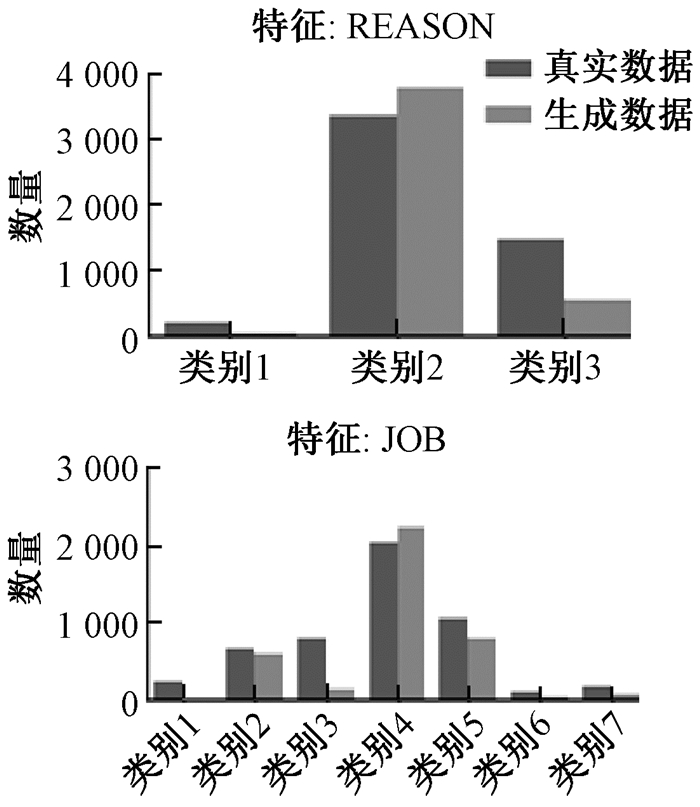
|
图 3 类别型变量分布 Fig. 3 Categorical variable distribution |
可以看出KGC-WGAN模型生成数据整体质量还是不错的,基本上能够拟合真实数据,但是对于复杂的数据拟合效果还是有待提升。
2.3.2 重采样后分类实验对比分析提高模型重采样的性能、降低数据不平衡性的影响是解决在线交易反欺诈最重要的目标,目前SMOTE方法是最常用和效果最好的重采样方法之一,所以本文选择SMOTE、B-SMOTE和ADASYN算法作为KGC-WGAN模型的对比重采样方法。对于重采样后数据的分类,本文选用了3个分类器:逻辑回归(LG)、Adaboost(ADAB)和XGboost(XGB),通过不同分类器分类结果对比分析本文方法与其他采样方法效果。所有数据集在经过不同的方法重采样和不同的分类器分类后的实验结果如表 2所示,表中粗体的数据代表相应的最佳实验结果。
经过对表 2的对比分析,可以得到以下结论。
|
|
表 2 不同重采样方法实验结果 Tab. 2 Experimental results of different resampling methods |
1) 在所有的实验结果中,KGC-WGAN模型重采样的F1值在几乎所有的分类器上都是高于其他方法的,只有German数据集在LG分类器上的效果不是最佳。
2) 实验数据集在使用KGC-WGAN模型重采样后,经过XGB分类器分类后的每个指标都是所有重采样方法中最好的,这说明经过KGC-WGAN模型重采样的数据能够很好地与XGB分类器契合。整体来看,KGC-WGAN模型处理后的数据在LG分类器的表现最差,在XGB分类器的表现最好,在ADAB分类器的表现居中。
3) KGC-WGAN模型在ATEC数据集和Lendingclub数据集上的整体表现是优于其他数据集的,而ATEC和Lendingclub都是大规模的数据集,并且带有类别向量。这可以说明KGC-WGAN模型中的Gumbel-softmax方法是适用于类别变量的,从而说明该模型更适合大规模且带有类别变量的数据集。
2.3.3 不同采样比实验对比分析为了探究数据集的不平衡程度对于欺诈检测的影响,针对数据集进行了不同的采样率的实验,实验选取了5种正负样本比例,分别为100∶1、10∶1、1∶1、1∶10、1∶100,利用KGC-WGAN模型生成的少数类样本对原始数据进行不同比例的平衡处理,进行不同比率采样后,3种分类器分类后的实验结果如表 3所示。
|
|
表 3 不同采样比率实验结果 Tab. 3 Experimental results of different sampling ratio |
从表 3可以得出以下几点结论。
1) 指标F1、AUC_ROC、AUC_PR整体上正负样本比为100∶1和10∶1的数据集的分类效果更好。Lendingclub、HomeEquity和German数据集在正负样本比为10∶1的时候分类效果最佳,ATEC数据集在正负样本比为100∶1的时候分类效果最佳。对于不平衡的交易数据样本的分类,少数类的采样比例应该是稍低于或者接近于多数类样本,而尽量不超过多数类样本数。因为对少数类样本进行重采样过多,重采样的不确定性会使数据集偏离真实数据的分布,进而干扰分类器的分类效果。
2) 在Brier指标上,LG和ADAB分类器在正负样本比为1∶100时效果最好。XGB分类器在正负样本比1∶1和100∶1时效果最好。可以总结出XGB分类器处理负样本比例较低的数据集的效果更好,更适合处理交易欺诈数据。
综上,可以得出:a) 通过生成数据质量实验分析可以看出,KGC-WGAN模型生成的交易数据能够较好地拟合原始交易数据,但是对于复杂分布的数据的生成质量还有提升的空间;b) 通过重采样后分类对比分析,可以总结出KGC-WGAN在一定程度上解决了原始数据不平衡对分类结果的影响,并且在整体效果上优于其他算法;c) 通过不同采样比分析的结果可以看出样本的平衡性在一定程度上影响了分类器效果,总体上是欺诈样本比例稍低于正常样本比例的时候,分类效果最佳。
3 结束语针对在线交易数据的不平衡问题对欺诈检测的影响,提出了一种基于特征优化生成对抗网络的在线交易反欺诈方法。该方法利用KGC-WGAN生成少数类数据对原始数据进行平衡处理,在生成数据时加入Key特征提高生成数据的质量以及后续训练的稳定性,利用Gumble-softmax技巧解决交易数据中类别数据的生成梯度消失问题。实验结果表明该方法有效改善了原始数据的不平衡问题,减小了数据不平衡性对分类器预测能力的影响,并且整体效果优于其他对比。今后的研究方向是提高复杂分布数据的生成质量,提高本文方法的适用范围。
| [1] |
李艳霞, 柴毅, 胡友强, 等. 不平衡数据分类方法综述[J]. 控制与决策, 2019, 34(4): 673-688. LI Y X, CHAI Y, HU Y Q, et al. Review of imbalanced data classification methods[J]. Control and decision, 2019, 34(4): 673-688. (  0) 0) |
| [2] |
CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of artificial intelligence research, 2002, 16: 321-357. DOI:10.1613/jair.953 (  0) 0) |
| [3] |
DÍEZ-PASTOR J F, RODRÍGUEZ J J, GARCÍA-OSORIO C, et al. Random balance: ensembles of variable priors classifiers for imbalanced data[J]. Knowledge-based systems, 2015, 85: 96-111. DOI:10.1016/j.knosys.2015.04.022 (  0) 0) |
| [4] |
杨毅, 卢诚波, 徐根海. 面向不平衡数据集的一种精化Borderline-SMOTE方法[J]. 复旦学报(自然科学版), 2017, 56(5): 537-544. YANG Y, LU C B, XU G H. A refined borderline-SMOTE method for imbalanced data set[J]. Journal of fudan university (natural science), 2017, 56(5): 537-544. (  0) 0) |
| [5] |
石洪波, 陈雨文, 陈鑫. SMOTE过采样及其改进算法研究综述[J]. 智能系统学报, 2019, 14(6): 1073-1083. SHI H B, CHEN Y W, CHEN X. Summary of research on SMOTE oversampling and its improved algorithms[J]. CAAI transactions on intelligent systems, 2019, 14(6): 1073-1083. (  0) 0) |
| [6] |
蒋华, 江日辰, 王鑫, 等. ADASYN和SMOTE相结合的不平衡数据分类算法[J]. 计算机仿真, 2020, 37(3): 254-258, 420. JIANG H, JIANG R C, WANG X, et al. Unbalanced data classification algorithm based on combination of ADASYN and SMOTE[J]. Computer simulation, 2020, 37(3): 254-258, 420. DOI:10.3969/j.issn.1006-9348.2020.03.053 (  0) 0) |
| [7] |
CHEN T, HE T. Higgs boson discovery with boosted trees[C]//International Conference on High-energy Physics & Machine Learning. New York: ACM Press, 2014: 69-80.
(  0) 0) |
| [8] |
KRAWCZYK B, WOZ·NIAK M, SCHAEFER G. Cost-sensitive decision tree ensembles for effective imbalanced classification[J]. Applied soft computing, 2014, 14: 554-562. DOI:10.1016/j.asoc.2013.08.014 (  0) 0) |
| [9] |
王忠震, 黄勃, 方志军, 等. 改进SMOTE的不平衡数据集成分类算法[J]. 计算机应用, 2019, 39(9): 2591-2596. WANG Z Z, HUANG B, FANG Z J, et al. Improved SMOTE unbalanced data integration classification algorithm[J]. Journal of computer applications, 2019, 39(9): 2591-2596. (  0) 0) |
| [10] |
GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2014: 2672-2680.
(  0) 0) |
| [11] |
冯永, 张春平, 强保华, 等. GP-WIRGAN: 梯度惩罚优化的Wasserstein图像循环生成对抗网络模型[J]. 计算机学报, 2020, 43(2): 190-205. FENG Y, ZHANG C P, QIANG B H, et al. GP-WIRGAN: a novel image recurrent generative adversarial network model based on Wasserstein and gradient penalty[J]. Chinese journal of computers, 2020, 43(2): 190-205. (  0) 0) |
| [12] |
张敏情, 李宗翰, 刘佳, 等. 基于边界平衡生成对抗网络的生成式隐写[J]. 郑州大学学报(理学版), 2020, 52(3): 34-41. ZHANG M Q, LI Z H, LIU J, et al. Generative steganography based on boundary equilibrium generative adversarial network[J]. Journal of Zhengzhou university (natural science edition), 2020, 52(3): 34-41. (  0) 0) |
| [13] |
ENGELMANN J, LESSMANN S. Conditional Wasserstein GAN-based oversampling of tabular data for imbalanced learning[J]. Expert systems with applications, 2021, 174: 114582. DOI:10.1016/j.eswa.2021.114582 (  0) 0) |
| [14] |
MIRZA M, OSINDERO S. Conditional generative adversarial nets[EB/OL]. (2014-11-06)[2020-12-15]. https://arxiv.org/pdf/1411.1784.pdf.
(  0) 0) |
| [15] |
MARTIN A, SOUMITH C, LÉON B. Wasserstein GAN. (2017-01-26)[2020-12-15]. https://arxiv.org/pdf/1701.07875.pdf.
(  0) 0) |
 2022, Vol. 54
2022, Vol. 54


