在机器学习中,虽然多标记学习已经能处理很多标记模糊问题[1].但现实中有着更多的关于每个标记对实例准确描述度的数据.例如,人脸年龄估计[2]、图像识别问题[3]以及基因在不同时间点上的表达水平[4],这些数据并不是多标记学习能够完善处理的.为了准确地反映每个标记对实例的描述程度,文献[4]提出了针对标记分布的学习算法和学习范式.图 1为包含天空、水、建筑和云的多标记自然场景图像[5],如图 2中表示一个概率分布的数据形式即为标记分布.

|
图 1 包含天空、水、建筑和云的多标记自然场景图像 Figure 1 A multiple labels natural scene image which has been annotated with sky, water, building and cloud |
|
图 2 自然场景图像相应的标记分布图像 Figure 2 Label distribution of the natural scene image |
标记分布学习是一种新型学习范式,近几年来成为机器学习中的热点研究问题之一[6-10].最初研究者们基于标记分布的思想设计了相应的IIS-LLD算法和CPNN算法[6].这两种算法由于在训练过程中能够利用更多的样本信息,因此取得了更好的效果.文献[7]提出完整的标记分布学习框架,该框架不仅形式化地定义了标记分布学习,而且设计了标记分布学习算法,还给出了衡量标记分布学习算法性能的指标.
根据算法设计策略的不同,标记分布学习分为问题转换法、算法适应法和专门的算法三种[7],问题转换法是指将标记分布学习转换为多实例学习或者多实例多标记学习,例如PT-Bayes算法和PT-SVM算法.算法适应法是指自然扩展某些已有的有标记学习算法,使扩展后的算法能够处理标记分布问题,例如AA-KNN算法和AA-BP算法.专门的算法是指直接通过条件概率或者逻辑回归等概率思想建立模型,例如SA-IIS算法和LDLogitBoost算法[11].相对于问题转换和算法适应,标记分布学习中的专门算法在实际应用中有更好的表现.目前,标记分布学习中的专门算法主要是通过KL散度(kullback-leibler divergence)建立参数模型[3-4],并利用最大熵[12]和逻辑回归[13]等不同模型为参数模型进行推导,这个过程在某种程度上忽略了特征与标记之间的函数关系.
针对标记分布的特性,利用最小二乘法建立标记分布学习模型[14-15].最小二乘法是通过最小化误差的平方和寻找数据的最佳函数匹配[16-19].针对标记分布学习中标记的特点,并受最小二乘法的启发,本文提出了基于最小二乘的标记分布学习方法(lsm-LDL).首先用特征信息通过线性重构的方式重构标记分布,以重构标记与原始标记的最小误差建立模型;然后引入最小二乘法,通过最小化误差的平方和优化模型;最后为了防止训练过程中的过拟合问题,并考虑到稀疏解还能够有效地减小噪声的影响[20-21],所以联合L2范数正则化项求解重构矩阵,从而得到预测标记分布.为了验证提出算法的有效性,分别在4个公开数据集上进行算法效果评估实验,结果表明提出的标记分布学习算法具有较好的效果.
1 相关工作标记分布对每一个实例x,为它的每一个可能的标记y,分配一个实数dxy,这个实数用来表示标记y描述实例x的程度,即描述度.不失一般性,假设dxy∈[0, 1],且所有的标记能够完整地描述实例,则
标记分布学习定义给定的实例集为X,X=[x1, x2, …, xn]T,xi∈Rm表示第i个实例,i=1, 2, …, n,相应的实例集用特征可表示为X=[f1, f2, …, fm],fj∈Rn表示第j个特征,j=1, 2, …, m.给定样本对应的标记集为Y=[y1, y2, …, yc],yk∈Rn表示第k个标记,k=1, 2, …, c.给定样本相对应的标记分布集为D,D=[D1, D2, …, Dn]T,Di=[dxiy1, dxiy2, …, dxiyc]表示实例xi的标记分布集,dxiyk表示标记yk对实例xi的描述度.因此,在文中标记分布学习的训练集为S,S=[(x1, D1), …, (xi, Di), …, (xn, Dn)]T.另外,将重构矩阵定义为T,T=[tjk]∈Rd×c,tjk是重构矩阵第j行、第k列对应位置的元素.
标记分布学习算法使用KL散度作为概率分布之间的距离标准进行建模,建立优化模型[7]
| $ {{\mathit{\boldsymbol{\theta}} }^{*}}=\text{arg}\ \underset{\theta }{\mathop{\text{min}}}\, \sum\limits_{i}{\sum\limits_{k}{d_{{{\mathit{\boldsymbol{x}}}_{i}}}^{{{\mathit{\boldsymbol{y}}}_{k}}}\text{ln}\frac{d_{{{\mathit{\boldsymbol{x}}}_{i}}}^{{{\mathit{\boldsymbol{y}}}_{k}}}}{p\left( \mathit{\boldsymbol{y}}/\mathit{\boldsymbol{x}};\theta \right)}, }} $ | (1) |
其中:p(y/x; θ)是参数模型;θ是参数向量数;θ*是最优参数向量.通过最大熵模型或逻辑回归模型输出标记分布[6, 8],现有多种基于式(1)的标记分布学习算法[3, 4, 6],这些算法通过条件概率建立参数模型,利用现有的模型作为参数模型求解参数.但这些方法没有从函数的角度考虑特征与标记间的紧密关联.
2 基于最小二乘的标记分布学习算法基于线性重构,用数据的特征直接重构标记,那么对于每个特征和每个标记有关系
| $ \mathit{\boldsymbol{D}}=\mathit{\boldsymbol{XT}} $ | (2) |
其中:T=[tjk]∈Rm×c是特征对标记的重构矩阵;tjk表示第j个特征对第k个标记的重构系数.
对于给定的数据集S,其中X的维度n > m.显然,对于式(2),一般情况下是无解的[21].所以引入最小二乘法,为了选取最合适的T,基于最小二乘式(3)中引入残差平方和函数L
| $ L\left( \mathit{\boldsymbol{T}} \right)=\left\| \mathit{\boldsymbol{XT}}-\mathit{\boldsymbol{D}} \right\|_{2}^{2}, $ | (3) |
| $ \mathit{\boldsymbol{\hat{T}}}=\text{arg}\ \underset{\mathit{\boldsymbol{T}}}{\mathop{\text{min}}}\, L(\mathit{\boldsymbol{T}})\text{, } $ | (4) |
式(4)对T进行微分有
| $ L\left( \mathit{\boldsymbol{T}} \right)=\underset{\mathit{\boldsymbol{T}}}{\mathop{\rm{min}}}\, \left\| \mathit{\boldsymbol{XT}}-\mathit{\boldsymbol{D}} \right\|_{2}^{2}+\gamma \left\| \mathit{\boldsymbol{T}} \right\|_{2}^{2}, $ | (5) |
其中γ为规则化项参数.式(5)中L2范数可通过导数求解[25].将函数L(T)对T求导并令其为零,有
| $ \frac{\partial L\left( \mathit{\boldsymbol{T}} \right)}{\partial \mathit{\boldsymbol{T}}}=2{{\mathit{\boldsymbol{X}}}^{\rm{T}}}\mathit{\boldsymbol{XT}}-2{{\mathit{\boldsymbol{X}}}^{\rm{T}}}\mathit{\boldsymbol{D}}+2\gamma \mathit{\boldsymbol{T}}=0, $ | (6) |
由式(6)可得
| $ \mathit{\boldsymbol{T}}={{({{\mathit{\boldsymbol{X}}}^{\rm{T}}}\mathit{\boldsymbol{X}}+\gamma \mathit{\boldsymbol{I}})}^{-1}}{{\mathit{\boldsymbol{X}}}^{\rm{T}}}\mathit{\boldsymbol{D}}, $ | (7) |
这样添加L2范数规则项的方法既能够保证位置变量T有唯一解,又能在一定程度上防止过拟合.式(7)中求得的T即为训练集通过lsm-LDL算法学习获得的重构矩阵.那么预测标记D′=X′T,其中X′为测试集实例.由于
| $ {{\mathit{\boldsymbol{D}}}_{i}}^{\prime \prime }=\frac{\left| {{{\mathit{\boldsymbol{{D}'}}}}_{i}} \right|}{\sum{{{{\mathit{\boldsymbol{{D}'}}}}_{i}}}}. $ | (8) |
基于上述分析,提出的lsm-LDL算法具体步骤如下:
输入:规则化参数D″,训练集D.输出:测试集的预测标记分布D″.
步骤1:通过式(7)计算T.步骤2:用D′=X′T计算预测标记.步骤3:计算式(8),有归一化标记分布D″.
3 实验与结果分析通过实验验证提出的基于最小二乘的标记分布学习(lsm-LDL)算法,相对于其他的对比算法具有更好的实验效果.利用评价标记分布间的相似性或者距离的评价方式,作为标记分布的评价指标[5].文献[26]中提出8个不同族的41种评价方法,都能用于这样的评价.用凝聚单联动与平均聚类方法建立关系值[27],根据文献[6]提出的筛选规则及实验条件选出5种评价方法.分别是切比雪夫距离(Cheb)、克拉克距离(Clark)、堪培拉量度(Canber)、余弦系数(Cosine)以及交叉相似性(Intersec).具体的评价方法的计算公式如表 1所示.前3个指标是距离指标,值越小表示效果越好, 后2个指标是相似指标,值越大表示算法效果越好.
|
|
表 1 5种评价指标的名称、公式 Table 1 Name and formula of five evaluation indexes |
实验过程,用4个公开数据(http://cse.seu.edu.cn/PersonalPage/xgeng/LDL/index.htm)进行实验:分别是数据集Yeast-alpha、Yeast-cold、Human Gene和Moive.lsm-LDL算法的平衡参数设置为{103, 102, 101, 1, 10-1, 10-2, 10-3},记录算法最好的结果所对应的参数,以最佳参数作为下文参数的取值[23].上述4个数据集的简要信息及对应的最好结果的参数值,如表 2所示.
|
|
表 2 实验数据集描述 Table 2 The description of experimental data set |
实验采用十折交叉验证进行,测试结果用3种距离和2种相似指标进行评价,最终结果为测试集标记分布的均值.与3种现有经典标记分布学习算法在公开数据集上进行对比实验.对比算法[6]分别是问题转换算法PT-Bayes、算法适应算法AA-kNN和专门的算法IIS-LDL.
3.2 实验结果分析表 3~6分别列出在4个不同数据集上,每种算法在不同评价指标的衡量下的值.表中的值用粗体表示最优结果,下划线表示次优结果.
|
|
表 3 数据集Yeast-alpha的实验结果 Table 3 The experimental results of data set Yeast-alpha |
|
|
表 4 数据集Yeast-cold的实验结果 Table 4 The experimental results of data set Yeast-cold |
|
|
表 5 数据集Moive的实验结果 Table 5 The experimental results of data set Moive |
|
|
表 6 数据集Human Gene的实验结果 Table 6 The experimental results of data set Human Gene |
表 3列出数据集Yeast-alpha在5种不同指标下对应的4种算法的表现,从表中可看到提出的lsm-LDL算法在该数据集上明显比其他3种对比算法有更好的结果.另外,算法AA-kNN在该数据集上也有较好的结果.表 4和表 5列出不同算法在数据集Yeast-cold和数据集Movie上对应5种不同指标的结果,从表中可以看到提出的lsm-LDL算法在该数据集上明显比其他3种对比算法有更好的结果.在这两个数据集上仍然是AA-kNN算法有第二好的结果,同时可看到IIS-LDL算法在这2个数据集上有个别指标具有第二好的结果.表 6列出各个算法在数据集Human Gene上不同指标对应的结果,lsm-LDL算法在该数据集上仍然明显比其他3种对比算法有更好的结果.另外,IIS-LDL算法在该数据集上的结果仅次于我们提出的lsm-LDL算法.
综上所述,从表 3到表 6可以看出,提出的lsm-LDL算法不仅在5种评价指标下都有较好的效果,而且在各个数据集上都能够保持较好的性能,相对于其他3种算法有更强的适应性和稳定性.我们提出的算法比传统的概率模型不仅求解快速,而且具有更强的适应能力和更好的稳定性.
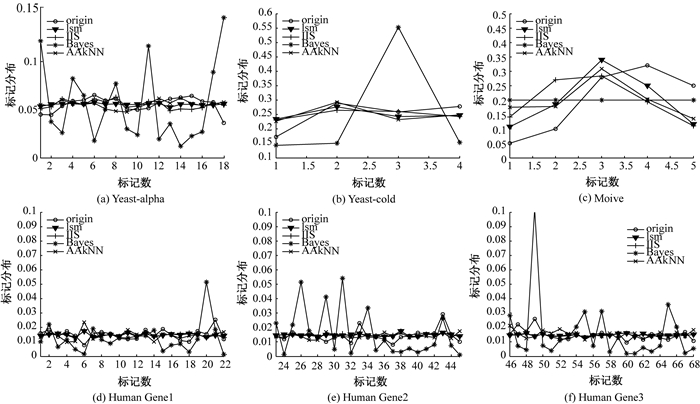
图 3呈现不同算法学习得来的某一实例的预测标记分布和原始标记分布的趋势.纵坐标代表标记分布,横坐标表示标记数.其中图(a)、(b)和(c)分别表示数据集Yeast-alpha、Yeast-cold和Moive的测试集中的最中间一个实例的标记分布图,每个图中包括原始标记分布,以及4种算法学习获得的预测标记分布,分别用不同的折线表示.由于数据集Human Gene标记较多,所以将标记分为3部分,由图(d)、(e)和(f)共同表示数据集Human Gene的测试集中的最中间一个实例的标记分布.从图 3中可以看出lsm-LDL算法获得的标记分布与原始标记分布较为接近,说明lsm-LDL算法在这4个数据集上相对于对比算法有更好的效果.
|
图 3 不同标记分布学习算法预测的标记分布及原始标记分布 Figure 3 Label distribution of different label distribution learning algorithms and original label distribution |
综合表 3~表 6和图 3的分析,提出的算法相较于其他3种对比算法能够得到更加接近于原始标记分布的预测标记分布,并且在3种距离评价指标和2种相似评价指标上都有较好的表现.
4 总结标记分布学习不仅能够处理一个示例有多个标记的问题,而且还能得到各个标记对示例的重要程度.文中提出的lsm-LDL算法,根据训练集的原始标记分布与通过线性重构的预测标记分布之间最小误差建立模型,利用最小二乘法并联系规则化项L2范数优化求解.通过训练集学习获得一个重构矩阵,重构矩阵和测试集特征数据以矩阵相乘的方式重构测试集标记分布,从而获得测试集的预测标记.lsm-LDL算法在4个公开数据集上进行实验,比较于传统的概率模型,不仅求解过程速度快,而且具有更强的适应能力和更好的稳定性.
| [1] |
WANG J, YANG Y, MAO J, et al. CNN-RNN: a unified framework for multi-label image classification[C]//IEEE Computer Society, Proceeding of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, 2016:2285-2294.
(  0) 0) |
| [2] |
GENG X, ZHOU Z H, SMITH-MILES K. Automatic age estimation based on facial aging patterns[J]. IEEE transactions on pattern analysis and machine intelligence, 2007, 29(12): 2234-2240. DOI:10.1109/TPAMI.2007.70733 (  0) 0) |
| [3] |
ZHANG Z, WANG M, GENG X. Crowd counting in public video surveillance by label distribution learning[J]. Neuro computing, 2015, 166(C): 151-163. (  0) 0) |
| [4] |
季荣姿. 标记分布学习及其应用[D]. 南京: 东南大学, 2014. http://d.g.wanfangdata.com.cn/Thesis_Y2707526.aspx
(  0) 0) |
| [5] |
LI Y K, ZHANG M L, GENG X. Leveraging implicit relative labeling-importance information for effective multi-label learning[C]//IEEE International Conference on Data Mining. Atlantic City, 2015, 6(2): 251-260.
(  0) 0) |
| [6] |
GENG X, YIN C, ZHOU Z H. Facial age estimation by learning from label distributions[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(10): 2401-2412. DOI:10.1109/TPAMI.2013.51 (  0) 0) |
| [7] |
GENG X. Label distribution learning[J]. IEEE transactions on knowledge and data engineering, 2016, 28(7): 1734-1748. DOI:10.1109/TKDE.2016.2545658 (  0) 0) |
| [8] |
BOUTELL M R, LUO J, SHEN X, et al. Learning multi-label scene classification[J]. Pattern recognition, 2004, 37(9): 1757-1771. DOI:10.1016/j.patcog.2004.03.009 (  0) 0) |
| [9] |
ZHANG M L, ZHOU Z H. A review on multi-label learning algorithms[J]. IEEE transactions on knowledge and data engineering, 2014, 26(8): 1819-1837. DOI:10.1109/TKDE.2013.39 (  0) 0) |
| [10] |
MEERBERGEN K, ROOSE D. Matrix transformations for computing rightmost eigenvalues of large sparse non-symmetric eigenvalue problems[J]. IMA journal of numerical analysis, 1996, 16(3): 297-346. DOI:10.1093/imanum/16.3.297 (  0) 0) |
| [11] |
XING C, GENG X. Logistic boosting regression for label distribution learning[C]. IEEE International Conference on Computer Vision and Pattern Recognition. Las Vegas, 2016: 4489-4497. http://ieeexplore.ieee.org/document/7780855/
(  0) 0) |
| [12] |
BERGER A, PIETRA V, PIETRA S. A maximum entropy approach to natural language processing[J]. Computational linguistics, 2002, 22(1): 39-71. (  0) 0) |
| [13] |
COLLINS M, SCHAPIRE R E, SINGER Y. Logistic regression, adaboost and bregman distances[J]. Machine learning, 2002, 48(1): 253-285. (  0) 0) |
| [14] |
TSOUMAKAS G, KATAKIS I, DAVID T. Multi-label classification: an overview[J]. International journal of data warehousing & mining, 2007, 3(3): 1-13. (  0) 0) |
| [15] |
RUST B W. Fitting nature′s basic functions part Ⅲ: exponentials, sinusoids, and nonlinear least squares[J]. Computing in science and engineering, 2002, 4(4): 72-77. DOI:10.1109/MCISE.2002.1014982 (  0) 0) |
| [16] |
贾小勇, 徐传胜, 白欣. 最小二乘法的创立及其思想方法[J]. 西北大学学报(自然科学版), 2006, 36(3): 507-511. (  0) 0) |
| [17] |
陆健. 最小二乘法及其应用[J]. 中国西部科技, 2007(19): 19-21. (  0) 0) |
| [18] |
SUYKENS J A K, GESTEL VT, BRABANTER J D. Least square support sector machine[J]. Euphytica, 2002, 2(2): 1599-1604. (  0) 0) |
| [19] |
VAPNIK V. The nature of statistical learning theory[M]. New York: Springer Science and Business Media, 2013.
(  0) 0) |
| [20] |
NIE F, HUANG H, CAI X, et al. Efficient and robust feature selection via joint  0) 0) |
| [21] |
脱倩娟, 赵红. 基于局部邻域嵌入的无监督特征选择[J]. 郑州大学学报(理学版), 2016, 48(3): 57-62. (  0) 0) |
| [22] |
马丽, 董唯光, 梁金平, 等. 基于随机投影的正交判别流形学习算法[J]. 郑州大学学报(理学版), 2016, 48(1): 102-109. (  0) 0) |
| [23] |
ZHU P, ZUO W, ZHANG L, et al. Unsupervised feature selection by regularized self-representation[J]. Pattern recognition, 2015, 48(2): 438-446. DOI:10.1016/j.patcog.2014.08.006 (  0) 0) |
| [24] |
何秀丽. 多元线性模型与岭回归分析[D]. 武汉: 华中科技大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10487-2006038843.htm
(  0) 0) |
| [25] |
YU S, FALCK T, DAEMEN A, et al. L2 norm multiple kernel learning and its application to biomedical data fusion[J]. BMC bioinformatics, 2010, 11(1): 1-24. DOI:10.1186/1471-2105-11-1 (  0) 0) |
| [26] |
CHA S H. Comprehensive survey on distance/similarity measures between probability density functions[J]. International journal of mathematical models and methods in applied sciences, 2007, 1(4): 300-307. (  0) 0) |
| [27] |
DUDA R, HART P, STORK D. Pattern classification[M]. 2nd edition. The United States: John Wiley, 2000.
(  0) 0) |
 2017, Vol. 49
2017, Vol. 49


