2. 吉林大学 仪器科学与电气工程学院 吉林 长春 130026
2. College of Instrumentation & Electrical Engineering, Jilin University, Changchun 130026, China
肝储备功能是肝脏所有有效肝细胞所储备功能的总和,是肝脏储备的生理活动临床评估的重要参数.当前临床检测肝储备功能的方法主要通过采血光学比色法实现,为有创检测.随着科技的发展,国内外对无创肝储备功能检测进行了大量研究.文献[1]提出了基于脉搏分光光度法的染料密度测量,实现有效肝血流、血浆消失率等肝储备功能参数测量;文献[2-3]研究了基于ICG脉冲分光光度法在肝切除手术过程中的肝储备功能检测,但该方法检查结果受肝脏血流影响较大,某些特殊患者,如黄疸患者就不适合使用;文献[4]研发了基于色素谱分光光度法的无创肝储备功能参数测量方法及装置,并成功应用于医院临床实验与测试.上述文献多采用光电容积波作为测量对象,实现肝储备功能检测,对获得的光电容积脉搏波信号通常采用高阶数字滤波、均值滤波等方法进行消噪处理[5-7],缺乏对色素谱光电容积波信号的进一步消噪讨论,因此临床应用存在局限性.实际临床无创肝储备功能检测中,光电容积脉搏波信号因其时频域特点,易受到外界干扰和噪声的影响.其中,在测量过程中因病人无意识的肌肉抖动导致的突发干扰对测量结果影响尤为严重,传统的消噪方法,并不能很好解决这个问题,从而难以实现信号的准确检测.
本文提出通过小波变换的方式结合中值滤波算法对肝储备功能分析系统中光电容积波信号的白噪声干扰、突发干扰等干扰进行处理、消噪;与传统消噪方法相比,降低了系统测量误差,保证了实际测量的稳定性,为无创肝储备功能准确检测提供有益的评估和帮助[8-10].
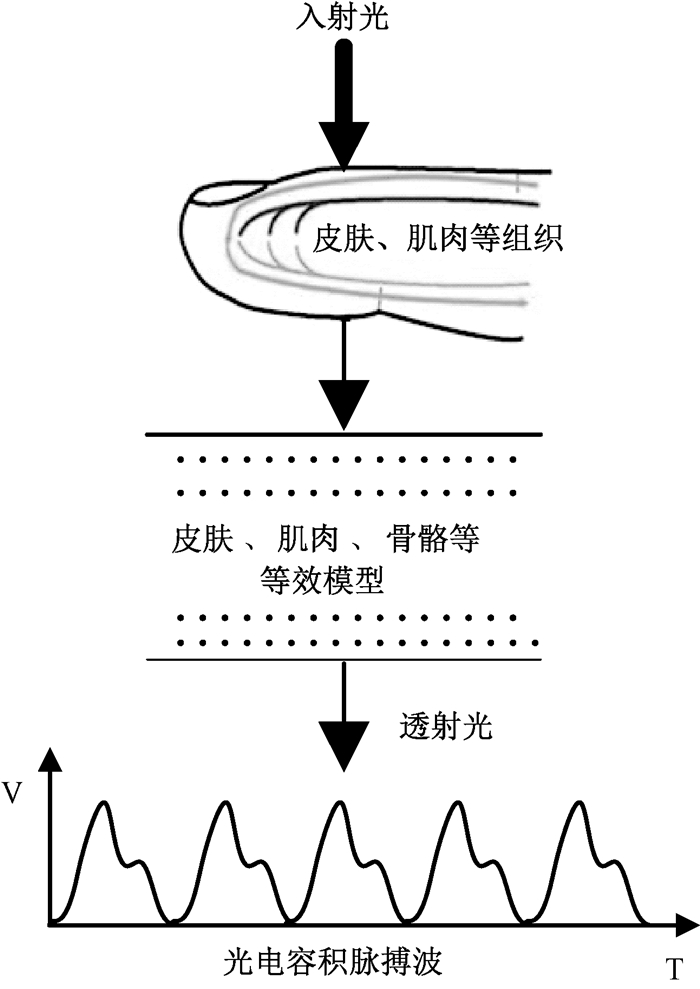
1 光电容积波分析肝储备功能检测是利用光电容积波(PPG)测量方式,在注入吲哚氰绿ICG色素后,利用红光或者红外光和吲哚氰绿ICG色素敏感波形等波长光信号照射指尖端或者耳尖端,探测微血管的血液容积变化.通过透射或者反射方式获取光电波信号,从而获取肝脏对吲哚氰绿ICG色素代谢的人体生理信息,测量肝储备功能[6-7].其测量示意图如图 1所示.

|
图 1 透射光电容积波测量模型 Figure 1 Measurement model of transmission PPG |
光电容积波采用光电技术检测人体血液容积变化,光电容积波时频域信号含有丰富的人体血液生理信息和血流生理信息[11-12].通过测量805 nm和940 nm处光电容积波交直流分量即可测得对应的ICG色素浓度,通过测量时间域范围内的ICG色素浓度值,获得肝储备功能.
2 小波分解与消噪 2.1 小波变换小波分析是时-频分析和多分辨分析的信号处理新技术,能自适应时频信号动态分析的要求.小波变换是信号的时间-尺度分析方法,在时域、频域具有表征信号局部特征的能力,是时间窗和频率窗可调节的分析方法[10-12].ψ(t)为母小波函数,则离散化小波变换为:
其重构变换为
| $ f\left( t \right) = \sum\limits_j {\left\langle {f, {\psi _{j,k}}\left( t \right)} \right\rangle } {{\tilde \psi }_{j,k}}\left( t \right) \approx \frac{2}{{A + B}}\sum\limits_{j,k} {W{T_f}\left( {j,k} \right)} {\psi _{j,k}}\left( t \right), $ |
其中:
SymN小波函数是属于SymletsA函数系的近似对称的紧支集双正交小波,它是db函数的改进形式, SymN系列小波没有具体的表达式和小波基[13].小波分解的方式是一类小波函数与待分解函数的近似逼近,小波形态与分解函数的近似性越好,其逼近效果越好,因此选择Sym8小波函数实现小波分解与消噪,Sym8小波函数和尺度函数如图 2所示.
|
图 2 Sym8小波函数和尺度函数 Figure 2 Sym8 wavelet function and scaling function |
肝储备功能分析系统前端传感检测光电容积波的主要噪声和干扰有:白噪声干扰、突发干扰、随机噪声干扰等,其主要体现在时域波形的基线漂移、波形突变以及波形“毛刺”突出等方面,其中因病人无意识扰动产生的干扰,对测量准确性影响最大.带有突发干扰的肝储备功能光电容积波940 nm、805 nm透射波形如图 3所示.
|
图 3 光电容积波原始信号 Figure 3 PPG original signal |
由快速傅里叶变换(FFT变换),940 nm光电容积脉搏波信号频谱图如图 4所示.

|
图 4 940 nm光电容积脉搏波原始信号频谱图 Figure 4 940 nm PPG original signal frequency spectrogram |
由图 4可知,经肝储备功能分析系统前端传感检测光电容积波,其主要能量成分集中在6 Hz以下,由光电容积波原始信号可以看出,其白噪声干扰和高频干扰存在于原始信号全部时间周期中;肝储备功能测量过程中病人的无意识肌肉抖动,造成的突发干扰如图 5a所示,出现在7~12 s光电容积波信号区间内,采用Sym8小波3层分解,其结果如图 5c~5e所示.

|
图 5 Sym8小波3层分解结果 Figure 5 Decomposition of Sym8 three layers wavelet |
由图 5可知第3层分解的近似系数波形与原始波形形态最为近似,因此采用极值阈值估计法原理的阈值选取规则,以硬阈值方式,重构Det1、Det2、Det3,阈值选取为Det1th1=2.506 3, Det1th2=2.406 3, Det1th3=2.206 3,选取第3层近似系数波形重构[16-18],如图 6所示.

|
图 6 小波重构信号波形 Figure 6 Graphs of wavelet reconstruction |
采用均值滤波算法消除突发抖动干扰[15-16],在N长度光电容积脉搏波数字序列中,选择长度为n的序列Xn为一维模板窗口W(Nn),模板窗口数据由大到小排序成M序列,取序列中值M作为参考均值数值;顺次滑动模板窗口W(Nn),进行滤波,重复排序取中值过程,最终实现滤除扰动造成的噪声.
设采集获取的光电容积脉搏波时间序列X: Xin=x1, xi+1, xi+2,…,xi+n-1,i=0, 1, 2,…,N-n.一维模板窗口为:W(NKn)=W(Xin), K=0, 1, 2, …,N-1, i=0, 1, 2, …,N-n.均值提取: Mj=Med(sort(W(NKn))),j=0, 1, …,N-1.滤出漂移: Y=Xin-Mj, i=0, 1, …, N,j=0, 1, …, N-1.其基线及滤波结果如图 7所示.滤波处理后的频谱特性如图 8所示.

|
图 7 基线信号及去除基线漂移信号 Figure 7 Graphs of baseline signal and removal of baseline drift signal |

|
图 8 滤波后频谱图 Figure 8 Graphs of filtered frequency spectrogram |
实验获得效果采用信噪比和均方误差作为评价手段,信噪比SNR计算公式和均方误差RMSE计算公式为:
| $ SNR = 10\log \frac{{\sum\limits_{n = 1}^N {f{{\left( n \right)}^2}} }}{{\sum\limits_{n = 1}^N {{{\left[{f\left( n \right)-\hat f\left( n \right)} \right]}^2}} }}RMSE = \sqrt {\frac{{\sum\limits_{n = 1}^N {{{\left[{f\left( n \right)-\hat f\left( n \right)} \right]}^2}} }}{N}} . $ |
分别采用db3小波、db9小波、coif3小波和Haar小波进行消噪处理,获得的信噪比SNR和均方误差RMSE如表 1所示.
|
|
表 1 信噪比和均方误差测量值 Table 1 SNR and RMSE |
由表 1可知,采用Sym8小波函数分解,重构实现肝储备功能测量系统中的光电容积脉搏波信号的消噪滤波效果较好.
3 结语Sym8小波函数作为近似对称的紧支集双正交小波,具有优秀的信号时-频域分析特性,采用Sym8小波函数结合均值滤波算法对肝储备功能光电容积波信号滤波处理,有效地消除了噪声干扰,与传统的滤波消噪算法相比,其消噪效果更加有效,满足检测要求,对肝储备功能的无创精确检测提供了帮助.
| [1] |
IIJIMA T, AOYAGI T, IWAO Y, et al. Cardiac output and circulating blood volume analysis by pulse dye-densitometry[J]. Journal of clinical monitoring, 1997, 13(2): 87-89. (  0) 0) |
| [2] |
OKOCHI, OKOCHI O, KANEKO T, et al. ICG pulse spectrophotometry for perioperative liver function in hepatectomy[J]. Journal of surgical research, 2002, 103(1): 109-113. DOI:10.1006/jsre.2001.6328 (  0) 0) |
| [3] |
李宝亮, 穆毅, 蒋力, 等. Child-Pugh分级联合ICG与肝瞬时弹性值评估肝部分切除术肝细胞癌患者肝储备功能[J]. 中国肝脏病杂志(电子版), 2013, 5(3): 5-8. (  0) 0) |
| [4] |
张晓枫, 刘光达, 辛桂杰, 等. 结合近红外光谱法的肝血流参数测量[J]. 光学精密工程, 2012, 20(10): 2140-2146. (  0) 0) |
| [5] |
齐蓓蓓, 吴效明, 黄岳山. 基于MATALAB的脉搏波信号的实时处理[J]. 微计算机信息, 2009, 25(10): 184-185. (  0) 0) |
| [6] |
董锋. 基于脉搏波特征的连续血压测量方法研究[D]. 昆明: 云南大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10673-1015607812.htm
(  0) 0) |
| [7] |
陈雪峰. 脉搏波特征提取算法及其应用研究[D]. 大连: 大连理工大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10141-2006067923.htm
(  0) 0) |
| [8] |
刘光达, 黄敬涛, 卢蒙蒙, 等. 无创检测肝储备功能的脉搏色素密度法[J]. 吉林大学学报(工学版), 2012, 43(5): 1427-1432. (  0) 0) |
| [9] |
ZHA Y T, LIU G D, ZHOU R D. EEMD-ICA applied in signal extraction in functional near-infrared spectroscopy[J]. Spectroscopy and spectral analysis, 2015, 35(10): 2746-2751. (  0) 0) |
| [10] |
孔玲军. MATLAB小波分析超级学习手册[M]. 北京: 人民邮电出版社, 2014.
(  0) 0) |
| [11] |
李苗苗. 基于小波去噪的微型脉搏波监测仪[D]. 广州: 广东工业大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-11911-1012362529.htm
(  0) 0) |
| [12] |
RUHI M, BASHIR I M. Unsupervised eye blink artifact denoising of EEG data with modified multiscale sample entropy, kurtosis, and wavelet-ICA[J]. Biomedical and informatics, 2015, 19(1): 2168-2194. (  0) 0) |
| [13] |
朱玉清, 卫艳荣, 程正兴. 具有整数伸缩因子的多变量向量值双正交多小波包[J]. 郑州大学学报(理学版), 2012, 44(3): 61-65. (  0) 0) |
| [14] |
TEMESGHEN T, NOURHAN B, HANI S, et al. Adaptive ECG interval extraction[C]//IEEE International Symposium on Circuits and Systems, ISCAS. Portugal, 2015: 998-1001.
(  0) 0) |
| [15] |
DAS A B, BHUIYAN M I H, ALAM S M S. Classification of EEG signals using normal inverse Gaussian parameters in the dual-tree complex wavelet transform domain for seizure detection[J]. Signal, image and processing, 2016, 10(2): 259-266. DOI:10.1007/s11760-014-0736-2 (  0) 0) |
| [16] |
NAVARRO X, PORÉE F, BEUCHÉE A, et al. Denoising preterm EEG by signal decomposition and adaptive filtering: a comparative study[J]. Medical engineering and physics, 2015, 37(3): 315-320. DOI:10.1016/j.medengphy.2015.01.006 (  0) 0) |
| [17] |
CUI H L, LIU Y, YU M, et al. Application of wavelet denoising in distributed optical fiber interferometric vibration detection and location system[J]. Optics and engineering, 2015, 23(10z): 71-76. (  0) 0) |
| [18] |
ZENG K H, HUANG J, ZHEN T, et al. White noise energy and SNR estimation based on Haar wavelet decomposition for heart sound and electrocardiogram signals[J]. Lecture notes in electrical engineering, 2014, 309(1): 589-594. (  0) 0) |
 2017, Vol. 49
2017, Vol. 49


