2. 广西财经学院 信息与统计学院 广西 南宁 530003
2. School of Information and Statisitics, Guangxi University of Finance and Economics, Nanning 530004, China
从计算复杂性上分析,优化下料问题属于具有较高复杂性的NP-Hard问题[1],常见的优化算法主要有遗传算法、启发式算法、蚂蚁算法、模拟退火算法和混合算法等。在实际工程应用领域中,大规模、多尺寸的矩形件优化下料问题广泛出现于皮革套裁、金属板材切割、木材冲压等制造过程中。生成排样方式时考虑切割成本可以降低生产总成本[2]。综合考虑材料利用率高以及切割加工路径短两大优化目标对矩形件的生产加工具有重大的实际应用价值[3]。
目前,已有众多学者对大规模、多尺寸矩形件优化问题进行研究。文献[4]提出一种支持一刀切工艺约束的放宽式搜索算法。文献[5]采用蚁群算法解决大规模矩形件排样问题。文献[6]针对大规模矩形件正交排样问题,提出一种快速高效的启发式排放算法。文献[7]提出优化二叉树的启发式算法。文献[8]提出一种解决大规模二维剪切下料问题的有效方法。文献[9]采用遗传算法对大规模矩形零件优化套排。文献[10]针对大规模下料问题,提出基于零件相似性特征的分组优化方法。以上文献均只考虑提高材料利用率为优化目标。文献[11]提出大规模二维下料问题的禁忌搜索算法。文献[12]提出基于下料特征的大规模零件分组优化方法,考虑缓解排样算法在时间效率和材料利用率上的矛盾。上述文献均未考虑切割成本。
也有一些学者研究此类问题,且研究目标与本文相同,即以材料成本与切割成本总和最小为优化目标。文献[3, 13]提出一种面向可加工性的矩形件优化下料方法,构建条带的共边排样,且条带内相邻矩形件采用共边切割策略对切割路径进行优化。以上两篇文献采用激光切割工艺而均未考虑一刀切工艺,且只考虑了条带间相邻矩形件的共边切割,而本文在此基础上进一步优化,考虑条带内矩形件间的共边切割的同时,也考虑同质块内条带间的共边切割,充分发挥了共边切割的潜能,以尽可能地减少共边的重复切割,从而降低切割成本。文献[2]提出在生成三阶段排样方式时减少切割次数。尽管与文献[3]和[13]的优化目标相同,但切割工艺不同,因此文献的优化策略和方法均不适合于本文研究的问题。
文献[14]采用基于动态规划算法生成T形排样方式。文献[15]采用两阶段排样方式以简化工艺。均以排样方式中所含毛坯价值与切割成本之差最大为优化目标。以上文献均为解决无约束的矩形件下料问题,不适合解决本文研究的问题。
本文研究大规模、多尺寸矩形件优化下料问题,主要包括三方面内容:1) 同时考虑材料成本与切割成本,使用SVC算法生成多样性的下料方案,使用递归算法生成T形排样方式。2) 生成排样方式时,优先对大矩形件进行组合优化,该操作能有效跳出基于顺序法的局部最优的困境,从而提高材料利用率。3) 对含相同毛坯的同类型条带进行共边排样,组合成同质块,切割排样方式时充分考虑同质块内条带间以及矩形件间的共边切割,以减少切割成本。实验证明,本文算法在保证较高材料利用率的同时,能有效地减少切割加工次数。
1 数学模型及相关概念 1.1 问题描述及数学模型大规模、多尺寸(长×宽)的矩形件优化下料问题,即在n种尺寸为Lj×Wj,供应量为Dj(j=1, 2,…, n)的板材上切割出m种尺寸为li×wi,需求量和价值分别为di和vi(i=1, 2,…, m)的矩形件,优化目标为材料成本和切割成本总和最小。问题的解即为下料方案,一个下料方案由若干个排样方式组成。假设下料方案由K个排样方式,Z为材料成本和切割成本之和, ai为所含第i种矩形件的数量,Sk、Tk、u(k)和xk分别为第k个排样方式的面积、切割刀数、使用的板材号和使用次数,Z0+为非负整数,xk∈ Z0+,建立的整数规划模型如下:
| $ {\rm{min}}\;Z = \sum\limits_{k = 1}^K {({S_k} + \lambda {T_k}) \cdot {x_k}} {\rm{;}} $ | (1) |
| $ {\rm{s}}.\;{\rm{t}}.\;\;\sum\limits_{k = 1}^K {{a_i}\cdot{x_k} = {d_i}, i = 1, 2, \cdots , m} ; $ | (2) |
| $ \sum\limits_{k\backslash u\left( k \right) = j} {{x_k} \le {D_j}, j = 1, 2, \cdots , n} 。$ | (3) |
式(1)表示下料方案的优化目标是使消耗的材料成本和切割成本总和最小。λTk为切割成本,λ为控制参数,切割成本为下料过程中机床刀具、切割时长、机床刀具和能源等资源消耗通过λ以切割总刀数折算后得到。式(2)表示所有矩形件的需求必须满足。式(3)表示每种板材的使用次数不能超过其供应量。
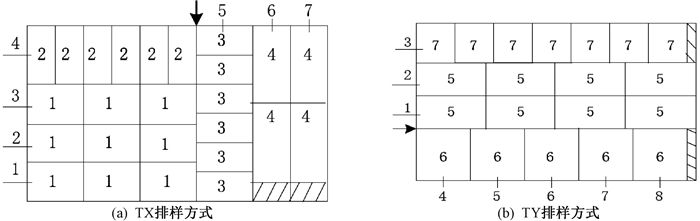
1.2 条带如图 1所示,本文采用T形排样方式,一条分界线把板材分成主辅2个段。图 1(a)为TX排样方式,主段在左,含水平条带,辅段在右,含竖直条带;图 1(b)为TY排样方式,主段在上,含水平条带,辅段在下,含竖直条带。分界线在板材边沿时,该排样方式是T形排样方式的特例。图形边上的数字用于标记条带,条带内的数字表示矩形件种类号,阴影部分表示余料。用X和Y分别标记水平方向和竖直方向,根据条带放置方向和矩形件放置方向,将条带分为XX(X条带,X矩形件)、XY(X条带,Y矩形件)、YX(Y条带,X矩形件)和YY(Y条带,Y矩形件)四种类型,在图 1(a)中,条带1~3为XX型,条带4为XY型,条带5为YX型,条带6~7为YY型。
|
图 1 2个T形排样方式示意图 Fig. 1 Two schematic diagrams of T pattern |
同质块是指由若干根包含同种矩形件且相邻的同类型条带组成的矩形。当同质块只包含一根同质条带时,同质块为一根条带,即同质块是同质条带的超集。如图 1(a)中,条带1~3组成一个同质块,条带4和5分别为两个不同的同质块,条带6~7组成一个同质块。
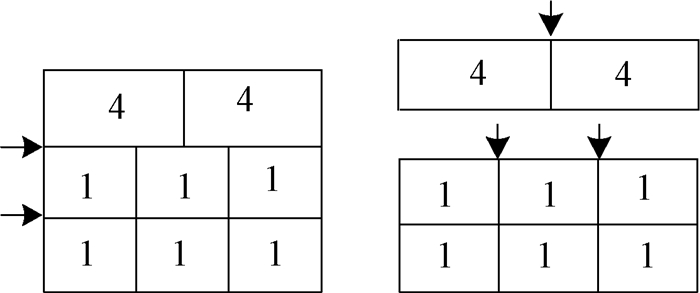
2 算法设计与实现 2.1 切割刀数优化方法生成排样方式时,算法在保证高材料利用率的同时,优先生成同质块,同质块间以“直线型”进行切割,综合考虑同质块条带间以及矩形件间的共边切割,提高加工效率。假设图 2为考虑生成同质块的T形排样方式的一个段及其切割示意图。其切割刀数为7。
|
图 2 切割示意图 Fig. 2 Schematic diagrams of cutting |
假设同质块内有γ根条带,且所有条带中最多含第i种矩形件的有效个数为ai,则该同质块切割刀数T的计算如下。
| $ 同质块条带内有余料时{\rm{:}}T = \left( {r - 1} \right) + {a_i}{\rm{;}} $ | (4) |
| $ 同质块条带内无余料时{\rm{:}}T{\rm{ = }}\left( {r - 1} \right) + \left( {{a_i} - 1} \right)。$ | (5) |
假设在TX形排样方式中待排样的板材,其主段和辅段的尺寸分别为L×W、x×W和(L-x)×W,矩形件的剩余需求为ri,分别用VXX(i, x)、VXY(i, x)、VYX(i, y)和VYY(i, y)表示四种尺寸分别为x×wi、x×li、y×li和y×wi条带的价值,其值的计算方法如表 1所示。TY形排样方式中各类型条带的价值可类似确定。
|
|
表 1 条带价值计算方法 Tab. 1 Strip value calculation method |
假设在尺寸为x×W的主段(其待排样方式尺寸为L×W)上生成X条带,最大价值为FX(x, W),则有
| $ {F_X}\left( {x, W} \right) = \left\{ \begin{array}{l} {\rm{max}}[{V_{XX}}\left( {i, x} \right) + {F_X}(x, W - {w_i})], \;\;\;\;当x \ge {l_i}且W \ge {w_i}时, \\ {\rm{max}}[{V_{XY}}\left( {i, x} \right) + {F_X}(x, W - {l_i})], \;\;\;\;\;\;当x \ge {w_i}且W \ge {l_i}时, \\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他。\end{array} \right. $ |
设递归函数Xseg(x, W)为返回主段x×W(x为水平边长度)的最大价值,其步骤如下。
1) 令FX(x, W)=0,i=1。
2) 如果x≥li且W≥wi,那么V=VXX(i, x)+Xseg(x, W-wi);如果x≥wi且W≥li,那么V=min{V, VXY(i, x)+Xseg(x, W-li)},
3) 如果FX(x, W) < V,令FX(x, W)=V,i=i+1。如果i≤m,转2);否则转4)。
4) 返回FX(x, W)。
设递归函数Yseg(W, L-x)返回辅段W×(L-x)上(W为竖直边长度)的最大价值为FY(W, L-x),其步骤可同理确定。
2.4 确定T形排样方式的递归算法对于TX形排样方式,设VTX为其价值,x为主段的长,L-x为辅段的长。设TXpat()函数用于确定TX排样方式,其步骤如下。
1) 令i=1,VTX=x=x0=0。
2) 如果x0>L,转4);否则转3)。
3) V=Xseg(x0, W)+Yseg(W, L-x0)-λTX,其中TX为TX形排样方式总切割刀数。如果V≤VTX,转2);否则,令VTX=V,x=x0,x0=x0+1,转2)。
4) 返回VTX。
设用TYpat()函数用于确定TY形排样方式,其步骤可同理确定。
确定T形排样方式的价值为max{TXpat(), TYpat()},取价值较大的排样方式作为T形排样方式。
2.5 确定下料方案设G为当前迭代次数,Gmax为最高迭代次数。SVC算法的步骤如下。
1) 令G=1,输入矩形件和板材的数据,初始化每种矩形件的价值等于其面积,即vi=li·wi,i=1, 2,…, m,并按照其价值大小相应增大其值vi=(vi/pp)>1且p < (li·wi),令矩形件的剩余需求ri=di,最好的下料方案总成本设为正无穷大。
2) 如果G=Gmax,则转7);
3) 确定排样方式(见2.4节)及其使用的板材号g和使用次数f(f=min{min(ri/zi),Dg|zi>0}),其中ai为当前排样方式所含第i种矩形件的个数,i=1, …, m。
4) 将当前排样方式加入下料方案,令ri=ri-xi ·f以修正矩形件的剩余需求,xi为当前排样方式含第i种矩形件的个数;令Dg=Dg-f以更新板材剩余供应量。
5) 如果仍有剩余矩形件需求,即
6) 如果当前下料方案的总成本小于最好下料方案总成本,则将当前排样方案记为最好下料方案,G=G+1,转2)。
7) 输出最好的下料方案。
为了保证全局最优,1)中,本文算法按照矩形件面积的大小相应地增大其价值,该操作使大的矩形件被优先排样,再在剩余的空闲区域排样小矩形件,能有效跳出基于顺序法的局部最优困境,从而提高材料利用率,本文取p=100。
3 实例结果与分析 3.1 与已发表文献算法比较采用文献[2]的4组实例数据,毛坯类型种数分别为5、10、20和40,每个组包含10个实例,每个实例的板材尺寸范围是L∈[2 000, 3 000],W∈[1 000, 1 500],毛坯的需求量在[100, 1 000]范围内均匀分布,这些均为工业中常见的尺寸。允许毛坯转向,允许生成TX排样方式和TY排样方式。将本文算法与文献[2]算法进行比较,表 2为实验结果,t1、u1和N1分别表示使用本文算法得出的每组实例的平均运行时间、材料利用率以及切割刀数,t2、u2和N2分别表示使用文献[2]算法得出的每组实例的平均运行时间、材料利用率以及切割刀数。本文设置λ=Sk/1 000(即当前排样方式所使用板材面积的1/1 000)。
|
|
表 2 实验结果 Tab. 2 The experiment results |
从表 2可以得出:本文算法的4组利用率比文献[2]算法平均高7.06%,较优的计算结果用加粗字体显示。本文算法的4组切割刀数比文献[2]算法平均减少5 018.5。虽然计算时间略长于文献[2]算法,但本文算法运行时间能满足实际应用需求。
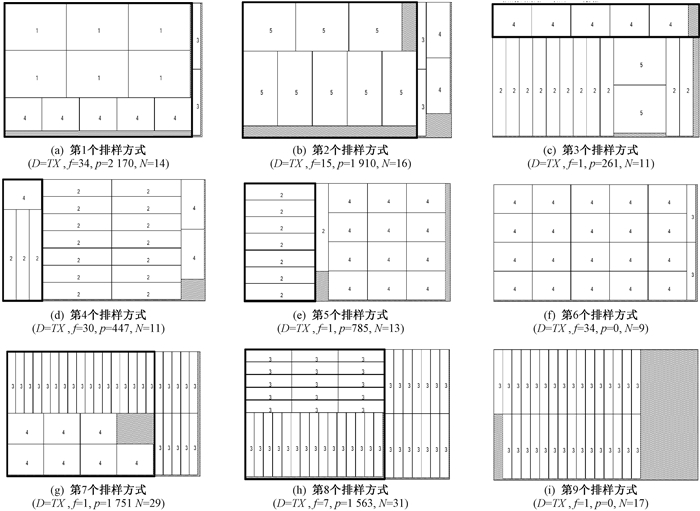
表 3为第1组例题7的板材和矩形件实例数据,矩形件总需求面积为284 699 049 mm2,板材尺寸为2 288 mm×1 054 mm,供应量充足。给出本文算法生成的第1组例题7的下料方案(见图 3),其中D=TX表示TX排样方式,D=TY表示TY排样方式,N、p和f分别为当前排样方式的切割刀数、分界线位置和使用次数。板材的总消耗面积为299 032 448 mm2,利用率为95.21%。切割总刀数为1 639。
|
|
表 3 第1组例题7的实例数据 Tab. 3 Example data of the first set of example 7 |
|
图 3 第1组实例7的下料方案 Fig. 3 The cutting plan for example 7 of the first set |
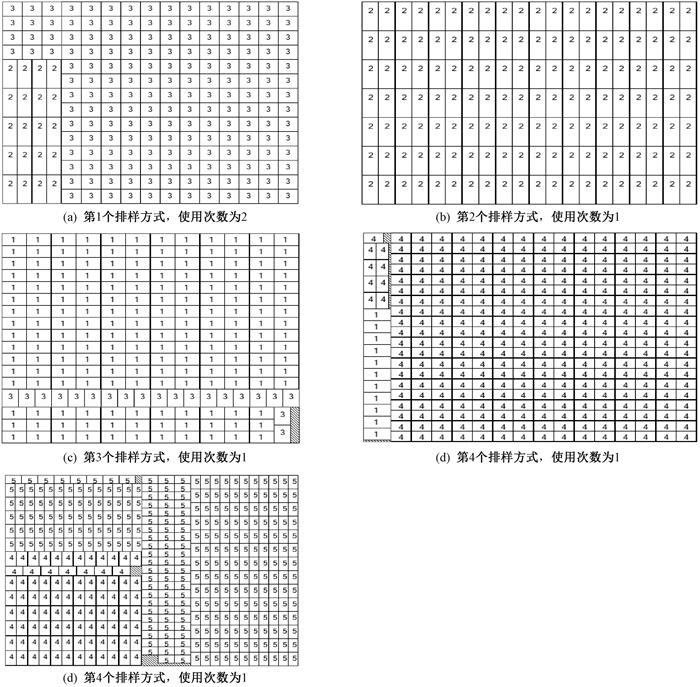
某工厂需要用规格1 800 mm×1 400 mm的板材,切割出5种矩形件毛坯,其毛坯具体数据见表 4, 该矩形件毛坯的总面积为15 080 000 mm2。图 4为其下料方案,共消耗板材6张,消耗板材总面积为15 120 000 mm2。材料利用率为99.74%。
|
|
表 4 毛坯尺寸及需求量 Tab. 4 Item size and demand |
|
图 4 一个生产实例的解 Fig. 4 A solution to a production instance |
本文针对制造业中大规模、多尺寸的矩形件优化下料问题,提出一种可加工性矩形件优化下料方法。同时兼顾考虑材料成本与切割成本,使用递归算法生成由2个段组成的T形排样方式,每个段均满足一刀切工艺约束,其切割工艺简单,有实际应用价值。生成排样方式时,优先对大矩形件进行组合优化,能有效跳出基于顺序法的局部最优的困境,从而减少材料成本。对含相同毛坯的同类型条带进行共边排样,组成同质块。切割排样方式时充分考虑同质块内条带间以及矩形件间的共边切割,进而提高切割效率。通过与其他文献算法比较证明了本文所提方法在保证较高材料利用率的同时,能有效减少切割刀数。
在此基础上,笔者基于本文方法设计了可应用于实践的下料系统,且该系统取得了较好的应用效果。后续将会对时间优化进行进一步研究。
| [1] |
贾志欣. 排样问题的研究现状与趋势[J]. 计算机辅助设计与图形学学报, 2004, 16(7): 890-897. JIA Z X. State-of-the-art and future trends of cutting and packing studies[J]. Journal of computer aided design & computer graphics, 2004, 16(7): 890-897. DOI:10.3321/j.issn:1003-9775.2004.07.003 (  0) 0) |
| [2] |
CUI Y D, HUANG B X. Reducing the number of cuts in generating three-staged cutting patterns[J]. European journal of operational research, 2012, 218(2): 358-365. DOI:10.1016/j.ejor.2011.10.047 (  0) 0) |
| [3] |
吴电建, 阎春平, 李俊, 等. 面向可加工性的矩形件优化下料方法[J]. 计算机集成制造系统, 2018, 24(6): 1374-1382. WU D J, YAN C P, LI J, et al. Manufacturability-oriented rectangular parts cutting stock method[J]. Computer integrated manufacturing systems, 2018, 24(6): 1374-1382. (  0) 0) |
| [4] |
张帆, 刘强, 张浩, 等. 面向多规格板材的矩形工件排样优化方法[J]. 计算机集成制造系统, 2015, 21(11): 2921-2928. ZHANG F, LIU Q, ZHANG H, et al. Packing optimization of rectangle workpieces oriented to variable-sized bin[J]. Computer integrated manufacturing systems, 2015, 21(11): 2921-2928. (  0) 0) |
| [5] |
郭怡, 李辉. 基于蚁群算法的矩形件排样问题研究[J]. 中国农机化学报, 2014, 35(4): 250-252, 256. GUO Y, LI H. Research on rectangular packing problem based on ant colony algorithm[J]. Journal of Chinese agricultural mechanization, 2014, 35(4): 250-252, 256. (  0) 0) |
| [6] |
陈仕军, 曹炬. 矩形件优化排样的一种启发式算法[J]. 计算机工程与应用, 2010, 46(12): 230-232, 238. CHEN S J, CAO J. Heuristic algorithm for rectangular cutting stock problem[J]. Computer engineering and applications, 2010, 46(12): 230-232, 238. (  0) 0) |
| [7] |
戈鹏, 邱厌庆, 刘柱胜, 等. 一刀切问题的优化二叉树排样[J]. 计算机集成制造系统, 2011, 17(2): 329-337. GE P, QIU Y Q, LIU Z S, et al. Optimized binary tree packing of guillotine problem[J]. Computer integrated manufacturing systems, 2011, 17(2): 329-337. (  0) 0) |
| [8] |
FAYARD D, HIFI M, ZISSIMOPOULOS V. An efficient approach for large-scale two-dimensional guillotine cutting stock problems[J]. Journal of the operational research society, 1998, 49(12): 1270-1277. DOI:10.1057/palgrave.jors.2600638 (  0) 0) |
| [9] |
杨威, 罗阳, 刘胜青. 大规模矩形零件优化套排的遗传算法[J]. 四川大学学报(工程科学版), 2001, 33(5): 59-62. YANG W, LUO Y, LIU S Q. Genetic algorithm for large scale rectangular object optimal embed placement[J]. Journal of Sichuan university (engineering science edition), 2001, 33(5): 59-62. (  0) 0) |
| [10] |
尹震飚, 阎春平, 刘飞, 等. 基于零件相似性特征的大规模下料分组优化方法[J]. 计算机辅助设计与图形学学报, 2007, 19(11): 1442-1446. YIN Z B, YAN C P, LIU F, et al. A grouping optimization method for solving large-scale cutting stock problem based on the similarity of parts[J]. Journal of computer-aided design & computer graphics, 2007, 19(11): 1442-1446. (  0) 0) |
| [11] |
ALVAREZ-VALDÉS R, PARAJÓN A, TAMARIT J M. A tabu search algorithm for large-scale guillotine (un)constrained two-dimensional cutting problems[J]. Computers & operations research, 2002, 29(7): 925-947. (  0) 0) |
| [12] |
覃斌, 阎春平, 汪科, 等. 基于下料特征的大规模零件分组优化方法[J]. 计算机辅助设计与图形学学报, 2012, 24(3): 387-393. QIN B, YAN C P, WANG K, et al. Grouping optimization method of large-scale parts based on cutting stock characteristics[J]. Journal of computer-aided design & computer graphics, 2012, 24(3): 387-393. DOI:10.3969/j.issn.1003-9775.2012.03.015 (  0) 0) |
| [13] |
鲁淑飞, 陈燕, 崔耀东. 面向可加工性的矩形件优化下料算法[J]. 计算机工程与应用, 2020, 56(17): 55-59. LU S F, CHEN Y, CUI Y D. Machinability-oriented optimization algorithm for rectangular items cutting stock problem[J]. Computer engineering and applications, 2020, 56(17): 55-59. (  0) 0) |
| [14] |
李秋蓉, 崔耀东, 罗丹. 考虑切割刀数的T形排样算法研究[J]. 计算机应用与软件, 2013, 30(3): 28-29, 138. LI Q R, CUI Y D, LUO D. Research on the algorithm of T-shape cutting patterns with cuts number consideration[J]. Computer applications and software, 2013, 30(3): 28-29, 138. (  0) 0) |
| [15] |
潘卫平, 陈秋莲, 崔耀东. 考虑切割刀数的最优两段排样算法研究[J]. 广西大学学报(自然科学版), 2014, 39(3): 687-692. PAN W P, CHEN Q L, CUI Y D. Research on the algorithm for generating optimal two segment cutting patterns with cuts number consideration[J]. Journal of Guangxi university (natural science edition), 2014, 39(3): 687-692. (  0) 0) |
 2021, Vol. 53
2021, Vol. 53


