非线性发展方程可以用来描述等离子体物理、非线性光学、流体力学等许多物理现象。为了更好地理解这些物理现象的本质,寻找非线性发展方程的相关解就显得尤为重要。文献[1]通过Painlevé截断展开法提出了留数对称定理。同时,为了得到更多非线性系统的本质特征,文献[2]提出了一致的Riccati展开(CRE)法,在此基础上,不仅可以明确非线性系统的可积性,还可以构造孤子与其他多种非线性波之间的相互作用解[3-5]。本文主要对修正Broer-Kaup-Kupershmidt(MBKK)方程[6]
| $ \left\{ {\begin{array}{*{20}{l}} {{u_t} = - \frac{1}{2}{u_{xx}} - 2u{u_x} + \frac{1}{2}{v_{xx}}, }\\ {{v_t} = \frac{1}{2}{v_{xx}} - 2{{(uv)}_x}} \end{array}} \right. $ | (1) |
进行了研究。MBKK方程是由(2+1)维BKK方程[7]当y=x时改写得到的。BKK方程是描述非线性和色散长重力波在浅海水平方向均匀深度的模型, MBKK方程则主要用于描述浅水波的运动。目前, 已有文献主要针对BKK方程进行研究, 而对MBKK方程的研究较少, 如文献[8]用Hirota方法把非线性方程化为双线性方程, 然后通过摄动法寻找其精确解。本文首先用Painlevé分析法[9]研究MBKK方程的留数对称和相应的有限变换,其次用CRE方法得到MBKK方程的新的相互作用解。
1 MBKK方程的非局域留数对称及其局域化由MBKK方程(1)的非线性项与色散项的平衡,可得其Painlevé截断展开[10]为
| $ \left\{ {\begin{array}{*{20}{l}} {u = \frac{{{u_1}}}{\phi } + {u_0}, }\\ {v = \frac{{{v_1}}}{\phi } + {v_0}, } \end{array}} \right. $ | (2) |
式中:u0、u1、v0、v1、均为x和t的函数。将方程(2)代入方程(1),取1/Φ的各次幂系数为0,可得
| $ {u_1} = - \frac{{{\phi _x}}}{4};{v_1} = - \frac{{3{\phi _x}}}{8};{u_0} = \frac{{{\phi _{xx}} - 4{\phi _t}}}{{8{\phi _x}}};{v_0} = \frac{{3{\phi _{xx}}}}{{16{\phi _x}}}。$ | (3) |
Φ满足方程(1)的Schwartzian形式,即
| $ 2{C_{xx}} - {S_x} = 0, $ | (4) |
式中:
方程(4)在Möbious变化
| $ \phi \to \frac{{a + b\phi }}{{c + d\phi }}, (ad \ne bc) $ | (5) |
下保持不变,这表示方程(4)拥有σΦ=a、σΦ=b和σΦ=c2三种对称,将方程(2)代入方程(1),可得定理1。
定理1(Bäcklund变换定理) 若Φ是方程(4)的解,则
| $ \left\{ {\begin{array}{*{20}{l}} {u = \frac{{{\phi _{xx}} - 4{\phi _t}}}{{8{\phi _x}}}, }\\ {v = \frac{{3{\phi _{xx}}}}{{16{\phi _x}}}} \end{array}} \right. $ | (6) |
是方程(1)关于Φ和解u, v间的一个Bäcklund变换。当Φ和解u, v满足Bäcklund变换(6)时,方程(1)有如下留数对称:
为了将留数对称局域化[11],引入辅助变量g=g(x, t),利用表达式
| $ g = {\phi _x}, $ | (7) |
则方程(1)的非局域留数对称被局域化为延拓系统(1)、(6)、(7)的Lie点对称,即
| $ {\sigma ^u} = - \frac{1}{4}g;{\sigma ^v} = - \frac{3}{8}g;{\sigma ^g} = - 2\phi g;{\sigma ^\phi } = - {\phi ^2}。$ | (8) |
相应的Lie点对称的向量场表达式为
| $ V = - \frac{1}{4}g{\partial _u} - \frac{3}{8}g{\partial _v} - 2\phi g{\partial _g} - {\phi ^2}{\partial _\phi }。$ | (9) |
由Lie的第一基本定理,解如下的初值问题:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}\hat u(\varepsilon )}}{{{\rm{d}}\varepsilon }} = - \frac{1}{4}\hat g(\varepsilon ), \hat u(0) = u, }\\ {\frac{{{\rm{d}}\hat v(\varepsilon )}}{{{\rm{d}}\varepsilon }} = - \frac{3}{8}\hat g(\varepsilon ), \hat v(0) = v, }\\ {\frac{{{\rm{d}}g(\varepsilon )}}{{{\rm{d}}\varepsilon }} = - 2(\hat \phi (\varepsilon )\hat g(\varepsilon )), \hat g(0) = g, }\\ {\frac{{{\rm{d}}\hat \phi (\varepsilon )}}{{{\rm{d}}\varepsilon }} = - \hat \phi {{(\varepsilon )}^2}, \hat \phi (0) = \phi }。\end{array}} \right. $ | (10) |
可得Lie点对称(9)的有限对称变换为
| $ \left\{ {\begin{array}{*{20}{l}} {\hat u(\varepsilon ) = u - \frac{{g\varepsilon }}{{4(\varepsilon \phi + 1)}}, }\\ {\hat v(\varepsilon ) = v - \frac{{3g\varepsilon }}{{8(\varepsilon \phi + 1)}}, }\\ {\hat g(\varepsilon ) = \frac{g}{{{{(\varepsilon \phi + 1)}^2}}}, }\\ {\hat \phi (\varepsilon ) = \frac{\phi }{{\varepsilon \phi + 1}}, } \end{array}} \right. $ | (11) |
式中:ε是任意群参数。
2 MBKK方程的CRE可解与新的精确解根据CRE方法[12],方程(1)有如下的截断展开式:
| $ {\left\{ {\begin{array}{*{20}{l}} {u = {u_0} + \frac{{{u_1}}}{{R(\omega )}}, }\\ {v = {v_0} + \frac{{{v_1}}}{{R(\omega )}}, } \end{array}} \right.} $ | (12) |
式中:ω=ω(x, t);R(ω)是Riccati方程
| $ {{R_\omega } = {l_0} + {l_1}R + {l_2}{R^2}} $ | (13) |
的解, l0、l1、l2为任意常数, R=R(ω)。
将式(12)和(13)代入方程(1), 并令
| $ {u_1} = - \frac{{{\omega _x}{l_0}}}{4}, {u_0} = - \frac{{\omega _x^2{l_1} - {\omega _{xx}} + 4{\omega _t}}}{{8{\omega _x}}}, {v_1} = - \frac{{3{\omega _x}{l_0}}}{8}, {v_0} = - \frac{{3\omega _x^2{l_1} - 3{\omega _x}}}{{16{\omega _x}}}, $ |
且ω满足方程
| $ \frac{{3\delta }}{{32}}{\omega _x}{\omega _{xx}} - \frac{3}{{32}}{S_x} + \frac{3}{{16}}{C_{xx}} = 0, $ | (14) |
式中:
为求相互作用解,可设相容性方程(14)的解的具体形式为
| $ \omega = {k_1}x + {p_1}t + W(X);X = {k_2}x + {p_2}t。$ | (15) |
将式(15)代入式(14),得到椭圆方程
| $ W_{1X}^2 = {C_0} + {C_1}{W_1} + {C_2}W_1^2 + {C_3}W_1^3 + {C_4}W_1^4, $ | (16) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{C_0} = \frac{{k_1^2(4k_1^2{l_0}{l_2} - k_1^2l_1^2 + {C_2}k_2^2)}}{{3k_2^4}}, }\\ {{C_1} = \frac{{{k_1}(4k_1^2{l_0}{l_2} - k_1^2l_1^2 + {C_2}k_2^2)}}{{k_2^3}}, }\\ {{C_3} = \frac{{ - 20k_1^2{l_0}{l_2} + 5k_1^2l_1^2 + {C_2}k_2^2}}{{3{k_1}{k_2}}}, }\\ {{C_4} = \delta , {p_1} = \frac{{{p_2}{k_1}}}{{{k_2}}}, {W_1}(X) = {W_X}, } \end{array}} \right. $ | (17) |
其中C2, k1, k2, p2为任意常数。则MBKK方程(1)的解有如下形式:
| $ \left\{ {\begin{array}{*{20}{l}} {u = - \frac{{{l_1}{{({k_1} + {k_2}{W_X})}^2} - k_2^2{W_{XX}} + 4({p_1} + {p_2}{W_X})}}{{8({k_1} + {k_2}{W_X})}} - \frac{{{l_0}({k_1} + {k_2}{W_X})}}{{4R(\omega )}}, }\\ {v = - \frac{{3({l_1}{{({k_1} + {k_2}{W_X})}^2} - k_2^2{W_{XX}})}}{{16({k_1} + {k_2}{W_X})}} - \frac{{3{l_0}({k_1} + {k_2}{W_X})}}{{8R(\omega )}}}。\end{array}} \right. $ | (18) |
下面通过2个例子来具体给出MBKK方程的孤立波与椭圆周期波之间的相互作用解。
例1 取椭圆函数方程(16)的解为
| $ W = c{E_\pi }( sn ({k_2}x + {p_2}t, m), n, m), $ | (19) |
式中:sn(q, m)为椭圆函数;Eπ为第三类不完全椭圆积分。取l0=-1, l1=0, l2=-1, 此时Riccati方程的解为R(ω)=cot(ω)。
将R(ω)=cot(ω)和式(19)代入式(18),可得MBKK方程的相互作用解为
| $ u = \frac{{4{p_1} + \frac{{4c{p_2}}}{{ - {S^2}n + 1}} - \frac{{2ck_2^2nSCD}}{{{{( - {S^2}n + 1)}^2}}}}}{{8({k_1} + \frac{{c{k_2}}}{{ - {S^2}n + 1}})}} + \frac{{{k_1} + \frac{{c{k_2}}}{{ - {S^2}n + 1}}}}{{4{\rm{cot}}({k_1}x + {p_1}t + c{E_\pi }(S, n, m))}}, $ |
| $ v = \frac{{3ck_2^2nSCD}}{{8({k_1} + \frac{{c{k_2}}}{{ - {S^2}n + 1}}){{( - {S^2}n + 1)}^2}}} + \frac{{3({k_1} + \frac{{c{k_2}}}{{ - {S^2}n + 1}})}}{{8{\rm{cot}}({k_1}x + {p_1}t + c{E_\pi }(S, n, m))}}, $ |
式中:S=sn(k2x+p2t, m);C=cn(k2x+p2t, m);D=dn(k2x+p2t, m)。
将式(15)和式(19)代入方程(14),利用Maple软件解超定方程可得:c、m、k1、k2、p1、p2为任意常数,n=0。
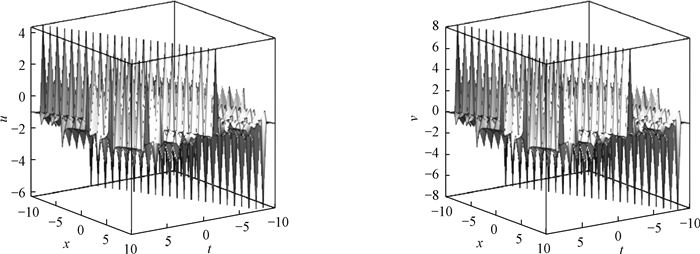
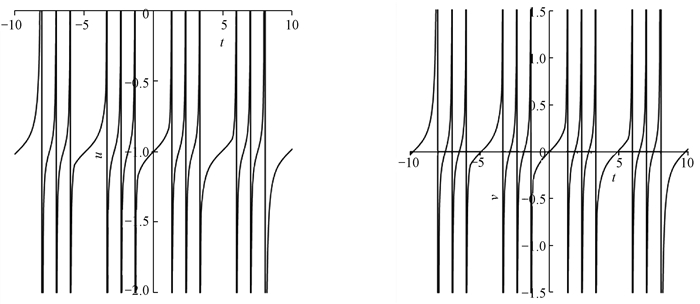
图 1为例1中u, v相互作用解的波形图, 图 2为x=0时u, v的平面周期波解结构。参数选择如下:{c=-0.553 931 451 6, m=0.9, n=0, k1=1, k2=1, p1=2, p2=2}。可以看出, 解u, v分别具有多个不在同一平面上的波峰和波谷,且这些波峰和波谷的凹陷程度不同。
|
图 1 例1中u, v相互作用解的波形图 Fig. 1 Waveform of the solutions of u and v in sample 1 |
|
图 2 例1中x=0时u, v的平面周期波解结构 Fig. 2 The structure of plane periodic wave solutions of u and v at x=0 in sample 1 |
例2
| $ \begin{array}{l} u = \frac{1}{{4({k_2}( - {S^2} + 1)( - {n^2}{S^2} + 1) - 2{S^2}{k_1} + 2{k_1})}}\left( {\left( {\frac{{k_2^2{{( - {n^2}{S^2} + 1)}^2}S}}{{2( - {S^2} + 1)}} + \frac{{k_2^2( - {S^2} + 1){n^2}S}}{2} - k_2^2{{( - {n^2}{S^2} + 1)}^2}S - } \right.} \right.\\ \left. {\left. {\frac{{2({p_2}( - {S^2} + 1)( - {n^2}{S^2} + 1) - 2{S^2}{p_1} + 2{p_1})}}{{{S^2} - 1}}} \right)({S^2} - 1)} \right), \end{array} $ |
| $ v = - \frac{{3( - \frac{{k_2^2{{( - {n^2}{S^2} + 1)}^2}S}}{{2( - {S^2} + 1)}} - \frac{{k_2^2( - {S^2} + 1){n^2}S}}{2} + k_2^2{{( - {n^2}{S^2} + 1)}^2}S)({S^2} - 1)}}{{8({k_2}( - {S^2} + 1)( - {n^2}{S^2} + 1) - 2{S^2}{k_1} + 2{k_1})}}, $ |
式中:
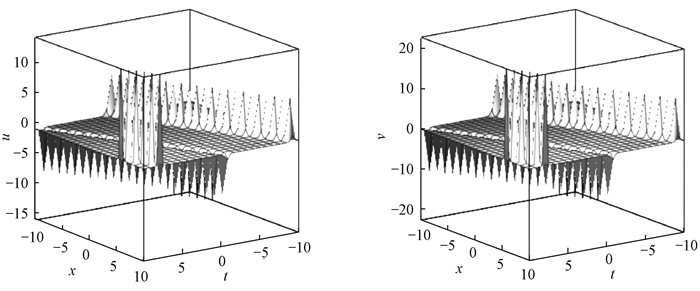
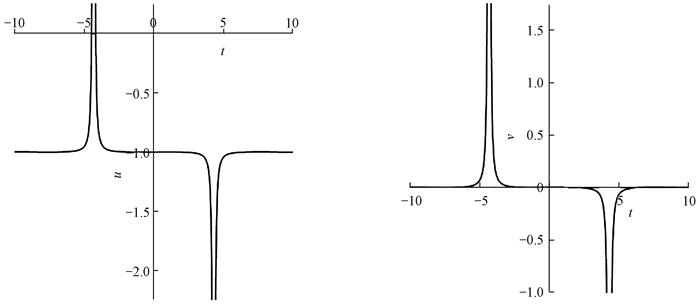
图 3为例2中u, v相互作用解的波形图, 图 4为x=0时u, v的平面周期波解结构。参数选择如下:{n=0.568, k1=0.4, k2=0.2, p1=0.8, p2=0.4}。可以看出,解u, v分别具有多个波峰和波谷,且波峰和波谷的凹陷程度不同。
|
图 3 例2中u, v相互作用解的波形图 Fig. 3 Waveform of the solutions of u and v in sample 2 |
|
图 4 例2中x=0时u, v的平面周期波解结构 Fig. 4 The structure of plane periodic wave solutions of u and v at x=0 in sample 2 |
由Painlevé截断展开法得到MBKK方程的留数对称, 并通过引入合适的新变元将其局域化为Lie点对称, 在此基础上, 利用Lie的第一基本定理研究了延拓系统的有限变换。最后, 用CRE方法获得了MBKK方程的相互作用解。为了更好地研究解的性质, 通过选取适当的参数, 给出了解的相应图形。
| [1] |
LOU S Y. Residual symmetries and Bäcklund transformations[EB/OL].[2019-10-01]. https://arxiv.org/abs/1308.1140.
(  0) 0) |
| [2] |
LOU S Y. Consistent Riccati expansion for integrable systems[J]. Studies in applied mathematics, 2015, 134(3): 372-402. DOI:10.1111/sapm.12072 (  0) 0) |
| [3] |
FENG L L, TIAN S F, ZHANG T T. Nonlocal symmetries and consistent Riccati expansions of the (2+1) -dimensional dispersive long wave equation[J]. Zeitschrift für naturforschung, 2017, 72(5): 425-431. DOI:10.1515/zna-2017-0012 (  0) 0) |
| [4] |
LI Y Y, HU H C. Nonlocal symmetries and interaction solutions of the Benjamin-Ono equation[J]. Applied mathematics letters, 2018, 75: 18-23. DOI:10.1016/j.aml.2017.06.012 (  0) 0) |
| [5] |
CHEN J C, MA Z Y. Consistent Riccati expansion solvability and soliton-cnoidal wave interaction solution of a (2+ 1) -dimensional Korteweg-de Vries equation[J]. Applied mathematics letters, 2017, 64: 87-93. DOI:10.1016/j.aml.2016.08.016 (  0) 0) |
| [6] |
BAI C L, ZHAO H. A new general algebraic method and its applications to the (2 + 1) -dimensional Broer-Kaup-Kupershmidt equations[J]. Applied mathematics and computation, 2010, 217(4): 1719-1732. DOI:10.1016/j.amc.2009.10.034 (  0) 0) |
| [7] |
TANG X Y, LOU S Y, ZHANG Y. Localized excitations in (2+1) -dimensional systems[J]. Physics review E, 2002, 66(4): 1-17. (  0) 0) |
| [8] |
孟祥德, 高建军, 杨瑞朋. (1 + 1)维修正Broer-Kaup-Kupershmidt方程的双线性化和精确解[J]. 洛阳师范学院学报, 2013, 32(8): 1-3. MENG X D, GAO J J, YANG R P. Double linearization and accurate solution of (1 + 1) dimension positive Broer-KaupKupershmidt equation[J]. Journal of Luoyang normal university, 2013, 32(8): 1-3. DOI:10.3969/j.issn.1009-4970.2013.08.001 (  0) 0) |
| [9] |
CONTO R. Invariant Painlevé analysis of partial differential equations[J]. Physics letters A, 1989, 140(7/8): 383-390. (  0) 0) |
| [10] |
PENG Y Z. A new (2+1) -dimensional KdV equation and its localized structures[J]. Communications in theoretical physics, 2010, 54(5): 863-865. DOI:10.1088/0253-6102/54/5/17 (  0) 0) |
| [11] |
XIA Y R, XIN X P, ZHANG S L. Residual symmetry, interaction solutions, interactions and conservation laws of the (2+1) -dimensional dispersive long-wave system[J]. Chinese physics B, 2017, 26(3): 030202. DOI:10.1088/1674-1056/26/3/030202 (  0) 0) |
| [12] |
SONG J F, HU Y H, MA Z Y. Bäcklund transformation and CRE solvability for the negative-order modified KdV equation[J]. Nonlinear dynamics, 2017, 90(1): 575-580. (  0) 0) |
 2020, Vol. 52
2020, Vol. 52


