0 引言

电力系统需要保持发电功率和用电负荷实时平衡.传统调度运行方式利用负荷预测数据调整发电输出功率实现系统的平衡.然而随着大量光伏发电接入电网后，光伏发电功率具有的随机性和波动性特点增加了系统实时平衡的难度，这就要求调度运行中需要进行光伏发电功率的预测^[1-2].只有进行了准确及时的光伏发电功率预测, 才能达到优化电网调度运行的目的^[3].

文献[4-6]采用基于BP神经网络的组合算法模型进行光伏发电功率预测，但BP神经网络的学习速率慢、可靠性受网络敏感参数影响较大，模型实用性有待考证.文献[7-8]采用基于标准PSO算法的组合算法模型进行光伏功率预测，优化过程缺乏搜索重点，不利于最优模型参数的搜寻.文献[9-10]采用智能群优化算法优化的ELM模型进行了短期负荷预测，预测结果显示, 经优化后的ELM性能要优于未经优化的单一ELM模型.结合光伏发电输出功率的特点，采用PSO与ELM相结合的算法模型有望进一步提高短期光伏发电功率预测的预测精度.

本文提出了一种基于PSO和ELM组合算法的短期光伏发电功率预测模型.模型利用PSO算法寻优优化的能力，通过调整PSO算法不同阶段的寻优重点，为ELM设定了最佳网络参数，避免了ELM随机产生输入层权值和隐含层阈值造成的光伏发电功率预测不稳定问题.而ELM的预测结果除了受网络连接参数影响外，还受隐含层节点数的影响.为了进一步提高预测结果的准确性，这里结合传统神经网络以及ELM网络隐含层节点的选取原则，为组合模型设定了最佳隐含层节点数，从而提高了模型的预测精度.采用光伏电站内的实际数据验证了组合算法模型能够有效提高短期光伏发电功率预测的预测精度.

1 相关性检验

数据间的相关性检验有助于网络模型排除不相关因素, 保留有效数据，降低数据冗余，提高模型预测的精度.实际中不仅存在着各影响因素同光伏发电功率间的关联关系，各影响因素间同样也存在着一定的内在联系.此时仅仅进行单一影响因素与功率间的相关性检验，可能无法有效判断数据的内在联系，故需要对检验方法进行改进，实现多影响因素同光伏发电功率间的组合检验.这里引入了计算修正RV系数的组合相关性检验法.修正RV系数也即RV_mod，是一种基于矩阵计算的相关性分析方法，是皮尔逊相关系数方式的重新构造，具有较强的泛化性^[11].两个矩阵 M 和N的修正RV系数计算过程为

$R{V_{{\rm{mod}}}} = \frac{{{\rm{tr}}(\mathit{\boldsymbol{MN}})}}{{\sqrt {{\rm{tr}}{{(\mathit{\boldsymbol{M}})}^2}{\rm{tr}}{{(\mathit{\boldsymbol{N}})}^2}} }}, $

(1)

其中：$\mathit{\boldsymbol{M}} = \mathit{\boldsymbol{J}}{\mathit{\boldsymbol{J}}^{\rm{T}}} - {\rm{diag}}\left( {\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{J}}^{\rm{T}}}} \right)$；$\mathit{\boldsymbol{N}} = \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{K}}^{\rm{T}}} - {\rm{diag}}\left( {\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right)$；J代表影响因素矩阵，包括有总辐射量、直射辐射、散射辐射、环境温度、气压、相对湿度以及组件温度；K 代表光伏输出功率矩阵；diag(·)为取出矩阵对角线元素的函数；tr(·)为矩阵的迹，即取矩阵主对角线元素和的函数.修正RV系数可以反映变量间的正相关与负相关，所以RV_mod∈[－1, 1].当RV_mod越接近-1或者1时，影响因素同输出功率之间的相互替换越合理.根据式(1)可以计算出不同影响因素组合后同输出功率间的修正RV系数，如表 1所示.

根据检验结果可知，总辐射量和直射辐射两个影响因素的组合同输出功率间的关联性最强.

2 算法简介 2.1 ELM网络简介

ELM是一种单隐含层前馈神经网络算法，具有适应性强、训练速度快的特点^[12]. ELM随机生成输入权值和隐含层节点数，所用公式^[13-18]为 Hβ = T^T, 其中：H 为网络隐含层输出矩阵；β 为输出层阈值矩阵；T 为网络的输出矩阵.

ELM网络在训练过程里输出矩阵 H 保持不变，β 能够利用式$\mathop {\min }\limits_\mathit{\boldsymbol{\beta }} \left\| {\mathit{\boldsymbol{H\beta }} - {\mathit{\boldsymbol{T}}^{\rm{T}}}} \right\|$的最小二乘解得到.所求解为$\mathit{\boldsymbol{\widehat \beta }} = {\mathit{\boldsymbol{H}}^ + }{\mathit{\boldsymbol{T}}^{\rm{T}}}$，H⁺是隐含层输出矩阵的穆尔-彭罗斯广义逆矩阵.

2.2 ELM网络隐含层节点设置

根据相关性检验结果可知，ELM的输入数据类型共有2个，故对应的网络输入节点数为2.其中网络输入节点1对应的是光伏场站的总辐射量，网络输入节点2对应的是光伏场站的直射辐射量.在ELM中对预测结果影响最大的就是隐含层节点数.传统神经网络最佳隐含层节点数设定原则^[19]为

$L < n - 1, L < \sqrt {(m + n)} + a, L = {\log _2}n, $

其中：L为隐含层节点数；n为输入节点数；a∈[0, 10]间的随机整数；m为输出节点数.结合传统神经网络隐含层神经元节点数可知，ELM隐含层节点数的选取范围在1至11之间.而ELM隐含层节点选取原则中，当预测样本数目较大时，为了减少计算量，隐含层节点数应不大于输入节点数2.

由以上分析可知，此次建模过程中ELM隐含层节点数最终范围确定在1和2之间.当隐含层节点数为1时，仿真实验得到预测结果的平均绝对误差和均方根误差分别为4.951 7和7.970 5；当隐含层节点数为2时，仿真实验得到预测结果的平均绝对误差和均方根误差分别为4.564 5和7.205 4.因此选取隐含层节点数为2时，ELM网络的预测精度较高.

2.3 PSO算法简介

PSO算法作为智能群优化算法的一种，其可用于优化问题的求解过程.待求解问题所有可行解的集合构成了解空间，粒子为解集合内的元素，粒子适应度值由算法适应度函数决定.通过比较粒子适应度值和两个极值来调整粒子的速度和位置，两个极值分别为个体极值和群体极值^[20].

寻优时粒子速度和位置更新为

$\begin{array}{*{20}{c}} {V_{id}^{k + 1} = \omega V_{id}^k + {c_1}{r_1}\left( {P_{id}^k - X_{id}^k} \right) + {c_2}{r_2}\left( {P_{gd}^k - X_{id}^k} \right);}\\ {X_{id}^{k + 1} = X_{id}^k + V_{id}^{k + 1}, } \end{array}$

(2)

式中：ω为惯性权重；d=1, 2, 3, …, m，i=1, 2, 3, …, n，m为解空间维数，n为粒子个数；k为当前迭代次数；c₁和c₂为加速因子；P_i和P_g分别为个体极值和群体极值；r₁和r₂为分布于[0, 1]之间随机数；X_id为粒子的位置；V_id为粒子的速度.PSO算法应用时，待优化的粒子为ELM输入层权值和隐含层阈值，适应度函数为ELM网络预测功率同实际输出功率间的均方误差.

2.4 PSO算法参数设置

采用PSO算法目的是利用其寻优优化的能力，在一定范围内搜索到ELM网络的最优网络连接参数，从而达到提高光伏功率预测精度的作用.能够有效改善寻优效果的几个重要参数的设置方法如下.

1) 惯性权重.更新速度时惯性权重ω反映了粒子继承先前速度的比重.较大的ω有利于全域寻优，而较小的ω有助于局域寻优，为了平衡算法的寻优过程，本文采用了线性递减惯性权重^[21].

其中ω_start、ω_end分别是初始寻优时、最大寻优次数时的权重，且当ω_start=0.4、ω_end=0.9时，寻优后ELM网络的光伏功率预测精度最高.

2) 加速因子.标准PSO算法中通常设置c₁=c₂, 使得粒子朝着两个不同的位置移动的概率相同，但没有考虑到各粒子在不同阶段的搜索重点^[22].对c₁和c₂做了相对非线性配对调整发现，c₁+c₂不大于3时最有利于ELM网络的光伏发电功率预测^[23].为了平衡搜索时粒子向群体极值位置和个体极值位置移动的概率，当k≤T_max/2时，令c₁=1.4，c₂=1.6；当k>T_max/2时，令c₁=1.6，c₂=1.4.

3) 粒子速度和位置.为避免粒子在优化时出现寻优发散的现象，一般要求将其速度和位置在一定空间内，也即[－V_max，V_max]和[－X_max，X_max].粒子速度和位置范围的设置原则往往依据粒子各维的变化量，由于本文粒子为ELM网络连接，故此处将粒子的速度和位置范围均设定在[－1, 1]之间.

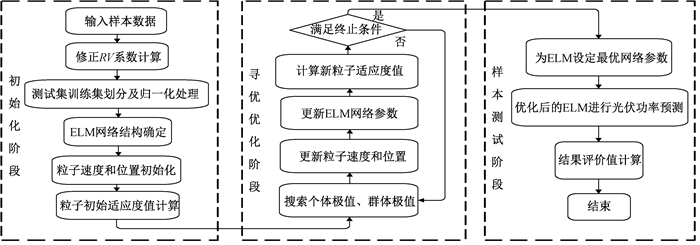
3 PSO-ELM预测模型建模流程

基于PSO与ELM组合算法的光伏发电功率预测模型的建模流程可分为初始化阶段、寻优优化阶段和样本测试阶段.根据各阶段所完成的工作，基于PSO与ELM组合算法的光伏发电功率预测模型的建模流程如图 1所示.

1) 初始化阶段.在初始化阶段里首先进行了样本数据的修正RV系数计算，根据计算结果确定网络输入数据.其次需要划分测试集和训练集.为了避免变量间不同量纲影响造成的预测误差，还需要对数据进行归一化处理，所用公式为$x = 2 \times \left( {X - {X_{\min }}} \right)/\left( {{X_{\max }} - {X_{\min }}} \right) - 1$，其中：x为归一化后的数据；X为原始数据；X_max和X_min分别对应属性数据的最大、最小值.最后由输入输出数据确定网络结构，同时初始化PSO与ELM组合模型内粒子速度和位置.根据初始化值进行粒子初始适应度值的计算，适应度函数MSE的计算公式为

$MSE = \left( {\sum\limits_{i = 1}^N {{{\left( {{{\hat X}_i} - {X_i}} \right)}^2}} } \right)/N.$

(3)

2) 寻优优化阶段.该阶段主要包括有粒子位置、速度的更新，以及新粒子适应度值的计算.其中粒子位置和速度的更新根据式(2)进行，更新过程中使每一代粒子的适应度值应朝递减的方向迭代，从而起到降低ELM预测误差的作用.而新粒子适应度值的计算，主要是用来判断更新后的粒子是否满足误差精度要求，如若满足精度要求，则直接退出寻优迭代过程.在这里除了满足精度要求外，还设置了粒子更新代数为200，当误差精度无法满足终止要求而更新代数到达设定值后，寻优迭代过程也会终止.

3) 样本测试阶段.样本测试阶段里主要是将寻优阶段保留下来的最优网络参数赋值到ELM网络中.将样本测试集中总辐射量和直射辐射量数据输入至优化后的ELM网络中，预测得到对应天气条件下的光伏发电功率，并进行相应评价值的计算.

本文仿真结果的评价值可分为计算评价值、统计评价值以及计时评价值三类.其中计算评价值反映的是预测结果与实际功率值的总体偏差情况，包含有平均绝对误差(MAE)和均方根误差(RMSE).MAE和RMSE计算公式为

$MAE = \frac{{\sum\limits_{i = 1}^N {\left| {{{\hat X}_i} - {X_i}} \right|} }}{N}, $

(4)

$RMSE = \sqrt {\frac{{\sum\limits_{i = 1}^N {\left( {{{\hat X}_i} - X_i^2} \right)} }}{N}} .$

(5)

统计评价值反映的是误差的总体分布情况，主要进行的是误差占比情况的统计.对于利用气象数据与光伏电站输出功率间统计关系进行光伏电站发电功率预测的统计方法，一般预测误差在9%~25%^[23].所以本文误差占比情况主要统计了绝对误差(E)在0~9%间和9%~25%间，以及大于25%的误差占比情况.绝对误差计算公式为

$E = \frac{{\left| {{{\hat X}_i} - {X_i}} \right|}}{{{P_N}}} \times 100\% , $

(6)

其中：式(3)~(6)中，N为预测样本数量；${\hat X_i}$为第i个样本预测值；X_i为第i个样本实际值；P_N为光伏电站的装机容量，此处P_N=100 MW.

计时评价值反映的是模型的计算效率也即算法模型的运算时长.在短期光伏发电功率预测过程中，预测结果的时效性非常重要.在保证预测精度前提下，及时地预测对应天气条件下光伏输出功率，有助于调度部门提前优化安排调度计划，所以本文将算法时长也作为一个评价指标.

4 仿真对比分析

本文选取了中国电力科学研究院采集的江苏某光伏电站2016年6月2日至2016年7月31日场站内的动态数据，共计5 760组.为了使模型得到充分的训练，此次将数据集中的前5 664组数据作为训练集，将剩余96组数据作为测试集.利用Matlab仿真软件进行了光伏发电功率值的仿真预测和相应评价值计算.

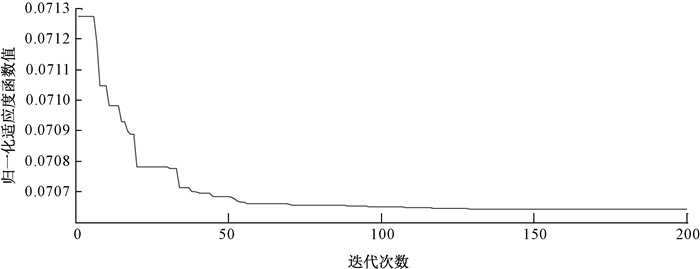
4.1 PSO-ELM仿真结果分析

1) PSO-ELM模型仿真实验时适应度值变化过程如图 2所示.由适应度函数变化图可知，在前100代的寻优迭代过程中，适应度函数值迅速下降，在100代后粒子适应度值基本保持不变.

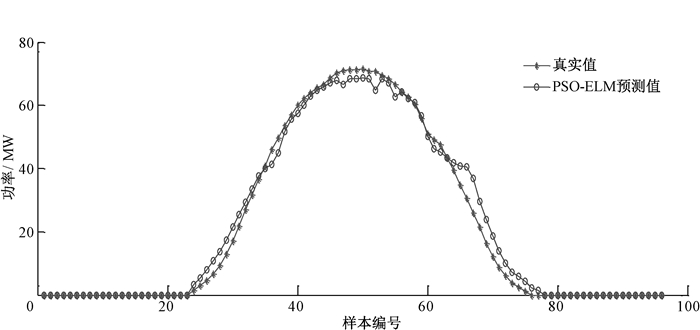
2) PSO-ELM模型预测光伏电站发电功率数据与实际光伏电站功率数据的变化波形对比如图 3所示.根据图 3可以看出，预测功率波形曲线同实际功率波形曲线基本一致.

3) PSO-ELM模型预测光伏电站发电功率误差在0~9%的占比为72%，误差在9%~25%的占比为23%，误差在25%以上的占比为5%.

4) PSO-ELM模型光伏电站发电功率预测结果的计算评价值MAE和RMSE分别为1.740 5和2.904 4，计时评价值也即算法运算时长为40.395 8 s.

4.2 仿真结果对比

本文还建立了PSO优化的BP神经网络模型，以及单一ELM模型用于光伏输出功率的仿真预测.

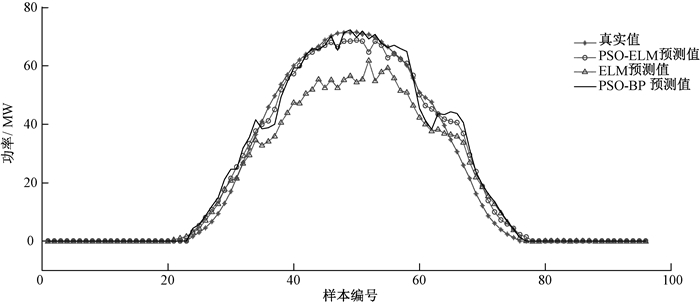
1) 各模型预测功率曲线与实际功率曲线对比如图 4所示.在功率波形曲线中，PSO-ELM和PSO-BP算法模型的功率预测结果与实际功率曲线基本相同, 但ELM单模型的功率预测曲线误差较大.

2) PSO-BP模型预测光伏电站发电功率误差在0~9%的占比为63%，误差在9%~25%的占比为13%，误差在25%以上的占比为24%.对比PSO-ELM模型预测结果可以看出，PSO-BP模型预测结果中误差低于9%的占比要低于PSO-ELM预测模型9%，误差超过25%的占比要高于PSO-ELM预测模型19%.

3) PSO-BP模型光伏电站发电功率预测结果的计算评价值MAE和RMSE分别为2.382 6和4.094 7，计时评价值也即算法运算时长为91.722 9 s.

对比两模型预测结果的评价值可知，PSO-ELM算法模型的各项指标均优于PSO-BP算法模型，其中：MAE评价指标PSO-ELM算法模型相对PSO-BP算法模型降低了26.95%；RMSE评价指标PSO-ELM算法模型相对PSO-BP算法模型降低了29.07%；在运算时长方面，PSO-ELM算法耗时较PSO-BP算法缩短了51.327 1 s，运算速率整体提高了55.96%.

5 结论

根据以上预测模型研究的对比分析，可以得出以下结论：1)采用修正RV系数的检验方法为PSO-ELM组合模型进行前期数据的组合相关性检验，很好地挖掘了数据间的内在价值、降低了数据冗余、提高了预测精度.2) PSO-ELM的组合模型能够避免传统神经网络算法中无网络参量优化的随机网络参量设置过程，提高了模型预测稳定性和准确度.3) ELM网络相对BP神经网络参数设置简单.在BP神经网络中，学习率等多个网络参量的选取较为敏感，合适的网络参量选取对预测结果影响较大，而在ELM中没有这些敏感参量的设置过程，只用设置好恰当的隐含层节点数即可.