0 引言

考虑如下部分线性固定效应面板数据模型：

$ {\mathit{\boldsymbol{Y}}_{it}} = \mathit{\boldsymbol{X}}_{it}^{\rm{T}}\mathit{\boldsymbol{\beta }} + g({U_{it}}) + {\mu _i} + {\nu _{it}}, i = 1, 2, \cdots , n, t = 1, 2, \cdots , T, $

(1)

式中：X_it为d维协变量；β为d维未知参数；g为未知光滑函数；U_it为一维协变量；ν_it是均值为0、方差为σ_v² < ∞的随机误差项，且满足E(ν_itν_{i, t-k})=0, ∀k≥2；μ_i为不可观测的个体固定效应，且与X_it和U_it存在某种未知的相关关系。模型(1)已有许多统计学者进行了研究，并广泛应用于生物医学、计量经济学、环境科学等多个领域。例如，文献[1]基于局部线性光滑和profile似然的方法研究了模型的估计问题；文献[2]提出了一种迭代非参数核估计方法，并考虑了模型结构检验等问题；文献[3]首先利用差分方法消除固定效应的影响，然后基于序列估计的方法给出模型中参数分量和非参数分量的估计；文献[4]构造了模型中参数分量的经验似然置信域；文献[5]在假定存在空间相关的情况下研究了模型中未知参数和非参数分量的估计问题。

关于面板数据序列相关检验的问题，文献[6]在T固定的情况下提出了多种检验统计量，并比较了它们的检验功效；文献[7]针对线性固定效应面板数据模型，提出了基于置换检验的方法来检验序列相关的存在性；文献[8]考虑了非参数固定效应面板数据模型的序列相关检验；文献[9]研究了半参数部分线性面板数据模型的一阶和高阶序列相关检验，但该研究并没有考虑固定效应的影响。因此，本文研究部分线性固定效应面板数据模型(1)的序列相关检验问题。不失一般性，这里仅考虑一阶序列相关性检验，即检验如下假设：

$ {\rm{H0}}:E({\nu _{it}}{\nu _{i, t - 1}}) = 0, \leftrightarrow {\rm{H}}1:E({\nu _{it}}{\nu _{i, t - 1}}) \ne 0。$

(2)

对假设检验问题(2)，本文构造了适当的检验统计量，证明其在原假设成立的条件下具有渐近正态分布，并通过数值模拟研究了检验统计量在有限样本下的表现。

1 估计方法与检验统计量构造

为消除个体效应μ_i的影响，从而保证估计量的一致性，对模型(1)进行以下差分变换：

$ {\mathit{\boldsymbol{Y}}_{it}} - {\mathit{\boldsymbol{Y}}_{i, t - 1}} = {({\mathit{\boldsymbol{X}}_{it}} - {\mathit{\boldsymbol{X}}_{i, t - 1}})^{\rm{T}}}\mathit{\boldsymbol{\beta }} + g({U_{it}}) - g({U_{i, t - 1}}) + {\nu _{it}} - {\nu _{i, t - 1}}。$

令$\Delta {\mathit{\boldsymbol{Y}}_{it}} = {\mathit{\boldsymbol{Y}}_{it}} - {\mathit{\boldsymbol{Y}}_{i, t - 1}}, \Delta {\mathit{\boldsymbol{X}}_{it}} = {\mathit{\boldsymbol{X}}_{it}} - {\mathit{\boldsymbol{X}}_{i, t - 1}}, {\varepsilon _{it}} = {\nu _{it}} - {\nu _{i, t - 1}}$，可得

$ \Delta {\mathit{\boldsymbol{Y}}_{it}} = \Delta \mathit{\boldsymbol{X}}_{it}^{\rm{T}}\mathit{\boldsymbol{\beta }} + g({U_{it}}) - g({U_{i, t - 1}}) + {\varepsilon _{it}}。$

(3)

令B(u)=(B₁(u), …, B_L(u))^T为M+1阶B样条基函数，L=K+M+1，其中K为内节点个数。于是g(u)可近似地表示为$ g(u) \approx \mathit{\boldsymbol{B}}{(u)^{\rm{T}}}\mathit{\boldsymbol{\gamma }} = \sum\limits_{l = 1}^L {{B_l}} (u){\gamma _l}, $，从而模型(3)可以表示为

$ \Delta {\mathit{\boldsymbol{Y}}_{it}} \approx \Delta \mathit{\boldsymbol{X}}_{it}^{\rm{T}}\mathit{\boldsymbol{\beta }} + \sum\limits_{l = 1}^L {{\gamma _l}} [{B_l}({U_{it}}) - {B_l}({U_{i, t - 1}})] + {\varepsilon _{it}} $

(4)

进一步，将模型(4)表示为矩阵形式

$ \Delta \mathit{\boldsymbol{Y}} \approx \Delta \mathit{\boldsymbol{X\beta }} + \mathit{\boldsymbol{D\gamma }} + \mathit{\boldsymbol{\varepsilon }}, $

(5)

式中：$\Delta \mathit{\boldsymbol{X}} = {(\Delta \mathit{\boldsymbol{X}}_1^{\rm{T}}, \cdots , \Delta \mathit{\boldsymbol{X}}_n^{\rm{T}})^{\rm{T}}}, \Delta {\mathit{\boldsymbol{X}}_i} = {(\Delta {\mathit{\boldsymbol{X}}_{i1}}, \cdots , \Delta {\mathit{\boldsymbol{X}}_{iT}})^{\rm{T}}}$；ΔY的定义与ΔX类似；$\mathit{\boldsymbol{\varepsilon }} = {(\mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}, \mathit{\boldsymbol{\varepsilon }}_2^{\rm{T}}, \cdots , \mathit{\boldsymbol{\varepsilon }}_n^{\rm{T}})^{\rm{T}}}, {\mathit{\boldsymbol{\varepsilon }}_i} = {({\mathit{\boldsymbol{\varepsilon }}_{i1}}, {\mathit{\boldsymbol{\varepsilon }}_{i2}}, \cdots , {\mathit{\boldsymbol{\varepsilon }}_{iT}})^{\rm{T}}};\mathit{\boldsymbol{\gamma }} = {({\gamma _1}, {\gamma _2}, \cdots , {\gamma _L})^{\rm{T}}}$；$ \mathit{\boldsymbol{D}} = {({\mathit{\boldsymbol{D}}_1}, {\mathit{\boldsymbol{D}}_2}, \cdots , {\mathit{\boldsymbol{D}}_n})^{\rm{T}}}, {\mathit{\boldsymbol{D}}_i} = {({\mathit{\boldsymbol{W}}^{\rm{T}}}({U_{i1}}), {\mathit{\boldsymbol{W}}^{\rm{T}}}({U_{i2}}), \cdots , {\mathit{\boldsymbol{W}}^{\rm{T}}}({U_{iT}}))^{\rm{T}}} $,$ \mathit{\boldsymbol{W}}({U_{it}}) = {({B_1}({U_{it}}) - {B_1}({U_{i, t - 1}}), {B_2}({U_{it}}) - {B_2}({U_{i, t - 1}}), \cdots , {B_L}({U_{it}}) - {B_L}({U_{i, t - 1}}))^{\rm{T}}}$。进一步，令${\mathit{\boldsymbol{M}}_D} = {\mathit{\boldsymbol{I}}_{n(T - 1)}} - \mathit{\boldsymbol{D}}{({\mathit{\boldsymbol{D}}^{\rm{T}}}\mathit{\boldsymbol{D}})^{ - 1}}{\mathit{\boldsymbol{D}}^{\rm{T}}}$，其中I_n(T-1)是n×(T-1)维单位阵，显然有M_DDγ=0。

(5) 式两端同时乘以M_D，有${\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{Y}} \approx {\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X\beta }} + {\mathit{\boldsymbol{M}}_D}\mathit{\boldsymbol{\varepsilon }}$。因此，由最小二乘估计方法可得参数分量β的估计为$\mathit{\boldsymbol{\hat \beta }} = {(\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X}})^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{Y}}$。将$\mathit{\boldsymbol{\hat \beta }}$带入(5)式可得样条系数γ的估计为$ \mathit{\boldsymbol{\hat \gamma }} = {({\mathit{\boldsymbol{D}}^{\rm{T}}}\mathit{\boldsymbol{D}})^{ - 1}}{\mathit{\boldsymbol{D}}^{\rm{T}}}(\Delta \mathit{\boldsymbol{Y}} - \Delta \mathit{\boldsymbol{X\hat \beta }})$，从而非参数函数$\hat g(u) = \mathit{\boldsymbol{B}}{(u)^{\rm{T}}}\mathit{\boldsymbol{\hat \gamma }}$。

对模型(1)采用一阶差分变换后，随机误差项转化为ε_it=ν_it-ν_{i, t-1}。由于误差序列ν_it不存在高阶相关，从而检验原假设H0:E(ν_itν_{i, t-1})=0等价于检验H0:E(ε_itε_{i, t-2})=0。因为

$ E({\varepsilon _{it}}{\varepsilon _{i, t - 2}}) = E({\nu _{it}}{\nu _{i, t - 2}} - {\nu _{it}}{\nu _{i, t - 3}} - {\nu _{i, t - 1}}{\nu _{i, t - 2}} + {\nu _{i, t - 1}}{\nu _{i, t - 3}}) = - E({\nu _{i, t - 1}}{\nu _{i, t - 2}}) = - E({\nu _{it}}{\nu _{i, t - 1}})。$

于是，对于假设检验问题(2)，基于E(ε_itε_{i, t-2})构造如下检验统计量：

$ {I_n} = \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{t = 4}^T {{{\hat \varepsilon }_{it}}} } {\hat \varepsilon _{i, t - 2}}, $

式中：${T_3} = T - 3, {\hat \varepsilon _{it}} = {\mathit{\boldsymbol{Y}}_{it}} - {\mathit{\boldsymbol{Y}}_{i, t - 1}} - {({\mathit{\boldsymbol{X}}_{it}} - {\mathit{\boldsymbol{X}}_{i, t - 1}})^{\rm{T}}}\mathit{\boldsymbol{\hat \beta }} - (\hat g({U_{it}}) - \hat g({U_{i, t - 1}}))$。

2 渐近结果

为了得到I_n的渐近分布，需要以下条件。

C1：对于固定t，U_it有以[a，b]为支撑的分布，且存在Lipschitz密度函数p_t(·)，使得$0 < \mathop {{\rm{inf}}}\limits_{a \le u \le b} {p_t}(u) \le \mathop {{\rm{sup}}}\limits_{a \le u \le b} {p_t}(u) < \infty $。

C2：g(u)在[a，b]上有有界的r(r≥2)阶连续导数。

C3：令c₁, c₂, …, c_K为区间[a，b]上的内节点，并令${c_0} = a, {c_{K + 1}} = b, {h_i} = {c_i} - {c_{i - 1}}, h = {\rm{max}}\left\{ {{h_i}} \right\}$，那么存在常数C使得$h/{\rm{min}}\{ {h_i}\} < C, {\rm{max}}\{ {h_{i + 1}} - {h_i}\} = o({K^{ - 1}})$。

C4：存在正常数c₁和c₂，使得${c_1}{I_d} \le E({\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i.}}\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i.}^{\rm{T}}) \le {c_2}{I_d}$，其中$ {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i.}} = ({\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i1}}, \cdots , {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{iT}}), {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{it}} = {\mathit{\boldsymbol{X}}_{it}} - {\mathit{\boldsymbol{H}}_t}({U_{it}})$，${\mathit{\boldsymbol{H}}_t}({U_{it}}) = {({h_{t1}}({U_{it}}), \cdots , {h_{td}}({U_{it}}))^{\rm{T}}}, {h_{tj}}(u) = E({X_{it, j}}|{U_{it}} = u)$。

C5：随机变量$({\mathit{\boldsymbol{Y}}_i}, {\mathit{\boldsymbol{X}}_i}, {U_i}, {\mu _i}, {v_i})$独立同分布，$({\mathit{\boldsymbol{Y}}_{it}}, {\mathit{\boldsymbol{X}}_{it}}, {U_{it}}, {\nu _{it}})$关于t严平稳。

C6：在H0成立的条件下，$E({\nu _{it}}|{\mathit{\boldsymbol{X}}_{it}}, {\mathit{\boldsymbol{X}}_{i, t - 1}}, \cdots , {\mathit{\boldsymbol{X}}_{i1}}, {U_{it}}, {\mu _i}) = 0$。

C7：T固定，n→∞且内节点个数$K = {O_p}({n^{1/(2r + 1)}})$。

条件C1和C2是非参数估计中的常见假设，C3和C7是B样条估计的基本假设，C4和C5是研究半参数面板数据模型估计的常用假设，C6是对误差项期望的常规设定。

定理1  假定条件C1~C7成立，则有

$ \sqrt {nT} (\mathit{\boldsymbol{\hat \beta }} - \mathit{\boldsymbol{\beta }}){ \to _L}N(0, \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1^{ - 1}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1^{ - 1}), $

式中：${\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1} = {T^{ - 1}}E\{ \Delta {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i.}}\Delta \mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i.}^{\rm{T}}\} , \Delta {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i.}} = (\Delta {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i1}}, \cdots , \Delta {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{iT}});{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2} = {T^{ - 1}}E\{ \Delta {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i.}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} \boldsymbol{\varDelta} \boldsymbol{\varPi} }}_{i.}^{\rm{T}}\} , \mathit{\boldsymbol{ \boldsymbol{\varSigma} }} = E({\mathit{\boldsymbol{\varepsilon }}_i}\mathit{\boldsymbol{\varepsilon }}_i^{\rm{T}})$。$\Delta {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{it}} = ({\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i2}} - {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i1}}, \cdots , {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{it}} - {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{i, t - 1}}), \Delta {\mathit{\boldsymbol{H}}_t}({U_{it}}) = {(\Delta {h_{t1}}({U_{it}}), \cdots , \Delta {h_{td}}({U_{it}}))^{\rm{T}}}$，$\Delta {h_{tj}}({U_{it}}) = {h_{tj}}({U_{it}}) - {h_{t - 1, j}}({U_{i, t - 1}}), j = 1, 2, \cdots , d$。

定理2  假定条件C1~C7成立，则有$ \left\| {\hat g(u) - g(u)} \right\|_2^2 = {O_p}({n^{ - 2r/(2r + 1)}})$。

定理3  假定条件C1~C7成立，且当原假设H0:E(ε_itε_{i, t-2})=0成立时，有

$ {J_n} = \sqrt {n{T_3}} {I_n}/\hat \sigma _\varepsilon ^2{ \to _L}N(0, 1), $

式中：$\hat \sigma _\varepsilon ^2$是$\sigma _\varepsilon ^2 = E(\varepsilon _{it}^2|{\mathit{\boldsymbol{X}}_{it}}, {U_{it}})$的相合估计，$\hat \sigma _\varepsilon ^2 = \frac{1}{{n{T_2}}}\sum\limits_{i = 1}^n {\sum\limits_{t = 3}^T {\hat \varepsilon _{it}^2} } , {T_2} = T - 2$。

当${\rm{H}}1:E({\varepsilon _{it}}{\varepsilon _{i, t - 2}}) \ne 0$成立时，ν_it是序列相关的，从而有${I_n}{ \to _P}E({\varepsilon _{it}}{\varepsilon _{i, t - 2}}) \ne 0$。又因为$\hat \sigma _\varepsilon ^2 = {O_P}(1)$，所以J_n以n的速度趋于无穷大。因此，当n→∞时, 构造的检验统计量以趋近于1的概率拒绝原假设H0。

3 数值模拟

通过数值模拟来验证本文所提出的估计以及一阶序列相关检验方法的有效性。

例1(误差服从对称分布)  考虑从如下模型产生数据：

$ {Y_{it}} = {X_{it, 1}}{\beta _1} + {X_{it, 2}}{\beta _2} + g({U_{it}}) + {\mu _i} + {\nu _{it}}, i = 1, 2, \cdots , n, t = 1, 2, \cdots , T, $

式中：${X_{it, 1}}\backsim N(1, 2.25);{X_{it, 2}}\backsim N(0, 1);{U_{it}}\backsim U(0, 1), g({U_{it}}) = {\rm{sin}}(\pi {U_{it}});{\beta _1} = 2;{\beta _2} = 3$。

固定效应的产生方式为

$ {\mu _i} = {\bar X_{i, 1}} + {\omega _i}, $

其中:${\bar X_{i, 1}} = \frac{1}{T}\sum\limits_{i = 1}^T {{X_{it, 1}}} ;{\omega _i}\backsim N(0, 1)$。

在数值模拟中使用立方B样条基函数，内节点个数K采用交叉验证方法选取，样本容量n分别为50、100和150，T分别为5和8，重复模拟计算1 000次。首先验证估计方法的有效性。考虑如下误差结构：ν_it=δe_{i, t-1}+e_it，其中e_it~N(0, 1)，δ分别取0和0.4。

δ=0时对应于误差序列不相关的假设，δ=0.4时对应于误差序列相关的假设，参数估计的有限样本表现如表 1所示。可以看出，随着样本量的增加，参数估计的均值越来越接近于真值，且它们的标准差(SD)和均方误差(MSE)均减小；不存在误差序列相关时参数估计的Bias、SD和MSE明显要比存在序列相关时小，这也进一步表明了模型估计之前检验序列相关的必要性。

下面研究一阶序列相关检验统计量的检验功效。考虑如下2种情形：

(i) ν_it~N(0, 1)或t(2)；

(ii) ν_it=δe_{i, t-1}+e_it，其中e_it~N(0, 1)或t(2)。

情形(i)对应于误差序列不相关的假设，取正态误差和非正态误差两种误差结构。对于情形(i)，检验统计量在显著性水平α=0.05下的经验拒绝频率模拟结果见表 2。情形(ii)对应于误差序列相关的假设，取δ=0, 0.1, 0.2, …, 1.1。当δ=0时，误差不存在相关性，转化为情形(i)。

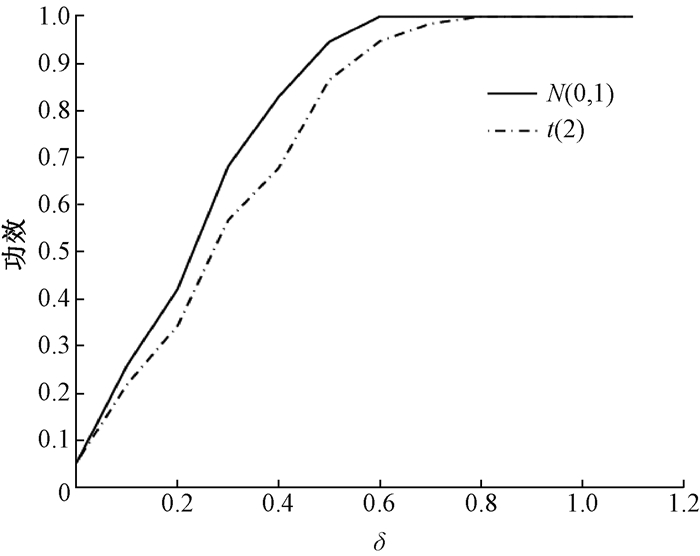
图 1给出了n=100，T=8时的检验功效函数。从图 1可以看出，当原假设成立，即δ=0时，检验统计量的功效接近0.05；当备择假设成立，即δ > 0时，检验统计量的功效随着δ的增加而快速变大。结果表明，所构造的检验统计量对备择假设是敏感的。从表 2也可以看出，经验拒绝频率都接近理论水平0.05，且所提方法对误差分布假设也是稳健的。因此，本文提出的序列相关检验方法是可行的。

例2(误差服从非对称分布)   从模型(1)产生数据，其中X_it服从均值为1、协方差阵为I₁₀的p=10维正态分布，β=(2, 2, …, 2)^T，U_it、μ_i和g(u)的设置方式与例1相同。考虑如下非对称分布误差结构：ν_it=δe_{i, t-1}+e_it，其中e_it~0.3χ²(3)+0.7 N(-1, 1)，δ分别取0和0.6。

δ=0时对应于误差序列不相关的假设，即原假设；δ=0.6时对应于误差序列相关的假设，即备择假设。非对称误差分布情形下检验统计量在显著性水平α=0.05和α=0.1下的经验拒绝频率模拟结果见表 3。可以看出，在非对称误差分布情形下，检验统计量仍表现良好。当模型中不存在误差序列相关时，经验拒绝频率均接近显著性水平，且随着n和T的增大表现趋好。当模型中存在误差序列相关时，检验功效随着n和T的增大越来越趋近于1。

4 定理证明

引理1  若g(u)满足条件C2，则存在常数C使得$\mathop {{\rm{sup}}}\limits_{u \in [a, b]} |g(u) - {\mathit{\boldsymbol{B}}^{\rm{T}}}(u)\mathit{\boldsymbol{\gamma }}| \le CK_{}^{ - r}$。

证明  引理1的证明类似于文献[10]中推论6.21的证明，此处省略。

定理1的证明  简单计算可得

$ \begin{array}{l} \mathit{\boldsymbol{\hat \beta }} - \mathit{\boldsymbol{\beta }} = {(\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X}})^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{\beta }} = {(\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X}})^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}(\Delta \mathit{\boldsymbol{X\beta }} + \Delta g + \mathit{\boldsymbol{\varepsilon }}) - \mathit{\boldsymbol{\beta }} = \\ \Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X}}{)^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X\beta }} + {(\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X}})^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta g + {(\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X}})^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\mathit{\boldsymbol{\varepsilon }} - \mathit{\boldsymbol{\beta }} = \\ {(\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X}})^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta g + {(\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X}})^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\mathit{\boldsymbol{\varepsilon }}, \end{array} $

其中$\Delta g = g({U_{it}}) - g({U_{i, t - 1}})$。

类似于文献[9]中引理A.2的证明，易证${n^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\mathit{\boldsymbol{\varepsilon }} = {n^{ - 1}}\Delta \mathit{\boldsymbol{ \boldsymbol{\varPi} \varepsilon }} + {o_p}({n^{ - 1/2}}), {n^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}g = {o_p}({n^{ - 1/2}})$，以及$ {n^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X}} = {n^{ - 1}}\Delta {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}^{\rm{T}}}\Delta \mathit{\boldsymbol{ \boldsymbol{\varPi} }} + {o_p}(1)$。于是有

$ \begin{array}{*{20}{l}} {\sqrt {nT} (\mathit{\boldsymbol{\hat \beta }} - \mathit{\boldsymbol{\beta }}) = \sqrt {nT} {{(\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X}})}^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D} + \sqrt {nT} {{(\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}\Delta \mathit{\boldsymbol{X}})}^{ - 1}}\Delta {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_D}g = }\\ {\sqrt {nT} {{(\Delta {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}^{\rm{T}}}\Delta \mathit{\boldsymbol{ \boldsymbol{\varPi} }})}^{ - 1}}\Delta {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}^{\rm{T}}}\mathit{\boldsymbol{\varepsilon }} + {o_p}(1)}。\end{array} $

因此，由Lindeberg中心极限定理，易得$\sqrt {nT} (\mathit{\boldsymbol{\hat \beta }} - \mathit{\boldsymbol{\beta }}){ \to _L}N(0, \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1^{ - 1}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_2}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1^{ - 1})$。

定理2的证明  由引理1和定理1，类似于文献[11]中定理2的证明，可证定理2成立。

定理3的证明  简单计算可得${\hat \varepsilon _{it}} = {\varepsilon _{it}} - {\hat \zeta _{it}} - {\hat \eta _{it}}$, 其中${\hat \eta _{it}} = ({\hat g_{it}} - {g_{it}}) - ({\hat g_{i, t - 1}} - {g_{i, t - 1}}), {\hat \zeta _{it}} = \Delta \mathit{\boldsymbol{X}}_{it}^{\rm{T}}(\mathit{\boldsymbol{\hat \beta }} - \mathit{\boldsymbol{\beta }})$。从而有

$ {\hat \varepsilon _{it}}{\hat \varepsilon _{i, t - 2}} = {\varepsilon _{it}}{\varepsilon _{i, t - 2}} - {\varepsilon _{it}}{\hat \zeta _{i, t - 2}} - {\varepsilon _{it}}{\hat \eta _{i, t - 2}} - {\hat \zeta _{it}}{\varepsilon _{i, t - 2}} - {\hat \zeta _{it}}{\hat \zeta _{i, t - 2}} - {\hat \zeta _{it}}{\hat \eta _{i, t - 2}} - {\hat \eta _{it}}{\varepsilon _{i, t - 2}} - {\hat \eta _{it}}{\hat \zeta _{i, t - 2}} + {\hat \eta _{it}}{\hat \eta _{i, t - 2}}。$

可得I_n的新展式为

$ \begin{array}{l} {I_n} = \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{{\hat \varepsilon }_{it}}} } {{\hat \varepsilon }_{i, t - 2}} = \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{t = 4}^T {{\varepsilon _{it}}} } {\varepsilon _{i, t - 2}} - \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{\varepsilon _{it}}} } {{\hat \zeta }_{i, t - 2}} - \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{t = 4}^T {{\varepsilon _{it}}} } {{\hat \eta }_{i, t}} - \\ \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{{\hat \zeta }_{it}}} } {\varepsilon _{i, t - 2}} - \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{{\hat \zeta }_{it}}} } {{\hat \zeta }_{i, t - 2}} - \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{{\hat \zeta }_{it}}} } {{\hat \eta }_{i, t - 2}} - \\ \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{{\hat \eta }_{it}}} } {\varepsilon _{i, t - 2}} - \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{{\hat \eta }_{it}}} } {{\hat \zeta }_{i, t - 2}} + \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{t = 4}^T {{{\hat \eta }_{it}}} } {{\hat \eta }_{i, t - 2}} = \\ {A_{1n}} - {A_{2n}} - {A_{3n}} - {A_{4n}} - {A_{5n}} - {A_{6n}} - {A_{7n}} - {A_{8n}} + {A_{9n}}。\end{array} $

由定理1和定理2，简单计算可得${A_{2n}} = {o_p}({n^{ - 1/2}}), {A_{4n}} = {o_p}({n^{ - 1/2}}), {A_{5n}} = {o_p}({n^{ - 1/2}}), {A_{6n}} = {o_p}({n^{ - 1/2}}), {A_{8n}} = {O_p}({n^{ - 1/2}})$。下面考虑A_3n，可得

$ {A_{3n}} = \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{\varepsilon _{it}}} } ({\hat g_{i, t - 2}} - {g_{i, t - 2}}) - \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{\varepsilon _{it}}} } ({\hat g_{i, t - 3}} - {g_{i, t - 3}}) = {A_{3n.1}} + {A_{3n.2}}。$

简单计算可知

$ {A_{3n.1}} = \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{t = 4}^T {{\nu _{it}}} } ({\hat g_{i, t - 2}} - {g_{i, t - 2}}) - \frac{1}{{n{T_3}}}\sum\limits_{i = 1}^n {\sum\limits_{t = 4}^T {{\nu _{i, t - 1}}} } ({\hat g_{i, t - 2}} - {g_{i, t - 2}})。$

又因

$ \sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{\nu _{it}}} } ({\hat g_{i, t - 2}} - {g_{i, t - 2}}) = \sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{\nu _{it}}} } (\hat g({u_{i, t - 2}}) - g({u_{i, t - 2}})) = {\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{\nu , }} $

式中：$\mathit{\boldsymbol{G}} = {[\hat g({u_{1, 2}}) - g({u_{1, 2}}), \cdots , \hat g({u_{n, T - 2}}) - g({u_{n, T - 2}})]^{\rm{T}}};\mathit{\boldsymbol{\nu }} = {({\nu _{11}}, \cdots , {\nu _{nT}})^{\rm{T}}}$。

进一步可得

$ Var ({\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{\nu }}) = {\mathit{\boldsymbol{G}}^{\rm{T}}} Var (\mathit{\boldsymbol{\nu }})\mathit{\boldsymbol{G}} \le C{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}} = C\sum\limits_{i = 1}^n {\sum\limits_{i = 4}^T {{{({{\hat g}_{i, t - 2}} - {g_{i, t - 2}})}^2}} } , $

所以有A_3n.1=o_p(n^-1/2)。同理，可以证得A_3n.2=o_p(n^-1/2)，故A_3n=o_p(n^-1/2)。类似地，由定理2易证${A_{7n}} = {o_p}({n^{ - 1/2}}), {A_{9n}} = {o_p}({n^{ - 1/2}})$。

综上所述，在原假设成立的条件下，有$\sqrt {n{T_3}} {I_n} = \sqrt {n{T_3}} {A_{1n}} + {o_p}(1){ \to _L}N(0, \sigma _\varepsilon ^4)$，进而$\sqrt {n{T_3}} {I_n}/\sigma _\varepsilon ^2{ \to _L}N(0, 1)$。此外，又因$\hat \sigma _\varepsilon ^2 = \frac{1}{{n{T_2}}}\sum\limits_{i = 1}^n {\sum\limits_{t = 3}^T {\varepsilon _{it}^2} } + {o_p}(1){ \to _P}\sigma _\varepsilon ^2$，故$\sqrt {n{T_3}} {I_n}/\hat \sigma _\varepsilon ^2{ \to _L}N(0, 1)$。定理3证明完毕。