用随机微分方程来描述客观现象在实际应用中有着越来越重要的作用[1-6], 通常用数值方法得到的解来近似方程的解析解.人们主要研究数值求解方法的收敛性[7]和稳定性, 研究的较多的是Euler方法、Milstein方法及Runge-Kutta方法.近年来又提出Heun方法, 本文在该数值方法的基础上构造出θ-Heun方法, 并研究了该方法用于求解标量自治随机微分方程的收敛性.
1 随机微分方程及数值求解方法 1.1 随机微分方程及性质一维标量自治的随机微分方程[8]:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{d}}X\left( t \right) = f\left( {X\left( t \right)} \right){\rm{d}}t + g\left( {X\left( t \right)} \right){\rm{d}}w\left( t \right), }&{t \in [{t_0}, T], }\\ {X({t_0}) = {X_0}, }&{X \in {\bf{R}}, } \end{array}} \right. $ | (1) |
其中:f(X), g(X)在[t0, T]上连续可测; E|X0|2 < ∞; w(t)是标准的winner过程, 且与X0相互独立.当t>0, 步长h>0时, 增量Δw(t)=w(t+h)-w(t)是一列服从正态分布N(0, h), 且相互独立的随机变量, 有如下性质[9].
1) E[∫abg(X(t))dw(t)]=0, a < b.
2) E[|∫abg(X(t))dw(t)|2]=∫cdE[|g(X(t))|2]dt, c < d.
1.2 θ-Heun方法定义1 求解随机微分方程(1)的θ-Heun方法为
| $ \begin{array}{l} {X_{n + 1}} = {X_n} + h[\left( {1 - \theta } \right)f({X_n}) + \theta f({X_n} + hf({X_n}))] + \\ g({X_n})\Delta {w_n}, \theta \in \left[ {0, 1} \right]. \end{array} $ | (2) |
定义2[8] 记X(tn)为随机微分方程(1)在网格点tn处的精确值, Xn为通过方法(2)得到的随机微分方程(1)的数值解,
| $ \begin{array}{l} {\delta _{n + 1}} = X({t_{n + 1}}) - \tilde X({t_{n + 1}}), \;\;{\varepsilon _{n + 1}} = \\ X({t_{n + 1}}) - {X_{n + 1}}, \;n = 0, 1, \cdots , N - 1. \end{array} $ |
定义3[6] 如果存在常数C>0(C与h无关), 则
引理1(Hölder不等式)[6] 如果函数f(x)与g(x)在区间[a, b]上连续可积, 则
| $ \smallint _a^bf\left( x \right)g\left( x \right){\rm{d}}x \le {(\smallint _a^b{\left( {f\left( x \right)} \right)^p}{\rm{d}}x)^{\frac{1}{p}}}{(\smallint _a^b{\left( {g\left( x \right)} \right)^q}{\rm{d}}x)^{\frac{1}{q}}}. $ |
引理2[6] 如果f(X)、g(X)满足以下条件:
1) 线性增长条件.存在一个正的常数L1, 使
|f(X)|∨|g(X)|≤L1(1+|X|), 或|f(X)|2∨|g(X)|2≤L1(1+|X|2).
2) Lipschitz条件.存在一个正的常数L2, 使|f(X)-f(Y)|∨|g(X)-g(Y)|≤L2|X-Y|, ∀X, Y∈R. “∨”表示两函数中较大者, 若f(X), g(X)满足条件1)和2), 则方程(1)的解满足
ⅰ)
ⅱ) ∀t0≤s≤t≤T, E|X(t)-X(s)|2≤C2(t-s).
其中:C1、C2为仅依赖于初值X0和T的常数.
引理3[10] 对于方程(1), 当h→0且ε0=0时, 若
定理1 若f(X)、g(X)满足引理1和2, 对于θ-Heun方法, p1=2, p2=1, p=1(步长h≤1).
下面证明p1=2.
证明
| $ \begin{array}{l} {\delta _{n + 1}} = X({t_{n + 1}}) - \tilde X({t_{n + 1}}) = \\ [X({t_n}) + \smallint _{{t_n}}^{{t_{n + 1}}}f\left( {X\left( s \right)} \right){\rm{d}}s + \smallint _{{t_n}}^{{t_{n + 1}}}g\left( {X\left( s \right)} \right){\rm{d}}w] - \\ [X({t_n}) + h[\left( {1 - \theta } \right)f(X({t_n})) + \theta f(X({t_n}) + hf(X({t_n})))] + \\ g(X({t_n}))\Delta {w_n}] = \smallint _{{t_n}}^{{t_{n + 1}}}[f\left( {X\left( s \right)} \right) - f(X({t_n}))]{\rm{d}}s + \\ \smallint _{{t_n}}^{{t_{n + 1}}}[g\left( {X\left( s \right)} \right) - g(X({t_n}))]{\rm{d}}w - h\theta (f(X({t_n}) + hf(X({t_n}))) - f(X({t_n}))). \end{array} $ | (3) |
对上式两端同时取期望有
| $ \begin{array}{l} E({\delta _{n + 1}}) \le E\smallint _{{t_n}}^{{t_{n + 1}}}[f\left( {X\left( s \right)} \right) - f(X({t_n}))]{\rm{d}}s + E\smallint _{{t_n}}^{{t_{n + 1}}}\\ [g\left( {X\left( s \right)} \right) - g(X({t_n}))]{\rm{d}}w + h\theta E\\ (f(X({t_n}) + hf(X({t_n}))) - f(X({t_n}))). \end{array} $ |
根据w(t)的性质1)可知
| $ \begin{array}{l} E\smallint _{{t_n}}^{{t_{n + 1}}}[g\left( {X\left( s \right)} \right) - g(X({t_n}))]{\rm{d}}w\left( s \right) = 0, \\ E({\delta _{n + 1}}) \le E\smallint _{{t_n}}^{{t_{n + 1}}}[f\left( {X\left( s \right)} \right) - f(X({t_n}))]{\rm{d}}s + \\ hE(f(X({t_n}) + hf(X({t_n}))) - f(X({t_n}))), \\ |E({\delta _{n + 1}})| \le |E\smallint _{{t_n}}^{{t_{n + 1}}}[f\left( {X\left( s \right)} \right) - f(X({t_n}))]{\rm{d}}s| + \\ h|E(f(X({t_n}) + hf(X({t_n}))) - f(X({t_n})))|. \end{array} $ |
A)根据引理2的(2)和(3)式及w(t)的性质1)有
| $ \begin{array}{l} |E\smallint _{{t_n}}^{{t_{n + 1}}}[f\left( {X\left( s \right)} \right) - f(X({t_n}))]{\rm{d}}s| \le {L_2}E\smallint _{{t_n}}^{{t_{n + 1}}}\\ |X\left( s \right) - X({t_n})|{\rm{d}}s = {L_2}E\smallint _{{t_n}}^{{t_{n + 1}}}|X({t_n}) + \smallint _{{t_n}}^s\\ f\left( {X\left( u \right)} \right){\rm{d}}u + \smallint _{{t_n}}^sg\left( {X\left( u \right)} \right){\rm{d}}w\left( u \right) - X({t_n})\\ |{\rm{d}}s \le {L_2}E\smallint _{{t_n}}^{{t_{n + 1}}}\smallint _{{t_n}}^s|f\left( {X\left( u \right)} \right)|{\rm{d}}u{\rm{d}}s + {L_2}E\smallint _{{t_n}}^{{t_{n + 1}}}\smallint _{{t_n}}^s\\ |g\left( {X\left( u \right)} \right)|{\rm{d}}w\left( u \right){\rm{d}}s \le {L_1}{L_2}E\smallint _{{t_n}}^{{t_{n + 1}}}\smallint _{{t_n}}^s\left( {1 + |X\left( u \right)|} \right)\\ {\rm{d}}u{\rm{d}}s \le {L_1}{L_2}E\smallint _{{t_n}}^{{t_{n + 1}}}\smallint _{{t_n}}^s(1 + \frac{1}{2}({1^2} + {\left| {X\left( u \right)} \right|^2})){\rm{d}}u{\rm{d}}s \le \\ {L_1}{L_2}\smallint _{{t_n}}^{{t_{n + 1}}}\smallint _{{t_n}}^s(3 + E{\left| {X\left( u \right)} \right|^2}){\rm{d}}u{\rm{d}}s \le {L_1}{L_2}\smallint _{{t_n}}^{{t_{n + 1}}}\smallint _{{t_n}}^s(3 + {C_1}){\rm{d}}u{\rm{d}}s \le {L_1}{L_2}(3 + {C_1}){h^2}. \end{array} $ |
B) 根据引理2有
| $ \begin{array}{l} h|E(f(X({t_n}) + hf(X({t_n}))) - f(X({t_n})))| \le {L_2}hE|\\ X({t_n}) + hf(X({t_n})) - X({t_n})| \le {L_1}{L_2}{h^2}E(1 + |X({t_n})|)\\ \le {L_1}{L_2}{h^2}E(1 + \frac{1}{2}({1^2} + |X({t_n}){|^2})) \le {L_1}{L_2}{h^2}\\ (3 + E|X({t_n}){|^2}) \le {L_1}{L_2}(3 + {C_1}){h^2}, \end{array} $ |
从而|E(δn+1)|≤2L1L2(3+C1)h2, 记C3=2L1L2(3+C1), 则
下面证明p2=1.
证明 由(3)式及(a+b+c)2≤3a2+3b2+3c2得
| $ \begin{array}{l} |{\delta _{n + 1}}{|^2} \le 3|\smallint _{{t_n}}^{{t_{n + 1}}}[f\left( {X\left( s \right)} \right) - f(X({t_n}))]{\rm{d}}s{|^2} + 3|\smallint _{{t_n}}^{{t_{n + 1}}}\\ [g\left( {X\left( s \right)} \right) - g(X({t_n}))]{\rm{d}}w\left( s \right){|^2} + 3{h^2}{\theta ^2}|f(X({t_n}) + \\ hf(X({t_n}))) - f(X({t_n})){|^2}, E|{\delta _{n + 1}}{|^2} \le 3E|\smallint _{{t_n}}^{{t_{n + 1}}}\\ [f\left( {X\left( s \right)} \right) - f(X({t_n}))]{\rm{d}}s{|^2} + 3E|\smallint _{{t_n}}^{{t_{n + 1}}}[g\left( {X\left( s \right)} \right) - \\ g(X({t_n}))]{\rm{d}}w\left( s \right){|^2} + 3{h^2}E|f(X({t_n}) + hf(X({t_n}))) - f(X({t_n})){|^2}.\\ {\rm{A}})\;E|\smallint _{{t_n}}^{{t_{n + 1}}}[f\left( {X\left( s \right)} \right) - f(X({t_n}))]{\rm{d}}s{|^2} \le E{(\smallint _{{t_n}}^{{t_{n + 1}}}|f\left( {X\left( s \right)} \right) - f(X({t_n}))|{\rm{d}}s)^2}. \end{array} $ | (4) |
由Hölder不等式得
| $ \begin{array}{l} h\smallint _{{t_n}}^{{t_{n + 1}}}E|f\left( {X\left( s \right)} \right) - f(X({t_n})){|^2}{\rm{d}}s \le {L_2}^2h\smallint _{{t_n}}^{{t_{n + 1}}}\\ E|X\left( s \right) - X({t_n}){|^2}{\rm{d}}s \le {L_2}^2{C_2}h\smallint _{{t_n}}^{{t_{n + 1}}}(s - {t_n}){\rm{d}}s \le {L_2}^2{C_2}{h^3}. \end{array} $ |
B) 根据w(t)的性质2)及引理2有
| $ \begin{array}{l} E|\smallint _{{t_n}}^{{t_{n + 1}}}[g\left( {X\left( s \right)} \right) - g(X({t_n}))]{\rm{d}}w\left( s \right){|^2} = \smallint _{{t_n}}^{{t_{n + 1}}}\\ E|g\left( {X\left( s \right)} \right) - g(X({t_n})){|^2}{\rm{d}}s \le {L_2}^2\smallint _{{t_n}}^{{t_{n + 1}}}E\\ |X\left( s \right) - X({t_n}){|^2}{\rm{d}}s \le {L_2}^2{C_2}\smallint _{{t_n}}^{{t_{n + 1}}}(s - {t_n}){\rm{d}}s = {L_2}^2{C_2}{h^2}. \end{array} $ |
C) 由引理2可得
| $ \begin{array}{l} E|f[X({t_n}) + hf(X({t_n}))] - f(X({t_n})){|^2} \le {L_2}^2E\\ |X({t_n}) + hf(X({t_n})) - X({t_n}){|^2} = {L_2}^2{h^2}E|f(X({t_n})){|^2}\\ \le {L_2}^2{L_1}{h^2}E(1 + |X({t_n}){|^2}) = {L_2}^2{L_1}{h^2}(1 + E(|X({t_n}){|^2}))\\ \le {L_2}^2{L_1}{h^2}(1 + {C_1}). \end{array} $ |
由A)、B)、C)得
| $ \begin{array}{l} E|{\delta _{n + 1}}{|^2} \le 3{L_2}^2{C_2}{h^3} + 3{L_2}^2{C_2}{h^2} + 3{L_2}^2\\ {L_1}{h^4}(1 + {C_1}) \le 3{L_2}^2(2{C_2} + {L_1}(1 + {C_1})){h^2}.{\rm{ }} \end{array} $ |
记C4=3L22(C2+L1(1+C1)), 则E|δn+1|2≤C4h2, 从而
下面证明p=1.
证明 根据定义1得εn+1=X(tn+1)-Xn+1=[X(tn+1)-
A) 由引理2的2)及εn的定义得h(1-θ)E|f(X(tn))-f(Xn)|≤L2hE|X(tn)-Xn|=L2hE|εn|.
B) 由引理2的2)及w(t)与Xn的独立性[8]得
| $ E|(g(X({t_n})) - g({X_n}))\Delta {w_n}| \le {L_2}E|(X({t_n}) - {X_n})\Delta {w_n}| = {L_2}E|{\varepsilon _n}\left| E \right|\Delta {w_n}|. $ |
因为Δw(t)~N(0, h), 根据正态分布的定义得
| $ E|(g(X({t_n})) - g({X_n}))\Delta {w_n}| \le {L_2}E|{\varepsilon _n}|. $ |
C) 由引理2的2)及εn的定义得
| $ \begin{array}{l} h\theta E|f(X({t_n}) + hf(X({t_n}))) - f({X_n} + hf({X_n}))| \le h{L_2}E\\ |X({t_n}) + hf(X({t_n})) - ({X_n} + hf({X_n}))| = h{L_2}E|X({t_n}) - \\ {X_n} + h(f(X({t_n})) - f({X_n}))| \le h{L_2}E|{\varepsilon _n}| + {h^2}{L_2}E|\\ f(X({t_n})) - f({X_n})| \le h{L_2}E|{\varepsilon _n}| + {h^2}{L_2}^2E|{\varepsilon _n}| = \\ (h{L_2} + {h^2}{L_2}^2)E|{\varepsilon _n}\left| {, E} \right|{\varepsilon _{n + 1}}| \le (1 + {L_2} + (2{L_2} + {L_2}^2h)h)\\ E|{\varepsilon _n}\left| { + E} \right|{\delta _{n + 1}}| \le (1 + {L_2} + (2{L_2} + {L_2}^2)h)E|{\varepsilon _n}\left| { + E} \right|{\delta _{n + 1}}|. \end{array} $ |
记C5=2L2+L22, 显然C5>0且是与h无关的常数, 则E|εn+1|≤(1+L2+C5h)E|εn|+E|δn+1|.
反复应用上述关系可得
| $ \begin{array}{l} E|{\varepsilon _{n + 1}}| \le {(1 + {L_2} + {C_5}h)^{n + 1}}E|{\varepsilon _0}| + \\ (\mathop {\max }\limits_{0 \le n \le N} E[|{\delta _{n + 1}}|\left] ) \right[{(1 + {L_2} + {C_5}h)^n} - 1]/({L_2} + {C_5}h).{\rm{ }} \end{array} $ |
由引理3, 当ε0=0时, E|ε0|=0, 再由(1)的证明上式变为
| $ \begin{array}{l} E|{\varepsilon _{n + 1}}| = (\mathop {\max }\limits_{0 \le n \le N} E|{\delta _{n + 1}}|)[{(1 + {L_2} + {C_5}h)^n} - 1]/\\ ({L_2} + {C_5}h) \le ({C_3}{h^2}/({L_2} + {C_5}))h[{(1 + {L_2} + {C_5}h)^n} - 1]\\ \le h\frac{{{C_3}}}{{{L_2} + {C_5}}}({{\rm{e}}^{{C_5}T}} - 1) = O\left( h \right). \end{array} $ |
由引理3得p3=1, 故p4=2, 即存在不依赖于h的常数C6, 使得
对于实验方程
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{d}}X\left( t \right) = \lambda X{\rm{d}}t + \mu X{\rm{d}}w\left( t \right), }&{t \in \left[ {0, T} \right].}\\ {X\left( 0 \right) = {X_0} = 1, }&{\lambda , \mu \in {\bf{R}}.} \end{array}} \right. $ |
取
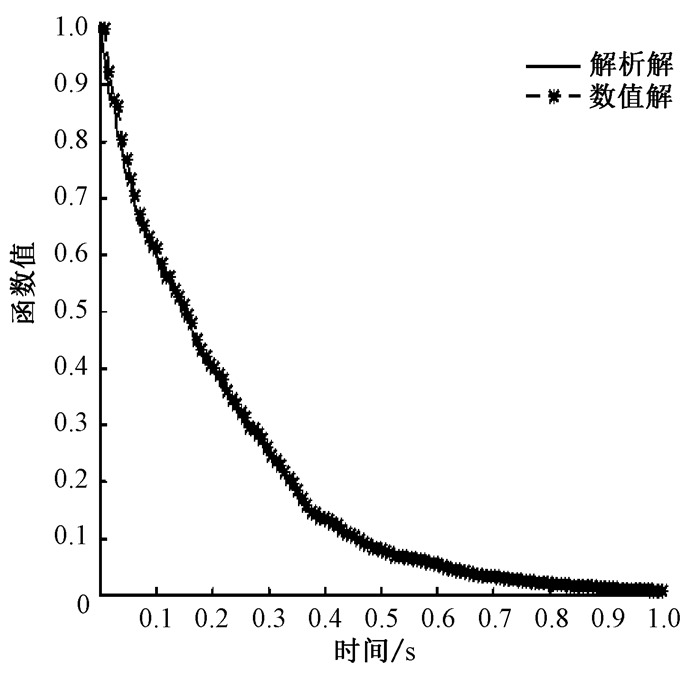
|
图 1 θ-Heun方法数值解与精确解的对比 Fig. 1 The comparison of the numerical solution of the θ-Heun method to the exact solution |
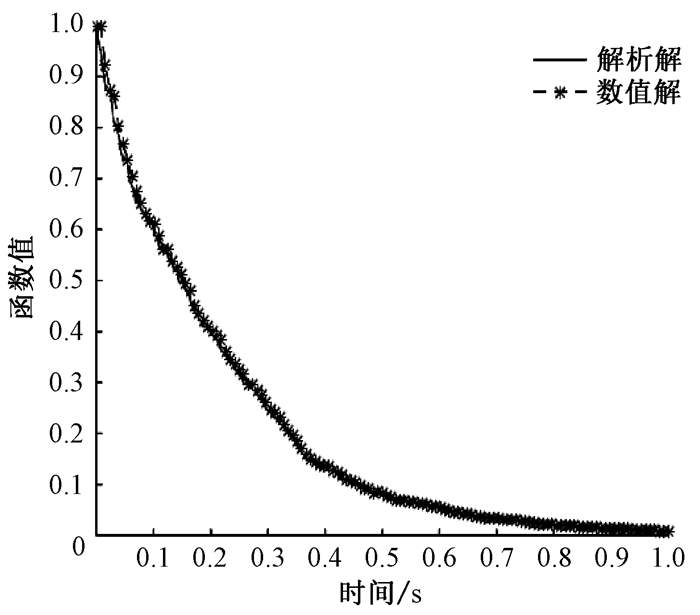
|
图 2 Heun方法数值解与精确解的对比 Fig. 2 The comparison of the numerical solution of the Heun method to the exact solution |
| [1] |
朱晓林, 徐道叁, 李井刚, 等. 求解随机微分方程Heun方法的收敛性研究[J]. 合肥工业大学学报(自然科学版), 2011, 34(12): 1907-1912. DOI:10.3969/j.issn.1003-5060.2011.12.034 (  0) 0) |
| [2] |
MARUYAMA G. Continuous Markov process and stochastic equations[J]. Rendiconti del circolo matematico di palermo, 1955, 4(1): 48-90. DOI:10.1007/BF02846028 (  0) 0) |
| [3] |
MILSTEIN G N. Approximate integration of stochastic differential equation[J]. Theory of probability and its applications, 2006, 19(3): 583-588. (  0) 0) |
| [4] |
KLOEDEN P E, PLATEN E, SCHURZ H. The numerical solution for non-linear stochastic dynamical systems: a brief introduction[J]. Journal of computational and applied mathematics, 1991, 40(1): 277-286. (  0) 0) |
| [5] |
BUCKWAR E. Introduction to the numerical analysis of stochastic delay differential equations[J]. Journal of computational and applied mathematics, 2000, 125: 297-307. DOI:10.1016/S0377-0427(00)00475-1 (  0) 0) |
| [6] |
闫振海, 刘再明, 王帅鸽, 等. 一维非线性随机微分方程的随机指数稳定性[J]. 郑州大学学报(理学版), 2015, 47(2): 20-21. DOI:10.3969/j.issn.1671-6841.2015.02.004 (  0) 0) |
| [7] |
王鹏飞, 殷凤, 蔺小林. 求解非线性随机微分方程加权格式的收敛性[J]. 郑州大学学报(理学版), 2009, 41(3): 9-10. (  0) 0) |
| [8] |
EVANS L C. An introduction to stochastic differential equations[M]. Berkeley: Amer Mathematical Society, 2014.
(  0) 0) |
| [9] |
李井刚, 朱晓林, 王子洁. 一种基于随机Taylor展开式的随机微分方程数值解法[J]. 大学数学, 2013, 29(4): 46. (  0) 0) |
| [10] |
SAITO Y, MITSUI T. Stability analysis of numerical schemes for stochastic differential equations[J]. Siam journal on numerical analysis, 1996, 33(6): 2254-2267. DOI:10.1137/S0036142992228409 (  0) 0) |
 2019, Vol. 51
2019, Vol. 51


