钝体绕流是流体力学中的复杂问题.流体绕流钝体时, 在尾流两侧会产生交替旋涡, 即卡门涡街.卡门涡街中的旋涡脱落作用会对钝体产生周期性、脉动性作用力, 如果钝体本身具有弹性或者弹性安装, 当流体力作用在钝体上时, 钝体会发生周期性的振动, 称为流致振动.通常认为流致振动是一种只有害现象, 因为当旋涡脱落的频率接近钝体的固有频率时, 会使钝体振动大幅增强, 钝体结构容易产生破坏.然而随着微能源技术的飞速发展, 研究发现涡激振动可作为一种能量转换过程, 具有实现能量收集的可能性.目前, 人们发现的实现振动机械能到电能的转化方式主要有静电式[1]、电磁式[2]和压电式[3].而流致振动进行微能量收集方法属于利用压电材料的正压电效应实现了振动机械能到电能的转化.
为了对涡激振动能量进行高效的收集, 国内外相继发展了尾流振子模型、二阶弹簧-振子模型、统计模型以及多项伽辽金求解模型[4]等数学模型.尾流振子模型[5]由于具有较为明确、合理的物理意义以及较高的计算精度, 因此得到了广泛的采用.文献[6]最早提出了尾流振子模型及其完整的数学表达式.文献[7]研究了尾流振子模型的动力特性, 发现位移和速度耦合预测升力相位关系不够准确, 位移耦合无法对锁定区升力的大小进行有效的判断.文献[8]针对张紧梁提出了用双耦合尾流振子模型来模拟2个方向上的脉动作用力.文献[9]提出了对弹性的圆柱体适用的Skop-Griffin模型, 且计算出i阶振型的数学表达式.自从微能量收集问题进入学者的视线以来, 尾流振子模型大都只停留在对圆柱体涡激振动的研究上, 而忽略了尾流振子本身对涡激振动的增强作用.本文采用压电悬臂梁结构, 结合流机电三物理场耦合方程对尾流振子涡激振动的能量收集特性进行分析, 采用数值方法研究了不同雷诺数(5 000≤Re≤15 000)下尾流振子模型的工况.详细分析了尾迹振子的升力系数、振幅率及收集到的电压随时间的变化规律, 探讨了各种因素对于尾流振子能量收集系统的影响, 并将相同雷诺数下不同尾流振子两柱间距工况进行对比, 以选择出最合适的间距.
1 物理模型直接对物体流致振动进行研究很抽象, 可以将尾迹振子的运动形象地用质量弹簧阻尼系统来模拟, 这样尾迹振子在涡激振动的脉动力作用效果等同于在弹簧弹性力的作用效果.考虑到圆柱体流致振动沿流动方向的振幅远小于横向振幅, 为了求解方便, 忽略了流动方向振动.本文采用光滑圆柱面, 尾流振子物理模型如图 1所示.取柱体直径D=0.01 m, 柱体质量为0.093 4 kg, 尾流振子间距为X, 弹簧弹性系数K=678 N/m, 系统阻尼C=0.107 N·s/m.

|
图 1 尾流振子物理模型 Figure 1 Wake oscillator physical model |
将尾流振子模型置于流场中, 假设为无边界流场, 设计的尾流振子能量收集系统如图 2所示.假设尾流振子处于1.2 m×1.0 m×0.4 m且温度恒定为20 ℃的水流场中, 工况参数如表 1所示, 其中Ur为折减速度.流速取0.8 m/s, 圆柱直径为D, 长L为1 m, 尾流振子间距为11D, 尾流振子材料选择密度为1 190 kg/m3的铝合金材料.
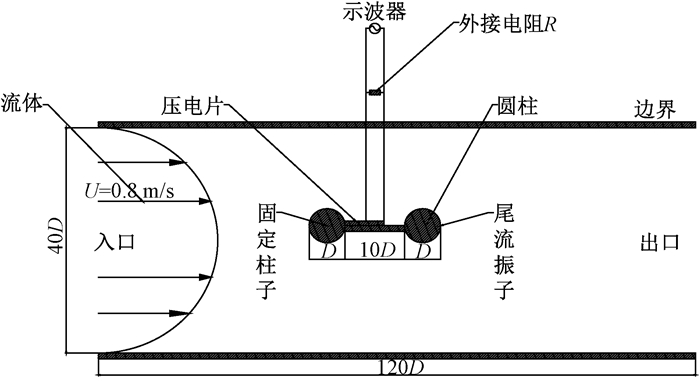
|
图 2 尾流振子能量收集系统 Figure 2 Wake oscillator energy harvesting system |
|
|
表 1 尾流振子工况参数 Table 1 Operating parameters of wake oscillator |
单自由度M-C-K系统的运动控制方程可以由二阶弹簧-振子方程表示为
| $ M\ddot y + C\ddot y + Ky = {F_y}, $ | (1) |
式中:M为系统的总质量;C为系统阻尼;K为弹性系数;y为尾部柱体的位移;Fy表示垂直于来流方向的单位体积的流场力.
将系统阻尼和临界阻尼的比值设为系统的阻尼系数ζ, 定义式为
| $ \zeta = \frac{C}{{{C_s}}} = \frac{C}{{2\sqrt {MK} }}. $ | (2) |
设系统频率为ωn, 定义式为
| $ {\omega _n} = \sqrt {\frac{K}{M}} . $ | (3) |
折减速度Ur可以表示为
| $ {U_r} = \frac{U}{{{f_n}D}}, $ |
式中:fn表示尾流振子模型的固有频率,
柱体涡激振动力等效为压电悬臂梁模型中质量块的重力, 设尾迹振子的位移为y, 结合M-C-K方程和压电悬臂梁机构电路图, 可以得到尾流振子涡激振动能量收集的机电耦合控制方程组为
| $ M\ddot y + C\ddot y + Ky - \theta v = {F_y}, $ | (4) |
| $ \theta \dot y + {C_p}V + \frac{V}{R} = 0, $ | (5) |
式中:参数θ为机电耦合系数;Cp为等效电容.
引入涡激振动系统的振动形式方程为
| $ y = {y_{\max }}\sin ({\omega _n}t + \varphi ). $ | (6) |
方程式(4)~(6)中, M、C、K、θ、Cp、R均为常数;将3个方程联立后封闭, 可求出V(t).根据功率关系式P=Vrms2/R可得到功率表达式.
2 数值方法格子Boltzmann方法是本文的一个核心计算方法, 它是从分子动理论学说出发, 基于微观粒子运动, 在介观层次对粒子建立了离散速度模型、时间和空间离散模型.再根据质量、动量和能量守恒分别建立密度、速度、内能的方程, 求出粒子分布函数, 然后用统计学的方法得到宏观的压力、流速等参数.
建立离散速度模型, 只考虑单组分气体, 然后设速度分布函数为f, f的值与空间位置矢量r(x, y, z)、分子速度矢量ξ(ξx, ξy, ξz)及时间t有关.粒子分布函数n即为t时刻r处单位体积内的分子数, 也称数密度.
速度分布函数f的改变, 可能是由分子的运动或分子的碰撞引起的.由钢球碰撞理论可得
| $ \begin{array}{l} \frac{{\partial f}}{{\partial t}} + \mathit{\boldsymbol{\xi }} \cdot \frac{{\partial f}}{{\partial \mathit{\boldsymbol{r}}}} + \mathit{\boldsymbol{a}} \cdot \frac{{\partial f}}{{\partial \mathit{\boldsymbol{\xi }}}} = \\ \smallint \smallint (f{'_1}f{'_2} - {f_1}{f_2})d_D^2|\mathit{\boldsymbol{g}}|\cos \theta {\rm{d}}\mathit{\Omega }d\mathit{\boldsymbol{\xi }}. \end{array} $ | (7) |
从Boltzmann方法到Boltzmann-BGK方程, 就是用一个简单的算子Ωf来替代碰撞项, 从而达到简化Boltzmann方程的目的.Ωf代替了Boltzmann方程右侧的碰撞项, 得出了BGK近似:
| $ {\mathit{\Omega }_f} = \nu [{f^{eq}}\left( {\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{\xi }}, t} \right) - f\left( {\mathit{\boldsymbol{r}}, \mathit{\boldsymbol{\xi }}, t} \right)]. $ | (8) |
BGK近似使得Boltzmann方程线性化, 大大简化了方程的求解.引入碰撞时间τ0, 它是粒子平均每两次碰撞的时间间隔, 也称弛豫时间, 可以表示为τ0=1/ν.
简化后的Boltzmann-BGK方程可以表示为
| $ \frac{{\partial f}}{{\partial t}} + \mathit{\boldsymbol{\xi }} \cdot \frac{{\partial f}}{{\partial \mathit{\boldsymbol{r}}}} + \mathit{\boldsymbol{a}} \cdot \frac{{\partial f}}{{\partial \mathit{\boldsymbol{\xi }}}} = - \frac{{f - {f^{{\rm{eq}}}}}}{{{\tau _0}}}. $ | (9) |
从Boltzmann-BGK方程到格子Boltzmann方程是速度离散、时间离散、空间离散的过程.
本文采用D2Q9模型, 如图 3所示.由格子Boltzmann方法得平衡态分布函数为
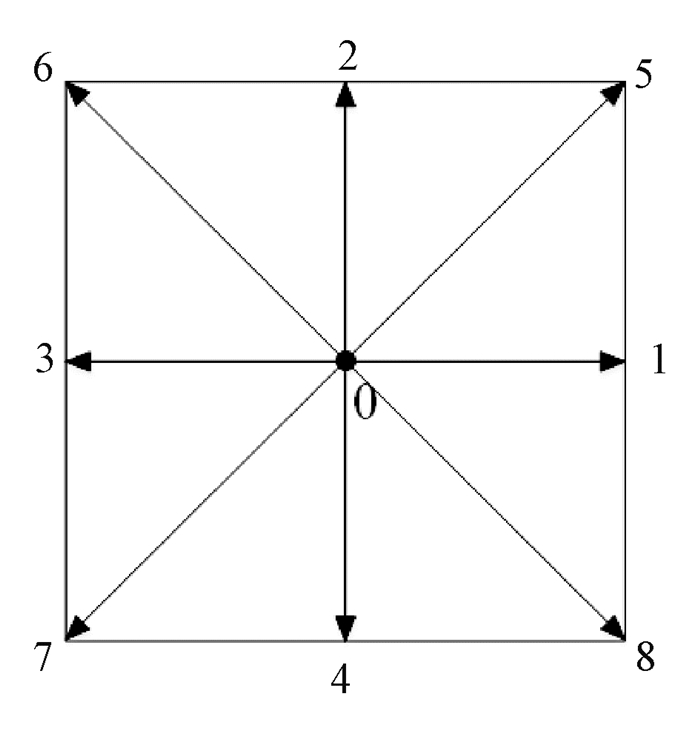
|
图 3 D2Q9模型 Figure 3 D2Q9 model |
| $ f_i^{{\rm{eq}}}\left( x \right) = {w_i}\rho \left( x \right)[1 + \frac{{{e_i} \cdot u}}{{c_s^2}} + \frac{{{{({e_i} \cdot u)}^2}}}{{2c_s^4}} - \frac{{{u^2}}}{{2c_s^2}}], $ | (10) |
式中:wi为权系数.
3 结果与讨论采用基于格子Boltzmann方法的XFlow软件对尾流振子流致振动进行数值模拟, 该方法应用范围广、效率高, 无须网格, 边界条件易于处理, 模拟精度较高.内部求解器适合完整的流固耦合分析, 计算域如图 4所示.
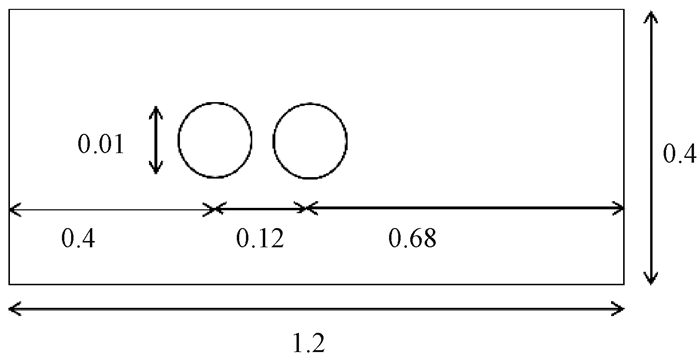
|
图 4 计算域(单位:m) Figure 4 Computational domain(unit:m) |
对于有外接电阻R的情况, 采用XFlow软件和OpenModelica进行流机电耦合计算, 由XFlow软件得到尾迹振子的升力随时间变化的数据, 再将数据输入到OpenModelica中, 通过对方程(4)、(5)的求解可得到尾流振子的振幅随时间的变化值和涡激振动产生的电压随时间的变化值.能量收集计算中, 系统机电耦合系数θ=0.000 202 2 V/N, 等效电容Cp=61.3 nF, 引入无量纲参数Ur使计算更具有普遍性, 通过改变来流速度(即流体雷诺数Re)和两柱间距来讨论随之改变的涡激振动参数及其产生的电压值, 以确定最适合能量收集的流体参数和两柱间距.
3.1 不同雷诺数下尾流振子流致振动振幅随速度的变化如图 5所示.尾流振子在速度为0.5~0.7 m/s, 即Re为5 000~7 000的条件下, 流致振动的振幅和电压的振荡幅值都比较稳定, 即为涡激振动的初始分支.而当Re为7 000~12 000时振幅显著提升, 电压振荡幅值变化较大, 即达到涡激振动的锁振范围, 用折减速度Ur表示的范围为5.16~8.84.其中Re为8 000时达到峰值, 因此尾流振子的能量收集最好能保持在雷诺数为8 000时.在Re大于13 000后, 振幅随雷诺数的变化逐渐趋于稳定, 但电压的振荡幅值更明显.此外, 随着雷诺数的增大, 尾迹振子的振动频率从5 Hz逐渐增大到15 Hz, 而系统的固有频率为13 Hz, 可知当尾流振子的振动频率接近系统的固有频率时, 系统进入锁振区域.
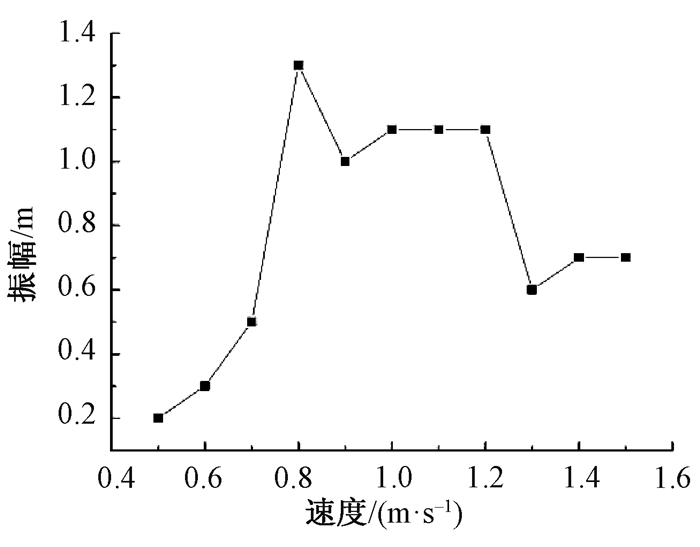
|
图 5 振幅随速度的变化 Figure 5 The changes of amplitude with velocity |
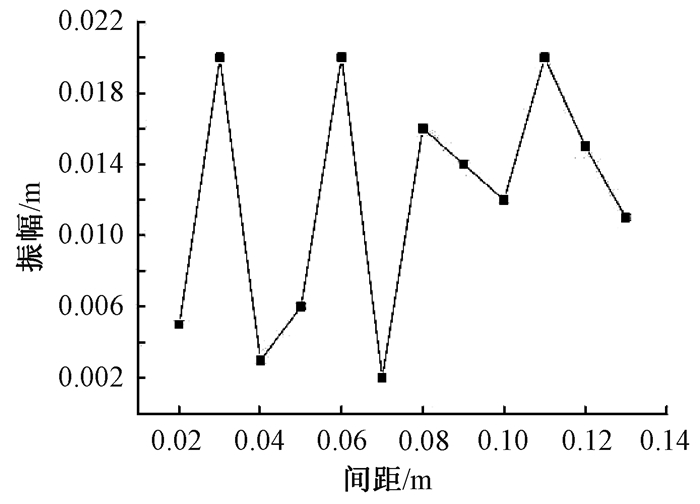
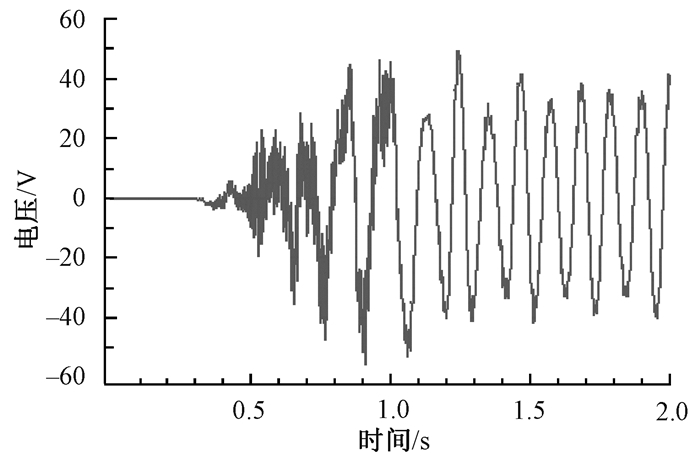
当Re为8 000时, 改变两柱间距, 对尾流振子的流致振动特性进行分析, 某时刻尾流振子尾迹旋涡形态如图 6所示, 不同间距与振幅的关系如图 7所示.可以看出, 尾流振子尾迹旋涡形态影响着间距与振幅的关系, 当两列尾迹旋涡错开时, 尾迹振子的振幅偏大;而当两列尾迹旋涡在Y轴方向相交时, 2个涡的升力相互抵消, 时间发展至此刻时, 其振幅偏小.间距为0.11 m时电压随时间的变化见图 8.如图 7、图 8所示, 在间距为0.03、0.06、0.11 m时其振幅达到峰值, 间距大于0.08 m时振幅幅值较为稳定, 且间距为0.11 m时可以得到幅值稳定为38 V的电压, 因此理想间距为0.11 m.由图 6可知, 尾流振子在涡激振动能量收集过程中, 平行于Y轴方向不被相反升力抵消的力只有一个, 此时振幅最大, 最适合能量收集.

|
图 6 Re为8 000时尾流振子尾迹旋涡形态 Figure 6 Vortex shape in wake of Re=8 000 wake oscillator |
|
图 7 不同间距与振幅的关系 Figure 7 The relation of different spacing and amplitude |
|
图 8 间距为0.11 m时电压随时间的变化 Figure 8 Voltage versus time at 0.11 m spacing |
选择压电悬臂梁结构构成尾流振子模型, 为得到更多的压电电压, 应使尾流振子模型在锁振区域内进行能量收集, 当Re为7 000~12 000时, 对应折减速度的范围为5.16~8.84.尾流振子涡激振动能量收集的最佳两柱间距为0.11 m, 可以得到38 V的稳定电压, 在电阻不变的情况下, 其得到的功率也为最大值.
| [1] |
SHEU G J, YANG S M, LEE T. Development of a low frequency electrostatic comb-drive energy harvester compatible to SoC design by CMOS process[J]. Sensors and actuators A: physical, 2011, 167(1): 70-76. DOI:10.1016/j.sna.2010.07.013 (  0) 0) |
| [2] |
ELVIN N G, ELVIN A A. An experimentally validated electromagnetic energy harvester[J]. Journal of sound and vibration, 2011, 330(10): 2314-2324. DOI:10.1016/j.jsv.2010.11.024 (  0) 0) |
| [3] |
COOK-CHENNAULT K A, THAMBI N, SASTRY A M. Powering MEMS portable devices:a review of non-regenerative and regenerative power supply systems with special emphasis on piezoelectric energy harvesting systems[J]. Smart materials and structures, 2008, 17(4): 1240-1246. (  0) 0) |
| [4] |
PRIYA S. Advances in energy harvesting using low profile piezoelectric transducers[J]. Journal of electroceramics, 2007, 19(1): 167-184. DOI:10.1007/s10832-007-9043-4 (  0) 0) |
| [5] |
HARTLEN R T, CURRIE I G. Lift-oscillator model of vortex-induced vibration[J]. Journal of the engineering mechanics division, 1970, 96(5): 577-591. (  0) 0) |
| [6] |
BISHOP R E D, HASSAN A Y. The lift and drag forces on a circular cylinder oscillating in a flowing fluid[J]. Proceedings of the royal society of London, 1964, 277(2): 51-75. (  0) 0) |
| [7] |
FACCHINETTI M L, LANGRE E D, BIOLLE Y F. Coupling of structure and wake oscillators in vortex-induced vibrations[J]. Journal of fluids and structures, 2004, 19(2): 123-140. DOI:10.1016/j.jfluidstructs.2003.12.004 (  0) 0) |
| [8] |
GE F, LONG X, WANG L, et al. Flow-induced vibrations of long circular cylinders modeled by coupled nonlinear oscillators[J]. Science in China, 2009, 52(7): 1086-1093. (  0) 0) |
| [9] |
SKOP R A, GRIFFIN O M. On a theory for the vortex-excited oscillations of flexible cylindrical structures[J]. Journal of sound and vibration, 1975, 41(3): 263-274. DOI:10.1016/S0022-460X(75)80173-8 (  0) 0) |
 2018, Vol. 50
2018, Vol. 50


