2. 河北大学 信息技术中心 河北 保定 071002
2. Information Technology Center, Hebei University, Baoding 071002, China
在社交网络数据挖掘中,研究如何实现社交网络[1]发布的原始数据集和数据集中用户隐私之间的权衡[2]已成为大数据和网络信息安全领域的热点问题。许多研究者已经相继对社交网络数据发布的隐私保护作了研究,为了减少数据发布过程中敏感信息的泄露,须对发布的数据进行处理[3],一般主要采用匿名[4-7]和差分隐私保护技术[8-9]。很多研究采用的社交网络隐私保护算法都融入了k-匿名的思想[10-13]。文献[14] 提出了一种基于k-成员模糊聚类和萤火虫算法的联合匿名算法,能有效抵御一些攻击。但是基于迭代的元启发式算法的实现,需要更长的执行时间。文献[15]提出同时考虑节点属性和结构的隐私聚类扰动算法,在顶点间随机交换属性,诱导攻击者错误的方向,采用局部聚类和边缘互补修改来扰动,使隐私得到保证。文献[16]提出(K, X)同构加权社交隐私保护,改进最大公共子图方法,以找到更合适的子图。文献[17]提出基于节点中介中心性的匿名网络重构算法,把节点按照中介中心性进行排列,具有较大值的候选节点优先进行重构。以上基于匿名算法的研究在社交网络隐私保护中都取得了较好的效果,但存在一个共同的缺陷就是在一定程度上丢失了原图的重要特征,导致信息损失,降低了网络数据效用,无法保证数据挖掘研究的有效进行。另外还有一些研究采用差分技术来保护社交网络的隐私,文献[18-19]提出了一种基于差分隐私保护多核的聚类方案,通过添加一些随机噪声来增强数据聚类效果进而保护隐私。文献[20]提出了一种差分隐私保护密度聚类的方法,把拉普拉斯噪声加入到局部密度和最短距离从而保护用户的隐私。以上采用差分聚类来保护隐私,虽然可以防御背景知识的攻击,但是数据对噪声太过敏感,小的噪声就会导致大的信息损失,从而导致数据可用性下降。针对以上不足,本文提出个性化等差数列聚类匿名分配算法(personalized arithmetic sequence clustering anonymous allocation algorithm,PAS-CAA),在保证隐私安全的前提下,实现信息损失最小化。
本文主要的贡献为:
1) 针对聚类算法存在随机选取初始节点的敏感问题,通过计算局部聚类密度参数对选取初始节点的算法进行优化,采取综合相似度进行聚类,提高聚类的有效性,同时也减少了信息的损失;
2) 在聚类过程中通过设置参数θΝ=k,使每个超点包含的个数至少为k。若不满足该条件则取消该类进行重新分配,保证每个超点都实现基本的k保护力度。把具有k保护力度的超点根据超点局部密度阈值ρθ划分为敏感超点集(ρsuper≥ρθ)和非敏感超点集(ρsuper < ρθ)。为了实现信息损失最小化,对于敏感超点集采用递减的等差数列进行聚类,使每个敏感度不同的敏感超点拥有与其相对应的隐私保护力度,其隐私保护力度范围是[2k, min[Clustervalue]]。因此,在实现最低安全隐私保护的基础上,体现个性化的隐私保护思想。
1 相关定义定义1 综合相似度,是指结构邻近相似度simstr(vi, vl) 和个人信息属性相似性simatr(vip, vlp),其中p代表属性通过调节参数β来进行调节计算出的相似度,其值越大越容易聚在一起,其中:vi、vl指的节点i和节点l; nei(vi)指节点vi的邻接节点。
| $ \begin{array}{c} S\left( {{v_i},{v_l}} \right) = \mathit{\beta si}{\mathit{m}_{{\rm{str}}}}\left( {{v_i},{v_l}} \right) + (1 - \mathit{\beta })\mathit{si}{\mathit{m}_{{\rm{atr}}}}\left( {{v_{ip}},{v_{lp}}} \right) = \\ \mathit{\beta }\left| {\mathit{nei}\left( {{v_i}} \right) \cap \mathit{nei}\left( {{v_l}} \right)} \right|/\left| {\mathit{nei}\left( {{v_i}} \right) \cup \mathit{nei}\left( {{v_l}} \right)} \right| + \\ (1 - \mathit{\beta })\sum\limits_{p = 1}^m {\mathit{si}{\mathit{m}_{{\rm{atr}}}}} \left( {{v_{ip}},{v_{lp}}} \right)/m \end{array} $ | (1) |
其中:
同理任意节点vi和超点Vx的相似度表示为
| $ S\left( {{v_i},{V_x}} \right) = \sum\limits_{{v_l} \in {V_x}} S \left( {{v_i},{v_l}} \right)/\left| {{V_x}} \right|。$ | (2) |
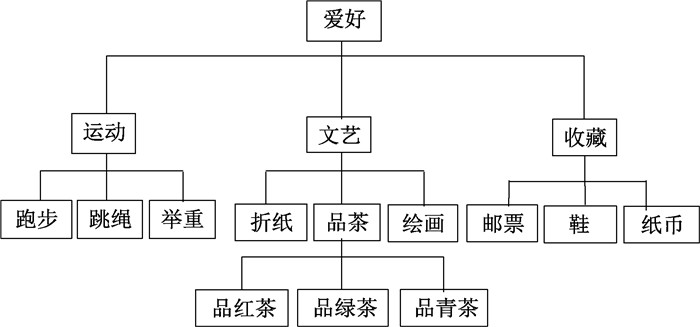
定义2 属性的概化。社交网络中的节点属性一般分为数值型和非数值型。当多个节点聚集成超点,数值型可以用[max(atr(clt)), min(atr(clt))]范围来概化超点包含的所有节点的属性值;对于非数值型可以采用泛化层次树,图 1给出一棵爱好泛化层次树,其中根节点的泛化范围最大,不同层次上的分支节点代表不同泛化范围。
|
图 1 爱好泛化层次树 Fig. 1 Hobbies generalized hierarchical tree |
定义3 局部密度ρ。给定节点vA,vAi是vA的k近邻点,节点vA的局部密度ρ的计算公式为
| $ {\mathit{\rho }_{{v_A}}} = \sum\limits_{{v_{{A_i}}} \in KNN\left( {{v_A}} \right)} {\exp } \left( { - d\left( {{v_A},{v_{{A_i}}}} \right)/\left( {{S_{NER}}\left( {{v_A},{v_{{A_i}}}} \right) + 1} \right)} \right), $ | (3) |
其中:SNER(vA, vAi)是基于k近邻聚类的共享近邻相似度,代表节点vA和vAi的近邻相似性,其值越大越容易聚在一块。同理,超点的局部密度为
| $ {\mathit{\rho }_{{\rm{super }}}} = \sum\limits_{{v_p} \in {\rm{ }}\mathit{Cluster}{\rm{ }}} {{\mathit{\rho }_{{v_p}}}} /\left| {\mathit{Cluster}} \right|。$ | (4) |
定义4 局部聚类密度Cfs(vi)是局部聚类系数,|Ni|指vi的直接邻居节点的个数,E{Ni}指节点vi的直接邻居节点构成边的个数,公式为
| $ \begin{array}{l} Cl{t_{Cc\left( {{V_i}} \right)}} = 1 + {\mathit{\rho }_{{V_i}}}*{C_{fs}}\left( {{v_i}} \right) = 1 + {\mathit{\rho }_{{v_i}}}*\left( {\left| {E\left\{ {{N_i}} \right\}} \right|/} \right.\\ \left. {\left( {\left| {{N_i}} \right|*\left( {\left| {{N_i}} \right| - 1} \right)/2} \right)} \right)。\end{array} $ | (5) |
定义5 递减的等差数列公式为
| $ \begin{array}{l} \mathit{Cluste}{\mathit{r}_{{\rm{value }}}} = 2k + (n - 1)d,\;\;\;{\kern 1pt} \;\;\;\;\;\;\;d < 0,\\ \min \left[ {\mathit{Cluste}{\mathit{r}_{{\rm{value }}}}} \right] = \left\{ {\begin{array}{*{20}{l}} {{\mathop{\rm int}} [3k/2] + 1,}&{3k\,\bmod \,2 \ne 0,}\\ {3k/2,}&{3k\,\bmod \,2 = 0,} \end{array}} \right. \end{array} $ | (6) |
其中:k是隐私保护力度;d指的是公差,根据敏感超点集隐私保护程度设定;min[Clustervalue]代表在敏感超点集中最小的隐私保护强度; 2k为首项,代表敏感超点集中敏感度最高的超点的隐私保护力度,若3k/2有余数时,min[Clustervalue]等于3k/2取整加1,反之则取3k/2。
2 基于个性化等差数列聚类匿名分配算法基于个性化等差数列聚类匿名分配算法(PAS-CAA)主要由三部分组成。首先利用初始节点优化算法选出初始节点;然后利用相似矩阵算法把每个节点与初始节点的相似度计算出来形成矩阵;最后采用PAS-CAA算法根据该相似矩阵把节点分配到初始节点形成的簇中,若形成的簇中的个数小于k,则取消该簇, 把该簇中的节点重新分配聚类,然后根据局部密度阈值ρθ,把形成的超点分成敏感超点集和非敏感超点集,让所有非敏感超点集都形成k保护力度,而作为敏感超点集, 需要更强的个性化保护,采取的保护强度范围为[2k, min[Clustervalue]],并根据敏感超点集中超点局部密度ρsuper进行由高到低排序,用公式(6)递减的等差数列进行聚类分配,最后对每个超点进行匿名化处理。实现了可以根据超点隐私要求来灵活地提供隐私保护力度,从而最大程度上减少信息损失,提高数据的利用率。
2.1 初始节点的优化算法由于K-means算法存在一定的局限性,对随机选取初始节点敏感,因此利用局部密度和局部聚类系数相结合来选择初始中心点,采用综合相似度进行聚类,实现更准确有效的聚类效果。按局部聚类密度对所有的节点进行排序,首先选取局部聚类密度最大的一个节点作为初始点,同时需要满足聚类的特性就是簇内的节点尽量紧密连在一起或相似,不同簇中的节点尽量远离或不同,所以第二个初始节点要选一个与第一个初始节点相似度最小,并且还要使局部聚类密度相对较大的节点。
算法1 初始节点优化算法。
输入:G(V, E, A),聚类个数Nc。
输出:初始中心节点。
Step1 根据公式(5)计算局部聚类密度,获取高聚集密度区域,得到集合HighCltCc;
Step2 选取局部聚类密度最大的节点作为第一个初始中心seed1;
Step3 在集合HighCltCc中选取与seed1相似度最小的点形成一个集合,并在该集合中选取局部聚类密度最大的点作为seed2;
Step4 以此类推,初始中心点的计算方法为
| $ \begin{array}{c} \mathit{See}{\mathit{d}_{{N_c}}} = \max \left( {\min \left( {\sum\limits_{i = 1}^{{N_c} - 1} S \left( {{v_l},{\rm{ }}\mathit{See}{\mathit{d}_i}} \right)} \right)} \right),\\ {v_l} \in \mathit{High}Cl{t_{{C_c}}}; \end{array} $ |
Step5 选出初始中心节点。
2.2 个性化等差数列聚类匿名算法在聚类过程中,设置参数θΝ=k, 保证了每个超点都符合最基本的k保护力度,通过ρθ局部密度阈值划分成两个区域,敏感超点集和非敏感超点集。根据超点局部密度对敏感超点集中的超点进行一个由高到低的排序,为减少信息的损失,采取递减的等差数列进行聚类,从而可以灵活地根据所需要的隐私保护来实现不同程度的保护力度,在敏感超点集中设定了隐私保护力度最大值为2k,并根据公式(6)计算敏感超点所对应的保护力度,范围为[2k, min[Clustervalue]]。当采用递减的等差数列进行聚类时,若敏感超点集的隐私保护力度小于min[Clustervalue],为了保证足够的隐私安全,该超点及之后的超点就进行保护力度为min[Clustervalue]的聚类,该方法保证最低隐私安全程度的同时,实现了个性化的隐私保护,使得需要高隐私保护要求的簇达到隐私要求的同时减少信息损失,需要低隐私保护的簇在实现数据安全性的同时保护隐私。
算法2 计算相似矩阵。
输入:用户集Nn、属性集Am、初始节点SeedNc。
输出:有序相似矩阵HT。
Step1 对于每个节点,利用公式(1)计算该节点和各个SeedNc之间的相似度;
Step2 把计算出的第一个节点和各个SeedNc的相似度放在矩阵的第一列,并用D1表示;
Step3 同理分别把各个节点与各个SeedNc算出的相似度用Dn表示;
Step4 最后形成大小为1*nNc的矩阵HT=(D1 D2 … Dn)。
算法3 PAS-CAA算法。
输入:原始社交网络图G,聚类个数Nc。
输出:社交网络图G*=(V*, E*, A*)。
Step1 通过算法1选出Nc个初始中心, 再把初始中心分配到每个簇中形成μ={μ1,μ2,…,μNc};
Step2 利用算法2计算相似矩阵HT;
Step3 把未分配的节点根据公式(2)相似度的大小分配到簇中;
Step4 判断每个簇中的元素个数是否小于θΝ (θΝ代表聚类中的最小节点数,为实现k隐私保护力度,θΝ=k), 若小于θΝ就要取消该类,Nc=Nc-1, 把取消的这个类中的节点重新分配,根据S(vi, VX)相似度的大小来分配到相应的簇中;
Step5 针对所形成的超点,计算超点的局部密度ρsuper,超点的局部密度≥ρθ(局部密度阈值),该超点归到敏感超点集中,反之放在非敏感超点集中;
Step6 非敏感超点集中节点个数大于k的超点中|Cluster| ≥k & min[S(vi, Vx)]的节点放在集合A中;
Step7 把敏感超点集中的超点根据ρsuper进行由高到低的排序;
Step8 根据步骤7中敏感超点由高到低的排序,依次利用max[S(vi, Vx)]把集合A中的点分配到敏感超点集的超点中,敏感度最高的超点采用2k隐私保护力度,然后利用公式(6)进行递减的等差数列聚类分配;
Step9 达到最大迭代数Im则终止,否则返回到Step3;
Step10 对每个超点进行匿名化(属性概化)处理;
Step11 得到聚类结果G*=(V*, E*, A*)。
3 算法分析 3.1 时间复杂度根据算法1算出所有节点的局部聚类密度,并在高聚集密度区域形成一些种子节点集,外层是簇的个数,内层是高聚集密度区域循环,因此算法1的时间复杂度是O(n2)。算法2计算相似矩阵,求解综合相似度是在O(l)中完成,所以时间复杂度是O(n2)。算法3把待分配节点都分配到簇中,外层是未分配节点数目的循环,内层是簇个数的循环,且簇个数小于等于n/k,所以时间复杂度是O(n2);同理,算法3把A集合中的节点分配到敏感超点集中未满足隐私保护力度的超点中,A集合的节点小于n,未满足匿名程度簇个数小于n/k,分配方法相同,时间复杂度也相同为O(n2);算法3对属性概化的时间复杂度是O(n2)。综上所述,本文算法的时间复杂度是O(n2)。
3.2 安全性PAS-CAA算法根据综合相似性度进行聚类,形成超点,每个超点至少有k个节点,用超点内的节点个数及边数来代替各个子图的具体结构,把超点内、超点之间节点的连接程度和子图的结构进行隐匿,可以抵御结构攻击;用超点的泛化值代替其内部各个节点的属性值,可以防止拥有属性背景知识的攻击。同时,考虑到敏感程度不同的超点对于隐私保护需求不一致,因此,需要不同的隐私保护强度,根据局部密度阈值ρθ,把超点分为敏感超点集和非敏感超点集,对于隐私要求最高的敏感超点采用2k隐私保护强度进行保护,随着隐私要求不断下降的敏感超点采用递减的等差数列进行隐私保护,直到敏感超点实现的隐私保护力度小于min[Clustervalue],代表隐私保护力度再低就不能保证敏感超点的隐私安全,所以该敏感超点及之后的敏感超点采用隐私强度为min[Clustervalue]进行聚类,因此隐私保护力度范围是[2k,min[Clustervalue]],使敏感超点集中所有超点隐私保护力度都大于等于1.5k,避免降低高隐私保护力度节点的安全性;对于非敏感超点集采用的隐私保护力度为k,使攻击者识别概率最高只能到1/k。最后,对所有超点进行匿名化处理。隐匿、泛化和个性化的等差数列聚类形成了多重的隐私保护,因此具有很强的保护效果。
3.3 有效性有效性指的是在保证隐私不被泄露的同时要减少信息损失实现数据的可用性,信息损失越少,代表数据的可用性越高。采用PAS-CAA算法进行聚类时,遵循综合相似度最大原则,即综合相似度越大的两个节点聚在同一个簇中,信息损失就越少。同理,节点与簇聚类也是遵循综合相似度最大原则,因此信息损失最少。同时把聚类以后的超点划分成非敏感超点集和敏感超点集,对于非敏感超点集中的超点,需要的隐私保护程度较低,因此用k保护力度就可以保持基本安全,避免隐私保护力度过大导致低隐私需求的超点损失更多信息的弊端;对于敏感超点集采用递减等差数列进行聚类,使需要的隐私保护力度和要求的隐私程度相符合,可以灵活有效地调节隐私保护力度,减少信息损失。总之,使得信息损失最小化,因此,具有较高的有效性。
4 实验验证实验采用Windows 10(64位),处理器是Intel(R) Core(TM) i5-6200U CPU@2.3 GHz 2.40 GHz, RAM为4.00 GB的主机。
4.1 数据集实验目的是实现隐私保护的同时使社交网络数据拥有好的可用性。实验数据来自UC Irvine Machine Learning Repository的Adult数据集,分别从中任意取500个节点和700个节点构成社交网络,记为M1和M2,利用Python3在两个真实数据集上比较PAS-CAA算法、经典聚类匿名算法SaNGreeA[21]、CAA-VS算法[22]和Adaptive-Dense-Cfs算法[23]的总体信息损失和消耗的时间。
4.2 实验结果分析实验比较上述算法在数据集上的总体信息损失。信息损失包括个人属性和结构损失,个人属性损失包括数值和非数值损失,结构损失包括超点内部损失和簇之间的损失。
个人属性损失为
| $ \begin{array}{l} \mathit{Sum\_los}{\mathit{s}_{{\rm{inf }}}}{\rm{ = }}\sum\limits_{{i = 1}}^{\rm{t}} {\sum\limits_{{L = 1}}^{\rm{m}} {\left( {\mathit{los}{\mathit{s}_{{\rm{inf }}}}\left( {\mathit{cl}{\mathit{t}_\mathit{i}},\mathit{L}} \right)} \right)} } {\rm{/}}\mathit{n}{\rm{ = }}\\ \sum\limits_{i = 1}^t {\sum\limits_{L = 1}^m {\frac{{\left| {cl{t_i}} \right|*\left( {\max \left( {\mathit{at}{\mathit{r}_{Lj}}} \right) - \min \left( {at{r_{Lj}}} \right)} \right)}}{{\left( {\max \left( {at{r_{L\left( {cl{t_i}} \right)}}} \right) - \min \left( {at{r_{L\left( {cl{t_i}} \right)}}} \right)} \right)/n}}} } {\rm{,}}\;\;\;\;{\rm{数值型,}} \end{array} $ | (7) |
| $ \begin{array}{l} \mathit{Sum\_los}{\mathit{s}_{{\rm{inf }}}}{\rm{ = }}\sum\limits_{{\rm{i = 1}}}^{\rm{t}} {\sum\limits_{{\rm{L = 1}}}^{\rm{m}} {\left( {\mathit{los}{\mathit{s}_{{\rm{inf}}}}\left( {\mathit{cl}{\mathit{t}_\mathit{i}},\mathit{L}} \right)} \right)} } {\rm{/}}\mathit{n}{\rm{ = }}\\ \sum\limits_{i = 1}^t {\sum\limits_{L = 1}^m {\sum\limits_{{v_p} \in cl{t_i}} {\left( {{\rm{length}}\left( {\mathit{at}{\mathit{r}_{Lp}},atr_{Lp}^*} \right)} \right)} } } /\\ {\rm{(length}}\left. {\left( {\mathit{at}{\mathit{r}_{Lp}},\mathit{root}} \right)} \right)/n,\;\;\;{\kern 1pt} {\rm{非数值型}} \end{array} $ | (8) |
其中:n指的是节点的个数;clt={clt1, clt2, clt3,…, cltt}为匿名后的社交网络;clti={v1, v2, v3, …, vj}, atrLj代表节点vj在属性L上的值。
结构损失为
| $ \begin{array}{l} \mathit{Sum\_los}{\mathit{s}_{{\rm{str}}}}{\rm{ = }}(\sum\limits_{{\rm{i = 1}}}^{\rm{t}} {\mathit{Los}{\mathit{s}_{{\rm{str}}}}} \left( {\mathit{cl}{\mathit{t}_\mathit{i}}} \right){\rm{ + }}\\ \sum\limits_{i = 1}^t {\sum\limits_{j = i + 1}^t {\mathit{Los}{\mathit{s}_{{\rm{str}}}}} } (cl{t_i},cl{t_j}))/(n*(n - 1)/4) = \\ (\sum\limits_{i = 1}^t {((\frac{{\left| {cl{t_i}} \right|}}{2}) - \left| {{E_{cl{t_i}}}} \right|)} *(\left| {{E_{cl{t_i}}}} \right|/(\frac{{\left| {cl{t_i}} \right|}}{2})) + \\ \left| {{E_{cl{t_i}}}} \right|*(1 - (\left| {{E_{cl{t_i}}}} \right|/(\frac{{\left| {cl{t_i}} \right|}}{2}))) + \\ \sum\limits_{i = 1}^t {\sum\limits_{j = i + 1}^t 2 } *\left| {{E_{cl{t_i},cl{t_j}}}} \right|*(1 - (\left| {{E_{cl{t_i},cl{t_j}}}} \right|/\\ (\left| {cl{t_i}} \right|*\left| {cl{t_j}} \right|))))/(n*(n - 1)/4) \end{array} $ | (9) |
总体信息损失为
| $ \mathit{Sum\_loss}{\rm{ = }}\left( {\mathit{Sum\_los}{\mathit{s}_{{\rm{inf }}}}{\rm{ + }}\mathit{Sum\_los}{\mathit{s}_{{\rm{str }}}}} \right){\rm{/2}}。$ | (10) |
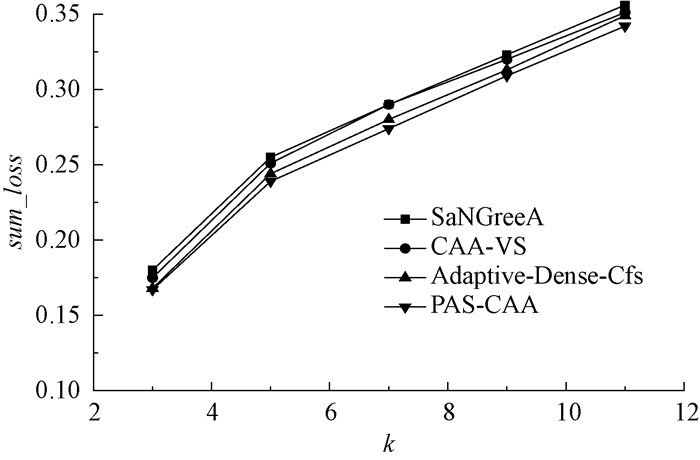
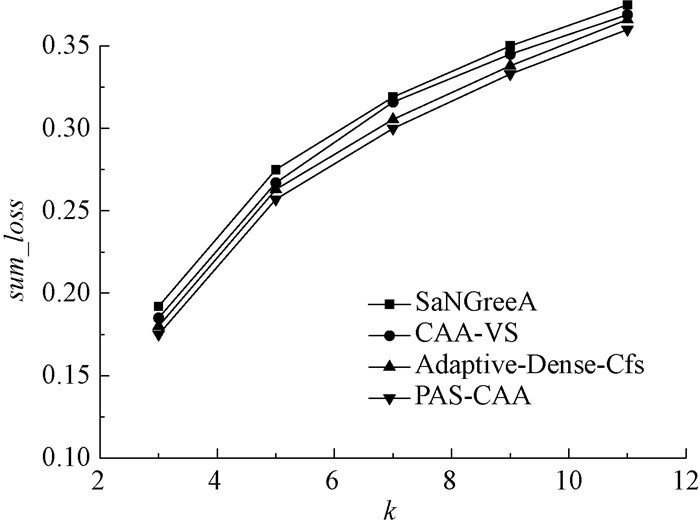
实验在数据集M1和M2上的总体信息损失结果分别如图 2、图 3所示。从图 2和图 3中可以看出,随着簇中节点数(隐私保护力度)k的增大,隐匿性自然会越好,总体信息损失也会增大,因为会有更多的节点和边及其结构被隐匿,并且每个超点的泛化范围也会变大,导致总体信息损失变大。同时图 2和图 3的sum_loss比较接近,因为sum_loss代表总的平均信息损失,但是总体看来图 3的总体信息损失相对较大,因为数据集的增大会按比例使簇中不同类型的属性值更大程度被隐匿。PAS-CAA算法比其他算法有着较低的总体信息损失,因为PAS-CAA算法把超点划分成非敏感超点集和敏感超点集,对敏感超点集采用递减等差数列进行聚类分配,在隐私保护力度为[2k, min[Clustervalue]]中可以进行动态个性化聚类分配,使隐私要求与保护程度贴切,避免使用相同的隐私保护力度导致与实际需求的保护力度不一致,从而减少总体信息损失,对于非敏感超点集进行k保护力度聚类,保证了最低隐私安全。所以PAS-CAA算法总体信息损失最小,更具有数据有效性。
|
图 2 在M1下总体信息损失比较 Fig. 2 Comparison of sum_loss under M1 |
|
图 3 在M2下总体信息损失比较 Fig. 3 Comparison of sum_loss under M2 |
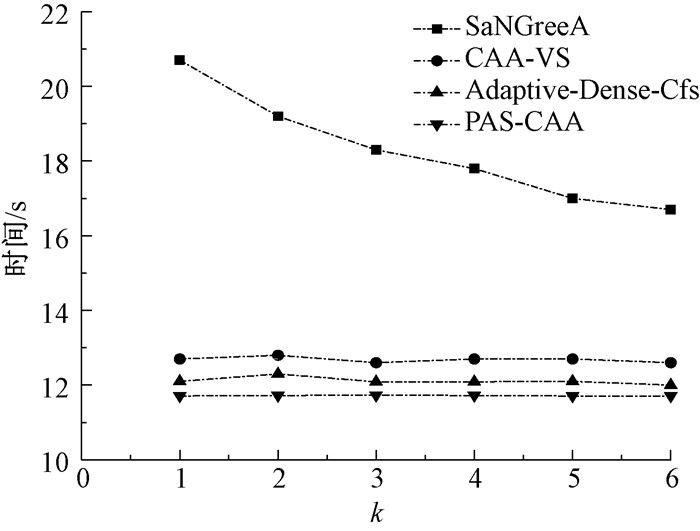
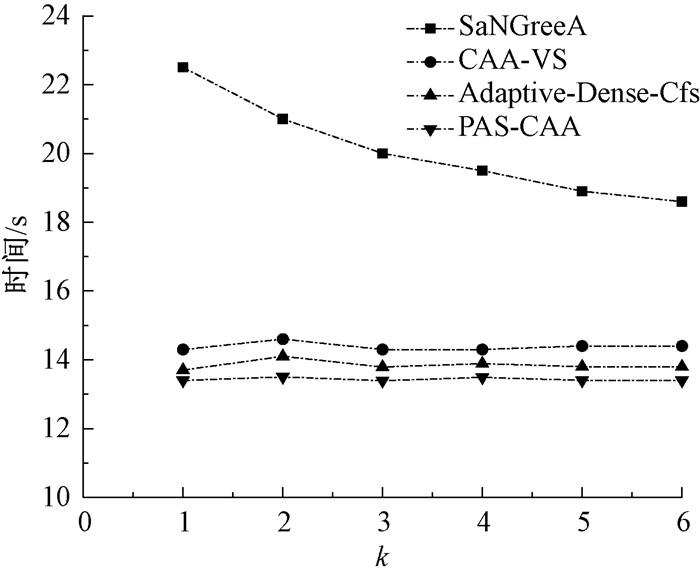
如图 4和图 5所示,在数据集M2上比M1上用的时间多,因为数据越多,就需要越多的时间处理。PAS-CAA算法避免进行多余的聚类分配来实现比实际需求高的隐私保护力度,从而时间最少、效率最高。因此PAS-CAA算法的时间变化率基本为0,不随k的变化而变化。
|
图 4 在M1下时间比较 Fig. 4 Time comparison under M1 |
|
图 5 在M2下时间比较 Fig. 5 Time comparison under M2 |
针对社交网络数据的急剧增加不能实现隐私保护力度和数据可用性平衡的问题,提出了PAS-CAA算法,对K-means没有结合社交网络的特点和初始节点选择敏感的问题进行了改进。利用局部聚类密度来选择初始中心节点,根据综合相似性进行更加准确地聚类,减少信息的损失,使得每个簇中至少包括k个节点,并且根据超点有着不同程度的隐私需求,分成了敏感超点集和非敏感超点集,对敏感超点集采用等差数列进行聚类分配,从而可以不断地根据敏感超点所需的隐私要求进行相应的隐私保护。在未来的工作中,要设计抵御一切背景知识攻击的差分聚类算法,采用准确聚类的动态分配隐私预算的方法,使得可以根据用户的隐私保护要求进行更加准确地分配,提高聚类结果的准确性和效率,同时提高差分聚类后数据的实用性。
| [1] |
ARAFEH M, CERAVOLO P, MOURAD A, et al. Ontology based recommender system using social network data[J]. Future generation computer systems, 2021, 115: 769-779. DOI:10.1016/j.future.2020.09.030 (  0) 0) |
| [2] |
PENG S C, YU S, MUELLER P. Social networking big data: Opportunities, solutions, and challenges[J]. Future generation computer systems, 2018, 86: 1456-1458. DOI:10.1016/j.future.2018.05.040 (  0) 0) |
| [3] |
王明月, 张兴, 李万杰, 等. 面向数据发布的隐私保护技术研究综述[J]. 小型微型计算机系统, 2020, 41(12): 2657-2667. WANG M Y, ZHANG X, LI W J, et al. Review of research on privacy protection technology for data publication[J]. Journal of Chinese computer systems, 2020, 41(12): 2657-2667. DOI:10.3969/j.issn.1000-1220.2020.12.031 (  0) 0) |
| [4] |
SAMARATI P, SWEENEY L. Protecting privacy when disclosing information: k-anonymity and its enforcement through generalization and suppresion[R]. Technical Report, SRI International, 1998: 384-393.
(  0) 0) |
| [5] |
GACHANGA E, KIMWELE M, NDERU L. Feature based data anonymization with slicing method for data publishing[C]//Proceedings of the 2019 11th International Conference on Machine Learning and Computing. Zhuhai: ACM press, 2019: 274-279.
(  0) 0) |
| [6] |
PATIL D, MOHAPATRA R K, BABU K S. Evaluation of generalization based K-anonymization algorithms[C]//2017 Third International Conference on Sensing, Signal Processing and Security (ICSSS). Chennai: IEEE, 2017: 171-175.
(  0) 0) |
| [7] |
程楠楠, 刘树波, 熊星星, 等. 用于敏感属性保护的(θ, k)-匿名模型[J]. 郑州大学学报(理学版), 2019, 51(03): 42-47. CHENG N N, LIU S B, XIONG X X, et al. A (θ, k)-anonymous model for sensitive attributes protection[J]. Journal of Zhengzhou university (natural science edition), 2019, 51(3): 42-47. (  0) 0) |
| [8] |
Dwork C. Differential privacy[C]//33rd International Colloquium on Automata, Languages and Programming. Venice: Springer, 2006: 1-12.
(  0) 0) |
| [9] |
NING B, SUN Y H, TAO X Y, et al. Differential privacy protection on weighted graph in wireless networks[J]. Ad hoc networks, 2021, 110: 102303. DOI:10.1016/j.adhoc.2020.102303 (  0) 0) |
| [10] |
ZHANG M M, QIN S J, GUO F Z. Satisfying link perturbation and k-out anonymous in social network privacy protection[C]//2017 IEEE 17th International Conference on Communication Technology (ICCT). Chengdu: IEEE Press, 2017: 1387-1391.
(  0) 0) |
| [11] |
YUAN J, OU Y Y, GU G S. An improved privacy protection method based on k-degree anonymity in social network[C]//2019 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA). Dalian: IEEE Press, 2019: 416-420.
(  0) 0) |
| [12] |
LIU P, BAI Y, WANG L, et al. Partial k-anonymity for privacy-preserving social network data publishing[J]. International journal of software engineering and knowledge engineering, 2017, 27(1): 71-90. DOI:10.1142/S0218194017500048 (  0) 0) |
| [13] |
SIDDULA M, CAI Z P, MIAO D J. Privacy preserving online social networks using enhanced equicardinal clustering[C]//2018 IEEE 37th International Performance Computing and Communications Conference (IPCCC). Orlando: IEEE Press, 2018: 1-8.
(  0) 0) |
| [14] |
LANGARI R K, SARDAR S, AMIN MOUSAVI S A, et al. Combined fuzzy clustering and firefly algorithm for privacy preserving in social networks[J]. Expert systems with applications, 2020, 141: 112968. DOI:10.1016/j.eswa.2019.112968 (  0) 0) |
| [15] |
YU F H, CHEN M J, YU B L, et al. Privacy preservation based on clustering perturbation algorithm for social network[J]. Multimedia tools and applications, 2018, 77(9): 11241-11258. DOI:10.1007/s11042-017-5502-3 (  0) 0) |
| [16] |
AL-KHARJI S, TIAN Y, AL-RODHAAN M. A novel (K, X)-isomorphism method for protecting privacy in weighted social network[C]//2018 21st Saudi Computer Society National Computer Conference (NCC). Riyadh: IEEE Press, 2018: 1-6.
(  0) 0) |
| [17] |
TIAN H, LU Y, LIU J T, et al. Betweenness centrality based k-anonymity for privacy preserving in social networks[C]//Proceedings of the 16th International Conference on Advances in Mobile Computing and Multimedia. Yogyakarta: ACM Press, 2018: 3-7.
(  0) 0) |
| [18] |
NI L N, LI C, WANG X, et al. DP-MCDBSCAN: differential privacy preserving multi-core DBSCAN clustering for network user data[J]. IEEE access, 2018, 6: 21053-21063. DOI:10.1109/ACCESS.2018.2824798 (  0) 0) |
| [19] |
NI L N, LI C, LIU H R, et al. Differential private preservation multi-core DBScan clustering for network user data[J]. Procedia computer science, 2018, 129: 257-262. DOI:10.1016/j.procs.2018.03.073 (  0) 0) |
| [20] |
SUN L P, BAO S T, CI S, et al. Differential privacy-preserving density peaks clustering based on shared near neighbors similarity[J]. IEEE access, 2019, 7: 89427-89440. DOI:10.1109/ACCESS.2019.2927308 (  0) 0) |
| [21] |
CAMPAN A, TRUTA T M. Data and structural k-anonymity in social networks[C]//ACM 2008 SIGKDD international conference on knowledge discovery and data mining. Las Vegas: ACM Press, 2008: 33-54.
(  0) 0) |
| [22] |
姜火文, 占清华, 刘文娟, 等. 图数据发布隐私保护的聚类匿名方法[J]. 软件学报, 2017, 28(9): 2323-2333. JIANG H W, ZHAN Q H, LIU W J, et al. Clustering-anonymity approach for privacy preservation of graph data-publishing[J]. Journal of software, 2017, 28(9): 2323-2333. (  0) 0) |
| [23] |
周艺华, 张冰, 杨宇光, 等. 基于聚类的社交网络隐私保护方法[J]. 计算机科学, 2019, 46(10): 154-160. ZHOU Y H, ZHANG B, YANG Y G, et al. Cluster-based social network privacy protection method[J]. Computer science, 2019, 46(10): 154-160. DOI:10.11896/jsjkx.180901749 (  0) 0) |
 2022, Vol. 54
2022, Vol. 54


