虹膜识别是指利用人眼虹膜区域进行身份鉴别的技术.虹膜因其可采集性、稳定性、唯一性及非侵犯性等优点逐步受到人们的重视,已发展成为主流的生物特征识别手段.它以快速的识别率、简单的算法和极低的错误识别率逐渐应用到如电子商务、身份识别、考勤、数据加密等一些领域.传统经典的虹膜识别方法主要有:Daugman提出的基于Gabor滤波的方法,从定位出的虹膜图像中提取虹膜纹理相位信息进行编码,进而通过Hamming距离进行匹配的虹膜识别算法[1]; Boles提出了基于小波变换过零点的算法,提取虹膜图像过零点的点作为特征向量,使用相似度进行匹配[2]; Wildes等采用高斯-拉普拉斯金字塔获得不同分辨率的虹膜纹理图,根据相关系数进行匹配[3].
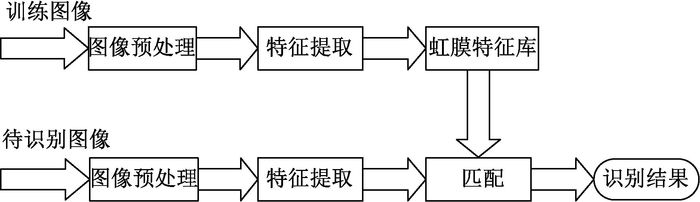
本文采用的虹膜识别算法是基于改进的SIFT算法,提取虹膜区域的纹理特征,利用街区距离进行匹配,实验结果表明该算法在保持原算法鲁棒性的同时,提高了匹配的速度.本文虹膜算法系统框图如图 1所示.
|
图 1 虹膜算法系统 Figure 1 System of iris algorithm |
虹膜识别算法能够在高质量的图像中提取到足够多的虹膜特征,使得在模式匹配阶段有较高的识别率,所以虹膜图像的采集一定程度上决定了虹膜识别率.但是由于虹膜本身的面积较小,直径约为22 mm,在图像采集过程中易受到各种因素的干扰,使采集到的虹膜图像有眼皮遮盖、偏移、光斑、旋转及睫毛干扰等现象,进而影响虹膜特征提取,降低虹膜的识别率,所以虹膜图像采集技术是虹膜识别的关键技术之一.由于虹膜采集的环境要求高以及设备的复杂性,本文只对虹膜识别的算法进行研究.
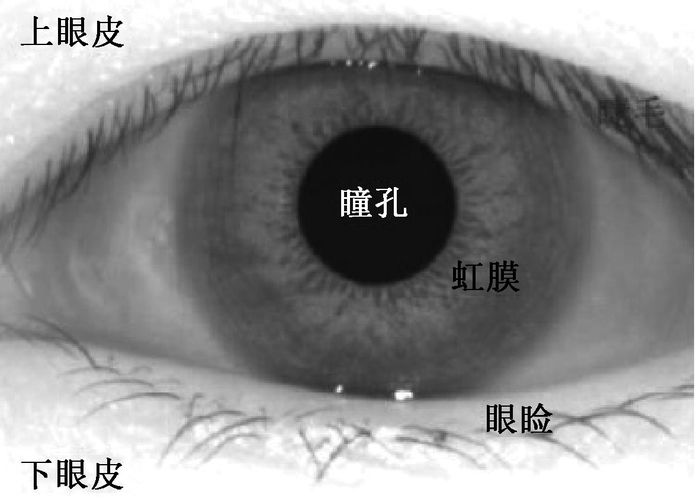
2 虹膜图像预处理一般情况下,采集到的虹膜图像中不仅有虹膜,还包括睫毛、眼睑、瞳孔及巩膜等,如图 2所示.因此,需要将虹膜从图像中定位出来.
|
图 2 虹膜图像 Figure 2 Iris image |
虹膜图像预处理包括虹膜图像定位分割、归一化和图像增强三部分.传统的虹膜识别算法需要将定位分割后的虹膜图像进行归一化后再进行特征提取,以消除虹膜图像的光照变化、旋转、平移对特征提取的影响.由于本文采用的SIFT算法提取虹膜特征对平移、旋转等不受影响,因此可以直接在虹膜图像分割定位的基础上提取虹膜特征,即省去了归一化这一环节.
2.1 虹膜图像定位分割虹膜图像的定位分割是在采集到的虹膜图像I(x, y)上确定虹膜与瞳孔边界以及虹膜与巩膜边界,即虹膜内边界圆心及半径(xinner, yinner, rinner)和外边界圆心及半径(xouter, youter, router),根据得到的内外边界进行图像分割,得到只含有虹膜纹理的近似环形图像.
虹膜内边界定位采用人眼灰度特征与投影法相结合的虹膜快速定位方法[4],步骤如下:
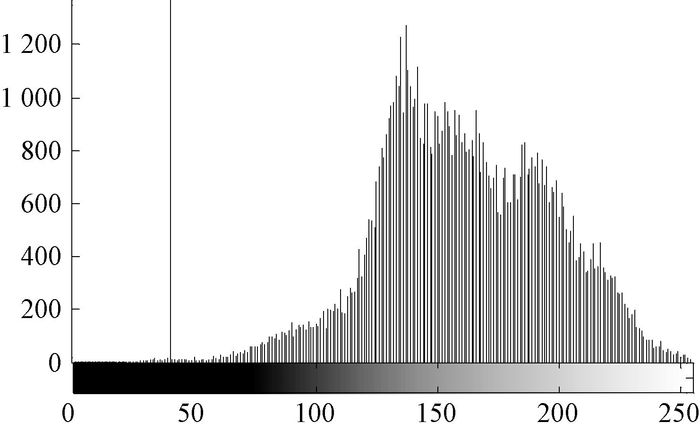
1) 建立虹膜图像I(x, y)灰度直方图,如图 3所示.找出图像中第一个峰值的灰度值,作为分割出瞳孔与虹膜的二值化阈值后对整个图像进行二值化.
|
图 3 虹膜图像的灰度直方图 Figure 3 Gray histogram of iris image |
2) 对虹膜的二值化图像进行膨胀腐蚀处理后的虹膜图像,如图 4所示.

|
图 4 二值化和膨胀腐蚀后的虹膜图像 Figure 4 Binarization of iris image after expansion and corrosion |
3) 得到瞳孔图像后运用投影法确定瞳孔的圆心和半径(xinner, yinner, rinner).
虹膜内外边界并不是真正的同心圆,但二者圆心距离很近,可根据定位出来的内边界的圆心参数(xinner, yinner), 在(xinner±2.5, yinner±2.5) 范围内搜索外边界的圆心并确定其圆心.
利用微积分算子的离散形式来进行圆的检测[5],其离散形式为
| $\text{ma}{{\text{x}}_{(n\Delta r,\text{ }{{x}_{0}},\text{ }{{y}_{0}})}}\left| \frac{1}{\Delta r}\sum\limits_{k}{\left\{ {{G}_{\sigma }}\left( r \right)\sum\limits_{m}{I\left( x,\text{ }y \right)} \right\}} \right|.$ |
其中:(x0, y0)为虹膜内边界的圆心;Gσ(r)=Gσ((n-k)Δr)-Gσ((n-k-1)Δr);
图 5为采用文中定位内外边界方法处理后的效果图.
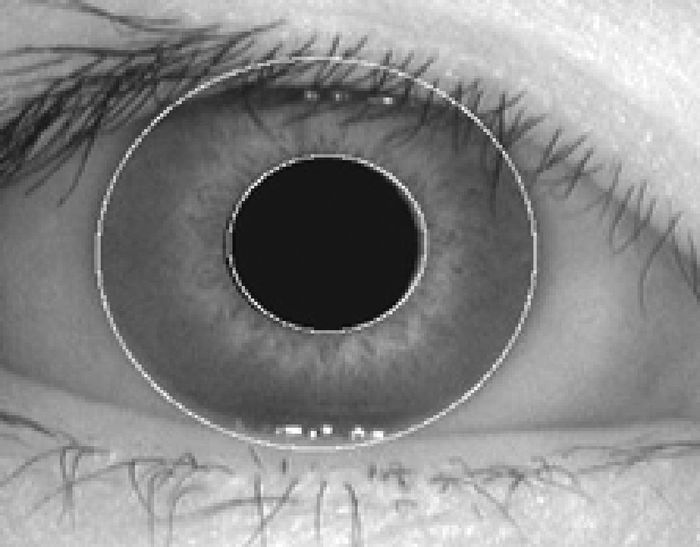
|
图 5 定位后的虹膜图像 Figure 5 Iris image after location |
SIFT算法是在多尺度空间提取位置、尺度及旋转不变量等特征点的过程[6-7].该算法可以提取到多尺度、旋转不变性且对光照变化不受影响的特征向量,SIFT算法特征提取分为5个步骤[8-10]:
1) 生成尺度空间.生成尺度空间是为了描述图像的多尺度特征,二维图像的尺度空间为L(x, y, σ)=G(x, y, σ)*I(x, y),其中:G(x, y, σ)表示尺度可变的高斯函数,
实验中需要在图像二维空间以及高斯差分函数中提取相同的局部极值点,以确保得到的是稳定且与尺度无关的关键点.Lowe利用多尺度高斯差分核与图像的卷积,得到高斯差分尺度空间
| $D\left( {x,{\rm{ }}y,{\rm{ }}\sigma } \right) = \left( {G\left( {x,{\rm{ }}y,{\rm{ }}k\sigma } \right) - G\left( {x,{\rm{ }}y,{\rm{ }}\sigma } \right)} \right)*I\left( {x,{\rm{ }}y} \right) = L\left( {x,{\rm{ }}y,{\rm{ }}k\sigma } \right) - L\left( {x,{\rm{ }}y,{\rm{ }}\sigma } \right),$ |
其中:D(x, y, σ)为差分金字塔;k为常数因子.
2) 检测极值点.在DOG中检测极值点时,将待检测点与和它同尺度的8个邻域点,以及上下相邻尺度的2×9=18个,共26个领域点进行比较,以确保在尺度空间和二维图像空间都检测到极值点.如果一个点在DOG尺度空间本层及上下两层的26个领域内是最大值或最小值时,就认为该点是图像在该尺度下的一个候选点.
假设高斯金字塔每组有n层,则它构建的DOG金字塔每组层数应该是n-1,而DOG的搜索特征点的过程是从每组的第2层到倒数第2层,因此实际搜索的层数应该是n-3.
3) 精确定位极值点.确定候选点之后,利用尺度空间函数D(x, y, σ)的泰勒二次展开式,进行最小二乘拟合来确定图像关键点的精确位置和尺度,同时去除低对比度点和边缘点,以增强匹配稳定性.关键点处的拟合泰勒二次展开式为
| $\mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{X}} \right) = \mathit{\boldsymbol{D}} + \frac{{\partial {\mathit{\boldsymbol{D}}^{\rm{T}}}}}{{\partial \mathit{\boldsymbol{X}}}}\mathit{\boldsymbol{X}} + \frac{1}{2}{\mathit{\boldsymbol{X}}^{\rm{T}}}\frac{{{\partial ^2}\mathit{\boldsymbol{D}}}}{{{\partial ^2}\mathit{\boldsymbol{X}}}}\mathit{\boldsymbol{X}}.$ |
4) 确定关键点方向参数.利用边缘强度m(x, y)和边缘方向θ(x, y)求取.公式分别为:
| $\begin{array}{l} m\left( {x,{\rm{ }}y} \right) = \sqrt {{{\left( {L\left( {x + 1,{\rm{ }}y} \right) - L\left( {x - 1,{\rm{ }}y} \right)} \right)}^2} + {{\left( {L\left( {x,{\rm{ }}y + 1} \right) - L\left( {x,{\rm{ }}y - 1} \right)} \right)}^2}} ,\\ \theta \left( {x,{\rm{ }}y} \right) = {\rm{ta}}{{\rm{n}}^{ - 1}}\left( {L\left( {x + 1,{\rm{ }}y} \right) - L\left( {x - 1,{\rm{ }}y} \right)} \right)/\left( {L\left( {x,{\rm{ }}y + 1} \right) - L\left( {x,{\rm{ }}y - 1} \right)} \right). \end{array}$ |
为确定关键点的主方向,用直方图统计以关键点为中心的领域窗口内像素的梯度方向.直方图的峰值代表了关键点处领域梯度的主方向,即关键点处的主方向.在梯度直方图中,当存在另一个相当于主峰值80%能量的峰值时,则这个方向作为关键点处的辅方向,以增强匹配的鲁棒性.
5) 生成特征描述子.首先将坐标轴旋转到特征点的主方向,确保旋转不变性.以关键点为中心,取16×16的窗口,在每个4×4的小块上,计算8个方向的梯度方向直方图,绘制每个梯度方向的累加值,即可形成一个种子点.这样对于一个种子点会产生4×4×8共128维的虹膜特征向量,即特征描述子.
3.2 特征匹配为了在众多图像中识别出与当前图像匹配的图像,需要对当前图像和目标图像的特征点进行特征匹配.具体是使用欧式距离来表征两幅图像的相似性,即在待匹配的图像中找到与当前图像中某个特征点n1、欧式距离最近的特征点n2和次近的特征点n3,假设LO(ni, nj)表示两个特征点ni和nj之间的距离,若LO(n1, n2)/LO(n1, n3)的距离之比小于某个阈值,则认为n1和n2是一对匹配点,否则认为n1在待匹配图像中没有特征点与之匹配.
4 Harris角点检测算法Harris算子[11]用高斯函数无穷小位移向任何方向移动,灰度变化的定义为
| $E\left( {u,{\rm{ }}v} \right) = \sum\limits_{x,y} {w\left( {x,{\rm{ }}y} \right)} {\left[ {I\left( {x + u,{\rm{ }}y + u} \right) - I\left( {x,{\rm{ }}y} \right)} \right]^2} = \sum\limits_{x,y} {w\left( {x,{\rm{ }}y} \right)} {[{I_x}u + {I_y}v + O({u^2} + {v^2})]^2},$ |
变成矩阵的形式
| $\mathit{\boldsymbol{M}} = \sum\limits_{x,y} {w\left( {x,{\rm{ }}y} \right)} \left[ {\begin{array}{*{20}{c}} {I_x^2} & {{I_x}{I_y}}\\ {{I_x}{I_y}} & {I_y^2} \end{array}} \right] = w\left( {x,{\rm{ }}y} \right) \otimes \left[ {\begin{array}{*{20}{c}} {I_x^2} & {{I_x}{I_y}}\\ {{I_x}{I_y}} & {I_y^2} \end{array}} \right].$ |
灰度变化的公式可变为
Harris采用了一种新的角点判定方法.矩阵M的两个特征向量λ1和λ2与矩阵M的主曲率成正比. Harris分别利用λ1、λ2来表征最快和最慢的两个方向.若两个都很大就是角点,一个大一个小就是边缘点,两个都很小就是在变化缓慢的图像区域,如图 6所示.
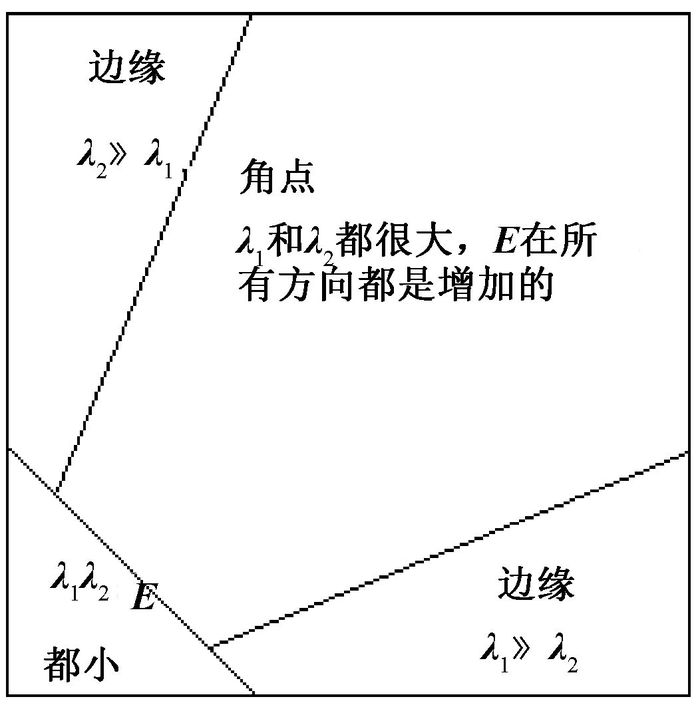
|
图 6 Harris角点判定方法 Figure 6 Determination method of Harris corner |
文中首先采用SIFT算法提取虹膜图像的特征点,由于提取的特征点有伪特征点和边缘点,因此本文提出了改进的SIFT算法.用Harris角点检测算法筛选出高对比度的特征点,进而提高匹配效率.
在改进的SIFT算法特征点匹配时,每一幅虹膜图像的SIFT特征点数量较多且均为128维,占用内存大,计算量庞大,因此本文采用街区距离[12]代替欧式距离进行特征匹配,从而降低了计算的复杂度,提高匹配的速度.
欧式距离进行特征匹配公式为:
街区距离进行特征匹配为:
根据上述公式可知,在欧式距离的一次计算中,需要128次减法运算,128次平方运算,127次加法运算和1次开平方运算;而街区距离的一次计算在运算量方面比欧式距离少了一次开平方运算.由于SIFT特征点数目庞大,所以减少一次开平方运算的方法也是有价值的.
6 实验结果本文在MATLAB R2014a环境下采用中科院自动化研究所提供的CASIA V1.0虹膜数据库图像(108组虹膜,每组虹膜有7幅图像,共756幅虹膜图像)作为实现算法的实验样本.对实验数据和实验结果分析发现,改进后的算法和原算法相比,对于特征点的筛选率和特征点的匹配正确率,均呈现了较大的提高.限于篇幅,本文使用3幅图像作为样本进行实验结果说明.
虹膜特征提取阶段,对定位后的图像分别采用原SIFT算法和使用Harris算子改进后的算法,对3幅样本图像进行特征点的提取,实验结果如表 1所示.每幅图像分别使用原SIFT算法提取的特征点和利用Harris角点检测算法提取的特征点,可以明显看出,Harris角点检测算法将睫毛上和边缘上的伪特征点进行筛选,特征点的数量明显下降,留下优质的特征点为下一步的匹配奠定了良好的基础.
|
|
表 1 SIFT算法特征点提取以及筛选后的特征点 Table 1 SIFT algorithm feature points extraction and the feature points of after filtering |
虹膜特征匹配阶段,分别对改进前的SIFT算法和改进后的SIFT算法利用街区距离进行匹配.在SIFT算法中Lowe根据实验确定的经验阈值为0.8,为对比分析两种算法的区别,本文也采用匹配阈值为0.8的情况下,使用不同算法分别对3幅样本所提取特征点个数、正确匹配数、匹配时间及匹配率进行对比.改进前和改进后的算法匹配结果分别如表 2、表 3所示.实验数据结果表明:在设定较为合适的匹配阈值(0.8) 后,改进后的算法相较于原算法,较大地提高了正确匹配率,提高了算法的运算效率,减少了误匹配率.
|
|
表 2 不同SIFT算法匹配结果 Table 2 Matching results of different SIFT algorithm |
|
|
表 3 不同SIFT算法实验结果 Table 3 Experimental results of different SIFT algorithm |
本文采用SIFT算法直接提取定位出的虹膜图像的纹理特征,进而利用Harris算子对提取到的特征点进行筛选,在特征匹配阶段,利用街区距离分别对原SIFT算法和改进后的SIFT算法提取到的虹膜特征向量进行相似度匹配.本文改进的算法没有改变特征点的维数,因此保留了原算法鲁棒性的同时提高了SIFT算法匹配的效率.与原算法相比,本文提出的算法具有广阔的应用场景,为实时性要求较高的应用场合提供了保障.
| [1] |
DAUGMAN J. How iris recognition works[J]. IEEE transactions on circuits and systems for video technology, 2004, 14(1): 21-30. DOI:10.1109/TCSVT.2003.818350 (  0) 0) |
| [2] |
BOLES W W. A security system based on human iris identification using wavelet transform[C]//IEEE 1998 International Conference on Knowledge-Based Intelligent Electronic Systems. New York, 1998, (2):533-541.
(  0) 0) |
| [3] |
WILDES R P, ASMUTH J C, GREEN G L, et al. A system for automated iris recognition[C]// Applications of Computer Vision, Proceedings of the Second IEEE Workshop on. Florida, 2002:121-128.
(  0) 0) |
| [4] |
曹国辉. 基于神经网络的虹膜识别分类器的设计[D]. 武汉: 武汉理工大学, 2006. http://d.wanfangdata.com.cn/Thesis/Y864382
(  0) 0) |
| [5] |
张震, 张英杰. 基于支持向量机与Hamming距离的虹膜识别方法[D]. 郑州: 郑州大学, 2015. http://d.wanfangdata.com.cn/Periodical/zzgydxxb201503006
(  0) 0) |
| [6] |
汤海林. 基于SIFT的图像特征提取算法研究[J]. 电脑开发与应用, 2013, 26(8): 54-56. (  0) 0) |
| [7] |
SUN S N, YANG S C, ZHAO L D. Noncooperative bovine iris recognition via SIFT[J]. Neurocomputing, 2013, 120(10): 310-317. (  0) 0) |
| [8] |
LOWE D. Distinctive image features from scale invariant key points[J]. International journal of computer vision, 2004, 60(60): 91-110. (  0) 0) |
| [9] |
万剑华, 孙姝娟, 曾喆. SIFT算法距离比阈值自适应改进研究[J]. 中国石油大学学报(自然科学版), 2013, 37(4): 71-75. (  0) 0) |
| [10] |
白廷柱, 侯喜报. 基于SIFT算子的图像匹配算法研究[J]. 北京理工大学学报, 2013, 33(6): 622-627. (  0) 0) |
| [11] |
林强. 一种改进的SIFT图像匹配算法[J]. 现代计算机(普遍版), 2015(2): 58-62. (  0) 0) |
| [12] |
王晓华, 傅卫平, 梁元月. 提高SIFT特征匹配效率的方法研究[J]. 机械科学与技术学报, 2009, 28(9): 1252-1255. (  0) 0) |
 2017, Vol. 49
2017, Vol. 49