在科学和工程领域中, 很多问题最终都可归结为大型线性方程组的求解, 文献[1]提出的基于Galerkin原理的GMRES(m)算法是公认的求解大型非对称线性方程组较为成功的方法之一, 同时也是快速多极边界元法中的求解器。
随着GMRES算法和相关知识被广泛学习, 很多学者也对该算法进行了优化和改进。一种方法是采用预处理技术[2-4]。刘晓明等[5]将GMRES方法应用于油藏数值模拟计算问题, 利用矩阵分块技术, 采用块拟消去法(PE)对系数矩阵进行了预处理。于春肖等[6]提出ILU预处理Householder-GMRES(m)算法, 通过降低系数矩阵的条件数达到加快收敛的目的。关朋燕等[7]将多项式预处理与加权GMRES(m)相结合, 构造出一种新的方法, 减少了计算量。于春肖等[8]通过改变重启动参数m的值提出VRP-HGMRES(m)算法, 该算法有效地避免了因重启动参数的选取不当而造成的问题。文献[9]将稀疏矩阵的小特征值对应的特征向量加入Krylov子空间。于春肖等[10]提出一种截断型IGMRES(m)新算法, 此算法是基于FMM的Krylov子空间投影类方法。郝雪景等[11]提出基于不完全正交的变参数IGMRES(m)算法。Walker[12]对GMRES算法进行改进, 提出一种基于Householder变换的GMRES(简称H-GMRES)算法。
本文将利用截断技术[13-14]给出一种不完全正交的变参数H-IGMRES(m)算法, 使计算量大大减少, 并结合数值算例分析该算法的高效性。
1 H-GMRES(m)算法在实际计算中, H-GMRES(m)算法构造Hessenberg矩阵元素和Krylov向量时都要用到较长的递推式, 从而导致消耗的计算时间很长, 迭代过程数值也不稳定。这种算法的具体步骤为:
1) 给定重启动参数m和误差上界ε>0, 取初始值x(0)∈Rn, 计算r(0)=b-Ax(0), β=‖r(0)‖2。
2) 计算P1=I-2ωωΤ, 其中:‖ω‖2=1;P1r(0)=βe1;v1=P1e1。
3) 对于j=1, 2, …, m,令cj=PΤAvj(当j=1时, 有P=P1成立), 然后计算
| $ {\mathit{\boldsymbol{P}}_{j + 1}} = \mathit{\boldsymbol{I}} - 2{\mathit{\boldsymbol{c}}_j}\mathit{\boldsymbol{c}}_j^{\rm{T}}/\left\| {{\mathit{\boldsymbol{c}}_j}} \right\|_2^2,\mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{P}}_2} \cdots {\mathit{\boldsymbol{P}}_{j + 1}}, $ |
| $ {\mathit{\boldsymbol{v}}_{j + 1}} = {\mathit{\boldsymbol{P}}_{j + 1}}{\mathit{\boldsymbol{P}}_j} \cdots {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{e}}_{j + 1}},{\mathit{\boldsymbol{h}}_j} = {\mathit{\boldsymbol{P}}_{j + 1}}{\mathit{\boldsymbol{c}}_{j}}。$ |
形成Hm和Vm, 从而变成求解最小二乘问题ym=arg min‖βe1-Hmy‖2,y∈Rm。得出原方程组的近似解x(m)=x(0)+zm=x(0)+Vmym。
4) 如果‖r(0)-Azm‖2 < ε,则x=x(m), 迭代停止;否则x(0)=x(m), m=m+1且转向1)再一次迭代, 直到满足给定的误差上界为止。
2 H-IGMRES(m)算法与收敛性分析 2.1 H-IGMRES(m)算法当m很大时, H-GMRES(m)算法需要计算和保存所有的{vi}i=1m, 这将需要很大的存储空间。当问题规模很大时, 有可能引起内存不足。基于H-GMRES(m)算法, 利用截断技术, 本文提出H-IGMRES(m)算法, 其基本思想是在采用Householder变换构造Krylov子空间的基向量时, 仅使用部分而非所有前面计算出的向量来构造新的递推式以计算后面的向量, 从而减少算法的计算量, 即仅对前面的至多k个向量vj0, …, vj, j0=max{1, j-k-1}进行正交的Householder变换, 其中k < m, 定义截断指标q0=j0=max{1, j-k-1}, 截断比为(m-q0)/m。具体步骤如下:
1) 初始化:给定重启动参数m和误差上界ε>0, 设置截断指标q0, 取初始值x(0)∈Rn, 计算
| $ {\mathit{\boldsymbol{r}}^{\left( 0 \right)}} = \mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}^{\left( 0 \right)}},\beta = {\left\| {{\mathit{\boldsymbol{r}}^{\left( 0 \right)}}} \right\|_2}。$ |
2) 计算P1=I-2ωωΤ, 其中‖ω‖2=1;P1r(0)=βe1;v1=P1e1。
3) 对于j=1, 2, …, m有不完全正交化, 令cj=PΤAvj(当j=1时, 有P=P1成立), 然后计算
| $ {\mathit{\boldsymbol{P}}_{j + 1}} = \mathit{\boldsymbol{I}} - 2{\mathit{\boldsymbol{c}}_j}\mathit{\boldsymbol{c}}_j^{\rm{T}}/\left\| {{\mathit{\boldsymbol{c}}_j}} \right\|_2^2,\mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{P}}_{{q_0}}} \cdots {\mathit{\boldsymbol{P}}_{j + 1}}, $ |
| $ {\mathit{\boldsymbol{v}}_{j + 1}} = \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{e}}_{j + 1}},{\mathit{\boldsymbol{h}}_j} = {\mathit{\boldsymbol{P}}_{j + 1}}{\mathit{\boldsymbol{c}}_j}。$ |
更新Vj+1与Hj,Vj+1=(Vj, vj+1),Hj=(Hj-1, hj)(j+1)×j。
Hj为(j+1)×j的带状上Hessenberg矩阵,其非零元素由上式生成。当j=1时第一列省略, 并且有
| $ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{V}}_m} = {\mathit{\boldsymbol{V}}_{m + 1}}{{\mathit{\boldsymbol{\bar H}}}_m}。$ |
求解最小二乘问题
| $ {\mathit{\boldsymbol{y}}_m} = \arg \min{\left\| {\beta {\mathit{\boldsymbol{e}}_1} - {{\mathit{\boldsymbol{\bar H}}}_m}\mathit{\boldsymbol{y}}} \right\|_2},\mathit{\boldsymbol{y}} \in {{\bf{R}}^m}, $ |
得出原方程组的近似解x(m)=x(0)+zm=x(0)+Vmym。
4) 如果‖r(0)-Azm‖2 < ε,则x=x(m), 迭代停止;否则x(0)=x(m), m=m+1且转向1)再一次迭代, 直到满足给定的误差上界为止。
2.2 收敛性分析为研究这种截断型H-IGMRES(m)算法的收敛形态, 这里将H-IGMRES(m)算法和H-GMRES(m)算法结合起来, 以建立H-IGMRES(m)算法的收敛性理论。
定义Vm+1=(v1, v2, …, vm+1), 可以证明, 如果H-IGMRES(m)算法在m步中断且Vm+1列满秩, 则得到的数值解为准确解x*。另外, 当q0=1时, H-IGMRES(m)算法与H-GMRES(m)算法相同。为讨论方便, 选取Km=span{r(0), Ar(0), …, Am-1r(0)}, 将H-IGMRES(m)算法进行m步迭代后的数值解表示为x(m)(HI), 残余向量表示为r(m)(HI); 将H-GMRES(m)算法进行m步迭代后的数值解表示为x(m)(H), 残余向量表示为r(m)(H)。
定理1 假设Vm+1列满秩,则H-IGMRES(m)算法和H-GMRES(m)算法在Km上的残值范数满足
| $ \left\| {{\mathit{\boldsymbol{r}}^{\left( m \right)}}\left( {\mathit{\boldsymbol{HI}}} \right)} \right\| \le S\left( {{\mathit{\boldsymbol{V}}_{m + 1}}} \right)\left\| {{\mathit{\boldsymbol{r}}^{\left( m \right)}}\left( \mathit{\boldsymbol{H}} \right)} \right\|。$ | (1) |
其中Vm+1由不完全正交化过程生成, S(Vm+1)=‖Vm+1‖‖Vm+1+‖, Vm+1+是Vm+1的广义逆矩阵。如果H-IGMRES(m)算法在m步中断, 即hm+1, m=0, 则x(m)(HI)=x*。
证明 由r(0)=βVm+1e1和AVm=Vm+1Hm可知, 对应于x(m)(HI)的残值为
| $ {\mathit{\boldsymbol{r}}^{\left( m \right)}}\left( {\mathit{\boldsymbol{HI}}} \right) = \mathit{\boldsymbol{b}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}^{\left( m \right)}}\left( {\mathit{\boldsymbol{HI}}} \right) = {\mathit{\boldsymbol{V}}_{m + 1}}\left( {\beta {\mathit{\boldsymbol{e}}_1} - {{\mathit{\boldsymbol{\bar H}}}_m}{\mathit{\boldsymbol{y}}_m}} \right)。$ |
因此
| $ \left\| {{\mathit{\boldsymbol{r}}^{\left( m \right)}}\left( {\mathit{\boldsymbol{HI}}} \right)} \right\| = \left\| {{\mathit{\boldsymbol{V}}_{m + 1}}\left( {\beta {\mathit{\boldsymbol{e}}_1} - {{\mathit{\boldsymbol{\bar H}}}_m}{\mathit{\boldsymbol{y}}_m}} \right)} \right\|。$ | (2) |
由r(0)=βVm+1e1, 可得Vm+1+r(0)=βe1, 再由AVm=Vm+1Hm可得Hm=Vm+1+AVm。
因此, 式(2)变成
| $ \left\| {{\mathit{\boldsymbol{r}}^{\left( m \right)}}\left( {\mathit{\boldsymbol{HI}}} \right)} \right\| = \left\| {{\mathit{\boldsymbol{V}}_{m + 1}}\left( {{\mathit{\boldsymbol{V}}_{m + 1}}^ + {\mathit{\boldsymbol{r}}^{\left( 0 \right)}} - {\mathit{\boldsymbol{V}}_{m + 1}}^ + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{V}}_m}{\mathit{\boldsymbol{y}}_m}} \right)} \right\|。$ |
式
| $ \mathop {\min }\limits_{{y_m} \in {{\bf{R}}^m}} \left\| {{\mathit{\boldsymbol{V}}_{m + 1}}^ + {\mathit{\boldsymbol{r}}^{\left( 0 \right)}} - {\mathit{\boldsymbol{V}}_{m + 1}}^ + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{V}}_m}{\mathit{\boldsymbol{y}}_m}} \right\| = \mathop {\min }\limits_{{z_m} \in {K_m}} \left\| {{\mathit{\boldsymbol{V}}_{m + 1}}^ + {\mathit{\boldsymbol{r}}^{\left( 0 \right)}} - {\mathit{\boldsymbol{V}}_{m + 1}}^ + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{z}}_m}} \right\|。$ |
因此可得
| $ \begin{array}{l} \left\| {{\mathit{\boldsymbol{r}}^{\left( m \right)}}\left( {\mathit{\boldsymbol{HI}}} \right)} \right\| \le \left\| {{\mathit{\boldsymbol{V}}_{m + 1}}} \right\|\left\| {\left( {{\mathit{\boldsymbol{V}}_{m + 1}}^ + {\mathit{\boldsymbol{r}}^{\left( 0 \right)}} - {\mathit{\boldsymbol{V}}_{m + 1}}^ + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{V}}_m}{\mathit{\boldsymbol{y}}_m}} \right)} \right\| = \\ \left\| {{\mathit{\boldsymbol{V}}_{m + 1}}} \right\|\mathop {\min }\limits_{{z_m} \in {K_m}} \left\| {{\mathit{\boldsymbol{V}}_{m + 1}}^ + {\mathit{\boldsymbol{r}}^{\left( 0 \right)}} - {\mathit{\boldsymbol{V}}_{m + 1}}^ + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{z}}_m}} \right\| \le \\ \left\| {{\mathit{\boldsymbol{V}}_{m + 1}}} \right\|\left\| {{\mathit{\boldsymbol{V}}_{m + 1}}^ + } \right\|\mathop {\min }\limits_{{z_m} \in {K_m}} \left\| {{\mathit{\boldsymbol{r}}^{\left( 0 \right)}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{z}}_m}} \right\| = \\ S\left( {{\mathit{\boldsymbol{V}}_{m + 1}}} \right)\mathop {\min }\limits_{{z_m} \in {K_m}} \left\| {{\mathit{\boldsymbol{r}}^{\left( 0 \right)}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{z}}_m}} \right\| = S\left( {{\mathit{\boldsymbol{V}}_{m + 1}}} \right)\left\| {{\mathit{\boldsymbol{r}}^{\left( m \right)}}\left( \mathit{\boldsymbol{H}} \right)} \right\|, \end{array} $ |
所以式(1)成立。
如果hm+1, m=0, 则AVm=Vm+1Hm变为AVm=VmHm, 其中Hm是去掉Hm最后一行的m×m带状上Hessenberg矩阵, Vm的列张成A的一个不变子空间。所以, Hm的特征值均为A的特征值, 从而Hm非奇异。现在‖r(m)(HI)‖=‖r(0)-AVmym‖=‖r(0)-VmHmym‖=‖Vm(βe1-Hmym)‖, 而当ym=βHm-1e1时, 有
例1 考虑两点边值问题
此问题的精确解为
| $ Ay = b,A \in {{\bf{R}}^{{{\left( {n - 1} \right)}^2} \times {{\left( {n - 1} \right)}^2}}},y,b \in {{\bf{R}}^{{{\left( {n - 1} \right)}^2}}}。$ |
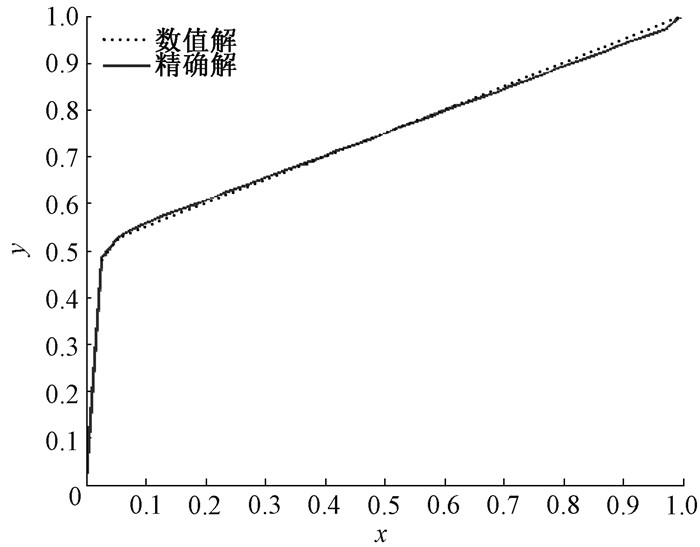
如果选取p=0.01, q=0.5, n=40, 初始向量为y(0)=(0, …, 0)Τ, 误差上界为t=1e-6, 当m=10时, 取截断指标为9, 用H-IGMRES(m)算法求解该线性方程组, 将得到的数值解与精确解进行比较, 如图 1所示。从图 1可看出, 数值解和精确解完全吻合, 证明此算法的可行性。
|
图 1 精确解与数值解的比较 Fig. 1 Comparison of exact solution and numerical solution |
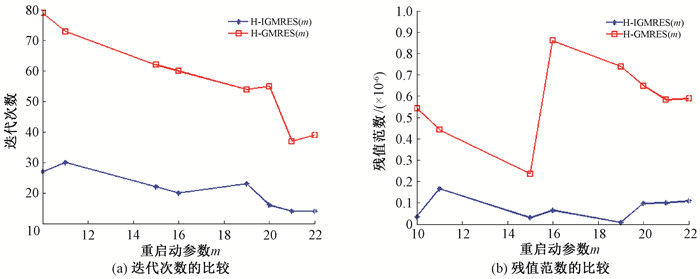
下面选取n=100, 分别用H-IGMRES(m)算法和H-GMRES(m)算法求解这个线性方程组。当重启动参数不同时, 两种算法所需的迭代次数和得到的残值范数如图 2所示, 两种算法所需的运行时间见表 1。从图 2和表 1可看出, 重启动参数不同时, H-IGMRES(m)算法与H-GMRES(m)算法相比, 前者迭代次数和运行时间较少, 说明新算法提高了计算效率, 并且具有更高的计算精度。
|
图 2 两种算法计算效率与计算精度的比较 Fig. 2 Comparison of computational efficiency and accuracy between two algorithms |
|
|
表 1 当重启动参数不同时, 两种算法运行时间比较(m=10) Tab. 1 Comparison of running time under different meshes for the two algorithms(m=10) |
例2 考虑如下二维Possion方程, 其中Ω{(x, y) 0≤x≤1, 0≤y≤1},u(x, y)为温度分布函数。
| $ \left\{ \begin{array}{l} - \left( {{u_{xx}} + {u_{yy}}} \right) = 2{{\rm{ \mathsf{ π} }}^2}\sin {\rm{ \mathsf{ π} }}x\sin {\rm{ \mathsf{ π} }}y,\left( {x,y} \right) \in \mathit{\Omega }\\ u\left( {x,y} \right) = 0,\left( {x,y} \right) \in \partial \mathit{\Omega } \end{array} \right.。$ |
令f(x, y)=2π2sin πxsin πy, 将求解区域沿x方向和y方向进行等分, 由五点差分法可得Au=b, A∈Rn2×n2, u, b∈Rn2×1。
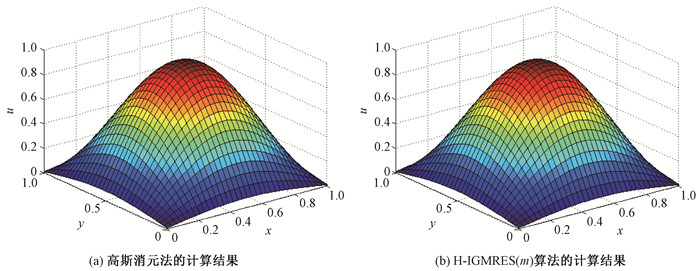
当n=35时, 选取重启动参数m=20及截断指标q0=9, 分别用高斯消元法和H-IGMRES(m)算法求解线性方程组, 其结果分别如图 3(a)和3(b)所示。
|
图 3 温度分布 Fig. 3 Temperature distribution |
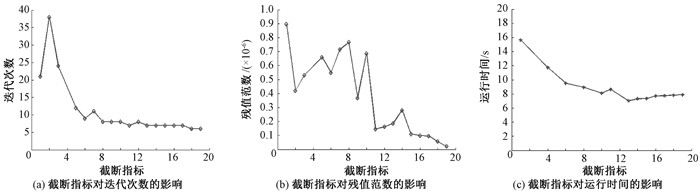
由图 3可以看出, 两种算法的计算结果完全一致, 这表明H-IGMRES(m)算法是正确的。截断指标可以在1~19中取值, 不同的截断指标对计算速率、计算精度、运行时间的影响如图 4所示。
|
图 4 截断指标对计算速率、计算精度、运行时间的影响 Fig. 4 Effect of truncation index on computional rate, computional accuracy, operation time |
由图 4可看出, 迭代次数和残值范数随截断指标的增大呈下降趋势, 运行时间也在突降之后逐渐趋于平稳, 说明截断技术在保证计算精度的前提下提高了计算效率。当m=10时, 随着计算规模n的不断增大, 当残值范数满足给定的误差上界时, H-IGMRES(m)算法总的运行时间要比H-GMRES(m)算法少很多, 进一步说明了H-IGMRES(m)算法的优越性, 见表 2。
|
|
表 2 不同网格下两种算法运行时间比较(m=10) Tab. 2 Comparison of running time under different meshes for the two algorithms(m=10) |
1) 提出了H-IGMRES(m)算法, 对算法的收敛性进行了理论分析。
2) 数值算例表明H-IGMRES(m)算法的计算结果和精确解吻合, 说明该算法的有效性。
3) 分析了截断指标的选取对算法的计算精度和效率的影响, 证明了H-IGMRES(m)算法的计算效率和精度都高于H-GMRES(m)算法。
| [1] |
SAAD Y, SCHULTZ M H. A generalized minimum residual algorithm for solving nonsymmetric linear systems[J]. SIAM journal on scientific and statistical computing, 1986, 7(3): 856-869. DOI:10.1137/0907058 (  0) 0) |
| [2] |
陈泽军, 肖宏. 预条件GMRES(m)法迭代求解大规模边界元弹性问题[J]. 固体力学学报, 2006, 27(S1): 50-55. CHEN Z J, XIAO H. Iterative solution of large-scale BEM elasticity problems using preconditioned GMRES(m) technique[J]. Chinese journal of solid mechanics, 2006, 27(S1): 50-55. (  0) 0) |
| [3] |
BAGLAMA J, CALVETTI D, GOLUB G H, et al. Adaptively preconditioned GMRES algorithms[J]. SIAM journal on scientific computing, 1998, 20(1): 243-269. (  0) 0) |
| [4] |
段文洋, 刁峰, 陈纪康. 预条件GMRES(m)算法在大型浮体水动力边界元分析中的应用[J]. 哈尔滨工程大学学报, 2013(11): 1363-1368. DUAN W Y, DIAO F, CHEN J K. Application of preconditioned and restarted GMRES(m) to the boundary element analysis of large floating structures[J]. Journal of Harbin engineering university, 2013(11): 1363-1368. (  0) 0) |
| [5] |
刘晓明, 卢志明, 刘宇陆. Krylov子空间投影法及其在油藏数值模拟中的应用[J]. 应用数学和力学, 2000, 21(6): 551-560. LIU X M, LU Z M, LIU Y L. Krylov subspace projection method and its application on oil reservoir simulation[J]. Applied mathematics and mechanics, 2000, 21(6): 551-560. DOI:10.3321/j.issn:1000-0887.2000.06.001 (  0) 0) |
| [6] |
YU C X, SONG H, YUAN R H. ILU pretreatment householder-GMRES (m) algorithm[J]. Journal of information and computational science, 2013, 10(13): 4287-4294. DOI:10.12733/jics20102146 (  0) 0) |
| [7] |
关朋燕, 李春光, 景何仿. 基于加权GMRES的多项式预处理广义极小残差法[J]. 工程数学学报, 2014, 31(5): 697-706. GUAN P Y, LI C G, JING H F. A weighted GMRES method based on polynomial preconditioning generalized minimal residual method[J]. Chinese journal of engineering mathematics, 2014, 31(5): 697-706. DOI:10.3969/j.issn.1005-3085.2014.05.007 (  0) 0) |
| [8] |
YU Chunxiao, REN Cuihuan, BAI Xueting. VRP-GMRES(m) iteration algorithm for fast multipole boundary element method[J]. Mathematical and computational applications, 2016, 21(4): 49. DOI:10.3390/mca21040049 (  0) 0) |
| [9] |
MORGAN R B. A restarted GMRES method augmented with eigenvectors[J]. SIAM journal on matrix analysis and applications, 1995, 16(4): 1154-1171. DOI:10.1137/S0895479893253975 (  0) 0) |
| [10] |
于春肖, 杨爱民, 弓小影. 基于FMM的Krylov子空间IGMRES(m)新算法及其应用[J]. 河北大学学报(自然科学版), 2006, 26(5): 452-455. YU C X, YANG A M, GONG X Y. New IGMRES(m) algorithm in Krylov subspace based on the FMM and its application[J]. Journal of Hebei university(natural science edition), 2006, 26(5): 452-455. DOI:10.3969/j.issn.1000-1565.2006.05.002 (  0) 0) |
| [11] |
郝雪景, 于春肖, 任翠环. 基于不完全正交的VRP-IGMRES(m)算法[J]. 河北大学学报(自然科学版), 2018, 38(5): 460-465. HAO X J, YU C X, REN C H. VRP-IGMRES(m) algorithm based on incomplete orthogonalization[J]. Journal of Hebei university(natural science edition), 2018, 38(5): 460-465. DOI:10.3969/j.issn.1000-1565.2018.05.003 (  0) 0) |
| [12] |
WALKER H F. Implementation of the GMRES method using householder transformations[J]. SIAM journal on scientific and statistical computing, 1988, 9(1): 152-163. DOI:10.1137/0909010 (  0) 0) |
| [13] |
ZHONG X J. IOM(q):incomplete orthogomalization method for large unsymmetric linear systems[J]. Numerical linear algebra with applications, 2015, 3(6): 491-512. (  0) 0) |
| [14] |
贾仲孝. 解非对称线性方程组的不完全广义最小残量法[J]. 中国科学:A辑, 1998, 28(8): 694-702. JIA Z X. Incomplete generalized minimum residual method for solving asymmetric linear equations[J]. Chinese science: series A, 1998, 28(8): 694-702. (  0) 0) |
 2020, Vol. 52
2020, Vol. 52


