2. 长安大学 理学院 陕西 西安 710061
2. School of Science, Chang′an University, Xi′an 710061, China
人工蜂群算法(artificial bee colony,ABC)是模仿蜜蜂群体采蜜行为提出来的一种启发式智能优化算法,与遗传算法(genetic algorithm,GA)[1]、差分进化算法(differential evolution,DE)[2]、蚁群算法(ant colony optimization,ACO)[3]和粒子群算法(particle swarm optimization,PSO)[4]相比,由于ABC算法具有参数少、精度高和结构简单易实现等优点,近几年来受到广泛的关注,并被应用到数据挖掘[5]、生产调度[6]和信息处理[7]等领域。
与其他优化算法相似,ABC算法在解决复杂优化函数时,存在收敛速度慢、算法后期种群多样性下降及易陷入局部最优解等缺点。许多学者对其进行改进,主要在提高算法的收敛速度、增加种群的多样性以及改进算法的寻优机制等方面尝试。Gao等提出了基于差分进化算子的改进人工蜂群算法[8];Zhu等受到粒子群算法的影响,利用最优解指导雇佣蜂的局部搜索[9];魏锋涛等引入量子行为模拟蜂群求解过程[10];赵玉霞等受到猫群思想搜索过程启发,对较优解与较差解分别执行搜寻与跟踪模式[11]。
以上研究主要改进了搜索公式,提升了算法的寻优效率。但仍存在不足之处:首先,在初始化阶段中随机产生初始种群,其随机性导致种群的多样性不足,不利于算法求得潜在最优解。其次,雇佣蜂搜索过程中仅利用先前个体的信息产生候选解, 这种机制利于勘探不利于开发。最后,算法后期种群多样性下降,导致算法收敛速度慢。为解决以上问题,本文在初始化阶段利用反向学习策略,根据种群的适应度值贪婪选择较优的初始个体,扩大种群的多样性,提高解的质量,加强算法跳出局部最优解的能力。同时,本文将雇佣蜂搜索过程与差分进化算法融合,并加入自适应策略平衡算法的勘探与开发能力,加快人工蜂群算法的收敛速度。最后,在侦查蜂阶段中引入混沌序列,增加种群的多样性。
1 改进的人工蜂群算法 1.1 基于反向学习策略的初始化阶段Tizhoosh提出反向学习策略(opposition-based learning,OBL)[12],并将其应用到神经网络及强化学习中,主要思想是在取值区域内同时考虑当前个体和与它方向相反的个体,质量更优的个体进入下一代。Rahnamayan等从数学的角度证明了与随机产生候选解的方式相比[13],反向学习策略不但可以提高种群的多样性,还可以提高解的质量,在一定程度上避免算法陷入局部最优。基于反向学习策略的反向初始种群的公式为
| $ x_{ij}^{{\rm{OBL}}} = k\left( {{x_{i\max }} - {x_{i\min }}} \right) - {x_{ij}}, $ | (1) |
式中:xijOBL表示根据反向学习生成的反向初始解;k是[0, 1]均匀分布的随机数;ximin和ximax分别表示解的上下界。
1.2 融合差分进化思想的自适应搜索阶段Gao等受到DE算法的启发[8],基于差分进化算子与雇佣蜂搜索阶段的性质,提出了ABC/best/1算法,本文算法在ABC/best/1算法的基础上加入自适应策略,平衡算法的勘探与开发能力,以加快算法的收敛速度,
| $ {v_{ij}} = a\left( t \right){x_{j{\rm{best}}}} + \left( {1 - a\left( t \right)} \right)R\left( {{x_{ij}} - {x_{kj}}} \right), $ | (2) |
| $ a\left( t \right) = \frac{{iter}}{{Maxcycle}}, $ | (3) |
式(2)中:a(t)表示自适应参数;xjbest表示当前种群中的最优解;k∈{1, 2, …,SN},j∈{1, 2, …,D},k和j都是随机选取的,且k≠i。式(3)中:iter表示当前迭代次数;Maxcycle表示最大的迭代次数。算法初期阶段应侧重于勘探能力,此时自适应参数取较小值;随着迭代次数的增加,算法后期阶段应侧重于开发能力,此时自适应参数取较大值。
1.3 基于混沌序列的侦查蜂阶段文献[11]指出,算法后期食物源的位置相似度高,导致位置更新速度慢;算法后期的多样性下降,导致搜索能力下降。混沌[14]是一种非线性现象,具有非周期性、遍历性、随机性等特点,即混沌序列在取值区域内不重复地遍历所有状态。本文算法在侦查蜂阶段中引入Logistic混沌序列,增加种群的多样性,加快算法的收敛速度。Logistic混沌序列的主要思想为
| $ {C_{i + 1}} = \mu \times {C_i} \times \left( {1 - {C_i}} \right), $ | (4) |
式中:μ为控制参数,当μ=4时,公式(4)处于完全混沌状态;Ci表示第i次的混沌映射变量,Ci是(0, 1)上均匀分布的随机数且Ci≠0.25, 0.5, 0.75, i=0, 1,…,M,为混沌序列的长度;初始混沌变量C0=0.32。
基于Logistic混沌序列侦查蜂搜索公式为
| $ {x_{ij}} = {x_{i\min }} + {C_j}\left( {{x_{i\max }} - {x_{i\min }}} \right)。$ | (5) |
综上所述,本文提出的融合差分进化思想的自适应ABC算法主要步骤如下。
Step1在D维空间中生成SN个初始解, 根据初始种群与反向种群的适应度值排序,贪婪选择SN个个体作为初始种群;
Step2雇佣蜂在初始位置的附近利用搜索公式(2)进行局部邻域搜索,贪婪选择适应度值较优的食物源;
Step3全部的雇佣蜂完成一次局部搜索后,观察蜂根据雇佣蜂提供的适应度值,按照概率Pi选择食物源,并在该食物源附近进行邻域搜索,寻找新的食物源,贪婪选择较优的食物源;
Step4如果食物源的收益率没有通过预先确定的循环次数(limit)得到改善时,该处食物源被放弃,与之对应的雇佣蜂转化为侦察蜂。侦察蜂利用公式(5)产生新解。
Setp5若迭代次数小于最大迭代次数,转至Step2;否则,输出最优解,算法结束。
2 仿真实验及结果分析为测试本文算法的性能, 选用表 1给出的基准函数[8]进行测试。其中:f1~f3为单峰函数,用于检验算法收敛速度和精度;f4~f8为多峰函数,其局部最优解的个数会随着问题维数的增加呈指数增长,用于检验算法的整体寻优能力和算法跳脱局部最优值的能力。针对表 1所列的8个函数,选取ABC算法、PSO算法、DE算法、EABC算法、ABC/best/1算法与本文算法分别在维数为50和100情况下独立运行50次,统计各算法的最优值、最差值、平均值和标准差,实验结果如表 2~5所示。平均值反映了算法的求解精度,标准差反映了算法的稳定性。
|
|
表 1 测试函数表达式、搜索空间和理论最优值 Tab. 1 Test function expressions, search spaces, and theoretical optimal values |
|
|
表 2 各算法在50维情况下对单峰函数测试的实验结果 Tab. 2 Experimental results of unimodal functions tested by each algorithm in 50 dimensions |
|
|
表 3 各算法在100维情况下对单峰函数测试的实验结果 Tab. 3 Experimental results of unimodal functions tested by each algorithm in 100 dimensions |
|
|
表 4 各算法在50维情况下对多峰函数测试的实验结果 Tab. 4 Experimental results of multi-modal functions tested by each algorithm in 50 dimensions |
|
|
表 5 各算法在100维情况下对多峰函数测试的实验结果 Tab. 5 Experimental results of multi-modal functions tested by each algorithm in 100 dimensions |
单峰函数实验结果(表 2)表明,ABC算法的稳定性差,收敛精度不高。实验结果可以看出,本文算法的最优值、最差值、平均值和标准差的精度与另外5种算法的精度相比都有明显提高。因此,说明在收敛速度和精度方面,本文算法优于其他算法,可以有效提高算法的局部搜索能力。多峰函数实验结果(表 4)表明,ABC算法易陷入局部最优值,整体寻优能力差。f4和f8函数的实验结果显示,本文算法的最优值和最差值的精度与其他5种算法相比都有提高;f5、f6和f7 3个函数的实验结果显示,本文算法的最优值、最差值与另外5种算法相比都有明显提高。因此说明,算法在整体寻优能力及跳脱局部最优解方面,本文算法整体寻优能力较高,易于跳出局部最优解。
2.2 不同维数相同算法的实验结果分析算法分别在50维和100维情况下,分别分析单峰函数实验结果(表 2和表 3)以及多峰函数实验结果(表 4和表 5)。数据表明:当维度是100时,f1、f2、f3、f5、f6和f7 6个函数的本文算法的寻优指标值优于另外5种算法;当函数维数降到50维时,本文算法的优势更为明显。
2.3 算法的性能测试为了更直观地反映算法的性能, 针对表 1所列的8个函数,分别采用ABC算法、DE算法、PSO算法、EABC算法、ABC/best/1算法与本文算法进行测试。图 1展示了维数为50时,6种算法对测试函数的收敛曲线(为便于发现曲线间的差距,将各函数的适应度值取对数)。
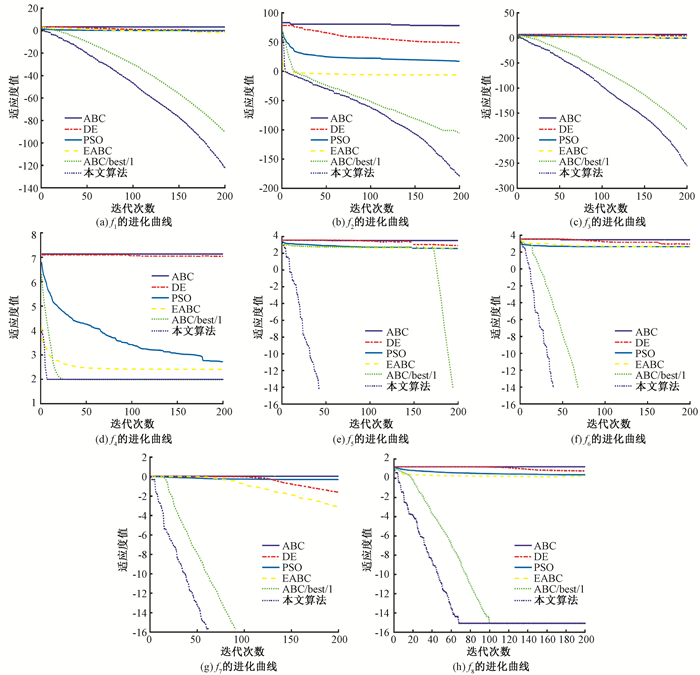
|
图 1 基准函数迭代曲线 Fig. 1 The evolution curve of benchmark functions |
根据图 1(a)~(c)的单峰函数进化曲线可以得出,在收敛速度和求解精度方面,本文算法明显优于另外5种算法。故本文算法大幅度加快了算法的收敛速度,提高了求解精度。图 1(d)为Rosenbrock函数的收敛曲线,该函数是一个病态的螺旋型函数,算法的初期阶段侧重于勘探能力,导致算法陷入局部最优解。随着迭代次数的增加,算法后期阶段侧重于开发能力,最优解的质量提高,对局部搜索行为指导作用明显。根据图 1(e)~(g)的函数进化曲线可以得出,本文算法在收敛速度、精度和全局优化能力方面明显优于其他5种算法,本文算法收敛速度快且易于跳出局部最优解。图 1(h)的函数进化曲线可以得出,在跳脱局部最优解方面,本文算法与其他5种算法相比都有提高。
| [1] |
TANG K S, MAN K F, KWONG S, et al. Genetic algorithms and their applications[J]. IEEE signal processing magazine, 1996, 13(6): 22-37. DOI:10.1109/79.543973 (  0) 0) |
| [2] |
STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 (  0) 0) |
| [3] |
DORIGO M, BLUM C. Ant colony optimization theory: a survey[J]. Theoretical computer science, 2005, 344(2/3): 243-278. (  0) 0) |
| [4] |
WANG Y C, LV J, ZHU L, et al. Crystal structure prediction via particle swarm optimization[J]. Physics, 2010, 82(9): 7174-7182. (  0) 0) |
| [5] |
梁显丽. 基于人工蜂群优化的多段支持度数据挖掘仿真[J]. 计算机仿真, 2019, 36(7): 273-276. LIANG X L. Multi-segment support data mining simulation based on artificial bee colony optimization[J]. Computer simulation, 2019, 36(7): 273-276. DOI:10.3969/j.issn.1006-9348.2019.07.058 (  0) 0) |
| [6] |
刘倩雯. 人工蜂群算法及其在调度问题中的应用研究[D]. 北京: 北京交通大学, 2014. LIU Q W. Research on artificial bee colony and its application in scheduling problems[D]. Beijing: Beijing Jiaotong University, 2014. (  0) 0) |
| [7] |
刘蓓蕾. 人工蜂群算法理论及其在信息处理中的应用研究[D]. 济南: 山东大学, 2016. LIU B L. Research on artificial bee colony algorithm theories and its application in information processing[D]. Jinan: Shandong University, 2016. (  0) 0) |
| [8] |
GAO W F, LIU S Y, HUANG L L. A global best artificial bee colony algorithm for global optimization[J]. Journal of computational and applied mathematics, 2012, 236(11): 2741-2753. DOI:10.1016/j.cam.2012.01.013 (  0) 0) |
| [9] |
ZHU G P, KWONG S. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied mathematics and computation, 2010, 217(7): 3166-3173. DOI:10.1016/j.amc.2010.08.049 (  0) 0) |
| [10] |
魏锋涛, 岳明娟, 郑建明. 基于改进邻域搜索策略的人工蜂群算法[J]. 控制与决策, 2019, 34(5): 965-972. WEI F T, YUE M J, ZHENG J M. Artificial bee colony algorithm based on improved neighborhood search strategy[J]. Control and decision, 2019, 34(5): 965-972. (  0) 0) |
| [11] |
赵玉霞, 徐晓钟, 黄维, 等. 基于猫群思想的混合人工蜂群算法[J]. 计算机技术与发展, 2019, 29(1): 90-96. ZHAO Y X, XU X Z, HUANG W, et al. Hybrid artificial bee colony algorithm based on thought of cat swarm[J]. Computer technology and development, 2019, 29(1): 90-96. (  0) 0) |
| [12] |
TIZHOOSH H R. Opposition-based learning: a new scheme for machine intelligence[C]//Proceedings of 2005 International Conference on Computational Intelligence for Modelling, Control and Automation. New York: IEEE Press, 2005: 695-701.
(  0) 0) |
| [13] |
RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition versus randomness in soft computing techniques[J]. Applied soft computing, 2008, 8(2): 906-918. (  0) 0) |
| [14] |
吴彤. 非线性动力学混沌理论方法及其意义[J]. 清华大学学报(哲学社会科学版), 2000, 15(3): 72-79. WU T. Nonlinear dynamic chaos theory method and its significance[J]. Journal of tsinghua university (philosophy and social sciences), 2000, 15(3): 72-79. (  0) 0) |
 2021, Vol. 53
2021, Vol. 53


