2. 高端海洋工程装备智能技术烟台市重点实验室 山东 烟台 264010
2. Yantai Key Laboratory of High-end Ocean Engineering Equipment and Intelligent Technology, Yantai 264005, China
水平集方法(level set method,LSM)是一种用于界面追踪和形状建模的数值技术。水平集方法的优点是可以在笛卡尔网格(Cartesian grid)上基于欧拉法(Eulerian approach)直接对演化中的曲线、曲面进行描述和数值计算, 不必对曲线、曲面进行参数化[1-2]。水平集方法的另一个优点是可以方便地追踪物体的拓扑结构的改变。在水平集方法应用中,为了在控制算法时间复杂度的同时保证轮廓的分辨率和水平集方程的求解精度,通常在算法中引入自适应网格[3-4]。
自适应网格方法(adaptive mesh refinement,AMR)是求解偏微分方程的工具。AMR的核心思想是:在迭代过程中,当某些区域变化剧烈(例如大变形、激波面、触间断面和滑移面等)时,该区域网格自动实现分级细化。因为AMR网格生成过程简单快速、自动化程度高、易于实现,在众多领域被广泛应用[5-6]。
但是采用AMR的水平集方法在实现过程中仍存在难点,由于AMR是一种分级细化的不均匀网格,在不同细化级别之间的节点(T节点)处会出现邻居节点集合不完整的情况,影响偏微分方程的近似求解。为了解决这一问题,近几年AMR相关研究中提出了最长边二分法[7-8]、最新顶点二分法[9-10]和red-green细化[11-13]等方法。使用最长二分法细化后不能保证子网格的形状规律性。尽管在文献[14-15]中证明了二维三角网格经过最长边二分法后得到的子网格的形状规律性,但在三维中仍是一个不确定问题。后两种则可以保持初始网格中某一元素的所有子代的形状规律性,相较于red-green细化, 最新顶点二分法属于复杂度较高的网格嵌套细化。事实上,red-green细化是对带有T节点的1-irregular网格常规细化的改进,其目的是实现细化网格的一致性。该细化规则首先在文献[11-12]提出,并在文献[16-18]中成功地扩展到高维的单纯网格。
水平集方程的求解是一个多次迭代求解的过程。引入AMR的水平集方法在结束每个时间步的计算后,需要重新确定细化和非细化网格,如果每次都进行网格的全局遍历会增加复杂度。针对这一问题,文献[19]提出了一种快速判断方法,即将遍历区域缩小到每个时间步计算所得曲面的临近网格,有效地减少了界面演化时的计算工作量。文献[20]开发了一种定位水平集,不需要在空间域中显式地找到界面位置的快速方法。该方法解决了如何将只在界面上给出的量扩展到界面邻域的重要问题。文献[21]将窄带法和快速行进近似法(the fast marching approximations)相结合,提出了一种用于研究生长过程中界面演化的算法,在重要的物理边界上建立了一个最高分辨率的可控有限宽度区域。
本文为了提高AMR水平集方法的迭代效率,在采用了局部水平集方法的基础上结合了窄带法[21]对需要标记的区域进行选择,优化了细化区域的选择机制。同时,采用基于red-green细化的改进算法优化了T节点的近似计算。最后,为验证所提出算法的效果,将该算法应用于基于水平集的血栓生长模型中,优化了模型中水平集求解部分,并利用该模型进行了血栓形成过程的仿真实验。
1 局部水平集方法基本原理水平集方法[22]在解决轮廓演化问题时,把低维的计算问题上升到高一维,即把N维的轮廓利用N+1维的水平集函数进行描述,获得一个闭合的超曲面,水平集函数值为0的零水平集即为被描述的轮廓。这样,轮廓的运动就可以通过闭合超曲面的演化方程得到,仅需要确定演化过程中零水平集的位置就可对给定轮廓进行追踪。
局部水平集的基本思想是在零水平集周围设定一条覆盖零水平集的带状区域,区域内的水平集符合|ϕ|<K,2K即为窄带宽度。因为曲线在演化过程中每个时间步中的移动距离较小,所以不需要对水平集方程在整个定义域内进行计算,仅需要在窄带区域进行计算,从而降低计算的时间复杂度。假设一副二维图像的网格大小为N×N,节点数为N2。用传统水平集方法对图像的轮廓进行追踪,那么将二维图像处理上升为三维函数的演化问题,每个时间步中水平集函数计算的时间复杂度为O(N2)。而局部水平集可以将单位时间内的计算量下降到O(kN),k则表示在窄带内部像素点的数量。窄带的引入大大减少了曲线演化的时间,使计算效率得到有效提高。
在局部水平集方法[23]中,局部水平集方程被定义为
| $ \frac{{\partial \phi }}{{\partial t}} + C(\phi )\vec F \cdot \mathit{\nabla } \phi = 0, $ | (1) |
其中:ϕ(x, t)是局部水平集函数;截断函数C(ϕ)为
| $ C(\phi ) = \left\{ {\begin{array}{*{20}{l}} {1, }&{\;\;\;|\phi | > \mathit{\Delta } , }\\ {\frac{{{{(|\phi | - \delta )}^2}(2|\phi | + \delta - 3\mathit{\Delta } )}}{{{{(\delta - \mathit{\Delta } )}^3}}}, }&{\mathit{\Delta } < |\phi | \le \delta , }\\ {0, }&{\;\;\;|\phi | > \delta , } \end{array}} \right. $ | (2) |
水平集的初始化仅在T0={x:|ϕ(x)<δ|}处进行。
2 Red-green混合细化方法本节将对现有的red-green及改进后的red-green分别进行细化描述。
2.1 传统的red-green细化Red-green细化最初由文献[11]提出,是一种基于三角网格的局部细化方法。它的实质是用两种不同的策略对单元格进行细化,从而减少T节点。随着三维网格的发展,这种red-green技术也适用于三维四面体网格[16-18]。二维三角网格分割的red细化策略和green细化策略如图 1所示。从图 1(a)可知二维的red细化(也称为正则细化)是通过连接边的三个中点将一个三角形分成四个子三角形(称为红色元素)。从图 1(b)可知green细化(也称为不规则求精)是连接顶点和与之相对的边的中点,通过green细化分割获得的两个子三角形称为绿色元素,两条分割边P3P1和P1P4称为绿色边(或不规则边)。元素T=T1∪T2∪T3∪T4的red细化为四个全等子域T1,T2,…,T4;元素T=T1∪T2的green细化为两个子三角形T1和T2。
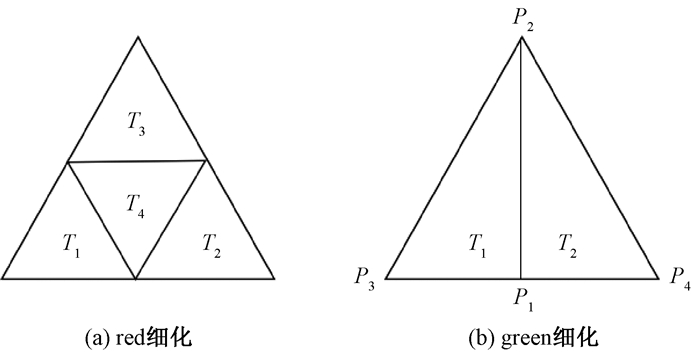
|
图 1 传统的red-green细化示意图 Fig. 1 The diagram of traditional red-green refinement |
Red细化策略的优势在于,可以保证细化得到的子网格的形状与原始网格比较接近,但是会产生较多的T节点,在计算时增加难度;Green细化策略可以减少T节点的产生,但是不能保证子网格的形状。因此,需要将两种策略结合使用。
2.2 无T节点四边形网格的局部细化原始的四边形网格细化一直使用四等分作为red细化策略。在实际应用中,如果每个边上最多允许一个T节点存在,red细化的对分完全可以满足四边形网格上的局部细化。但是在实际的计算中,T节点数量的增加会导致计算难度的升高。在数值算法中,为了保持离散解的连续性,必须对T节点施加约束。为了尽量减少求解过程中对T节点特殊处理,Bank等[11]给出了green细化策略,它们直接将T节点与四边形顶点相连。由于T节点出现在边的中间,在将T节点与不相邻顶点相连的情况下,即使初始网格为四边形,三角形仍将出现在细化网格中,生成的三角形和四边形的混合网格需要较为复杂的数据结构进行描述。因此,将red细化和green细化结合后可以形成新的混合细化,首先构造合适的red细化策略,保证细化网格与原始网格的一致性,然后辅助green细化策略进一步减少T节点的数量。同时,将混合细化方法扩展到四边形以消除T节点。
如图 2所示,在二维混合细化算法中,原始网格首先通过三等分单元格K的边,将其分割为9个子单元格K1, K2, …, K9进行red细化。内部节点P5、P6、P7、P8相对原始单元格顶点P1、P2、P3、P4的位置如下:
| $ {P_5} = \left( {4{P_1} + 2{P_2} + {P_3} + 2{P_4}} \right)/9; $ | (3) |
| $ {P_6} = \left( {2{P_1} + {P_2} + 2{P_3} + 4{P_4}} \right)/9; $ | (4) |
| $ {P_7} = \left( {2{P_1} + 4{P_2} + 2{P_3} + {P_4}} \right)/9; $ | (5) |
| $ {P_8} = \left( {{P_1} + 2{P_2} + 4{P_3} + 2{P_4}} \right)/9, $ | (6) |
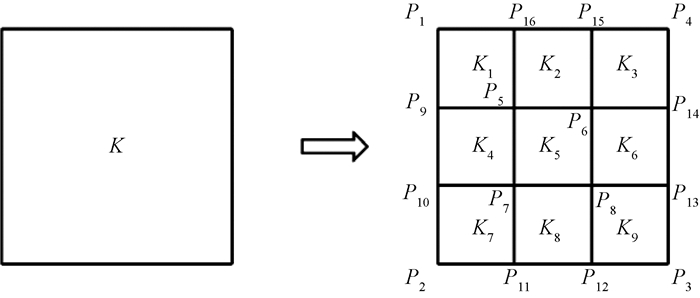
|
图 2 Red细化 Fig. 2 Red refinement |
其中Pi=(xi, yi),i=1, 2, …, 8为坐标。
如图 3所示,处于细化边缘的非细化单元格根据邻接网格的细化情况可以分为四种模式:三侧细化;相对两侧细化;相邻两侧细化和单侧细化,分别对应产生6个、4个、4个、2个T节点(实心圆)。消除这些T节点的方案之一是该非细化网格进行同样的red细化(虚线),但会产生新的T节点,数量分别是2个、4个、4个、6个(空心圆)。该方案仅对三侧细化模式具有减少T节点的效果。根据文献[11]提出的“Ke-1 Neighbor规则”,后三种情况需要采用green细化(实线)来消除T节点。
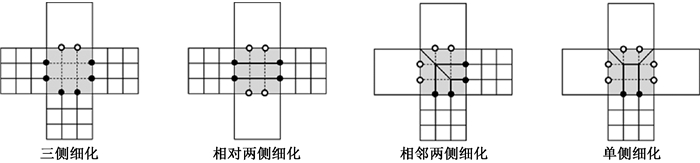
|
图 3 边缘单元格的不同细化情况及相应的green细化模式 Fig. 3 The different adjacent refinement of edge cells and the corresponding green refinement mode |
当使用局部水平集方法对水平集函数进行演化时,只需要更新窄带内节点的水平集。水平集方程可采用WENO方法在空间上进行离散求近似解。WENO[24]是由ENO格式发展而来的重构或插值过程。WENO中的单侧后导数Dx-ϕ和前导数Dx+ϕ的近似值为
| $ D_x^ - \phi = D_x^ + \phi = {\omega _1}\phi _x^1 + {\omega _2}\phi _x^2 + {\omega _3}\phi _x^3, $ | (7) |
该方法求解水平集方程ϕi时需要使用{ϕi-3, ϕi-2, ϕi-1, ϕi, ϕi+1, ϕi+2, ϕi+3}。根据求解方法的精度不同,求解过程中使用的相邻节点水平集数量也不同。对于非均匀细化笛卡尔网格,两级细化分界处的单元格的T节点处,由于相邻数据不连续,需要通过与其相连节点的ϕ值求得近似相邻数据,用于水平集方程求解。
为了消除T节点带来的附加计算,我们将改进后的red-green细化与窄带法相结合。首先对窄带区域内部的节点进行red细化,并对靠近窄带边界的节点进行green细化,以消除T节点。
如图 4所示,深色区域为red细化网格,浅色为green细化网格,判断原始网格的“分类”:
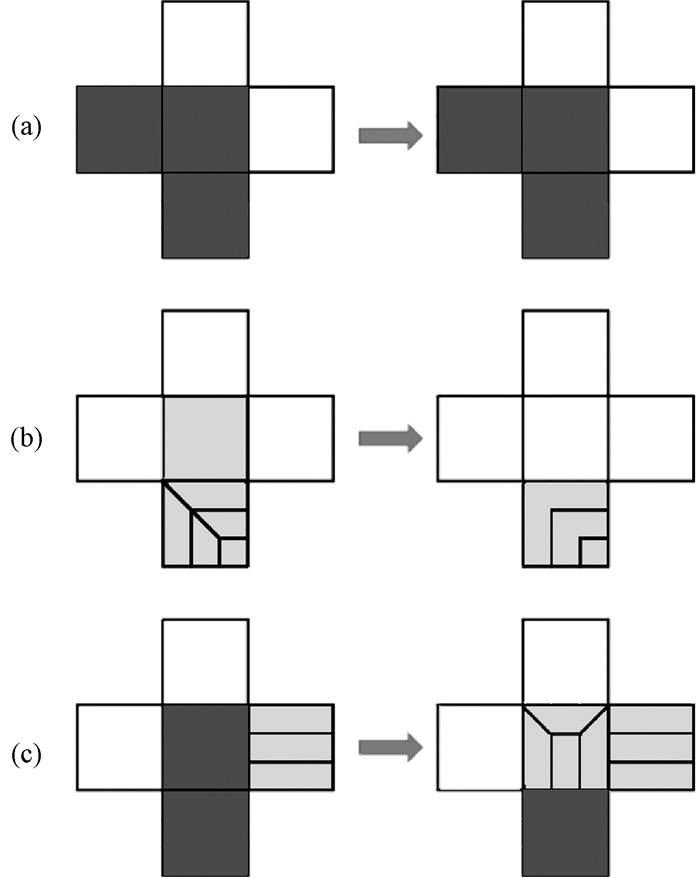
|
图 4 网格细化过程示例图 Fig. 4 Example diagram of mesh refinement process |
1) 与red细化相邻的原始单元格称为红色元素(图 4(a));
2) 与green细化相邻的原始单元格称为绿色元素(图 4(b));
3) 同时与red细化网格和green细化网格相邻的原始网格,也将其看作红元素(图 4(c))。
图 4中red细化网格和红色元素为深色,green细化网格和绿色元素为浅色。然后,忽略绿色元素,仅针对每一个红色元素进行如下操作:
1) 统计红色元素边上的T节点数n;
2) 将红色元素进行“预red细化”,统计细化后新增T节点数m;
3) 若m/n<1,对该红色元素实施red细化,否则实施相应的green细化。
3 基于水平集的血栓形成计算模型血栓[25]是血液循环中血管表面或心脏内壁上形成的凝块或沉积物。当血管内膜受损时,内皮下基质暴露,损伤附近的血小板被激活。随着血小板的粘附和聚集,形成以血小板为主要成分的初期血栓。根据血栓形成的原理,我们设计了初期血栓的混合模型,如图 5所示。血栓生长模型包括血管、破损的血管内膜、血小板、血浆和初期血栓,在设计成管状的血管中,血浆自左向右流动,带着血小板,经过破损的血管内膜这一区域的血小板被凝血因子激活,然后成为初期血栓的一部分。
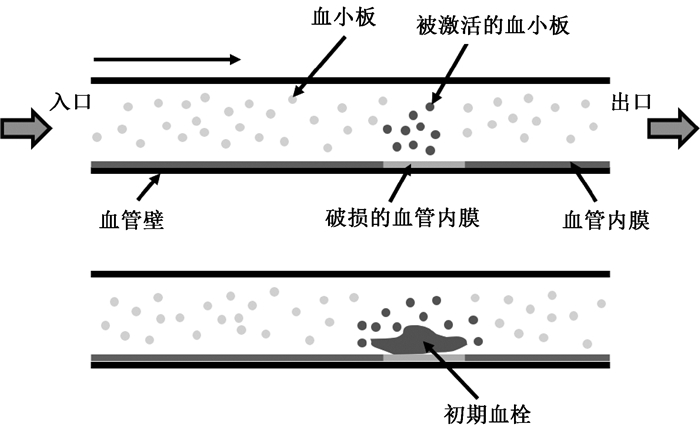
|
图 5 血栓生长模型示意图 Fig. 5 Schematic diagram of thrombus growth model |
血栓生长计算模型包括血浆、血小板和血栓三部分。如图 6所示三个子模型的结构和关系:血浆子模型提供血流速度场并输送血小板;血小板模型是用来模拟血小板粘附和聚集的过程;血小板通过血栓子模型合并到血栓中。我们将初期血栓的表面定义为零水平集,并通过水平集方法追踪界面位置的变化,窄带的宽度值与血小板的直径成正比,确保新粘附上的血小板可以被包含在窄带内。
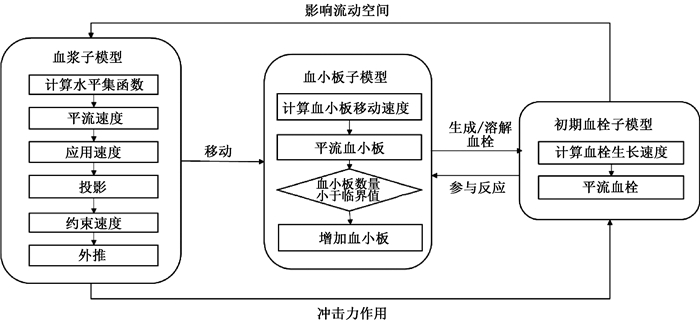
|
图 6 血栓生长计算模型结构图 Fig. 6 Structure diagram of thrombus growth calculation model |
血浆子模型是用来模拟血液流动的子模型,提供了血液流速,并且负责运输血小板。我们假设血浆是不可压缩的,通过求解Navier-Stokes方程获得血流速度。血小板是初期血栓的主要组成部分。血小板模型用于模拟血小板的激活、粘附和聚集反应。分别计算血小板在血流冲击力、破损内膜粘附力和初期血栓的聚集力作用下的移动速度,并使血小板在该速度下移动。
模拟血栓生长过程的子模型中,我们将血栓的表面定义为由零水平集描述的自由移动界面,水平集ϕ由符号距离公式计算得出:血栓内部ϕ<0;血栓外部ϕ>0;血栓表面ϕ=0。将破损表面定义为初期血栓的初始表面。在血栓生长过程中,发生粘附和聚集的血小板被定义为组成初期血栓的一部分,因此,当血小板模型中判定某一血小板发生粘附或聚集后,在该血小板所在位置定义界面移动速度,使血栓表面向外扩张产生扩张的表面通过水平集方法追踪界面位置的变化。在追踪过程中,定义窄带的宽度值不小于血小板的直径,以确保新捕获的血小板完全包含在窄带内。
4 实验结果与分析为了验证改进的red-green细化策略在局部水平集中的有效性,我们建立了不同分辨率下的轮廓和窄带,并对细化数据进行统计并加以分析。在边长为5 mm的正方形网格中,建立半径为15 mm的圆形轮廓,窄带宽度为0.2 mm。网格的分辨率从25*25开始,以25为间隔递增至200*200。网格中red细化单元格数、red细化后T节点数和追加green细化单元格数的变化曲线如图 7所示。随着分辨率的提高,被细化的网格数增长幅度非常大。由于圆形轮廓较为简单,T节点数目虽然增长,但幅度相对较小。消除这些red细化出现的T节点所追加的green细化单元格数目的增长幅度小于T节点的增长幅度,说明green细化在有效消除T节点时并不会带来更多的计算量。
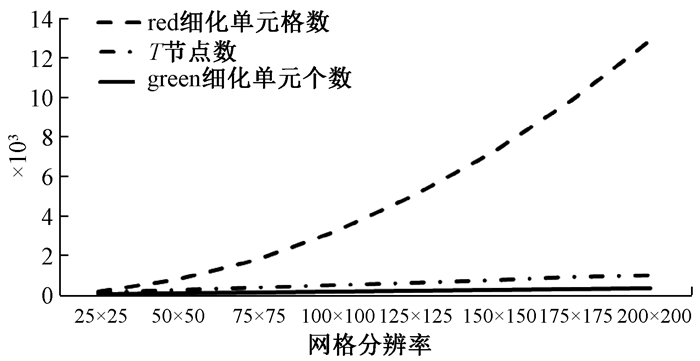
|
图 7 不同分辨率下细化单元格数及T节点数变化曲线 Fig. 7 Variation curve of refined cell number and T-node number under different resolutions |
同时,针对静脉,我们使用第3节介绍的计算模型分别在无狭窄的直血管和有部分平滑狭窄的血管中对血栓的形成过程进行了仿真实验,各项血管参数分别为:血流速度1 m/s;血液黏度3.5×10-4 Pa ·s;血管直径4 mm;血管长度12 mm;破损区域面积1.57 mm×2 mm;狭窄程度25%;狭窄长度2 mm。并利用视觉化工具函式库(Visualization Toolkit,VTK)将仿真实验的结果进行可视化,方便观察血栓的形成过程,图 8为两种血管的形态及破损血管内壁的位置的可视化图像。破损内壁初始为光滑表面,随着血小板被破损血管壁捕获成为血栓,表面不断扩展,形成增多并叠加的颗粒状突起。

|
图 8 仿真血管 Fig. 8 Simulated blood vessels |
在无狭窄血管和有狭窄血管中将血流速度都分别设置为三种情况:2 mm/s,4 m/s和6 m/s(对应雷诺数Re分别为0.01、0.02和0.03),分别进行5次时长为50 ms的血栓生长仿真实验,将平均结果绘制生长曲线,如图 9所示。狭窄血管中的生长速度总体大于无狭窄血管,两种血管中的血栓生长均随血流速度增加变快。将该结果与Kamada等的静脉血栓仿真[26]结果对比,血栓生长速率以及该速率与雷诺数的关系是一致的。不同之处在于,Kamada实验中考虑了血栓脱落,生长曲线存在中断,讨论脱落栓子阻塞血管的危险性,本文期望观察血栓在出现位置处的阻塞情况,未考虑血栓脱落,因此血栓在整个仿真时间内持续上升。
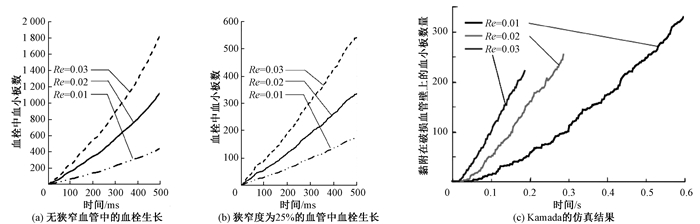
|
图 9 不同血流速度下血栓生长曲线图 Fig. 9 Thrombus growth curve under different blood flow velocity |
根据仿真过程中网格数据的比较,如图 10所示,无论是否存在狭窄,如果在目标区域中使用均匀细化,即在覆盖全部血栓的区域建立六面体网格,细化网格的数量和增长率远高于基于窄带方法的局部细化。使用局部细化后,局部细化网格中仍存在约10%的T节点,求解演化方程时需要分别计算。引入green细化之后,尽管细化网格的总数增加了约3%,但green细化网格的数量仍小于T节点的数量。同时,在统计增长率中,发现尽管在狭窄血管的模拟中细化网格的总数大于非狭窄血管的数目,但其增长率小于非狭窄血管的增长率。这表明由于血管几何结构的复杂性,细化网格的数量仅在狭窄初期才大,但是在血栓生长过程中细化网格的数量却缓慢增加。由于窄带方法的局部细化是基于零水平集界面,该模型中的零水平集是血栓表面,细化网格也是血栓表面的增长。因此,在狭窄的情况下,细化网格的缓慢生长速度表明由于血管狭窄所导致的血小板颗粒的粘附和聚集范围更加集中。
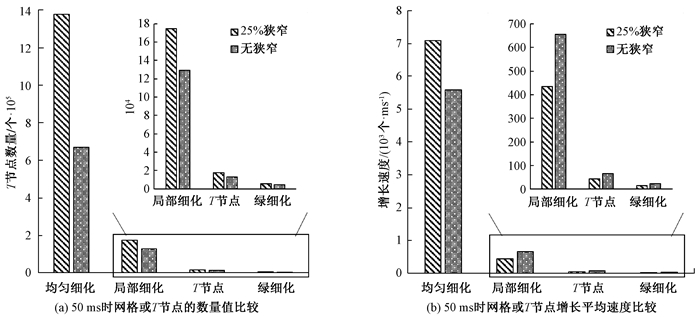
|
图 10 仿真实验中随血栓生长的网格数据比较 Fig. 10 Comparison of grid data with thrombus growth in simulation experiment |
本研究中,我们将改进后的red-green细化策略融合到局部水平集中,有效地提高了笛卡尔网格的运算效率。一方面,red-green细化的使用消除了T节点,避免了由于找不到邻居节点导致的计算难度的增加,提高了计算效率;另一方面,窄带法的应用,使得每个时间步后,只需要对窄带内的点进行是否需要细化或粗化的判断,定义在零水平集上的速度函数也只需要扩展到窄带内的部分,降低水平集方法的计算量和存储空间。我们先是使用简单的圆形轮廓对其进行实验,又将该方法应用与血栓生长过程的建模和仿真中。实验结果表明改进后的算法在网格分辨率增加时能够更好地减少计算量,并能够有效地提高计算效率。该方法对于血栓生长过程的建模与仿真有利于进一步分析血栓形成的相关影响因素。本文研究中,在选择细化区域时仅考虑了与零水平集的距离,未充分考虑轮廓形态的复杂程度。我们下一阶段的工作将继续针对自适应细化网格进行研究,将能够代表轮廓几何特征的曲率等元素加入判断细化区域的特征参数中。
| [1] |
OSHER S, SETHIAN J A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations[J]. Journal of computational physics, 1988, 79(1): 12-49. DOI:10.1016/0021-9991(88)90002-2 (  0) 0) |
| [2] |
OSHER S, FEDKIW R. Level set methods and dynamic implicit surfaces[M]. New York: Springer, 2003.
(  0) 0) |
| [3] |
吕文鹏, 许峰. 基于自适应网格方法的免疫多目标进化算法[J]. 软件工程, 2018, 21(6): 25-28. LV W P, XU F. An immune multi-objective evolutionary algorithm based on the adaptive grid method[J]. Software engineering, 2018, 21(6): 25-28. (  0) 0) |
| [4] |
殷亚军, 李阳东, 涂志新, 等. 基于八叉树自适应网格技术的Level Set运动界面追踪方法[J]. 化工学报, 2016, 67(11): 4732-4741. YIN Y J, LI Y D, TU Z X, et al. Interface capturing method based on Level Set with octree adaptive mesh technology[J]. CIESC journal, 2016, 67(11): 4732-4741. (  0) 0) |
| [5] |
段献葆, 党妍, 秦玲. Stokes问题形状优化中自适应水平集方法的应用[J]. 上海大学学报(自然科学版), 2020, 26(4): 671-680. DUAN X B, DANG Y, QIN L. Application of adaptive level set method in shape optimization for Stokes problem[J]. Journal of Shanghai university (natural science edition), 2020, 26(4): 671-680. (  0) 0) |
| [6] |
裴红星, 刘金达, 葛佳隆, 等. 图像拼接技术综述[J]. 郑州大学学报(理学版), 2019, 51(4): 1-10, 29. PEI H X, LIU J D, GE J L, et al. A review on image mosaicing techniques[J]. Journal of Zhengzhou university (natural science edition), 2019, 51(4): 1-10, 29. (  0) 0) |
| [7] |
PLAZA A, CAREY G F. Local refinement of simplicial grids based on the skeleton[J]. Applied numerical mathematics, 2000, 32(2): 195-218. DOI:10.1016/S0168-9274(99)00022-7 (  0) 0) |
| [8] |
HUAYTA O A, RIVARA M C. Study on the average size of the longest-edge propagation path for triangulations[C]// Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications. Malta: Science and Technology Publications, 2020: 368-375.
(  0) 0) |
| [9] |
ARNOLD D N, MUKHERJEE A, POULY L. Locally adapted tetrahedral meshes using bisection[J]. SIAM journal on scientific computing, 2000, 22(2): 431-448. DOI:10.1137/S1064827597323373 (  0) 0) |
| [10] |
BORKER R, HUANG D, GRIMBERG S, et al. Mesh adaptation framework for embedded boundary methods for computational fluid dynamics and fluid-structure interaction[J]. International journal for numerical methods in fluids, 2019, 90(8): 389-424. DOI:10.1002/fld.4728 (  0) 0) |
| [11] |
BANK R E, SHERMAN A H, WEISER A. Refinement algorithms and data structures for regular local mesh refinement[M]. Amsterdam: North-Holland Publishing, 1983: 3-17.
(  0) 0) |
| [12] |
BANK R E. The efficient implementation of local mesh refinement algorithms[M]. Babuska: Springer Vienna, 1983: 74-81.
(  0) 0) |
| [13] |
CERVENKA J. Three-dimensional mesh generation for device and Process simulation[EB/OL]. [2020-11-28]. http://www.iue.tuwien.ac.at/phd/cervenka/node14.html.
(  0) 0) |
| [14] |
RIVARA M C, VEMERE M. Cost analysis of the longest-side (triangle bisection) refinement algorithm for triangulations[J]. Engineering with computers, 1996, 12(3/4): 224-234. (  0) 0) |
| [15] |
ROSENBERG I G, STENGER F. A lower bound on the angles of triangles constructed by bisecting the longest side[J]. Mathematics of computation, 1975, 29(130): 390. DOI:10.1090/S0025-5718-1975-0375068-5 (  0) 0) |
| [16] |
BEY J. Tetrahedral grid refinement[J]. Computing, 1995, 55(4): 355-378. DOI:10.1007/BF02238487 (  0) 0) |
| [17] |
BEY J. Simplicial grid refinement: on Freudenthal's algorithm and the optimal number of congruence classes[J]. Numerische mathematik, 2000, 85(1): 1-29. DOI:10.1007/s002110050475 (  0) 0) |
| [18] |
MOLINO N, BRIDSON R, TERAN J, et al. Red green strategy for meshing highly deformable objects with tetrahedra[EB/OL]. (2003-01-01)[2021-01-26]. https://www.researchgate.net/publication/247367408_Red_green_strategy_for_meshing_highly_deformable_objects_with_tetrahedra.
(  0) 0) |
| [19] |
ADALSTEINSSON D, SETHIAN J A. A fast level set method for propagating interfaces[J]. Journal of computational physics, 1995, 118(2): 269-277. DOI:10.1006/jcph.1995.1098 (  0) 0) |
| [20] |
PENG D P, MERRIMAN B, OSHER S, et al. A PDE-based fast local level set method[J]. Journal of computational physics, 1999, 155(2): 410-438. DOI:10.1006/jcph.1999.6345 (  0) 0) |
| [21] |
SOCHNIKOV V, EFRIMA S. Level set calculations of the evolution of boundaries on a dynamically adaptive grid[J]. International journal for numerical methods in engineering, 2003, 56(13): 1913-1929. DOI:10.1002/nme.641 (  0) 0) |
| [22] |
CHOPP D L. Computing minimal surfaces via level set curvature flow[J]. Journal of computational physics, 1993, 106(1): 77-91. DOI:10.1006/jcph.1993.1092 (  0) 0) |
| [23] |
ZHANG W H, ZHANG Y T. Efficient local level set method without reinitialization and its appliance to topology optimization[J]. Mathematical problems in engineering, 2016, 1-14. (  0) 0) |
| [24] |
白晓雅, 郑秋亚, 梁益华. 求解欧拉方程的嵌入WENO格式[J]. 郑州大学学报(理学版), 2020, 52(3): 98-103. BAI X Y, ZHENG Q Y, LIANG Y H. The embedded WENO scheme for solving the Euler equation[J]. Journal of Zhengzhou university (natural science edition), 2020, 52(3): 98-103. (  0) 0) |
| [25] |
李丽娟, 梁珊, 何亚州, 等. 血小板自噬在动脉血栓形成中的作用研究进展[J]. 重庆医学, 2019, 48(3): 70-472. LI L J, LIANG S, HE Y Z, et al. The research progress of platelet autophagy in the formation of arterial thrombosis[J]. Chongqing medicine, 2019, 48(3): 70-472. (  0) 0) |
| [26] |
KAMADA H, TSUBOTA K I, NAKAMURA M, et al. A three-dimensional particle simulation of the formation and collapse of a primary thrombus[J]. International journal for numerical methods in biomedical engineering, 2010, 26(3/4): 488-500. (  0) 0) |
 2022, Vol. 54
2022, Vol. 54


