人类的步态包含非常独特的模式,可用于身份的识别和验证.加速度传感器以其低廉的价格、较高的灵敏度和较小的体积被广泛应用于智能手机中.其具有的独特优势使研究人员认识到它在基于步态身份识别领域的应用前景.基于步态的身份识别主要难点和重点集中在特征提取和分类识别方法上,特征提取是为了从步态加速度传感器信号中提取可以表征人体身份的特征向量,是基于智能手机传感器用户身份识别技术中的关键所在,其效果会直接影响分类器的识别率.其中,基于加速度信号特征提取的方法可以分为时域分析法、频域分析法和时频域分析法.文献[1-3]中只在时域阶段提取了简单特征,虽然计算量小,但是所取得的识别率并不是很高.文献[4-6]添加了频域的特征,其识别率得到了很大的提高,但是整体的特征维数较高,需要对特征进行降维或优化处理,其处理效果又直接影响最终的结果.文献[7]引入了时-频分析方法,能够在时间和频率两个空间内更好地观察信息特性,但冗余度较大.随着基于加速度传感器步态身份识别研究的不断深入,研究人员不断尝试通过提取新的特征来提高身份识别率.
傅里叶描述子[8-9]是一种新型的描述图像特征的数学方法,已成功运用于图形图像领域中的曲线轨迹形状匹配.因此,可以根据步态加速度数据在时域的曲线图,将步态身份识别问题转换为轨迹曲线形状的匹配问题.从图像学角度出发,本文利用傅里叶描述子来描述步态曲线的较粗轮廓的全局轨迹曲线特征,并提出方向角描述子的概念来进一步刻画步态曲线细致的局部轨迹曲线特征,最后将二者结合完成步态轨迹曲线的匹配.结果表明,本文所提出的步态轨迹曲线特征能够很好地用于身份识别.本文在步态身份识别中的主要工作如下.
1) 提出将步态身份识别问题转换为步态加速度数据的平面轨迹曲线匹配问题.
2) 傅里叶描述子是粗轮廓的特征,在局部细节特征方面描述不足,本文提出用方向角描述子来描述曲线的局部轨迹曲线特征.
3) 轨迹曲线特征不同于传统的时域统计特征,本文将两者相结合取得了较高的识别率.
1 步态特征提取方法观察步态加速度数据在时域上的曲线形状,发现同一个人的步态曲线具有较大的相似性,而不同人的步态曲线具有较大的差异性.之前的身份识别研究工作中,大多数方法都是直接从步态数据本身出发.对于最能反映步态曲线的形状特征却没有深入的研究,事实上,形状是最能反映其变化的特征.因此,本文从图像学形状角度出发,根据步态轨迹曲线特征来完成身份识别.
1.1 标准步态曲线获取手机中的加速度传感器值分为3个方向,即X、Y、Z3个轴,3个轴的数据是相对手机的3个方向,为消除方向的影响,本文使用合加速度a.
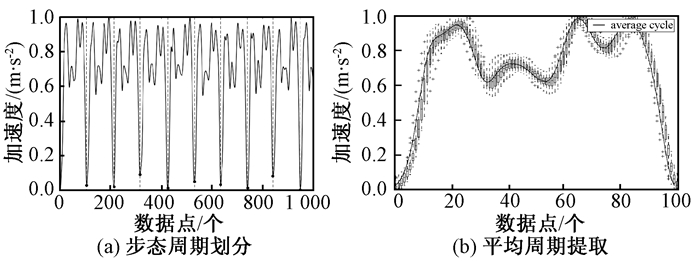
已知步态数据是时变的周期信号,为了减少计算量,本文只考虑步态的单个周期.具体周期分割如图 1(a)所示,图 1(a)是以极小值点为周期的分割点.在实际数据采集中,步态序列包含多个周期,在开展后期工作前,需要提取单个标准周期,使得该周期能够表征整个步态特征.本文参照文献[3]的方法提取周期,然后使用平均周期作为标准周期,如图 1(b)所示.图 1(b)表示多个周期叠加的箱线图,黑实线表示平均周期.
|
图 1 标准步态周期提取 Figure 1 Standard gait cycle extraction |
本文提出将轨迹曲线特征和统计特征相结合用于身份识别.因此,统计特征的选择至关重要.而大多数传统的统计特征方法是直接从时域或频域上提取诸如均值、标准差、最大值、最小值、偏度、峰度、四分位差、峰值数量、均方根等特征值,再通过特征值进行身份识别.实际上不是选取的特征越多,识别率就越高.所以,本文采用了一种自底向上、逐步合并的特征聚合方法[10].
1.3 轨迹曲线特征提取人在行走过程中的步态曲线反映了人在行走过程中的步态特征,这些步态曲线更好地展现了每个人的行走姿势,并且能够很好地表征步态数据的结构、轨迹形状等一些重要的信息.所以可将不同人员的步态轨迹曲线特征作为判别一个人身份识别的条件之一.
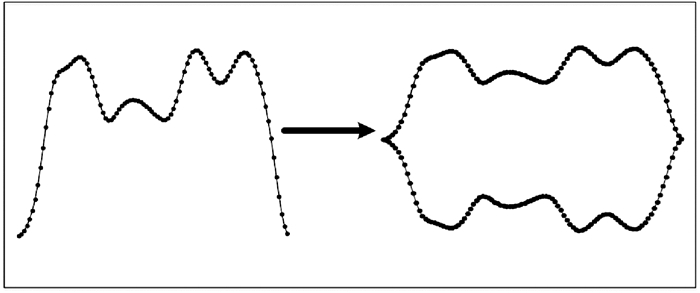
1.3.1 非闭合步态曲线的闭合化操作步态时序曲线是一条未封闭的曲线,而傅里叶描述子不能对非闭合曲线轮廓特征进行描述,因为非闭合曲线首尾两点信号不连续,会导致信号不连续.为了能够使用傅里叶形状描述子模型进行曲线轮廓提取,本文将非闭合步态曲线闭合化操作.对首尾点做连线并以此连线为轴进行镜像处理,构成封闭的曲线,镜像部分与原曲线形状完全相同,可视为原曲线的对偶形状(首尾曲线坐标不是原点的连线,而是曲线首尾坐标的连线).如图 2所示,非闭合步态曲线经过镜像处理形成一条封闭的步态曲线.
|
图 2 步态曲线封闭处理 Figure 2 Closed treatment of gait curve |
傅里叶描述子是一种基于频域变换的形状表示算法.经过大量的实验研究表明,傅里叶描述子对轨迹曲线特征有很强的描述和识别的能力,并且计算简单、运行速度快、精度较高.首先将轮廓曲线表示成1个一维的封闭的曲线函数,可以表示为以周长为周期的函数.然后对此封闭的轮廓曲线函数进行傅里叶变换,傅里叶变换中的一系列的级数被称为傅里叶形状描述子.
假设在xy平面上有N个坐标点,P0, P1, P2, …, PN-1为该封闭曲线上的点,以P0为起始点,PN-1为结束点(P0=PN-1),以顺时针方向经过P0(x0, y0), P1(x1, y1), …, PN-1(xn-1, yn-1)后可回到原始位置,并可反复循环.设x(k)=xk, y(k)=yk, 所以一条封闭曲线的边界点可表示为Z(k)=(x(k), y(k)), k=0, 1, …, N-1, 每一个坐标又可以处理成复数的形式Z(k)=X(k)+jY(k), k=0, 1, 2, …, N-1,X(k)为复数坐标的实部;Y(k)为复数坐标的虚部.
| $ X\left( k \right) = {x_i} + \frac{{{x_{i + 1}} - {x_i}}}{{{S_{i + 1}} - {S_i}}}(k - {S_i}), Y\left( k \right) = {y_i} + \frac{{{y_{i + 1}} - {y_i}}}{{{S_{i + 1}} - {S_i}}}(k - {S_i}), $ |
其中Si(0≤i≤N-1)为点Pi到起始点P0的曲线长,并且Si≤k≤Si+1, 0≤i≤N-1.函数的傅里叶级数表达式为
| $ {C_n} = \frac{1}{L}\{ {x_i} + \frac{{{x_{i + 1}} - {x_i}}}{{{S_{i + 1}} - {S_i}}}(k - {S_i}) + {\rm{j}}[{y_i} + \frac{{{y_{i + 1}} - {y_i}}}{{{S_{i + 1}} - {S_i}}}(k - {S_i})]\cdot{{\rm{e}}^{ - {\rm{j}}\frac{{2n{\rm{ \mathsf{ π} }}x}}{L}}}{d_k}\} . $ |
傅里叶级数的各项系数Cn为复数,模向量C=(‖c1‖, ‖c2‖, …, ‖ck‖),向量C与形状的尺度、方向和选择的起始点有关,为了使其具有选择、平移和尺度的不变性,则需要对C进行归一化处理,得到傅里叶形状描述子.归一化后的傅里叶形状描述子为d(i)=‖c(i)‖/‖c(1)‖, i=1, 2, …, K.
由于步态轨迹曲线的全局特征大都集中在低频部分,而高频部分体现步态轨迹曲线的细节特征.系数选择得越多,变换后的数据与原数据的误差越小,但本文的目的在于分类识别,而不在于精确的原数据重构,而且选择的系数越多并不代表识别的效果越好.根据实验,论文选取前15个低频傅里叶系数,它们对应着目标的总体轨迹形状特征,用FD表示此部分提取的特征集合.
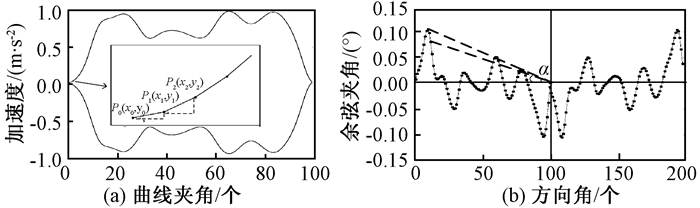
1.3.3 方向角描述子傅里叶描述子隐藏了空间域中的位置信息,往往更倾向于表现全局特征.为了弥补傅里叶描述子在局部表征上的欠缺,本文提出了方向角描述子概念.角度特征不仅能够描述方向变化的特征,也具备旋转不变性原则.首先计算步态曲线轨迹上所有点方向角序列,如图 3所示.并得到所有角度点切线以及方向角序列的质心,利用角度点切线与质心的夹角描述曲线轨迹的变化.图 3(a)表示曲线上各个点的余弦夹角,图 3(b)表示由一系列余弦夹角组成的夹角序列.设曲线轨迹有N个数据点,则有N-1个角度点,则角度可表示为
| $ \left\{ \begin{array}{l} {x_z} = \sum\limits_{i = 1}^{N - 1} {{x_i}, } \\ {y_z} = \sum\limits_{i = 1}^{N - 1} {{y_i}.} \end{array} \right. $ |
|
图 3 方向角描述子 Figure 3 Direction angle descriptor |
则每个角度点到其质心的距离r可以用欧氏距离表示为
| $ \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{D}}^1}}& \ldots &{\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{D}}^N}}\\ {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{D}}^1}}& \ldots &{\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{D}}^N}} \end{array}} \right] $ |
其中:N表示第N个周期;FD表示傅里叶描述子的形状轮廓特征;AD表示角度变化特征.
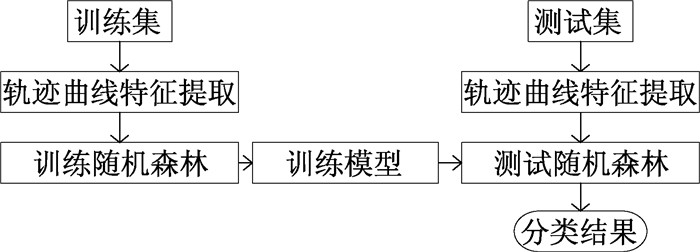
2 基于步态特征的身份识别随机森林算法是采用自主聚类把多个不同的决策树集成为一个学习机的集成学习方法.Bagging方法从全部的训练样本集合中通过可重复采样技术得到不同的训练子集,利用随机产生的多个训练样本子集训练模型,生成多个相应的决策树.在分类识别时,对每个决策树的分类结果进行投票,取票数最多的类别作为测试数据的最终类别[11].本文提出的基于步态特征的身份识别方法的框架结构如图 4所示.该方法包括两个阶段:训练阶段和测试阶段.在训练阶段,将步态的轨迹曲线特征用训练随机森林分类器进行训练,产生训练模型;在测试阶段,对测试数据获取轨迹曲线特征后,基于训练阶段产生的训练模型利用测试随机森林分类器通过投票产生分类结果.
|
图 4 基于随机森林的步态识别方法框架 Figure 4 Gait recognition method framework based on random forest |
仿真设置:选用三星Note Ⅱ手机采集加速度步态数据,内置传感器的采样数据频率为100 Hz,以Python 2.7作为仿真平台,硬件平台处理器为Intel Core i5 CPU,2.20 GHz,内存4 GB,操作系统环境为Windows 8.1,64位.采集40名健康志愿者的原始加速度数据,平均年龄为23~26岁,身高为155~185 cm.全体志愿者将设备放置在裤子前面的右侧口袋中,并且手机的屏幕朝外.以正常速度在平地上行走大约200 m,对每人采集数据30次.
3.2 实验结果及分析本文参照文献[12]使用十折交叉验证,将数据集进行分组,一部分作为训练集,另一部分作为测试集.通过4组实验对本文的方法进行验证.
3.2.1 第1组实验为了证明轨迹曲线特征(傅里叶描述子、角度描述子)的有效性及鲁棒性.分别在4组不同的数据集上进行验证,结果如表 1所示.分别使用傅里叶描述子和角度描述子作为特征在4组不同的数据集上进行验证.实验的正确识别率都不是很高,主要因为步态轨迹曲线并不是稳定不变的,利用轨迹曲线形状进行匹配识别很大程度上受到曲线本身的限制,但依旧可以验证使用轨迹曲线特征用于身份识别的有效性及强鲁棒性.
|
|
表 1 不同数据集上轨迹曲线特征的验证 Table 1 Verification of trajectory curve characteristics in different data sets |
为进一步提高识别率,本文将轨迹曲线特征和统计特征相结合.提取的统计特征[2-4, 7-14]以及选取的几种特征组合如表 2所示.
|
|
表 2 常见特征及标号 Table 2 Common features and labels |
在步态识别中使用的步态特征大都基于时域或频域以及二者结合,该类特征提取方便,计算简单.同时根据表 3发现,不是提取的特征越多分类的效果就越好,从中选取有效的特征至关重要.因此,本文使用1.2中的特征提取方法从表 2中提取有效的统计特征,结果如表 4所示.
|
|
表 3 提取的特征值及识别率 Table 3 Extraction of eigenvalue and recognition rate |
|
|
表 4 随机森林算法的特征选择过程表 Table 4 Feature selection process table of random forest algorithm |
由表 4可知:选取1, 2, 3, 5, 6, 7, 8, 9, 13, 15特征时取得的分类识别率最高,达到88.40%.因此本文选取上述特征作为统计特征.
3.2.3 第3组实验根据第1组的轨迹曲线特征,第2组的统计特征,该部分实验用于验证轨迹曲线特征及组合特征的识别率(本文使用表 1中的数据集2,采用十折交叉验证).结果如表 5所示.单独使用其中任一轨迹曲线特征,正确识别率不是很高,将两种特征相结合能有效地提升正确识别率.但轨迹曲线特征不同于传统的时域统计特征,其性能会受到曲线自身特性的制约.因此,本文将二者相结合,识别率提升近2%.
|
|
表 5 轨迹曲线特征的识别率 Table 5 The recognition rate of trajectory curve |
为了验证本文所用方法的有效性,将其与现有的几种方法进行对比,根据实验结果可知, 文献[2-3, 5-7]使用传统的统计特征用于分类识别,所得到的最高识别准确率为93.87%.而本文使用的轨迹曲线特征用于分类识别,得到的识别率为95.60%,在分类识别率上提高了近2%,说明本文使用的轨迹曲线特征能够有效地用于身份识别,但步态轨迹曲线特征也受到曲线自身的制约.将步态轨迹曲线特征和统计特征进行融合,融合后的特征可以进一步提高人体身份识别率,识别率达到97.10%.
4 结束语基于手机加速度传感器的步态特征身份识别是近几年开始的身份识别方法.一般都是从时、频域提取的统计特征用于分类识别,前人在统计特征值方面的研究已经较为成熟,想要从中提取新的特征值较为困难.与传统的统计特征不同,本文从图像学轨迹形状角度出发,根据步态的轨迹曲线特征来完成身份识别.针对方向角描述子缺乏整体方面的描述以及傅里叶描述子在局部描述中的欠缺,本文将这2种描述子相结合作为一种步态轨迹曲线特征.实验结果表明,相对于单独使用方向角描述子和傅里叶描述子,这是一种更为有效的步态轨迹曲线特征.轨迹曲线特征不同于传统的时域统计特征,本文将二者相结合取得了较高的识别率.同时本文也存在一些问题,如仅考虑了正常步行时的步态曲线,存在局限性.下一步需要对跑、上、下楼梯等多种情形下的步态曲线分析,同时也需要考虑手机放置对识别率的影响.
| [1] |
KWAPISZ J R, WEISS G M, MOORE S A. Cell phone-based biometric identification[C]// IEEE International Conference on Biometrics: Theory Applications and Systems. Washington, 2010: 1-7.
(  0) 0) |
| [2] |
PRIMO A, PHOHA V, KUMAR R, et al. Context-aware active authentication using smart phone accelerometer measurements[C]// IEEE Conference on Computer Vision and Pattern Recognition Workshops. Columbus, 2014: 98-105.
(  0) 0) |
| [3] |
WATANABE Y. Influence of holding smart phone for acceleration-based gait authentication[C]//Fifth International Conference on Emerging Security Technologies. Alcala de Henares, 2014: 30-33.
(  0) 0) |
| [4] |
HOANG T. Adaptive cross-device gait recognition using a mobile accelerometer[J]. Journal of information processing systems, 2013, 9(2): 333-348. DOI:10.3745/JIPS.2013.9.2.333 (  0) 0) |
| [5] |
HOANG T, CHOI D. Secure and privacy enhanced gait authentication on smart phone[J]. Scientific world journal, 2014(3): 438254. (  0) 0) |
| [6] |
HOANG T, CHOI D, VO V, et al. A lightweight gait authentication on mobile phone regardless of installation error[M]. Berlin: Springer, 2013, 83-101.
(  0) 0) |
| [7] |
刘雅坤. 基于运动信息的步态模式与步态变换研究[D]. 沈阳: 东北大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10145-1016005147.htm
(  0) 0) |
| [8] |
LIU P, LI X, LIU W, et al. Fourier-based multi-scale representation and progressive transmission of cartographic curves on the internet[J]. Cartography and geographic information Science, 2015, 1-15. (  0) 0) |
| [9] |
BOUBAKER H, TAGOUGUI N, ABED H E, et al. Graphemes segmentation for arabic online handwriting modeling[J]. Journal of information processing systems, 2014, 10(4): 503-522. DOI:10.3745/JIPS.02.0006 (  0) 0) |
| [10] |
王凯, 孙咏梅, 张泓, 等. 体域网中基于特征组合的步态行为识别[J]. 中国科学(信息科学), 2013, 43(10): 1353-1364. (  0) 0) |
| [11] |
王杰, 程学新, 彭金柱. 一种基于粒子群算法优化的加权随机森林模型[J]. 郑州大学学报(理学版), 2018, 52(1): 72-76. (  0) 0) |
| [12] |
SUN B, WANG Y, BANDA J. Gait characteristic analysis and identification based on the iPhone′s accelerometer and gyrometer[J]. Sensors, 2014, 14(9): 17037. DOI:10.3390/s140917037 (  0) 0) |
| [13] |
LIU B. A study of personalized recommendation evaluation based on customer satisfaction in e-commerce[C]// International Conference on Computer Science and Service System. Nanjing, 2011: 129-132.
(  0) 0) |
| [14] |
YOUN I H, CHOI S, MAY R L, et al. New gait metrics for biometric authentication using a 3-axis acceleration[C]// Consumer Communications and Networking Conference. Las Vegas, 2014: 596-601.
(  0) 0) |
 2018, Vol. 50
2018, Vol. 50


