2. 桂林电子科技大学 机电工程学院 广西 桂林 541004
2. College of Mechanical and Electrical Engineering, Guilin University of Electronic Technology, Guilin 541004, China
水泥路面具有造价相对低廉、建造周期短等优势,在我国公路中占有较大的比重.为了增加摩擦,在建造水泥路面时,都需要增加刻槽.由于路面刻槽在图像上的灰度值与裂缝极其相似,因而刻槽的存在使得裂缝的提取变得异常困难.由于刻槽的存在,路面经过长时间的磨损,使得刻槽中存在大量的污染物,这些污染物也导致了刻槽间的灰度值具有较大差异,这也增加了裂缝提取的难度.对于裂缝识别而言,图像分割是裂缝自动检测至关重要的一步[1].文献[2]使用二维小波变换对高频水平子图中的刻槽进行抑制,但同时弱化了横向裂缝;随着图像技术的发展,频域处理也越来越频繁.文献[3]利用二维傅里叶变换(FFT)消除刻槽,并使用同态滤波增强裂缝对比度,同时采用自适应方向的LoG算法在空域中增强裂缝.文献[4]将离散傅里叶变换应用在异步电机参数辨识中.文献[5]采用了方向增强的LoG在抑制刻槽的同时也存在弱化横向裂缝的问题.文献[6]使用分块直方图均衡的方法,该方法在方块边界处易引入新的噪声,不利于后续裂缝的提取.
本文针对在水泥刻槽路面图像识别裂缝中存在刻槽等噪声干扰,利用频域进行降噪以去除刻槽对裂缝识别的影响.首先,通过频域滤波降低图像中刻槽对后续处理的影响.滤波后运用动态最短路径将图像中疑似裂缝的区块挑选出来,经过后续二值化、裂缝拼接等处理,最后得到裂缝图像.实验结果表明,该方法可以很好地去除刻槽、准确地识别裂缝.
1 水泥路面图像的频域滤波由于水泥路面刻槽在空域图像中呈现出一定的周期性,利用刻槽的周期性,在频域内消除或抑制它是非常典型的条纹去除方法[7].如图 1所示:从水泥路面图中可以看出刻槽相对成水平分布,且刻槽间的间距大致相等.利用这个特征,将路面图像结果经傅里叶变换转换到频率域后,使用特有的滤波器去除刻槽对裂缝识别的影响.

|
图 1 水泥路面图1 Figure 1 Cement pavement 1 |
对尺寸为M*N的图像函数f(x, y)进行离散傅里叶变换:
| $ F\left( {u, v} \right) = \frac{1}{{MN}}\sum\limits_{x = 0}^{M-1} {\sum\limits_{y = 0}^{N-1} {f\left( {x, y} \right){{\rm{e}}^{-j2{\rm{ \mathsf{ π} }}\left( {\frac{{ux}}{M} + \frac{{vy}}{N}} \right)}}} } . $ | (1) |
同样,给出F(u,v),也可以通过傅里叶反变换获得f(x, y), 表达式如下:
| $ f\left( {x, y} \right) = \sum\limits_{x = 0}^{M-1} {\sum\limits_{y = 0}^{N-1} {F\left( {u, v} \right){{\rm{e}}^{-j2{\rm{ \mathsf{ π} }}\left( {\frac{{ux}}{M} + \frac{{vy}}{N}} \right)}}} } . $ | (2) |
在频率域滤波时,往往要用(-1)x+y乘以f(x, y)将F(u,v)原点变换到频率坐标下的(M/2, N/2),即傅里叶变换的原点被设置在u=M/2和v=N/2上.图 2为图 1经过傅里叶变换后的功率谱图像.

|
图 2 功率谱图 Figure 2 Power spectrum diagram |
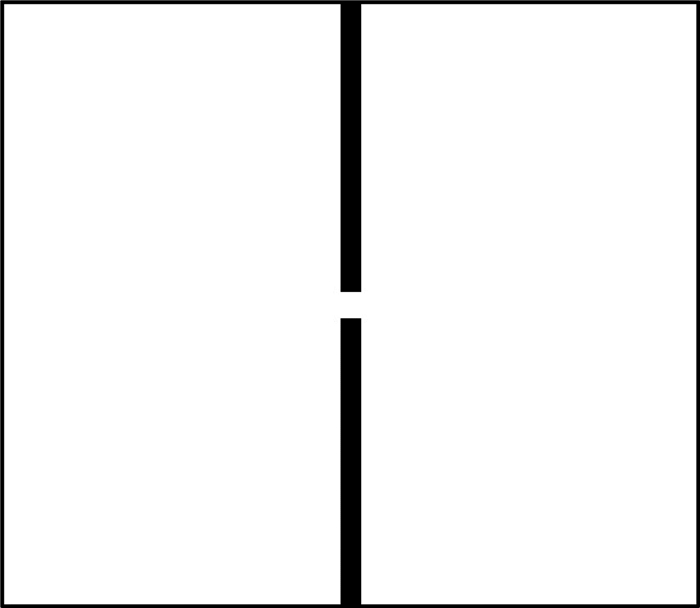
从功率谱图像可以看出,除图像中心外,在y轴上有一些等距的亮斑,这些亮斑在空间域中对应的就是图像中的刻槽.观察不难发现这些亮斑均在y轴附近,故可设计一种滤波器,除中心原点附近的y轴附近,其他y轴附近的滤波器数值均为0(为了便于观看给图像加上了边框,如图 3所示).其数学表达为
|
图 3 带阻滤波器 Figure 3 Band elimination filter |
| $ H\left( {u, v} \right) = \left\{ \begin{array}{l} 0\frac{M}{2}-a < u < \frac{M}{2} + a, \left| {v-\frac{N}{2}} \right| > b, \\ 1, \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots 其他. \end{array} \right. $ | (3) |
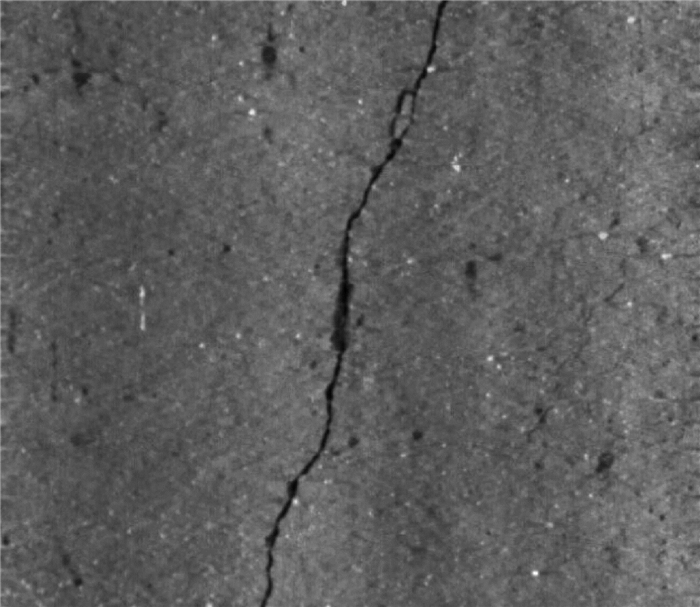
使用传递函数H(u, v)的滤波器对F(u,v)进行滤波,然后将滤波后的函数进行傅里叶反变换,得到无刻槽的路面图像(如图 4),原水泥刻槽路面图像中的刻槽去除了,而保存的裂缝还是相当不错的.当裂缝和刻槽平行时(如图 5)傅里叶滤波的效果如图 6所示.从图中可以看出当裂缝与刻槽平行时,滤波后在刻槽去除的同时裂缝也有一定程度的衰减.这也是本文刻槽滤波需要改进的地方.
|
图 4 滤波后的图像1 Figure 4 Filtered image 1 |

|
图 5 水泥路面图2 Figure 5 Cement pavement 2 |

|
图 6 滤波后的图像2 Figure 6 Filtered image 2 |
考虑到路面图像分辨率一般较大,求取动态最短路径时所需的时间较长,且摄像机在拍摄路面图像存在光照不均等问题[8].故将路面图像分割成多个不重叠的小方块.在路面图像的划分中,方块不能太小或太大,太小会使得在使用动态最短路径时,噪声对最短路径的结果影响较大,从而影响提取效果;划分方格太大,会使运算程度复杂,消耗时间较长.经过大量实验证明,当图像划分为16*16的方块时,其运算时间与效果较好.故本文采用的方块大小为16*16.
从方格内像素的灰度值看出是其邻域到其的距离,可以看成是求解动态最短路径问题.如图 7.

|
图 7 方格像素路径距离表 Figure 7 Square pixels path distance table |
其中A点为路径起始点,B点为路径终止点.(x, y)为像素坐标,f(x, y)为像素的灰度值,这里代表该点到其邻域点距离.如点(6, 6) 到点(6, 7) 的距离为f(6, 7).为了便于观察,将其点进行编号,像素点依次由左向右、由上到下进行编号,编号为0到255.
定义s(x, y)为点x到点y的距离,令:
A点到x(即点(0, x))的距离为s(A, x)=f(0, x), x=0, 1, 2,…,15;
A点到16*x(即点(x, 0))的距离为s(A, 16*x)=f(x, 0), x=0, 1, 2,…,15;
A点到16*x+15(即点(x, 15))的距离为s(A, 16*x+15)=f(x, 15), x=0, 1, 2,…,15;
15*16+x(即点(15, x))到B点的距离为s(15*16+x, B)=0, x=0, 1, 2,…,15;
16*x(即点(x, 0))到B点的距离为s(16*x, B)=0, x=0, 1, 2,…,15;
16*x+15(即点(x, 15))到B点的距离为s(16*x+15, B)=0, x=0, 1, 2,…,15.
定义S(x)为点A到点x的最小动态距离,其初始值S(x)=f(x/16, x%16).其动态最短距离的定义为:
S(x)=min({S((x/16+m)*16+x%16+n)*P[(x/16+m)*16+x%16+n]+
f(x/16, x%16)}/(P[(x/16+m)*16+x%16+n]+1)),
其中:P[k]为点A到点k所需的步骤数,m=-1,0,1;n=-1,0,1;且x/16+i≥0,x%16+j≥0(x/16为x对16取正,x%16为x对16取余).
A点到B点的距离定义为S=min(S(x)), 其中:x/16=15或x%16=0或x%16=15且P[x]>5.
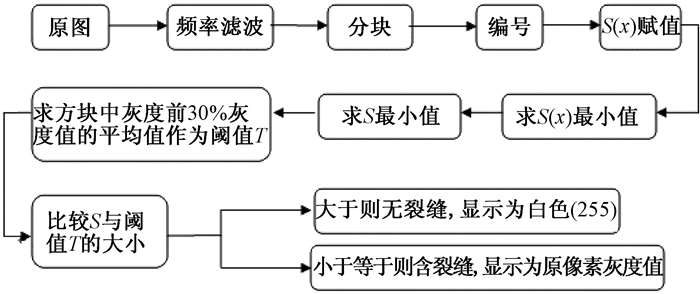
由于在含裂缝的方块中,裂缝一般的平均宽度不超过4个像素,故裂缝所占比例不会超过(16*4)/(16*16), 即25%.考虑到路面噪音的影响,故取其灰度值较低的30%的平均值作为阈值,提取裂缝方块.设置P[x]的阈值是为了防止方格边境像素灰度值较低(如受到噪音的影响),从而影响整个动态求取最短距离的结果,造成识别结果误检率较高.图 8为裂缝方格操作流程图.
|
图 8 操作流程图 Figure 8 Operation flow chart |
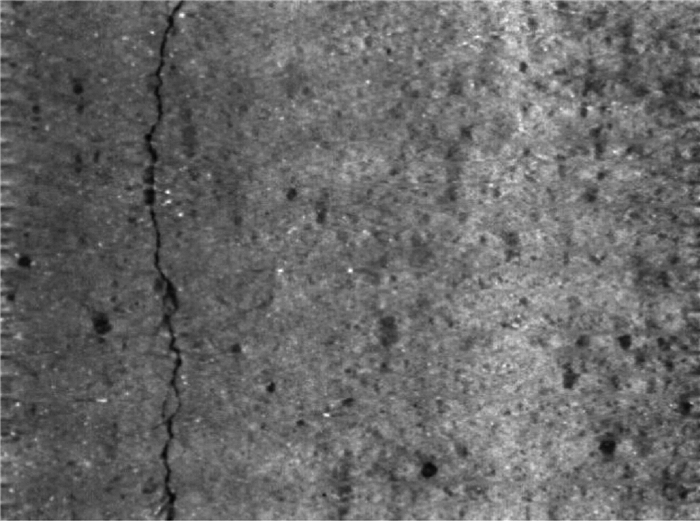
图 9~12为在不同P[x]阈值下裂缝方格的提取状况, 可以看出当P[x]为3时,所提取的裂缝方格中存在较多的误检,而当P[x]为8时,提取的裂缝方格误检较少,但存在较为严重的漏检的现象,这也是我们不愿看见的情形.综合考虑后,当P[x]为5时,误检和漏检的情况相对较少,提取的裂缝方格相对最优.经过大量实验对比发现,当P[x]阈值为5时,其动态最短路径算子的识别率相对较好.
|
图 9 滤波后的图像3 Figure 9 Filtered image 3 |

|
图 10 P[x]阈值为3的识别图 Figure 10 Recognition of threshold P[x] to 3 |

|
图 11 P[x]阈值为5的识别图 Figure 11 Recognition of threshold P[x] to 5 |

|
图 12 P[x]阈值为8的识别图 Figure 12 Recognition of threshold P[x] to 8 |
图 13为频率滤波后,使用上述本节所使用的动态最短路径算子对裂缝这种“线状”目标进行识别的效果图.该算子已经将滤波后图像中的裂缝方块识别出来,当然其中也存在误检和漏检的情况.从图中可以看出,误检的裂缝方块相对离散,方块相对“孤立”,运用这一特性可以将误检的裂缝方块去除,图 14为离散方块去除图,可以看出绝大多数“孤立”的方块已经被去除,这为进一步的提取裂缝提供较好的基础.

|
图 13 动态最短路径裂缝识别图 Figure 13 Dynamic shortest path fracture identification |

|
图 14 离散方块去除图 Figure 14 Discrete blocks removal |
将频率滤波后的图像进行5*5的高斯滤波,目的是给图像减噪,利于最后的裂缝提取.将频率域滤波后的图像进行高斯滤波,然后对图像进行自适应阈值处理(图 15).图 16为将自适应阈值图与离散方块去除图相交得到的自适应裂缝方块图.

|
图 15 自适应阈值操作后图像 Figure 15 Adaptive threshold operation |

|
图 16 自适应裂缝方块图 Figure 16 Adaptive crack square |
经过上述处理后的图像变为了二值图像,原图中绝大多数裂缝噪音已经被去除.从图 16中可以看到,在含有裂缝的方块中还存在一些离散的小“颗粒”,这些较小的“颗粒”很明显不是我们所需要的.接下来对自适应裂缝方块图像进行颗粒的筛除.裂缝提取过程中,由于频率滤波后的图像存在与裂缝灰度值相近的杂点,在提取裂缝的同时还应将这些杂点去掉.由于这些颗粒毫无规律,且相对独立,因此可以通过其连通域的面积、长短轴等特征[9]将“颗粒去除”.根据经验,设定面积最小阈值为10,长短轴比值最大阈值为0.9,去除路面污点[10].通过实验验证,对颗粒的面积与长短轴按照上述阈值设置对颗粒杂点去除的效果相对较好.颗粒去除后,此时得到若干不连续的裂缝片段图像,如图 17所示.裂缝片段拼接历来都是裂缝图像识别的难点,通常使用几何法、方格法、形态学法[11].本文采用的是先提取裂缝片段端点,根据裂缝片段端点之间的距离与裂缝端点的延伸方向等因素,选取最优的端点与之连接,实现裂缝片段的拼接.如图 18.

|
图 17 颗粒去除图 Figure 17 Particle removal |

|
图 18 裂缝片段连接图 Figure 18 Crack segment connection |
为了验证算法的效果,选用了200幅水泥刻槽裂缝图像进行识别,验算其正确性,通过实验验证该算法的裂缝识别准确率达到92%.图 19选取了一种典型的水泥路面裂缝作为说明.从图中可以看出,主要裂缝都可被识别.对于较细的裂缝,由于本文采用的是自适应二值化导致较细裂纹在二值图中断断续续,而在过滤“颗粒”噪声时,容易将较细的裂纹过滤掉,从而导致细裂纹提取不完整.这也是下一步有待研究的内容.图 19(a)、(d)为垂直裂缝与倾斜裂缝原图;(b)、(e)为利用动态最短路径识别裂缝方块的识别图;(c)、(f)为最终识别效果图.从图 19(b)可以看出当图像污染较多时,用动态最短路径识别裂缝方块,提取的结果中噪音模块较多.当图像污染较少时,通过该方法识别裂缝方块的准确率较高.

|
图 19 试验结果图 Figure 19 Test results |
1) 提出了基于动态最短路径的水泥混凝土路面裂缝识别方法,由频域滤波、动态最短路径提取裂缝方块、裂缝片段提取和裂缝片段拼接4个主要步骤实现.
2) 频域滤波是通过傅里叶变换使用带阻滤波器来实现抑制刻槽.
3) 在空域图像中,裂缝成“线状”分布,利用动态最短路径可以求出各个方块中的最短距离,通过与其方块内像素灰度值较小的30%灰度平均值进行比较,来实现裂缝方块的提取.
4) 针对裂缝不连续的问题,先提取裂缝片段端点,根据裂缝片段端点之间的距离与裂缝端点的延伸方向等因素,选取最优的端点与之连接后,将裂缝片段拼接起来,实现裂缝的提取.
| [1] |
TSAI Y C, KAUL V, MERSEREAU R. Critical assessment of pavement distress segmentation methods[J]. Journal of transportation engineering, 2010, 136(1): 11-19. DOI:10.1061/(ASCE)TE.1943-5436.0000051 (  0) 0) |
| [2] |
潘玉利, 赵怀志. 基于二维傅里叶变换的水泥路面图像刻槽去除的方法: 101419668A[P]. 2009.
(  0) 0) |
| [3] |
英红, 罗宏伟, 谈至明, 等. 基于消除刻槽的水泥路面新生裂缝识别方法[J]. 同济大学学报(自然科学版), 2013, 41(1): 78-82. (  0) 0) |
| [4] |
任志斌, 曾彪, 曾德墙. 运用离散傅里叶变换在异步电机参数辨识中的应用[J]. 河南科技大学学报(自然科学版), 2014, 35(3): 58-63. (  0) 0) |
| [5] |
关斌. 一种改进的自适应各向异性LoG算子[J]. 科学技术与工程, 2010, 10(12): 2992-2996. DOI:10.3969/j.issn.1671-1815.2010.12.044 (  0) 0) |
| [6] |
肖靖. 道路裂缝识别算法研究[D]. 北京: 北京邮电大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10013-2009231391.htm
(  0) 0) |
| [7] |
张宏, 英红. 频域滤波的水泥路面图像降噪增强方法[J]. 土木建筑与环境工程, 2015, 37(3): 48-52. (  0) 0) |
| [8] |
李莉, 陈长, 孙立军. 改进的路面图像背景校正算法[J]. 同济大学学报(自然科学版), 2011, 39(1): 79-84. (  0) 0) |
| [9] |
刘凡凡, 徐国爱, 肖靖, 等. 基于连通域相关及Hough变换的公路路面裂缝提取[J]. 北京邮电大学学报, 2009, 32(2): 24-28. (  0) 0) |
| [10] |
荣婧, 潘玉利. 基于图像的水泥路面裂缝识别方法及应用[J]. 北京邮电大学学报, 2012, 35(6): 121-124. (  0) 0) |
| [11] |
SUN Y, SALARI E, CHOU E. Automated pavement distress detection using advanced image processing techniques[C]//Proceedings of IEEE International Conference on Electro / Information Technology. Windsor University, 2009:373-377. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5189645
(  0) 0) |
 2017, Vol. 49
2017, Vol. 49


