郑州大学学报（理学版）  2018, Vol. 50 Issue (3): 39-45  DOI: 10.13705/j.issn.1671-6841.2017211

引用本文  

袁巩生, 王丽珍, 陈红梅, 等. 基于模式融合挖掘巨型频繁co-location模式[J]. 郑州大学学报(理学版), 2018, 50(3): 39-45.
YUAN Gongsheng, WANG Lizhen, CHEN Hongmei, et al. Mining Spatial Colossal Prevalent Co-location Patterns Based on Pattern Fusion Method[J]. Journal of Zhengzhou University(Natural Science Edition), 2018, 50(3): 39-45.

基金项目

国家自然科学基金项目(61472346，61662086)；云南省自然科学基金项目(2016FA026，2015FB114)

通信作者

王丽珍(1962—)，女，云南丽江人，教授，主要从事空间数据挖掘、计算机算法研究，E-mail:lzhwang2005@126.com

作者简介

袁巩生(1991—)，男，山东曹县人，硕士研究生，主要从事空间数据挖掘研究，E-mail: 732514624@qq.com

文章历史

收稿日期：2017-07-13
Contents              Abstract              Full text              Figures/Tables              PDF
基于模式融合挖掘巨型频繁co-location模式
袁巩生 , 王丽珍 , 陈红梅 , 段江丽     
云南大学 信息学院 云南 昆明 650091
收稿日期：2017-07-13
基金项目：国家自然科学基金项目(61472346，61662086)；云南省自然科学基金项目(2016FA026，2015FB114)
作者简介：袁巩生(1991—)，男，山东曹县人，硕士研究生，主要从事空间数据挖掘研究，E-mail: 732514624@qq.com.
通信作者：王丽珍(1962—)，女，云南丽江人，教授，主要从事空间数据挖掘、计算机算法研究，E-mail:lzhwang2005@126.com.
摘要：利用模式融合思想提出了一个空间co-location模式挖掘算法，该算法通过每次融合小模式来快速生成含有大量特征的巨型频繁模式，从而避开了大量的中间模式.并且，由于模式融合旨在产生近似解，因此又引进了一个质量评估模型，评估算法返回的模式.
关键词：巨型频繁co-location模式挖掘    co-location核模式    模式融合    
Mining Spatial Colossal Prevalent Co-location Patterns Based on Pattern Fusion Method
YUAN Gongsheng , WANG Lizhen , CHEN Hongmei , DUAN Jiangli     
School of Information Science and Engineering, Yunnan University, Kunming 650091, China
Abstract: Based on pattern-fusion method, a novel mining approach to efficiently mine rather large spatial co-location pattern was presented. With pattern-fusion method, rather large pattern was found by fusing its small core patterns in one step, whereas some algorithms had to examine a large number of mid-sized patterns. Since the pattern fusion aimed at getting a good approximation to the complete set of the rather larger co-location pattern, a quality evaluation model to evaluate the result set was introduced.
Key words: spatial colossal prevalent co-location pattern mining    spatial co-location core pattern    pattern fusion    
0 引言

Apriori[1]是经典的挖掘频繁项集的算法，经典的Join-based[2]、Join-less[3]等co-location挖掘算法便是类Apriori算法，它们通过利用先验原理，能够有效挖掘出所有的频繁co-location模式.然而，根据频繁模式的定义，频繁模式的任何子集都是频繁的，那么最终可能挖掘出大量的模式.为了解决这一问题，研究者提出了挖掘TOP-k闭模式[4]等算法，但取得的效果却是有限的.更重要的是，在现实生活中，用户更在意的是从一堆数据中能发现什么样的大模式(尽可能多的含有空间特征).例如对于一个生态系统来说，若系统的结构越复杂，包含的物种越多(大模式)，该系统抵抗外界干扰的能力就越强.相反，结构越简单，那么它的抗干扰能力就越弱，越容易受外界的影响.因此，大模式在判断某个生态系统的稳定性和地区植被分布的多样性等方面有着极其重要的意义.

当需要处理的数据集不仅拥有较大的规模，而且可能包含大量的结果模式集时，为了得到结果集中那些为数不多的巨型模式，就必须找出所有的频繁模式.也就是说，这将浪费大量的时间来生成中间模式.因为现有的算法大都是依据先验原理，通过深度或广度优先遍历的策略遍历整个搜索空间，从而验证每个候选模式是否是频繁的.而在传统事务数据的挖掘中，已经有人提出了挖掘长模式的算法[5-6]，且正沿着两个方向探索：方向一是深化利用垂直数据格式，扩充模式增长的方法，处理具有大量项，但只有少量元组的数据集; 方向二就是本文所借鉴的模式融合[7]思想.

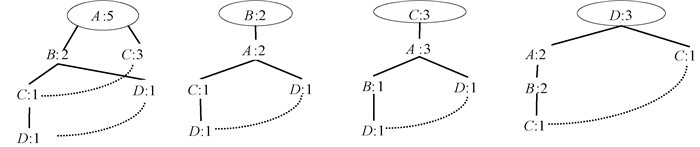
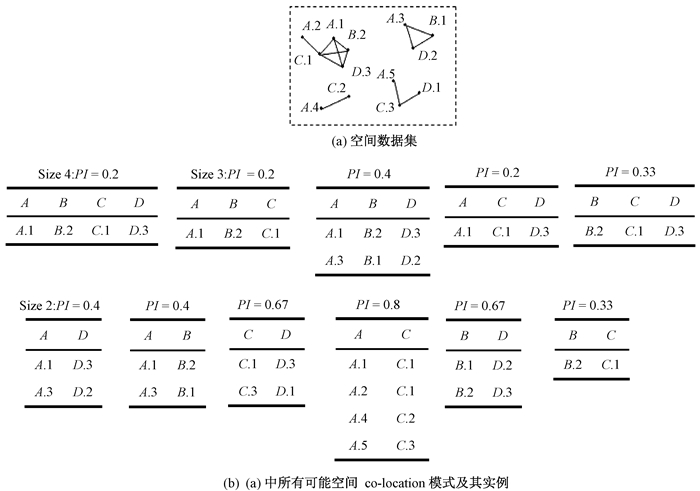
1 相关定义

空间特征代表了空间中不同种类的事物.实例表示的是一个具体空间位置上的对象，每个实例拥有一个唯一的编号，如图 1(a)中A.1.若两个实例满足空间邻近关系R，当且仅当它们之间的欧氏距离小于等于给定的阈值d(d>0)，而对于满足R关系的两个实例，我们用一条线段连接它们，如图 1(a)中A.1和B.2.团是任意两个不同特征的实例之间都满足R关系的实例集，图 1(a)中{A.1, B.2, C.1, D.3}便是一个团.倘若一个团包含了co-location模式c中的所有特征，且此团中没有任何一个真子集可以包含c中的所有特征，那么它就是c的一个行实例，记为row-instance(c).而c的所有行实例的集合称为表实例，记为table-instance(c).我们使用参与率和参与度的大小来度量模式的频繁性，且参与率和参与度随着co-location模式阶的增大单调递减[8].

图 1 空间特征和空间实例 Figure 1 Spatial features and spatial instances

定义1   与阶数较小的模式相比，我们发现阶数较大的空间co-location模式常常携带更重要的信息，称这种空间co-location模式为巨型co-location模式.

在给出具体空间co-location模式的模式距离之前，我们先设Ec(f)=πf(table_instance(c))，它表示空间co-location模式c的表实例中所含的特征f(f∈c)的不同实例个数.

定义2  给定两个co-location模式c和c′，设f为模式c和c′的共有空间特征，也就是说，f∈c∩c′，那么关于模式c和c′的共有空间特征f的特征距离[9]被定义为：

$ F{D_f}\left( {c, c\prime } \right) = 1 - \frac{{|{E_c}\left( f \right) \cap {E_{c\prime }}\left( f \right)|}}{{|{E_c}\left( f \right) \cup {E_{c\prime }}\left( f \right)|}}. $ (1)

定义3   给定空间co-location模式c和c′，那么c和c′的模式距离[9]定义为：

$ D\left( {c, c\prime } \right) = \left\{ \begin{array}{l} \mathop {{\rm{max}}}\limits_{\forall f \in c \cap c\prime } F{D_f}\left( {c, c\prime } \right), \;\;\;\;{\rm{if}}\;\;c \cap c\prime \ne \emptyset \\ 1, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{otherwise}} \end{array} \right.. $ (2)

定义4  对于空间co-location模式c，模式$c\prime \subseteq c $称为c的τ-空间co-location核模式，简称为空间核模式，当且仅当$ \mathop {{\rm{max}}}\limits_{\forall f \in c \cap c\prime } \frac{{{E_c}\left( f \right)}}{{{E_{c\prime }}\left( f \right)}} \ge \tau , 0 < \tau \le 1$，其中τ称为核比率.

对于一个空间co-location模式c，将其所有空间co-location核模式的集合记为Cc.

定义5  若空间co-location模式c关于τ是d鲁棒的(记做(d, τ)-鲁棒的)，当且仅当从c中删除d个空间特征后，结果模式仍然是c的τ-空间核模式.即$d = \mathop {{\rm{max}}}\limits_{c\prime } \{ |c| - |c\prime ||c\prime \subseteq c $, 并且c′是c的τ-空间核模式}.

定理1   若c′∈Cc，f∈c，那么c′∪f∈Cc.

证明  因为$\mathop {{\rm{max}}}\limits_{\forall f \in c \cap \left( {c\prime \cup f} \right)} \frac{{{E_c}\left( f \right)}}{{{E_{c\prime \cup f}}\left( f \right)}} \ge \mathop {{\rm{max}}}\limits_{\forall f \in c \cap c\prime } \frac{{{E_c}\left( f \right)}}{{{E_{c\prime }}\left( f \right)}} \ge \tau , $所以，c′∪f∈Cc.

定理2  对于满足(d, τ)-鲁棒的空间co-location模式c，|Cc|≥2d.

证明  见文献[7].

由于鲁棒性的存在，巨型co-location模式往往会含有大量的空间核模式.又因为巨型模式与它对应的空间核模式之间的鲁棒性关系可扩展多层，这样便有了空间co-location核后代的概念.

定义6   对于给定的co-location模式c和c′，若存在一个序列ci，1≤i≤k，k≥1使对于所有的0≤i≤k，都能让c=c0，c′=ck和ci∈Cci+1满足，则c是c′的空间co-location核后代，简称为空间核后代.

2 基于模式融合思想的挖掘算法与算法评估模型

模式融合方法首先生成一个具有较小阶数的频繁co-location模式的完全集.若它包含的模式的数量大于K个，就从集合中随机挑选出K个，否则就返回这K个模式作为结果集交给用户.根据定义可知，对于随机选取到的K模式中每个模式c来说，它很可能是某个巨型模式c′的空间核后代.那么，在这K个模式中，先识别出c′的所有空间核后代，再一一合并它们.通过此方式将会产生c′的更长的空间核后代，这使算法在生成c′的过程中可跳跃前进.以此类推，通过每次在产生较长的空间核后代的集合中再选择K个模式作为初始池，用于下次迭代.

从给出的方法中可以看出，需要先识别出c′的所有空间核后代，然后才能合并它们.接下来将探讨当随机选取到c′的一个空间核后代c后，该如何找出c′的其他空间核后代.

定理3   如果两个空间co-location模式c，c′∈Cα，那么D(c, c′)≤r(τ)，其中，$r\left( \tau \right) = 1 - \frac{1}{{2/\tau - 1}} $.

证明   因为c，c′∈Cα，所以根据空间co-location模式的特征距离，可得

$ \frac{{{\rm{|}}{E_c}\left( f \right) \cap {E_{c\prime }}\left( f \right){\rm{|}}}}{{{\rm{|}}{E_c}\left( f \right) \cup {E_{c\prime }}\left( f \right){\rm{|}}}} \ge \frac{{{\rm{|}}{E_\alpha }\left( f \right){\rm{|}}}}{{{\rm{|}}{E_c}\left( f \right) \cup {E_{c\prime }}\left( f \right){\rm{|}}}} = \frac{{{\rm{|}}{E_\alpha }\left( f \right){\rm{|}}}}{{{\rm{|}}{E_c}\left( f \right) + {E_{c\prime }}\left( f \right) - {E_c}\left( f \right) \cap {E_{c\prime }}\left( f \right){\rm{|}}}}. $

根据空间核模式的定义知$\mathop {{\rm{max}}}\limits_{\forall f \in \alpha \cap c} \frac{{{E_\alpha }\left( f \right)}}{{{E_c}\left( f \right)}} \ge \tau , \mathop {{\rm{max}}}\limits_{\forall f \in \alpha \cap c\prime } \frac{{{E_\alpha }\left( f \right)}}{{{E_{c\prime }}\left( f \right)}} \ge \tau $，所以

$ \begin{array}{l} \frac{{{\rm{|}}{E_\alpha }\left( f \right){\rm{|}}}}{{{\rm{|}}{E_c}\left( f \right) + {E_{c\prime }}\left( f \right) - {E_c}\left( f \right) \cap {E_{c\prime }}\left( f \right){\rm{|}}}} \ge \frac{{{\rm{|}}{E_\alpha }\left( f \right){\rm{|}}}}{{{\rm{|}}{E_\alpha }\left( f \right)/\tau + {E_\alpha }\left( f \right)/\tau - {E_\alpha }\left( f \right){\rm{|}}}} = \frac{1}{{2/\tau - 1}}, \\ D\left( {c, c\prime } \right) = \mathop {{\rm{max}}}\limits_{\forall f \in c \cap c\prime } F{D_f}\left( {c, c\prime } \right) = \mathop {{\rm{max}}}\limits_{\forall f \in c \cap c\prime } (1 - \frac{{|{E_c}\left( f \right) \cap {E_{c\prime }}\left( f \right)|}}{{|{E_c}\left( f \right) \cup {E_{c\prime }}\left( f \right)|}}) \le 1 - \frac{1}{{2/\tau - 1}} = r\left( \tau \right). \end{array} $

通过定理3知道c的所有的空间核模式都将存在于一个直径为r(τ)的球形度量空间中.即，若一个空间核模式c′∈Cc，那么在当前池中可通过范围查询的方式找到池中所有c的空间核模式.但定理3的逆定理是不成立的.也就是说，即使c′∈Cc且D(β, c′)≤r(τ)成立，但并不能确定β∈Cc.

对于空间特征实例f.i∈S(实例集合)，该实例的邻居事务集[3]是一个包含f.i和所有与特征实例f.i具有邻居关系的其他空间特征实例的集合，即NT(f.i)={f.i, g.j∈S|R(f.i, g.j)=true and f≠g}，其中f.i被称为参考示例.表 1给出了图 1(a)中所有实例的邻居事务集.当只考虑邻居事务集中的空间特征，不再具体细化到实例时，就得到了特征邻居事务集[3]，如表 1所示.

表 1 关于图 1(a)中所给数据的邻居事务集和特征邻居事务集 Table 1 Neighborhood transactions and feature neighborhood transactions of the data set in Fig. 1(a)

另外，本文使用字典序前缀树结构[4]来存储特征邻近事务集.该结构的优点在于，当需要判断通过模式融合生成的候选模式c是否拥有完整的团关系时，可以提前删除那些不会频繁的候选模式，从而起到剪枝作用.例如图 2给出了表 1中特征邻近事务集的字典序前缀树.在前缀树中，所有的子节点都与根节点具有邻近关系.通过前缀树可得到c的候选星型模式c′，还可得到c′中每个特征的上界参与率，从而得到c的上界参与度值.根据上界参与度值的大小，就可以进行剪枝了.

图 2 关于图 1(a)中数据集的字典序前缀树 Figure 2 Lexicographic prefix-tree of features of the data set in Fig. 1(a)

给定一个n阶巨型co-location模式c和一个包含了c所有k阶子模式的选取池，那么由下面的定理4就可知道, 从这个选取池中随机选取多少个模式才能在一个高概率下覆盖住c.

定理4[7]   当均匀地随机选取m*=(en ln n)个模式的时候，就能在至少1-1/n2概率下覆盖住c中所有的空间特征.

证明   见文献[7].

定义7   对于一个空间co-location模式c，集合S $ \subseteq $ Cc\{c}是c的空间co-location核模式互补集当且仅当 $\mathop \cup \limits_{c\prime \in S} c\prime = c $ ，并记c的所有空间核模式互补集为Γc.

若集合S是c的一个空间核模式互补集，且其出现在挖掘算法的迭代过程中，倘若S中的任一模式被抽选到，那么S中的其他空间核模式很可能将会在“球形”空间被找到.那么通过融合S中的模式便能生成c.所以集合Γc越大，那么生成c的可能性也就越大.而由定理2得出的引理1将给出模式的鲁棒性与Γc的大小有着极其密切的关联.

引理1   一个满足(d, τ)-鲁棒性的空间co-location模式c至少拥有2d-1-1个空间核模式互补集，也就是说，|Γc|≥2d-1-1.

这一引理说明，因为巨型模式比低阶模式拥有更强的鲁棒性，所以模式融合方法能够在很高的概率下生成巨型模式.当然，会有一些低阶但却拥有很强鲁棒性的模式被挖掘出来.但是当我们从当前池随机选取K个种子模式开始新一轮的迭代时，这些低阶模式被随机选中的概率也仅为K/|S|，其中S是当前池.即经过多次迭代后，很大概率上低阶模式被淘汰出局.算法过程如下.

输入：

F={f1, f2, …, fn}为空间特征集; min_prev为最小参与度阈值; d为空间邻近距离阈值;

D为空间数据集; τ为核比率; K为挖掘出巨型频繁空间co-location模式的最大数量.

输出：

满足min_prev的巨型频繁co-location模式集S.

变量：

Pk为k阶频繁空间co-location模式集; k为空间co-location的阶(size); N为邻居实例对;

NT为邻居事务集; ENT为特征邻居事务集; InitPool为初始池;

Begin

1 N=find_neighbor_pairs(D, d);

2 (NT, ENT)=gen_neighbor_transactions(N);

3 for i=1 to n      //遍历空间特征

4  Treei=build_prefix-tree(fi, ENT);

5 P1=F; k=2;

6 Pk=gen_prevalent_colocation(Pk-1);

8 InitPool ← Pk;

9 while |InitPool| > K{

10  S ← ${\rm{\phi}} $; TmpInitPool ← $\phi $;

11  for i=1 to K{

12    Randomly draw a seed c from InitPool;

13    TmpInitPool ←c∪ TmpInitPool; }

14  InitPool ←TmpInitPool;

15  for each c∈ InitPool

16   for each c′ ∈ InitPool

17     if D(c, c′)≤ r(τ)

18      c″=c∪ c′ //模式融合生成新模式c″

19      if clique(c″)==ture

20       if calculate_PI(c″) ≥ min_prev

21        then S← S ∪ {c″};

22  InitPool ← S;

23 }

24 return S;

END

此算法主要包含了3个部分.第1~4行是第1部分，对于给定的D和d, 找到所有的邻居实例对.然后，通过分组每个实例的邻居实例对，生成NT.再根据NT生成ENT.接下来就可以基于ENT中每个特征fi的ENT生成fi的前缀树Treei，其中i=1, 2, …, n.

第5~8行是第2部分，生成2阶频繁空间co-location模式完全集作为模式融合的初始池.

第9~23行是第3部分，是用来生成最终的巨型co-location模式集S.第9行用来控制循环，也是算法终止条件，若得到的结果集S(InitPool)中包含的模式数量大于K就继续运行算法的第3部分，直到满足条件为止.第11~13行用来从初始池中随机选取K个模式.第15~21行对目前初始池中的每个模式c进行检测，判断模式c′是否处于c的球形空间.如果成立，就融合c和c′，从而生成新的较长的模式c″，然后通过前缀树判断这个候选模式是否符合团关系，若符合，在第20行中通过NT生成该模式的表实例，进而计算其真实参与度值.若c″的PI值大于等于min_prev，那就把c″添加到S中.其中，在第19行判断c″是否满足团关系使用的是前缀树方法，并通过上界参与率来剪枝掉一些不满足条件的模式，从而提高算法效率.

定义8   空间co-location模式c和c′的编辑距离[7]Edit(c, c′)被定义为

$ Edit\left( {c, c\prime } \right) = |c \cup c\prime | - |c \cap c\prime |. $ (3)

定义9   给定两个co-location模式集合P={c1, c2, …, cm}和Q={c′1, c′2, …, c′n}，将Q按P的内容划分，得到的模式集划分[7]结果记为πQ={Q1, Q2, …, Qm}，并且πQ满足以下3个条件：

1) Q=∪1≤j≤mQj; 2)若i≠j，则Qi∩Qj= $ \emptyset $; 3) Qi={c′|c′∈P, 并且$ Edit\left( {c, c\prime } \right) = \mathop {{\rm{min}}}\limits_{1 \le j \le m} Edit\left( {c, c\prime } \right)$ }.

定义10   将集合P={c1, c2, …, cm}关于集合Q={c′1, c′2, …, c′n}的平均最大近似误差[7]记为Δ(P, πQ)，其具体公式为$ \Delta \left( {P, {\pi _Q}} \right) = \frac{{\sum\limits_{i = 1}^m {{r_i}} }}{m}$，其中$ {r_i} = \mathop {{\rm{max}}}\limits_{c\prime \in {Q_i}} \frac{{Edit\left( {c\prime , {c_i}} \right)}}{{{c_i}}}$.

若给定两个空间co-location模式集合P和Q，其中P指的是通过模式融合思想挖掘到近似集，Q指的是完整的结果集，有了上述3个定义，便可以使用Δ(P, πQ)来评估P和Q之间的近似程度.也就是说，平均最大近似误差值越小，集合P越接近集合Q.

3 实验分析

本实验的软件平台是：MyEclipse Professional 2014，32位的Windows 7操作系统，硬件平台是：Intel(R) Core(TM)2 Duo CPU T6570@2.10 GHz，2G内存联想笔记本.

表 2给出了两个算法的运行时间.从整体而言，随着空间特征数目N的增大，与基于全连接算法相比，基于模式融合的算法运行所需要的时间要少得多.实验所用数据是通过在60×60的空间区域范围内，对于N个空间特征，每个特征随机进行生成0~100个实例得到的，并把min_prev设为0.25，R关系距离阈值设为5，τ设为0.5，K设为4.表 3中实验所用数据是“云南省三江并流”区域植物分布的真实数据.通过表中的数据可以看出，对于同一组数据，在相同距离阈值、不同最小参与率阈值下，模式融合算法比全连接算法运行时间要少很多.

表 2 合成数据上的运行时间 Table 2 Running time about synthesized data

表 3 真实数据上的运行时间 Table 3 Running time about real data

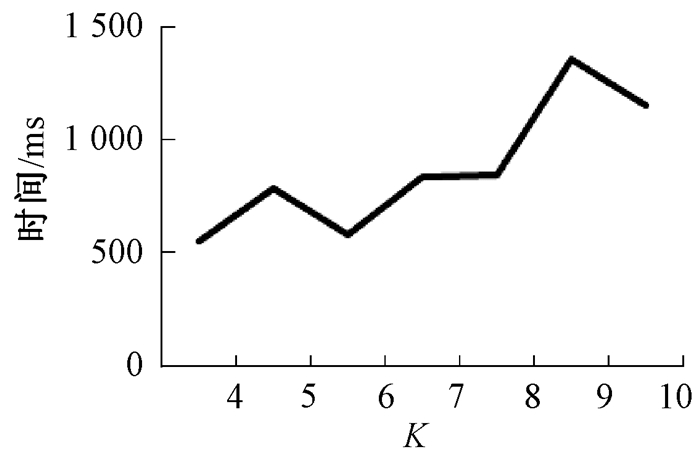
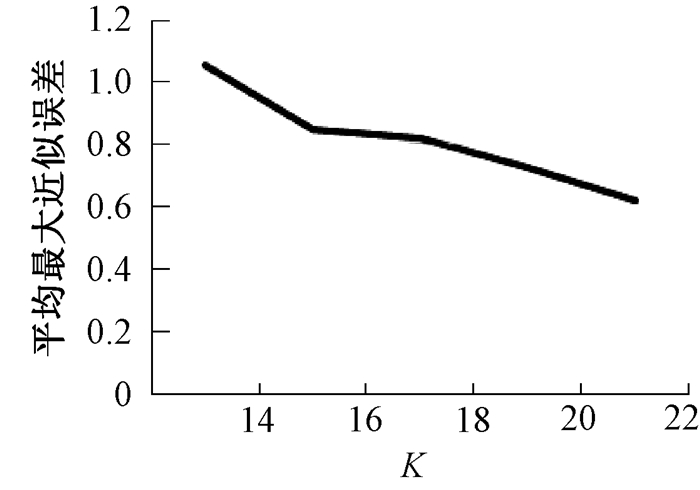
图 3给出当其他参数不变，只增大K值时，对于同一组数据整体而言，基于模式融合策略所提出的模式挖掘算法运行所需时间是逐渐增大的.其中，纵轴的时间单位是ms.图 4给出当其他参数不变，只增大K值的时候，对于同一组数据整体而言，基于模式融合策略所提出的模式挖掘算法挖掘出来的模式质量是逐步提高的.其中，纵轴表示是平均最大近似误差.图 3和图 4实验所用数据都是通过在60×60的空间区域范围内，对于28个空间特征，每个特征随机进行生成0~100个实例得到的，其中min_prev设为0.25，R关系距离阈值设为5，τ设为0.5.

图 3 关于K值变换的算法运行时间 Figure 3 Running time of algorithm about different K

图 4 关于K值变换的平均最大近似误差 Figure 4 Maximum approximation error about different K

之后工作可以先把2阶模式的完全集视为初始池，再进行处理.但是，因模式的数量很多，可能导致时间复杂性不会很低.而且，此方法也会受到随机选取过程的影响，需考虑如何合理地选取空间核模式.另外，还可以尝试模糊思想来挖掘.按照模糊论的知识进行发散思维，看是否能够使用模糊思想来挖掘巨型模式.

参考文献
[1]
AGRAWAL R, LMIELINSKI T, SWAMI A. Mining association rules between sets of items in large databases[C]//ACM SIGMOD International Conference on Management of Data. New York, 1993: 207-216. (0)
[2]
HUANG Y, SHEKHAR S, XIONG H. Discovering co-location patterns from spatial data sets: a general approach[J]. IEEE transactions on knowledge & data engineering, 2004, 16(12): 1472-1485. (0)
[3]
YOO J S, SHEKHAR S. A join-less approach for mining spatial co-location patterns[J]. IEEE transactions on knowledge & data engineering, 2006, 18(10): 1323-1337. (0)
[4]
YOO J S, BOW M. Mining top-k closed co-location patterns[C]//IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services. Fuzhou, 2011: 100-105. (0)
[5]
BAYARDO R J. Efficiently mining long patterns from databases[C]//ACM SIGMOD International Conference on Management of Data. New York, 1998: 85-93. (0)
[6]
AGARWAL R C, AGGARWAL C C, PRASAD V V V. Depth first generation of long patterns[C]// ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, 2000: 108-118. (0)
[7]
ZHU F, YAN X, HAN J, et al. Mining colossal frequent patterns by core pattern fusion[C]//IEEE International Conference on Data Engineering. Istanbul, 2007: 706-715. (0)
[8]
王丽珍, 陈红梅. 空间模式挖掘理论与方法[M]. 北京: 科学出版社, 2014. (0)
[9]
LIU B, CHEN L, LIU C, et al. RCP mining: towards the summarization of spatial co-location patterns[M]. Switzerland: Springer International Publishing, 2015, 451-469. (0)